SOUTH KAZAKHSTAN STATE PEDAGOGICAL INSTITUTE Presentation Theme Elliptic

SOUTH KAZAKHSTAN STATE PEDAGOGICAL INSTITUTE Presentation Theme: Elliptic Paraboloid Student: Ismail Elriza Group: 109 -25

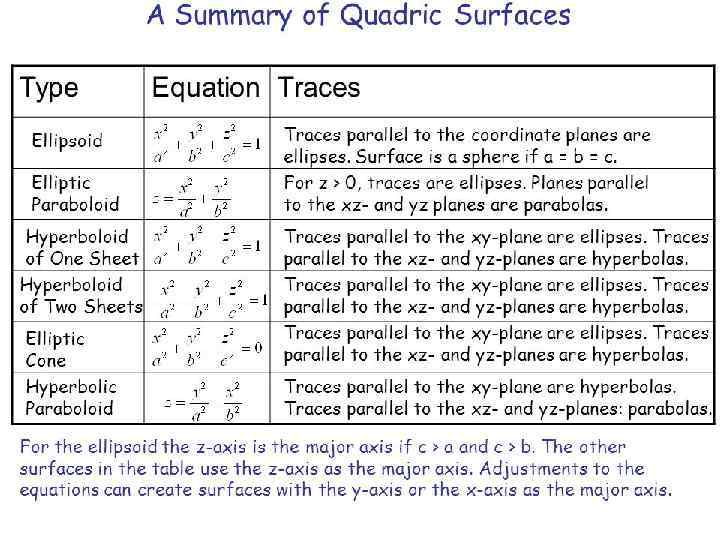
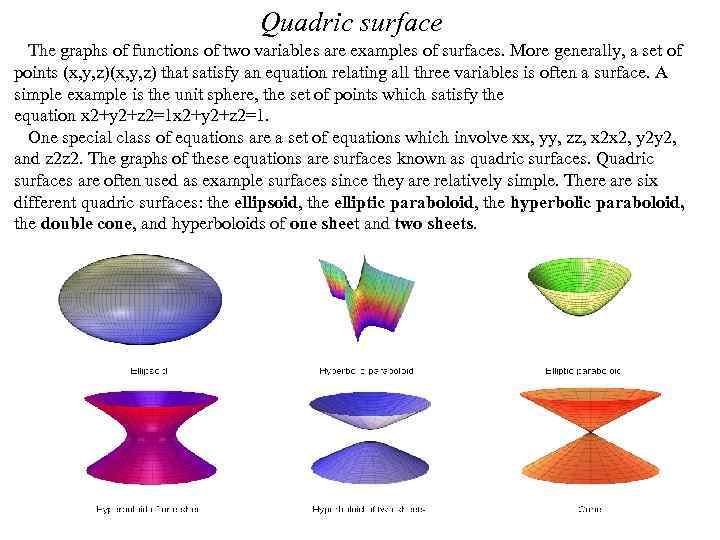Quadric surface The graphs of functions of two variables are examples of surfaces. More generally, a set of points (x, y, z) that satisfy an equation relating all three variables is often a surface. A simple example is the unit sphere, the set of points which satisfy the equation x 2+y 2+z 2=1. One special class of equations are a set of equations which involve xx, yy, zz, x 2 x 2, y 2 y 2, and z 2 z 2. The graphs of these equations are surfaces known as quadric surfaces. Quadric surfaces are often used as example surfaces since they are relatively simple. There are six different quadric surfaces: the ellipsoid, the elliptic paraboloid, the hyperbolic paraboloid, the double cone, and hyperboloids of one sheet and two sheets.

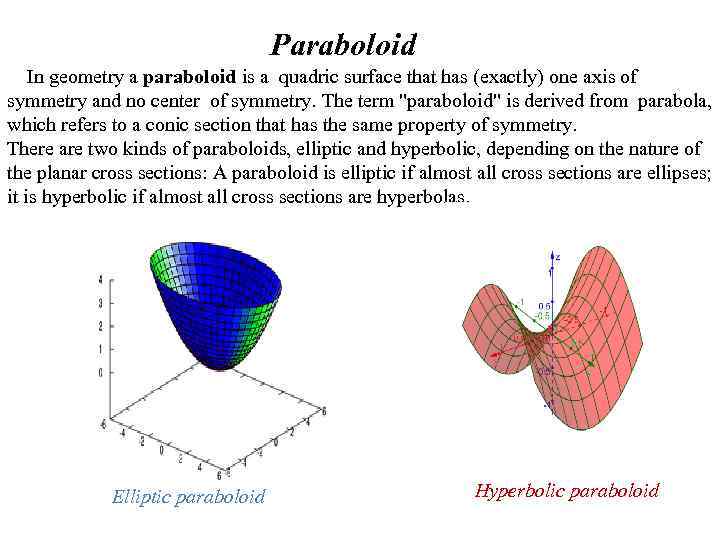Paraboloid In geometry a paraboloid is a quadric surface that has (exactly) one axis of symmetry and no center of symmetry. The term "paraboloid" is derived from parabola, which refers to a conic section that has the same property of symmetry. There are two kinds of paraboloids, elliptic and hyperbolic, depending on the nature of the planar cross sections: A paraboloid is elliptic if almost all cross sections are ellipses; it is hyperbolic if almost all cross sections are hyperbolas. Elliptic paraboloid Hyperbolic paraboloid

With a = b an elliptic paraboloid is a paraboloid of revolution: a surface obtained by revolving a parabola around its axis. It is the shape of the parabolic reflectors used in mirrors, antenna dishes, and the like; and is also the shape of the surface of a rotating liquid, a principle used in liquid mirror telescopes and in making solid telescope mirrors (see rotating furnace). This shape is also called a circular paraboloid. There is a point called the focus (or focal point) on the axis of a circular paraboloid such that, if the paraboloid is a mirror, light from a point source at the focus is reflected into a parallel beam, parallel to the axis of the paraboloid. This also works the other way around: a parallel beam of light incident on the paraboloid parallel to its axis is concentrated at the focal point. This applies also for other waves, hence parabolic antennas

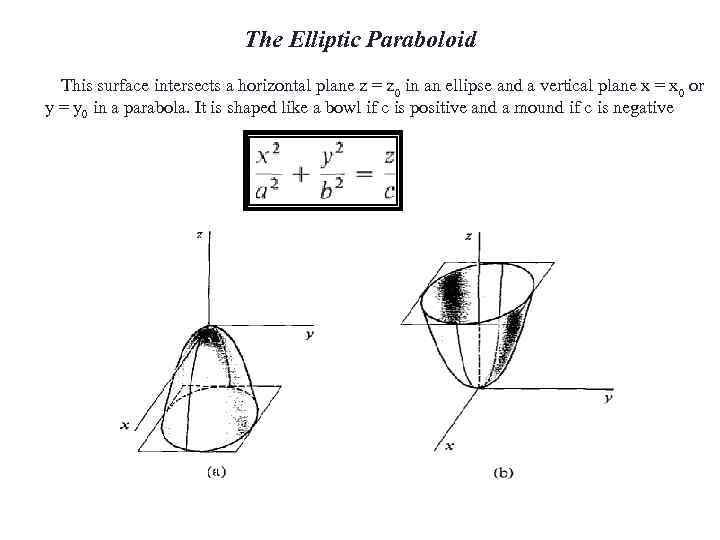The Elliptic Paraboloid This surface intersects a horizontal plane z = z 0 in an ellipse and a vertical plane x = x 0 or y = y 0 in a parabola. It is shaped like a bowl if c is positive and a mound if c is negative

Elliptical paraboloids in the life

The game “Scrabble” P olynomial Write any words. The task is to come up with words that begin with each letter of the word and are relevant to the topic of the lesson Axes Rotation A pex B owl O rdinate L ocus O rigin I ntersection D ouble cone

Conclusion