Составьте уравнение плоскости по 3 точкам 484568

Составьте уравнение плоскости по 3 точкам:

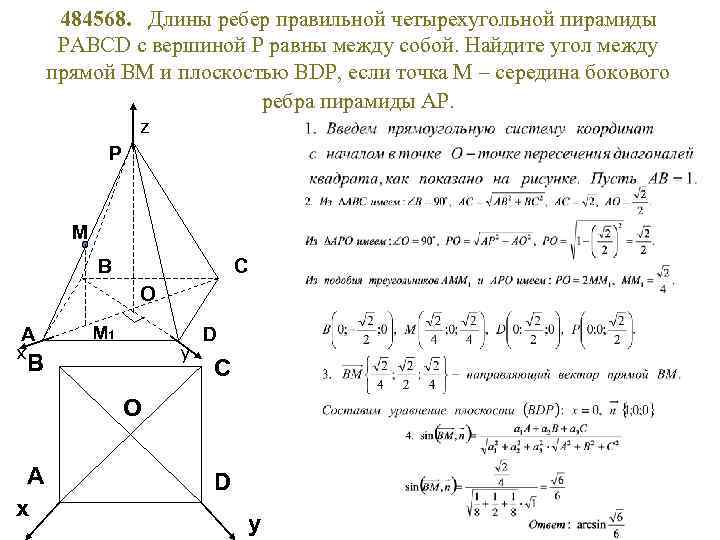484568. Длины ребер правильной четырехугольной пирамиды PABCD с вершиной Р равны между собой. Найдите угол между прямой ВМ и плоскостью BDP, если точка М – середина бокового ребра пирамиды АР. z P M B C O А x М 1 y В D С O А x D y

Задача. Дан куб ABCDA 1 B 1 C 1 D 1 с ребром 1. Точка М-середина ребра АВ, точка К – середина ребра DD 1. Найти угол между плоскостями АКВ 1 и КМС. РЕШЕНИЕ. Введем прямоугольную систему координат, поместив начало координат в точку А. Составим уравнение плоскости АКВ 1. Точка А (0; 0; 0) принадлежит этой плоскости, то d=0. Подставим координаты точек К(0; 1; 0, 5) и В 1 (1; 0; 1) в уравнение плоскости, получим b+c/2=0, a+c=0. Таким образом имеем 2 х+у - 2 z=0. Составим уравнение плоскости КМС. Подставим координаты точек К(0; 1; 0, 5) и М (0, 5; 0; 0), С(1; 1; 0) в уравнение плоскости, получим систему: Уравнение плоскости (КМС) принимает вид 2 х – у +4 z=1. Итак, и угол между плоскостями АВК 1 и КМС находим из

• Расстоянием между скрещивающимися прямыми называется Длина общего перпендикуляра

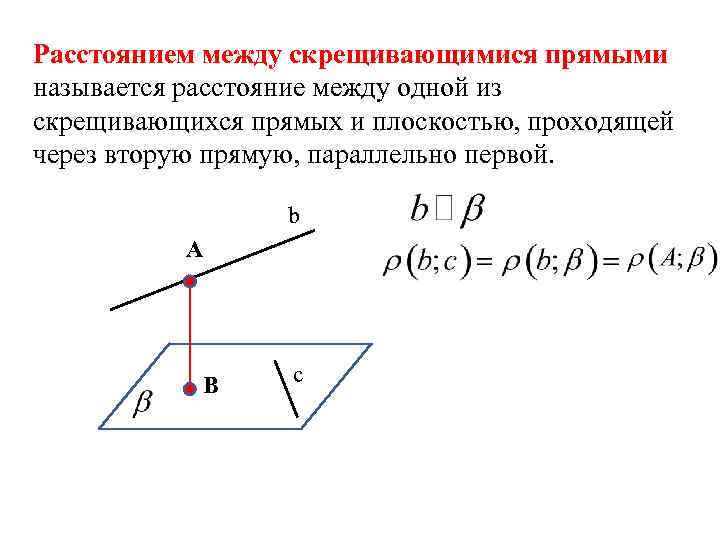Расстоянием между скрещивающимися прямыми называется расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через вторую прямую, параллельно первой. b A B c

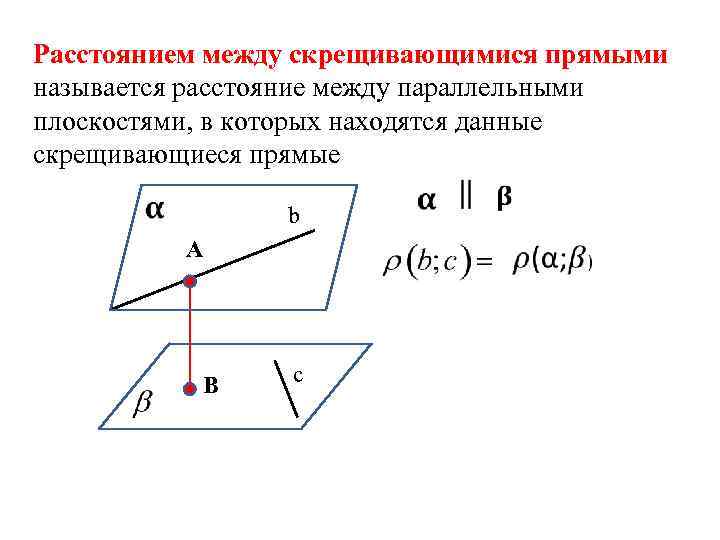Расстоянием между скрещивающимися прямыми называется расстояние между параллельными плоскостями, в которых находятся данные скрещивающиеся прямые b A B c

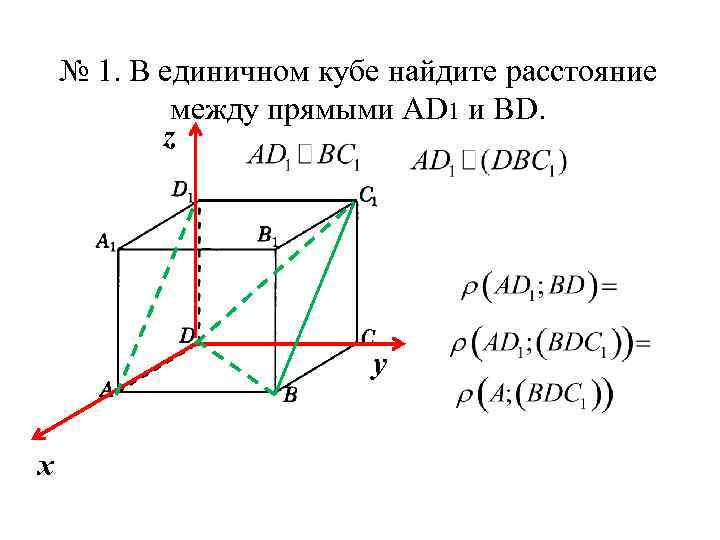№ 1. В единичном кубе найдите расстояние между прямыми АD 1 и ВD. z у х

A (1; 0; 0) D (0; 0; 0) B (1; 1; 0) C 1 (0; 1; 1) Запишем уравнение плоскости BDC 1. Найдем искомое расстояние по формуле

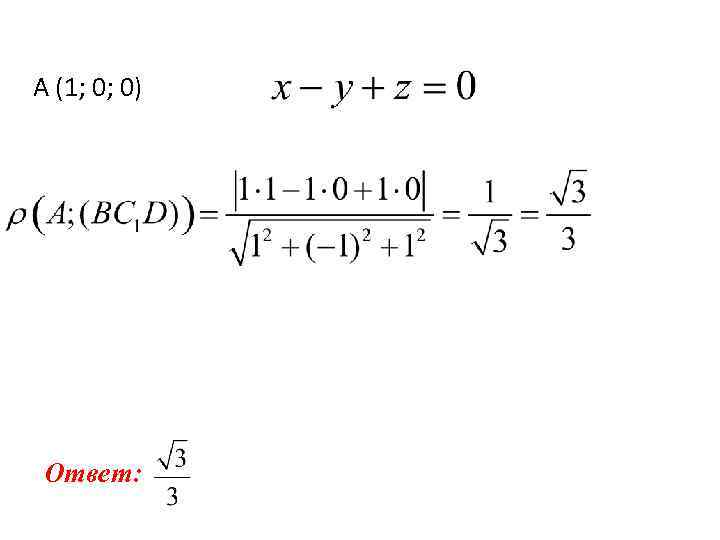A (1; 0; 0) Ответ:

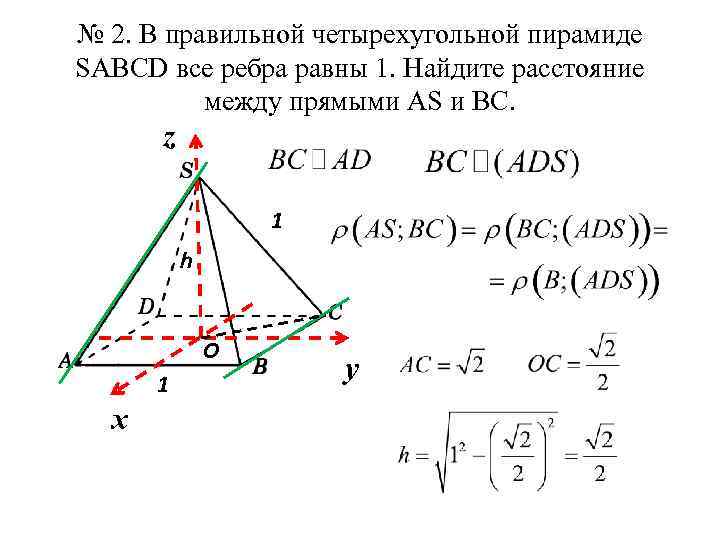№ 2. В правильной четырехугольной пирамиде SABCD все ребра равны 1. Найдите расстояние между прямыми АS и ВС. z 1 h O 1 х y

Запишем уравнение плоскости ADS.

Найдем искомое расстояние по формуле Ответ: