Сортировки Сортировка это упорядочивание набора однотипных

Зарегистрируйтесь, чтобы просмотреть полный документ!

Сортировки

Сортировка – это упорядочивание набора однотипных данных по возрастанию или убыванию. В общем случае сортировку следует понимать как процесс перегруппировки заданного множества объектов в определенном порядке. Часто при сортировке больших объемов данных нецелесообразно переставлять сами элементы, поэтому для решения задачи выполняется упорядочивание элементов по индексам. То есть индексы элементов выстраивают в такой последовательности, что соответствующие им значения элементов оказываются отсортированными по условию задачи. Сортировка применяется для облегчения поиска элементов в упорядоченном множестве. Задача сортировки одна из фундаментных в программировании.

Чаще всего при сортировке данных лишь часть их используется в качестве ключа сортировки. Ключ сортировки – это часть данных, определяющая порядок элементов. Таким образом, ключ участвует в сравнениях, но при обмене элементов происходит перемещение всей структуры данных. Например, в списке почтовой рассылки в качестве ключа может использоваться почтовый индекс, но сортируется весь адрес. При решении задач сортировок массивов ключ и данные совпадают.

Оценка алгоритмов сортировки Существует множество различных алгоритмов сортировки. Все они имеют свои положительные и отрицательные стороны. Перечислим общие критерии оценки алгоритмов сортировки. • Скорость работы алгоритма сортировки. Она непосредственно связана с количеством сравнений и количеством обменов, происходящих во время сортировки, причем обмены занимают больше времени. Сравнение происходит тогда, когда один элемент массива сравнивается с другим; обмен происходит тогда, когда два элемента меняются местами. Время работы одних алгоритмов сортировки растет экспоненциально, а время работы других логарифмически зависит от количества элементов.

• Время работы в лучшем и худшем случаях. Оно имеет значение при анализе выполнения алгоритма, если одна из краевых ситуаций будет встречаться довольно часто. Алгоритм сортировки зачастую имеет хорошее среднее время выполнения, но в худшем случае он работает очень медленно. • Поведение алгоритма сортировки называется естественным, если время сортировки минимально для уже упорядоченного списка элементов, увеличивается по мере возрастания степени неупорядоченности списка и максимально, когда элементы списка расположены в обратном порядке. Объем работы алгоритма оценивается количеством производимых сравнений и обменов.

Различные сортировки массивов отличаются по быстродействию. Существуют простые методы сортировок, которые требуют порядка n*n сравнений, и быстрые сортировки, которые требуют порядка n*ln(n) сравнений. Простые методы удобны для объяснения принципов сортировок, т. к. имеют простые и короткие алгоритмы. Усложненные методы требуют меньшего числа операций, но сами операции более сложные, поэтому для небольших массивов простые методы более эффективны. Простые методы сортировки можно разделить на три основные категории: • сортировка методом "пузырька" (простого обмена); • сортировка простого выбора (простой перебор); • сортировка методом простого включения (сдвигвставка, вставками, вставка и сдвиг).

Сортировка методом "пузырька" (простого обмена) Самый известный алгоритм – пузырьковая сортировка (bubble sort, сортировка методом пузырька или просто сортировка пузырьком). Его популярность объясняется интересным названием и простотой самого алгоритма. Алгоритм попарного сравнения элементов массива в литературе часто называют "методом пузырька", проводя аналогию с пузырьком, поднимающимся со дна бокала с газированной водой. По мере всплывания пузырек сталкивается с другими пузырьками и, сливаясь с ними, увеличивается в объеме. Чтобы аналогия стала очевидной, нужно считать, что элементы массива расположены вертикально друг над другом, и их нужно так упорядочить, чтобы они увеличивались сверху вниз.

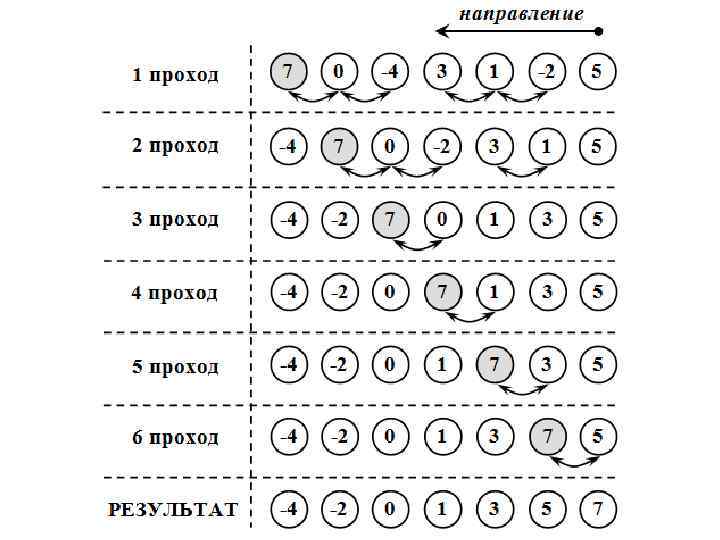
Алгоритм состоит в повторяющихся проходах по сортируемому массиву. За каждый проход элементы последовательно сравниваются попарно и, если порядок в паре неверный, выполняется обмен элементов. Проходы по массиву повторяются до тех пор, пока на очередном проходе не окажется, что обмены больше не нужны, что означает – массив отсортирован. При проходе алгоритма элемент, стоящий не на своём месте, "всплывает" до нужной позиции

//Описание функции сортировки методом "пузырька" void Bubble. Sort (int k, int x[max]) { int i, j, buf; for (i=k-1; i>0; i--) for (j=0; j<i; j++) if (x[j]>x[j+1]) { buf=x[j]; x[j]=x[j+1]; x[j+1]=buf; } }

в одном направлении, в последовательных проходах можно чередовать направления. Таким образом, элементы, сильно удаленные от своих положений, быстро станут на свои места. Данная версия пузырьковой сортировки носит название шейкер-сортировки (shaker sort сортировка перемешиванием, сортировка взбалтыванием, сортировка встряхиванием), поскольку действия, производимые ею с массивом, напоминают взбалтывание или встряхивание. Ниже показана реализация шейкерсортировки. //Описание функции шейкер-сортировки void Shaker(int k, int x[max]) { int i, t; bool exchange;

do { } exchange = false; for(i=k-1; i > 0; --i) { if(x[i-1] > x[i]) { t = x[i-1]; x[i-1] = x[i]; x[i] = t; exchange = true; } }

for(i=1; i < k; ++i) { if(x[i-1] > x[i]) { t = x[i-1]; x[i-1] = x[i]; x[i] = t; exchange = true; } } } while(exchange); //сортировать до тех пор, пока не будет обменов Хотя шейкер-сортировка и является улучшенным вариантом по сравнению с пузырьковой сортировкой, она по-прежнему имеет время выполнения порядка N 2.

Сортировка методом простого выбора (простой перебор) Это наиболее естественный алгоритм упорядочивания. При данной сортировке из массива выбирается элемент с наименьшим значением и обменивается с первым элементом. Затем из оставшихся n - 1 элементов снова выбирается элемент с наименьшим ключом и обменивается со вторым элементом, и т. д. Шаги алгоритма: 1. находим минимальное значение в текущей части массива; 2. производим обмен этого значения со значением на первой неотсортированной позиции; 3. далее сортируем хвост массива, исключив из рассмотрения уже отсортированные элементы.

//Описание функции сортировки методом простого выбора void Selection. Sort (int k, int x[max]) { int i, j, min, temp; for (i=0; i<k-1; i++) { min=i; //устанавливаем начальное значение мин. индекса for (j=i+1; j<k; j++) //ищем мин. индекс элемента { if (x[j]<x[min]) min=j; //меняем значения местами } temp=x[i]; x[i]=x[min]; x[min]=temp; } }

Сортировка методом простого включения (сдвиг-вставка, вставками, вставка и сдвиг) Хотя этот метод сортировки намного менее эффективен, чем сложные алгоритмы (такие как быстрая сортировка), у него есть ряд преимуществ: • прост в реализации; • эффективен на небольших наборах данных, на наборах данных до десятков элементов может оказаться лучшим; • эффективен на наборах данных, которые уже частично отсортированы; • это устойчивый алгоритм сортировки (не меняет порядок элементов, которые уже отсортированы); • может сортировать массив по мере его получения; • не требует временной памяти, даже под стек.

На каждом шаге алгоритма выбираем один из элементов входных данных и вставляем его на нужную позицию в уже отсортированной последовательности до тех пор, пока набор входных данных не будет исчерпан. Метод выбора очередного элемента из исходного массива произволен; может использоваться практически любой алгоритм выбора.

//Описание функции сортировки методом простого включения void Insert. Sort (int k, int x[max]) { int i, j, temp; for (i=0; i<k; i++) { //цикл проходов, i - номер прохода temp=x[i]; //поиск места элемента for (j=i-1; j>=0 && x[j]>temp; j--) x[j+1]=x[j]; //сдвигаем элемент вправо, пока не дошли //место найдено, вставить элемент x[j+1]=temp;

Улучшенные методы сортировки Метод Шелла является усовершенствованием метода простого включения, который основан на том, что включение использует любой частичный порядок. Но недостатком простого включения является то, что во внутреннем цикле элемент A[i] фактически сдвигается на одну позицию. И так до тех пор, пока он не достигнет своего места в отсортированной части. (На самом деле передвигалось место, оставленное под A[i]). Метод Шелла позволяет преодолеть это ограничение. Вместо включения A[i] в подмассив предшествующих ему элементов, его включают в подсписок, содержащий элементы A[i – h], A[i – 2 h], A[i – 3 h] и так далее, где h – положительная константа. Таким образом, формируется массив, в котором «h-серии» элементов, отстоящие друг от друга на h, сортируются отдельно. Конечно, этого недостаточно: процесс возобновляется с новым значением h, меньшим предыдущего. И так до тех пор, пока не будет достигнуто значение h = 1.

$void s_shell(int mass[], int n) { int i, j, t; int d=m/2; //выбираем первоначальное$

void s_shell(int mass[], int n) { int i, j, t; int d=m/2; //выбираем первоначальное расстояние между сравниваемыми элементами while(d>0) { for(int i=0; i<p-d; i++) { j=i; while(j>=0 && mass[j]>mass[j+d]) //если впередистоящий элемент больше второго, то производим замену { n=mass[j]; mass[j]=mass[j+d]; mass[j+d]=n; j--; //уменьшаем j на 1, чтобы просмотреть все элементы, стоящие слева от текущего и равноотстоящие им на расстояние d } d/=2; }

Сортировка слиянием Алгоритм сортировки, который упорядочивает списки (или другие структуры данных, доступ к элементам которых можно получать только последовательно, например — потоки) в определённом порядке. Сначала задача разбивается на несколько подзадач меньшего размера. Затем эти задачи решаются с помощью рекурсивного вызова или непосредственно, если их размер достаточно мал. Наконец, их решения комбинируются, и получается решение исходной задачи. Для решения задачи сортировки эти три этапа выглядят так: • Сортируемый массив разбивается на две части примерно одинакового размера; • Каждая из получившихся частей сортируется отдельно, например - тем же самым алгоритмом; • Два упорядоченных массива половинного размера соединяются в один. Рекурсивное разбиение задачи на меньшие происходит до тех пор, пока размер массива не достигнет единицы (любой массив длины 1 можно считать упорядоченным).

void slip(int l, int m, int r) { int i=l, j=m+1, k=0; while ((i<=m) && (j<=r)) { if (a[i]<a[j]) { c[k]=a[i]; i++; k++; } else {c[k]=a[j]; j++; k++; } } while (i<=m) {c[k]=a[i]; i++; k++; } while (j<=r) {c[k]=a[j]; j++; k++; } for (k=0, i=l; i<=r; i++, k++) a[i]=c[k]; }

$void s_sl(int l, int r) { } if (l < r) { int m=(l+r)/2;$

void s_sl(int l, int r) { } if (l < r) { int m=(l+r)/2; s_sl(l, m); s_sl(m+1, r); slip(l, m, r); }

Быстрая сортировка использует стратегию «разделяй и властвуй» . Шаги алгоритма таковы: • Выбираем в массиве некоторый элемент, который будем называть опорным элементом. С точки зрения корректности алгоритма выбор опорного элемента безразличен. С точки зрения повышения эффективности алгоритма выбираться должна медиана, но без дополнительных сведений о сортируемых данных её обычно невозможно получить. Известные стратегии: выбирать постоянно один и тот же элемент, например, средний или последний по положению; выбирать элемент со случайно выбранным индексом. • Операция разделения массива: реорганизуем массив таким образом, чтобы все элементы, меньшие или равные опорному элементу, оказались слева от него, а все элементы, большие опорного — справа от него. Обычный алгоритм операции:

1. Два индекса — l и r, приравниваются к минимальному и максимальному индексу разделяемого массива соответственно. 2. Вычисляется индекс опорного элемента m. 3. Индекс l последовательно увеличивается до m до тех пор, пока lй элемент не превысит опорный. 4. Индекс r последовательно уменьшается до m до тех пор, пока rй элемент не окажется меньше опорного. 5. Если r = l — найдена середина массива — операция разделения закончена, оба индекса указывают на опорный элемент. 6. Если l < r — найденную пару элементов нужно обменять местами и продолжить операцию разделения с тех значений l и r, которые были достигнуты. Следует учесть, что если какая-либо граница (l или r) дошла до опорного элемента, то при обмене значение m изменяется на r-й или l-й элемент соответственно.

Рекурсивно упорядочиваем подмассивы, лежащие слева и справа от опорного элемента. Базой рекурсии являются наборы, состоящие из одного или двух элементов. Первый возвращается в исходном виде, во втором, при необходимости, сортировка сводится к перестановке двух элементов. Все такие отрезки уже упорядочены в процессе разделения.

void qsort(int l, int r) { int w, x, i, j; i=l; j=r; x=a[(l+r)/2]; while (i<=j) { while ( a[i]<x) i++; while (x<a[j]) j--; if (i<=j) { w=a[i]; a[i]=a[j]; a[j]=w; i++; j--; } } if (l<j) qsort(l, j); if (i<r) qsort(i, r); }

Поиск в массиве структур Линейный поиск в массивахэффективен в массивах, с небольшим количеством элементов, причём элементы в таких массивах никак не отсортированы и не упорядочены. Алгоритм линейного поиска в массивах последовательно проверяет все элементы массива и сравнивает их с ключевым значением. Таким образом, в среднем необходимо проверить половину значений в массиве, чтобы найти искомое значение. Чтобы убедиться, в отсутствии искомого значения необходимо проверить все элементы массива. int p_lin 1(int a[], int n, int x) { for(int i=0; i < n; i++) if (a[i]==x) return i; return -1; }

$int p_lin 2(int a[], int n, int x) { a[n]=x; int i=0; while (a[i]!=x)$

int p_lin 2(int a[], int n, int x) { a[n]=x; int i=0; while (a[i]!=x) i++; if (i==n) return -1; else return i; }

Поиск делением пополам Двоичный(бинарный) поиск — алгоритм поиска элемента в отсортированном массиве. Двоичный поиск можно использовать только в том случае, если есть массив, все элементы которого упорядочены (отсортированы). Бинарный поиск не используется для поиска максимального или минимального элементов, так как в отсортированном массиве эти элементы содержатся в начале и в конце массива соответственно, в зависимости от тога как отсортирован массив, по возрастанию или по убыванию. Поэтому алгоритм бинарного поиска применим, если необходимо найти некоторый ключевой элемент в массиве. То есть организовать поиск по ключу, где ключ — это определённое значение в массиве.

$int p_dv(int a[], int n, int x) { int i=0, j=n-1, m; while(i<j) {$

int p_dv(int a[], int n, int x) { int i=0, j=n-1, m; while(i<j) { m=(i+j)/2; if (x > a[m]) i=m+1; else j=m; } if (a[i]==x) return i; else return -1; }

Интерполяционный поиск Интерполирующий поиск, напоминает двоичный поиск, за исключением того, что вместо деления области поиска на две части, интерполирующий поиск производит оценку новой области поиска по расстоянию между ключом поиска и текущим значением элемента. Иными словами, двоичный поиск учитывает лишь знак разности между ключом поиска и текущим значением, а интерполирующий поиск еще учитывает и модуль этой разности и по данному значению производит предсказание позиции следующего элемента для проверки. По скорости поиска интерполирующий поиск превосходит двоичный. Также существенным отличием от двоичного является то, что с помощью алгоритма интерполирующего поиска можно искать не только числовые значения, но и, к примеру, текстовую информацию.

$int p_dv(int a[], int n, int x) { int i=0, j=n-1, m; while(i<j) {$

int p_dv(int a[], int n, int x) { int i=0, j=n-1, m; while(i<j) { if (a[i]==a[j]) if (a[i]==x) return i; else return -1; m=i+(j-i)*(x-a[i])/(a[j]-a[i]); if (a[m]==x) return m; else if (x > a[m]) i=m+1; else j=m-1; } return -1; }

Скачать презентацию Сортировки Сортировка это упорядочивание набора однотипных

Тема 11 - Сортировки, Поиск .ppt

Количество слайдов: 37