СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА

СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА

Синус, косинус, тангенс острого угла прямоугольного треугольника

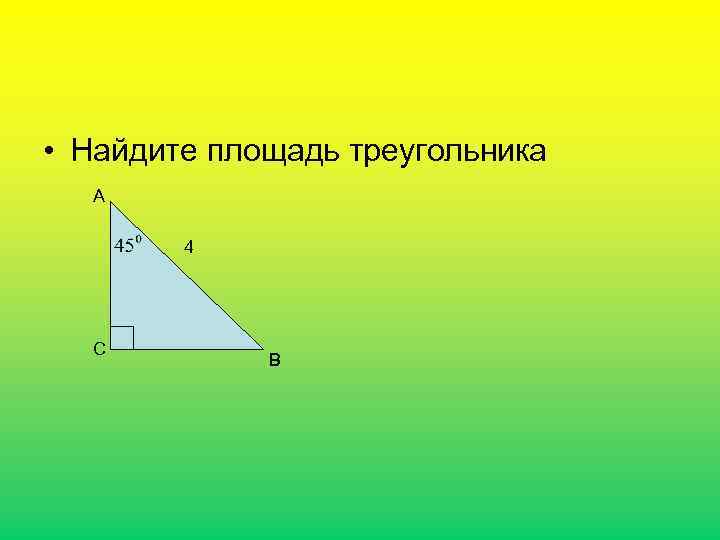• Найдите площадь треугольника А 4 С В

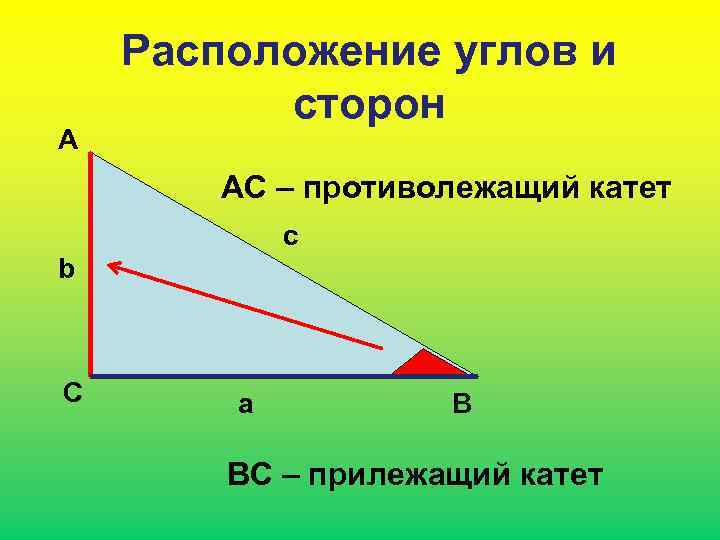А Расположение углов и сторон АС – противолежащий катет c b С a В ВС – прилежащий катет

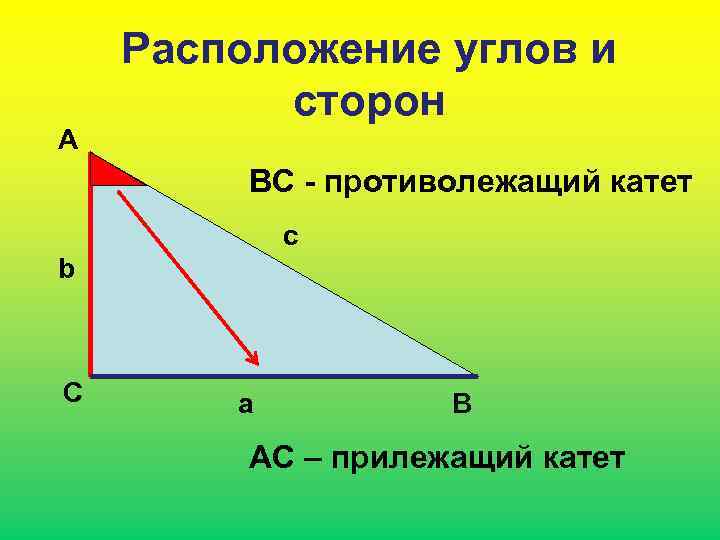А Расположение углов и сторон ВС - противолежащий катет c b С a В АС – прилежащий катет

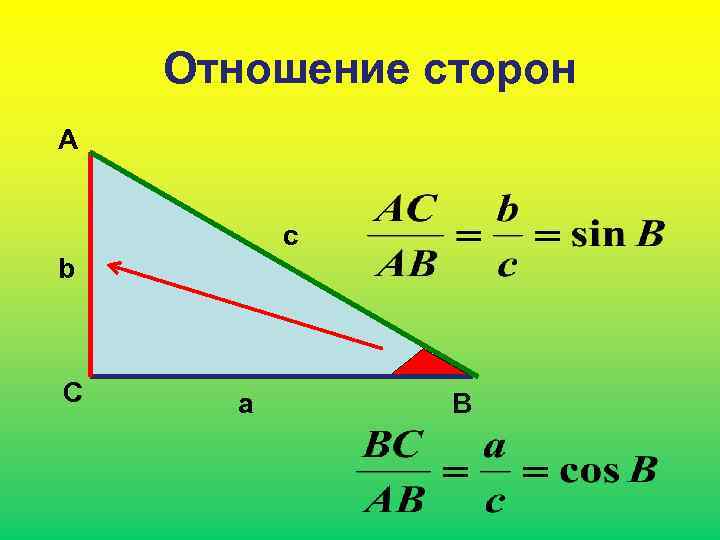Отношение сторон А c b С a В

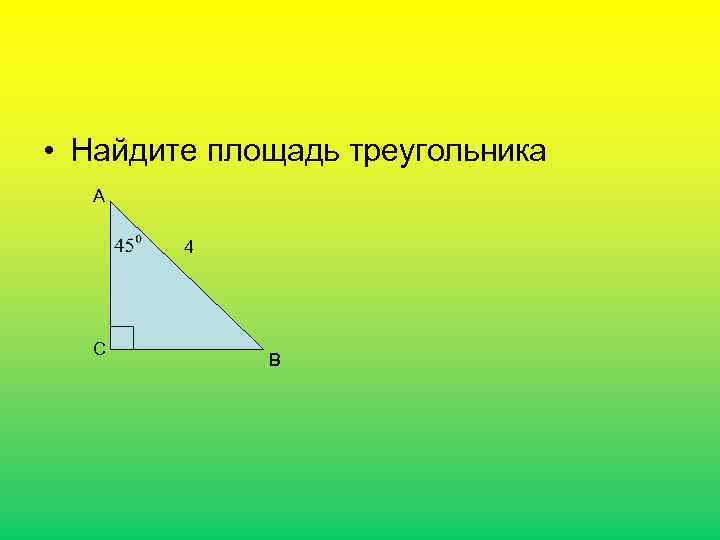• Найдите площадь треугольника А 4 С В

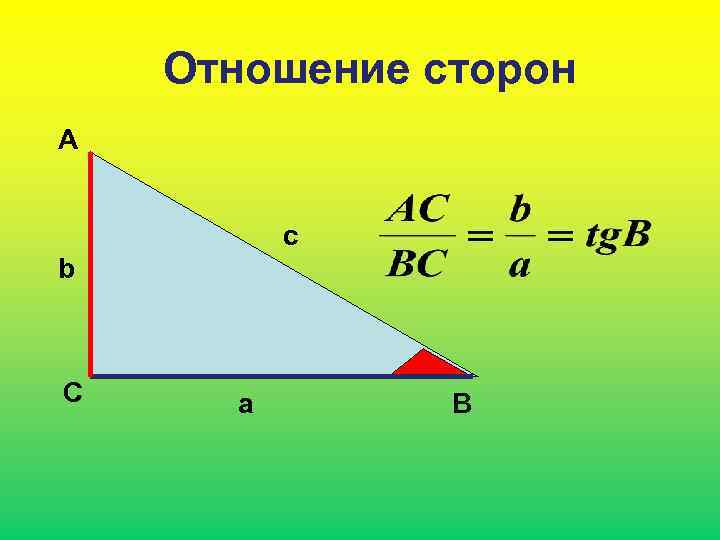Отношение сторон А c b С a В

Тангенсом острого угла • Синусом острого угла в Косинусом острого в прямоугольном угла в прямоугольном треугольнике называется отношение противолежащего прилежащего катета к противолежащего катета к прилежащему гипотенузе катета к гипотенузе катету

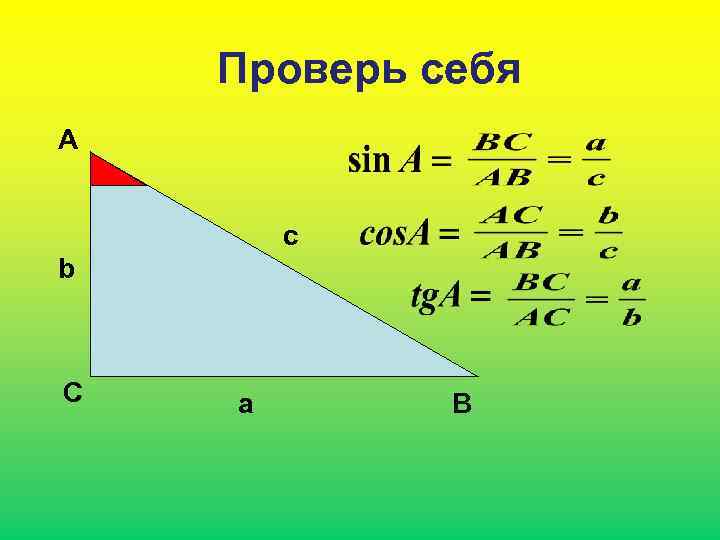Проверь себя А c b С a В

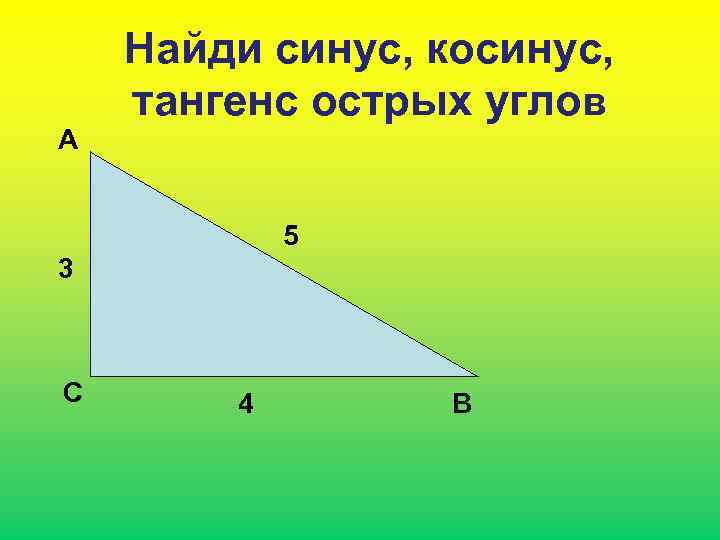А Найди синус, косинус, тангенс острых углов 5 3 С 4 В

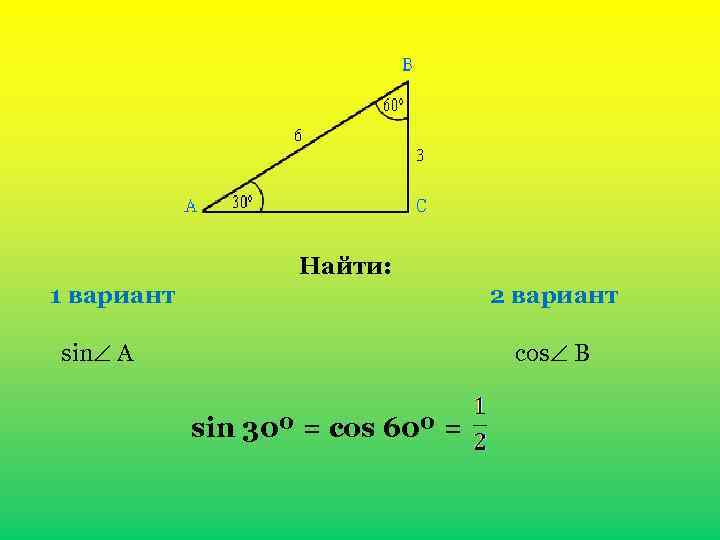Найти: 1 вариант 2 вариант sin A cos B sin 30º = cos 60º =

Вопрос • Каким числом может быть синус острого угла в прямоугольном треугольнике? • Может ли синус угла быть равен 2? 1. 7? 0. 3?

Вопрос • Каким числом может быть синус острого угла в прямоугольном треугольнике? • Может ли синус угла быть равен 2? 1. 7? 0. 3? • Синус угла всегда меньше 1. ( 0. 5, 0. 9, 0. 32)

Вопрос. 1. Каким числом может быть косинус угла ? 2. Может ли косинус данного угла быть равным 10? 1? 0, 8? 3. От чего зависит косинус угла?

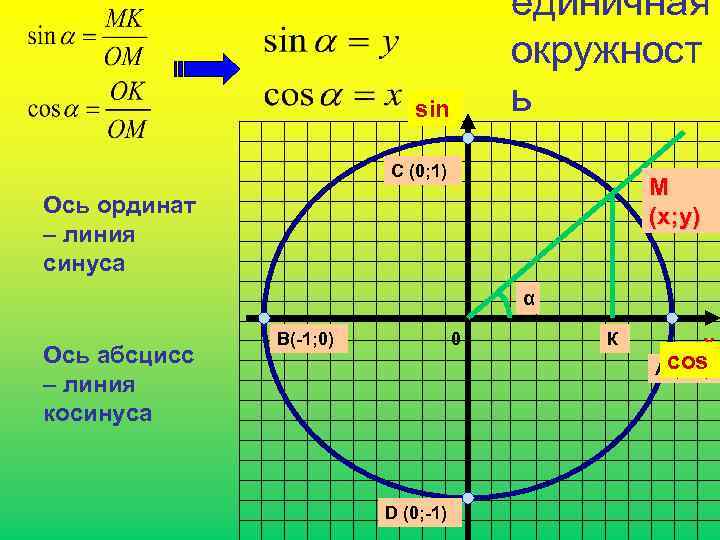sin. Y Ось абсцисс – линия косинуса Ось ординат – линия синуса единичная окружност ь С (0; 1) К 0 D (0; -1) В(-1; 0) α М (х; у) X (1; 0) Аcos

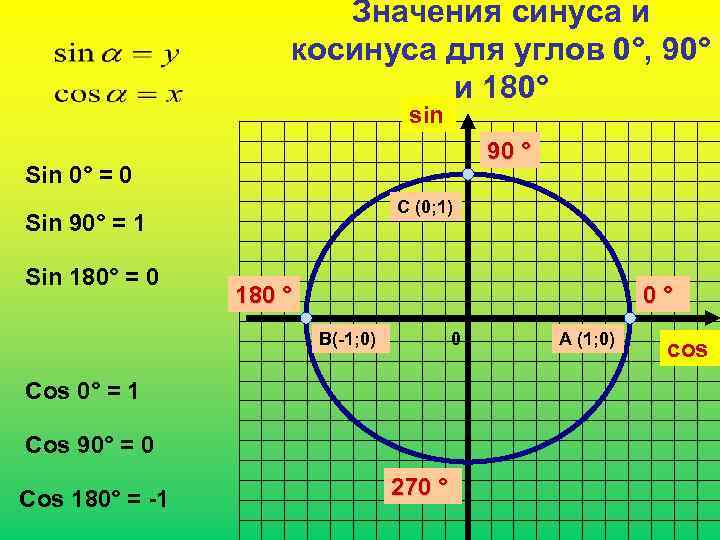Значения синуса и косинуса для углов 0°, 90° и 180° sin Sin 180° = 0 Sin 90° = 1 Sin 0° = 0 180 ° 0 ° 0 С (0; 1) 90 ° Cos 180° = -1 Cos 90° = 0 Cos 0° = 1 В(-1; 0) 270 ° А (1; 0) cos

Синус, косинус, тангенс угла sin = y. cos = x. Тангенс, катангенс угла Т. к. tg = 0 ≤ ≤ 180 ctg = ,

Уравнение окружности х2 + у 2 = 1 sin = x, cos = y 0 ≤ ≤ 180

• Найдите sin A, если cos A=1/2

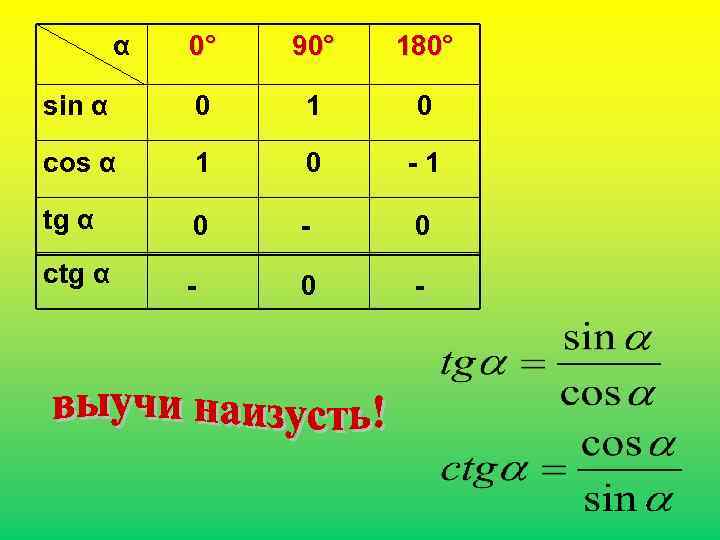α 0° 90° 180° sin α 0 1 0 cos α 1 0 -1 tg α 0 - 0 ctg α - 0 -

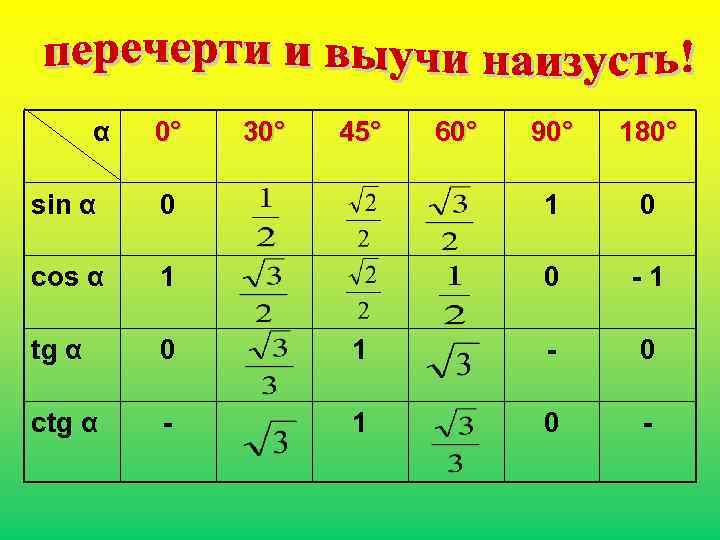α 0° 30° 45° 60° 90° 180° sin α 0 1 0 cos α 1 0 -1 tg α 0 1 - 0 ctg α - 1 0 -

Домашняя работа • П 93 изучить, выучить определения и таблицу( можно взять с группы в контакте или в факультативах), № 1013, 1014(б), 1015(б)

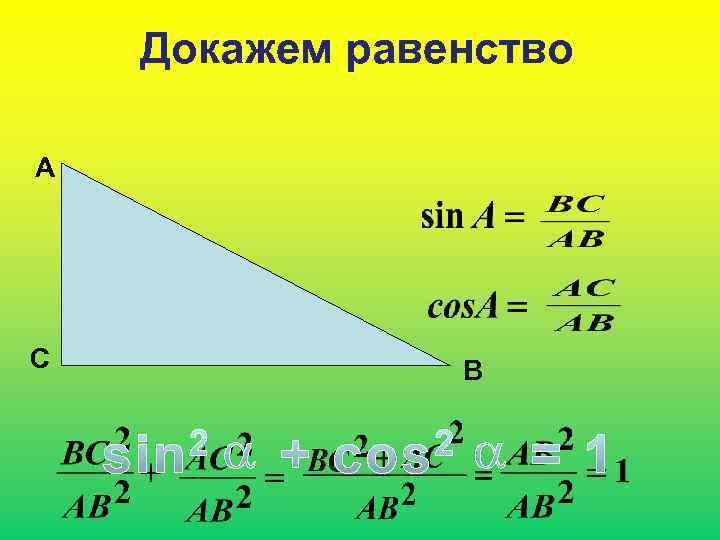Докажем равенство А С В

Основное тригонометрическое тождество Тригонометрия - измерение треугольников

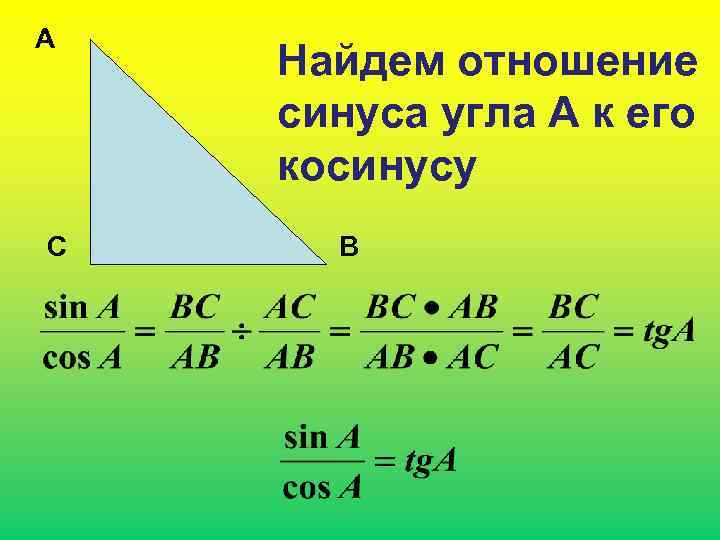А С Найдем отношение синуса угла А к его косинусу В

Тангенс угла равен отношению синуса к косинусу этого угла