lecture_8.ppt
- Количество слайдов: 21
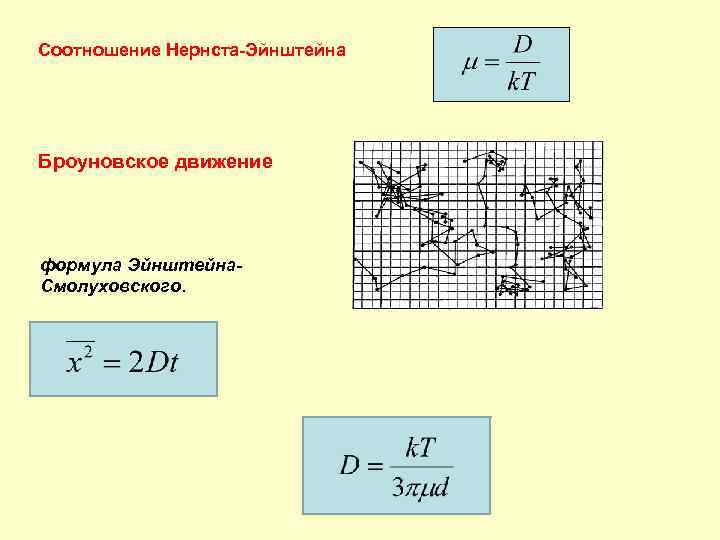
Соотношение Нернста-Эйнштейна Броуновское движение формула Эйнштейна. Смолуховского.

Коэффициент диффузии. При обычных давлениях В области вакуума, где λ определяется размерами сосуда Коэффициент вязкости. Коэффициент теплопроводности.

ОСНОВЫ ТЕРМОДИНАМИКИ. Работа и теплота. Первое начало термодинамики. Наряду с механической энергией направленного движения тело обладает внутренней энергией хаотического теплового движения, при котором скорости отдельных молекул и расстояния между ними различны и непрерывно изменяются Величина внутренней энергии тела складывается из кинетической энергии хаотического движения молекул и потенциальной энергии их взаимного расположения Для идеального газа, состоящего из N молекул, второй член равен нулю и где i- число степеней свободы, рассматриваемого газа.

В отличие от механической энергии энергия теплового движения распределяется между отдельными молекулами хаотически, большим числом непрерывно сменяющих друга способов. Эта совокупность микросостояний, характеризует определенное макроскопическое состояние всего тела в целом с определенной температурой Т, объемом V и давлением р. При данном состоянии всего тела оно обладает вполне определенными значениями механической Емех и внутренней U энергий. Если привести в соприкосновение два тела, то в процессе взаимодействия они смогут обмениваться энергией как в той, так и в другой форме. Этот обмен различными формами энергии характеризуется соответственно понятиями совершенной работы А и переданного тепла Q. При этом количество переданной механической энергии мы измеряем совершенной работой. Пример: механическая энергия турбины.

Когда топочные газы обогревают паровой котел, они охлаждаются. В свою очередь вода в котле нагревается — возрастает энергия теплового движения молекул воды. При этом оба тела (газ и вода) обмениваются энергией своих внутренних тепловых движений. Величину переданной энергии теплового движения молекул мы измеряем количеством теплоты. Следовательно, теплота, так же как и работа, не является особой формой энергии. Энергия механического движения может превращаться в энергию теплового движения и обратно. Камень, падающий на землю, в момент удара отдает всю накопленную им кинетическую энергию, за счет чего оба тела нагреваются. В качестве обратного примера можно рассмотреть расширяющийся газ, заключенный в сосуд с поршнем. Молекулы газа, движущиеся со средними скоростями v 1 ударяются о поршень и отлетают назад с меньшей скоростью: v 2=v 1 -2 u (решали подобную задачу) Таким образом, в процессе расширения газа его внутренняя энергия уменьшается вследствие превращения в механическую энергию движущегося поршня.

Можно без труда найти множество примеров превращения одной формы энергии в другую. Опыт показывает, что во всех приведенных и в других многочисленных примерах превращение механической энергии в тепловую и обратно совершается всегда в строго эквивалентных количествах. Такая общая формулировка этого закона носит название первого начала термодинамики. Рассмотрим тело, в целом неподвижное, например, газ в цилиндре с подвижным поршнем. Внутреннюю энергию теплового движения этого тела обозначим через U. В процессе взаимодействия с рассматриваемым телом изменится интенсивность теплового движения молекул окружающих тел: эти тела охладятся или нагреются и, тем самым, передадут рассматриваемому телу некоторое количество теплоты Q. Знак - величины Q будет указывать направление процесса теплообмена. При изменении внутренней энергии изменится состояние тела, оно будет расширяться или сжиматься и приведет в механическое движение окружающие его тела.

Количество переданной окружающим телам энергии механического движения мы будем характеризовать работой А, совершенной рассматриваемым телом над окружающими его телами. Работа А также является величиной алгебраической и имеет знак. Чаще всего применяемое правило знаков. Q считается положительным, если тепло передается от окружающей среды данному телу, т. е. за счет притока тепла Q извне внутренняя энергия тела возрастает. Наоборот, А считается положительной, если тело производит механическую работу над окружающими телами, т. е. за счет произведенной механической работы убывает внутренняя энергия тела. Первый закон термодинамики. Изменение внутренней энергии тела U равно разности сообщенного телу количества теплоты Q и произведенной внешними силами механической работы А

Можно переписать и в таком виде: Количество теплоты, сообщенное телу ( Q), идет на увеличение его внутренней энергии ( U) и на совершение телом работы ( А). Видно, что никакой другой разницы между теплотой и работой (энергией) нет. Поэтому они должны измеряться в одних и тех же единицах. В системе СИ за единицу количества теплоты принят 1 джоуль (Дж, ), а тепло принято измерять в калориях: 1 калория=4, 1868 Дж Работа при изменении объема газа. Пусть под действием приложенной внешней силы F поршень опустился на расстояние dx, сжав при этом газа и равной p. S, где р — давление газа. Работа d. A, затраченная на перемещение поршня на расстояние dx, равна, очевидно, Fdx=p. Sdx (р-давление газа). Но Sdx есть не что иное, как изменение объема d. V=-Sdx, следовательно,

Можно вычислить внешнюю работу и в том случае, когда изменение параметров состояния не бесконечно мало. Если тело переходит из состояния / в состояние 2, то связанная с этим работа А определяется путем интегрирования уравнения Графически этот интеграл равен заштрихованной площади под этой кривой. Если переход из состояния 1 в состояние 2 происходит так, что изменение давления с объемом изображается кривой II, то связанная с этим - переходом работа будет другой. Работа, произведенная телом (или над ним) при изменении его объема, зависит от последовательности состояний, которую проходит тело от начального в конечное состояние. Что касается внутренней энергии U, то она зависит только от состояния (функция состояния) тела и ее изменение не зависит от промежуточных состояний, уравнение первого закона можно записать, как

В частном случае, если тело в результате всех изменений состояния вернулось в исходное состояние, т. е. U 1 = U 2, то в этом случае говорят, что процесс изменения состояния — круговой, или циклический. Очевидно, что при циклическом процессе произведенное работа равно суммарной величине переданного тепла. Квазистатические процессы. Если расширение или сжатие газа происходит быстро, то давления в разных его частях не успевают выравниваться и газ не находится в состоянии равновесия. Для того чтобы в процессе изменения газ находился в равновесии, необходимо, чтобы этот процесс протекал весьма медленно, в пределе — бесконечно медленно. Такие процессы называются квазистатическими. Если процесс изменения объема, т. е. сжатие или расширение газа, происходит неквазистатически, то совершенная при сжатии или расширении работа будет меньше, чем при процессе квазистатическом!!!

Теплоемкость газа. Если для увеличения температуры тела на ΔT градусов необходимо сообщить ему ΔQ джоулей, то средняя теплоемкость тела в интервале ΔT равна Теплоемкость тела пропорциональна массе и зависит от вещества тела. Удельная теплоемкость Суд данного вещества характеризуется количеством теплоты, необходимым для нагревания 1 кг данного вещества на один градус, и измеряется в Дж/(кг К). Для газов удобно пользоваться молярной теплоемкостью (размерность Дж/моль К) Если мы будем нагревать газ, заключенный в замкнутом объеме, V = const , то все подводимое тепло ΔQ будет идти только на увеличение внутренней энергии газа. Тогда в ΔА = 0 и, следовательно,

Если мы хотим, чтобы в процессе нагревания сохранялось давление, газу следует предоставить возможность расширяться. Для этого поместим газ в цилиндр с поршнем, на который действует постоянное давление р = const. При нагревании газа до той же температуры часть подводимого тепла расходуется теперь на работу против внешних сил при расширении газа. Теплоемкость ΔQ/ΔT газа при постоянном давлении, которую мы обозначим через Ср, будет больше, чем CV. Таким образом, количество теплоты ΔQ, необходимое для нагревания газа на ΔТК, существенно зависит от дополнительных условий — характера изменения других макроскопических параметров и каждому процессу отвечает своя теплоемкость С. Величины Ср и Cv для идеального газа оказываются связанными простым соотношением. Для вывода этого соотношения рассмотрим сначала 1 моль идеального газа, нагреваемый при постоянном объеме.
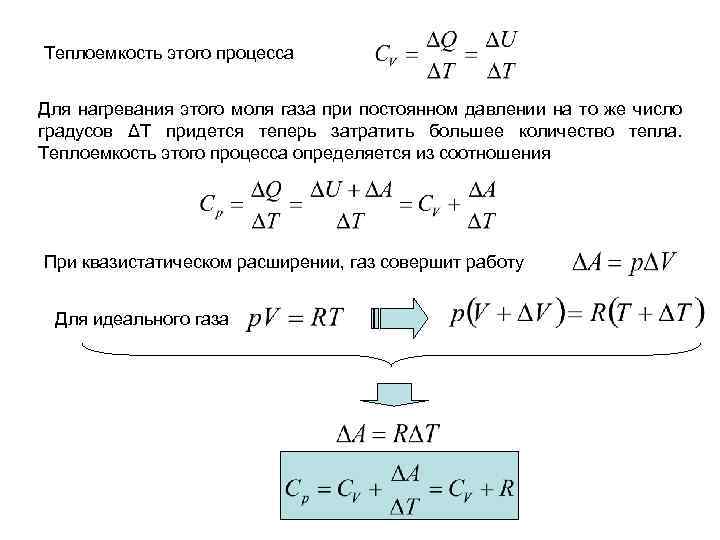
Теплоемкость этого процесса Для нагревания этого моля газа при постоянном давлении на то же число градусов ΔТ придется теперь затратить большее количество тепла. Теплоемкость этого процесса определяется из соотношения При квазистатическом расширении, газ совершит работу Для идеального газа

или Для идеального газа молярная теплоемкость при постоянном давлении превышает молярную теплоемкость при постоянном объеме на величину R, т. е. на 8, 31 к. Дж/(кмоль-К). Это соотношение носит название формулы Майера. Ранее было показано, что теплоемкость многоатомного газа при постоянном объеме CV равна: где i число степеней свободы Очевидно, что теплоемкость этого газа при постоянном давлении, равна

Процессы и циклы с газами и их графическое изображение Разберем детальнее несколько простейших представляющих также и технический интерес. процессов 1. Изохорический процесс. Так называется процесс, при котором объем газа остается постоянным. Так как V = const, то ΔV = 0 и т. е. все сообщаемое газу тепло идет на увеличение его внутренней энергии. Молярная теплоемкость при изохорическом процессе очевидно равна с газами,

2. Изобарический процесс. Так называется про- процесс, проходящий при постоянном давлении (р = const). На р. V-диаграмме этот процесс изображается горизонтальной прямой, параллельной оси V Работа при изобарическом расширении изображается на этом графике площадью прямоугольника : Подводимое к газу тепло частично тратится на увеличение его внутренней энергии (на нагревание), а частично — на совершение работы. Молярная теплоемкость при изобарическом процессе равна Ср При изобарическом сжатии направление процесса меняется на обратное, и работа, совершенная газом, становится отрицательной (ΔА<0).

3. Изотермический процесс. Так называется процесс, проводимый при постоянной температуре газа Т = const). Из уравнения Менделеева — Клапейрона следует, что при этом Это уравнение изображается на графике гиперболой. Поскольку внутренняя энергия идеального газа зависит только от его температуры, то при изотермическом расширении V = const и ΔU = 0. Следовательно, согласно первому началу Работа при этом процессе равна Теплоемкость при изотермическом расширении определяется формально по общему соотношению и равна

Бесконечная теплоемкость не является физическим абсурдом. Она означает, что подводимое к газу тепло не приводит к изменению его температуры в силу того, что все оно идет на совершение газом внешней работы. При расширении ΔQ > 0 и Ст = + при сжатии ΔQ < 0 и Ст = —. Осуществление изотермического процесса при температуре Т предполагает существование — при той же температуре —внешней среды, обладающей неизмеримо большим запасом внутренней энергии, чем внутренняя энергия рабочего газа. 4. Адиабатический процесс. Если сосуд с расширяющимся газом теплоизолировать от окружающей среды, то теплообмен будет отсутствовать, т. е. ΔQ = 0. Процесс, происходящий при соблюдении этого условия, называется адиабатическим. Уравнение первого начала при учете условия ΔQ = 0 принимает вид

Следовательно, при адиабатическом процессе работа совершается только за счет внутренней энергии газа. При адиабатическом расширении газ совершает работу, а его внутренняя энергия и, следовательно, температура падают. При адиабатическом сжатии работа газа отрицательна (внешняя среда производит работу над газом), внутренняя энергия и температура газа возрастают. Теплоемкость при адиабатическом процессе Выведем уравнение кривой, изображающей адиабатический процесс на р. Vдиаграмме. Уравнение состояния моля газа имеет вид При бесконечно малом изменении состояния совершаемая работа d. А=pd. V, а изменение внутренней энергии d. U=Cvd. T и, тогда

Из уравнения Менделеева-Клайперона Выражая d. T, находим Принимая во внимание, что для идеального газа Cv + R = Ср, и введя обозначение =Сp/CV >1 имеем Интегрируя и потенцируя, получаем соотношение Это уравнение называется уравнением Пуассона.

Поскольку >1, то кривая, изображаемая этим уравнением, идет круче изотермы. При адиабатическом расширении из точки 1 кривая адиабаты опускается ниже изотермы, т. е. газ охлаждается, а при адиабатическом сжатии кривая поднимается выше изотермы, т. е. газ нагревается. Показатель адиабаты , очевидно, зависит от числа степеней свободы:
lecture_8.ppt