Some basic concepts of Information Theory and Entropy

Some basic concepts of Information Theory and Entropy • • Information theory, IT Entropy Mutual Information Use in NLP Language Models 1

Entropy • Related to the coding theory- more efficient code: fewer bits for more frequent messages at the cost of more bits for the less frequent NLP Language Models 2

EXAMPLE: You have to send messages about the two occupants in a house every five minutes • Equal probability: 0 no occupants 1 first occupant 2 second occupant 3 Both occupants • Different probability Situation no occupants first occupant Probability Code . 5 0 . 125 110 second occupant . 125 111 Both occupants . 25 10 NLP Language Models 3

• • • Let X a random variable taking values x 1, x 2, . . . , xn from a domain de according to a probability distribution We can define the expected value of X, E(x) as the summatory of the possible values weighted with their probability E(X) = p(x 1)X(x 1) + p(x 2)X(x 2) +. . . p(xn)X(xn) NLP Language Models 4

random variable W that can take one Entropy of several values V(W) and a probability distribution P. • Is there a lower bound on the number of bits neede tod encode a message? Yes, the entropy • It is possible to get close to the minimum (lower bound) It is also a measure of our uncertainty about wht the message says (lot of NLP Language bits- uncertain, few - certain) Models • 5

• • • Given an event we want to associate its information content (I) From Shannon in the 1940 s Two constraints: • Significance: • The less probable is an event the more information it contains P(x 1) > P(x 2) => I(x 2) > I(x 1) • Additivity: • • If two events are independent • NLP Language Models I(x 1 x 2) = I(x 1) + I(x 2) 6

• • • NLP Language Models I(m) = 1/p(m) does not satisfy the second requirement I(x) = - log p(x) satisfies both So we define I(X) = - log p(X) 7

• • Let X a random variable, described by p(X), owning an information content I Entropy: is the expected value of I: E(I) Entropy measures information content of a random variable. We can consider it as the average length of the message needed to transmite a value of this variable using an optimal coding. Entropy measures the degree of desorder (uncertainty) of the random variable. NLP Language Models 8

• Uniform distribution of a variable X. • Each possible value xi X with |X| = M has the same probability pi = 1/M • If the value xi is codified in binary we need log 2 M bits of information • Non uniform distribution. • • by analogy Each value xi has a different probability pi Let assume pi to be independent If Mpi = 1/ pi we will need log 2 Mpi = log 2 (1/ pi ) = - log 2 pi bits of information NLP Language Models 9

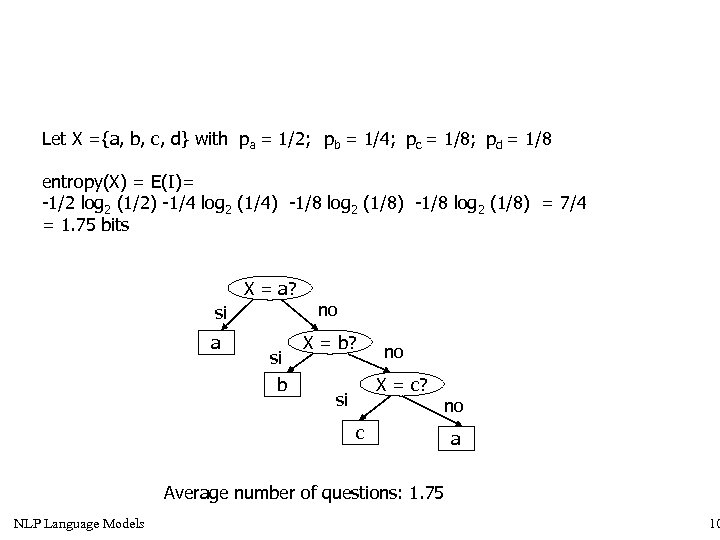
Let X ={a, b, c, d} with pa = 1/2; pb = 1/4; pc = 1/8; pd = 1/8 entropy(X) = E(I)= -1/2 log 2 (1/2) -1/4 log 2 (1/4) -1/8 log 2 (1/8) = 7/4 = 1. 75 bits X = a? si a si b no X = b? no X = c? si no c a Average number of questions: 1. 75 NLP Language Models 10

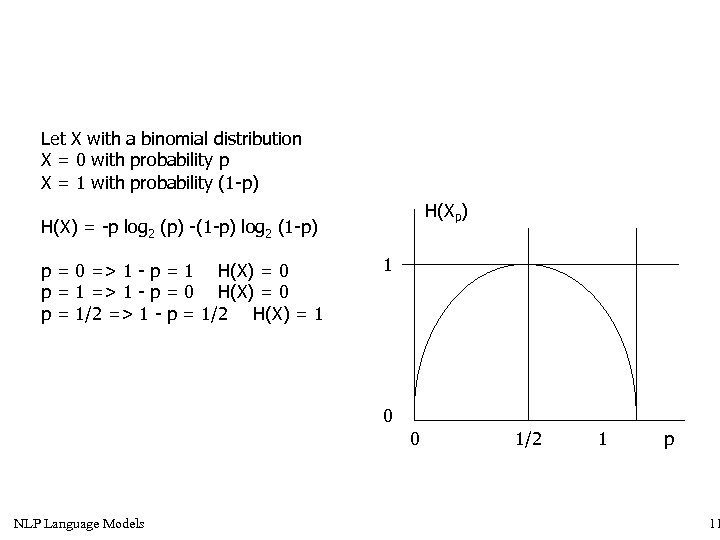
Let X with a binomial distribution X = 0 with probability p X = 1 with probability (1 -p) H(X) = -p log 2 (p) -(1 -p) log 2 (1 -p) p = 0 => 1 - p = 1 H(X) = 0 p = 1 => 1 - p = 0 H(X) = 0 p = 1/2 => 1 - p = 1/2 H(X) = 1 1 0 0 NLP Language Models 1/2 1 p 11

NLP Language Models 12

• joint entropy of two random variables, X, Y is average information content for specifying both variables NLP Language Models 13

• The conditional entropy of a random variable Y given another random variable X, describes what amount of information is needed in average to communicate when the reader already knows X NLP Language Models 14

Chaining rule for probabilities P(A, B) = P(A|B)P(B) = P(B|A)P(A) P(A, B, C, D…) = P(A)P(B|A)P(C|A, B)P(D|A, B, C. . ) NLP Language Models 15

Chaining rule for entropies NLP Language Models 16

Mutual Information • • I(X, Y) is the mutual information between X and Y. I(X, Y) measures the reduction of incertaincy of X when Y is known It measures too the amouny of information X owns about Y (or Y about X) NLP Language Models 17

• I = 0 only when X and Y are independent: • H(X|Y)=H(X) • • H(X)=H(X)-H(X|X)=I(X, X) Entropy is the autoinformation (mutual information between X and X) NLP Language Models 18

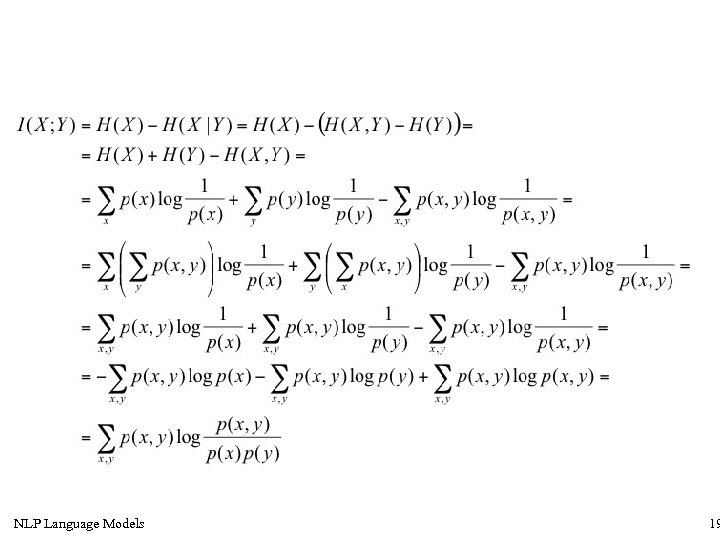
NLP Language Models 19

Pointwise Mutual Information • The PMI of a pair of outcomes x and y belonging to discrete random variables quantifies the discrepancy between the probability of their coincidence given their joint distribution versus the probability of their coincidence given only their individual distributions and assuming independence • The mutual information of X and Y is the expected value of the Specific Mutual Information of all possible outcomes. NLP Language Models 20

• • H: entropy of a language L We ignore p(X) Let q(X) a LM How good is q(X) as an estimation of p(X) ? NLP Language Models 21

Cross Entropy Measures the “surprise” of a model q when it describes events following a distribution p NLP Language Models 22

Relative Entropy Relativa or Kullback-Leibler (KL) divergence Measures the difference between two probabilistic distributions NLP Language Models 23