b4821996958d29c891a0054f9bc35d32.ppt
- Количество слайдов: 26
 Some Application of Statistical Methods in Data Analysis Assoc. Prof. Dr. Abdul Hamid b. Hj. Mar Iman, Former Director, Centre for Real Estate Studies, Universiti Teknologi Malaysia.
Some Application of Statistical Methods in Data Analysis Assoc. Prof. Dr. Abdul Hamid b. Hj. Mar Iman, Former Director, Centre for Real Estate Studies, Universiti Teknologi Malaysia.
 Forms of “statistical” relationship Correlation l Contingency l Cause-and-effect * Causal * Feedback * Multi-directional * Recursive l The last two categories are normally dealt with through regression l
Forms of “statistical” relationship Correlation l Contingency l Cause-and-effect * Causal * Feedback * Multi-directional * Recursive l The last two categories are normally dealt with through regression l
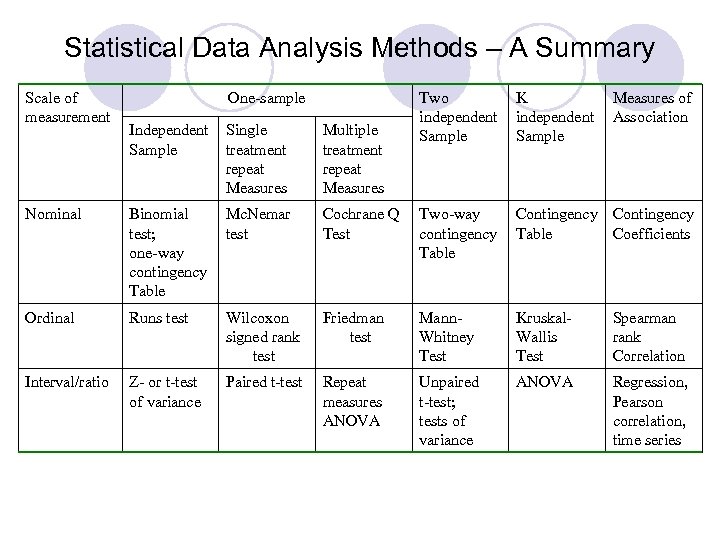 Statistical Data Analysis Methods – A Summary Scale of measurement One-sample Two independent Sample K independent Sample Measures of Association Independent Sample Single treatment repeat Measures Multiple treatment repeat Measures Nominal Binomial test; one-way contingency Table Mc. Nemar test Cochrane Q Test Two-way contingency Table Contingency Table Coefficients Ordinal Runs test Wilcoxon signed rank test Friedman test Mann. Whitney Test Kruskal. Wallis Test Spearman rank Correlation Interval/ratio Z- or t-test of variance Paired t-test Repeat measures ANOVA Unpaired t-test; tests of variance ANOVA Regression, Pearson correlation, time series
Statistical Data Analysis Methods – A Summary Scale of measurement One-sample Two independent Sample K independent Sample Measures of Association Independent Sample Single treatment repeat Measures Multiple treatment repeat Measures Nominal Binomial test; one-way contingency Table Mc. Nemar test Cochrane Q Test Two-way contingency Table Contingency Table Coefficients Ordinal Runs test Wilcoxon signed rank test Friedman test Mann. Whitney Test Kruskal. Wallis Test Spearman rank Correlation Interval/ratio Z- or t-test of variance Paired t-test Repeat measures ANOVA Unpaired t-test; tests of variance ANOVA Regression, Pearson correlation, time series
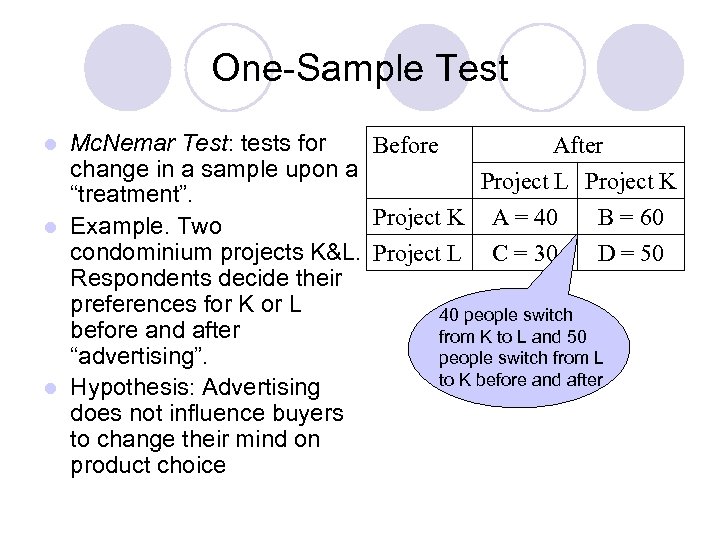 One-Sample Test Mc. Nemar Test: tests for Before After change in a sample upon a Project L Project K “treatment”. Project K A = 40 B = 60 l Example. Two condominium projects K&L. Project L C = 30 D = 50 Respondents decide their preferences for K or L 40 people switch before and after from K to L and 50 “advertising”. people switch from L to K before and after l Hypothesis: Advertising does not influence buyers to change their mind on product choice l
One-Sample Test Mc. Nemar Test: tests for Before After change in a sample upon a Project L Project K “treatment”. Project K A = 40 B = 60 l Example. Two condominium projects K&L. Project L C = 30 D = 50 Respondents decide their preferences for K or L 40 people switch before and after from K to L and 50 “advertising”. people switch from L to K before and after l Hypothesis: Advertising does not influence buyers to change their mind on product choice l
 One-Sample Test (contd. ) l Test statistics: Thus, Q = (40 -45)2/(40+45) rc = 25/85 Q = (0 ij – Eij)2/Eij = 0. 29 i=1 j=1 where E = (A+D)/2 (2 -1); 0. 05 = 3. 84 Therefore, rc Ho not rejected. No influence of advertising on choice of project Q = (0 ij – Eij)2/Eij i=1 j=1 [A-(A+D)/2]2 [D-(A+D)/2]2 (A-D)2 --------- + -------- = ------(A+D)/2 A+D
One-Sample Test (contd. ) l Test statistics: Thus, Q = (40 -45)2/(40+45) rc = 25/85 Q = (0 ij – Eij)2/Eij = 0. 29 i=1 j=1 where E = (A+D)/2 (2 -1); 0. 05 = 3. 84 Therefore, rc Ho not rejected. No influence of advertising on choice of project Q = (0 ij – Eij)2/Eij i=1 j=1 [A-(A+D)/2]2 [D-(A+D)/2]2 (A-D)2 --------- + -------- = ------(A+D)/2 A+D
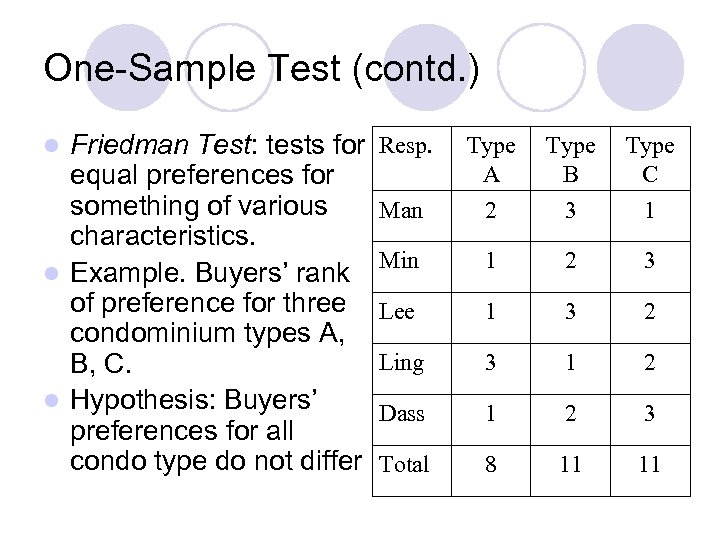 One-Sample Test (contd. ) Friedman Test: tests for equal preferences for something of various characteristics. l Example. Buyers’ rank of preference for three condominium types A, B, C. l Hypothesis: Buyers’ preferences for all condo type do not differ l Resp. Type A Type B Type C Man 2 3 1 Min 1 2 3 Lee 1 3 2 Ling 3 1 2 Dass 1 2 3 Total 8 11 11
One-Sample Test (contd. ) Friedman Test: tests for equal preferences for something of various characteristics. l Example. Buyers’ rank of preference for three condominium types A, B, C. l Hypothesis: Buyers’ preferences for all condo type do not differ l Resp. Type A Type B Type C Man 2 3 1 Min 1 2 3 Lee 1 3 2 Ling 3 1 2 Dass 1 2 3 Total 8 11 11
 One-Sample Test (contd. ) l Test statistics: (n-1)k k Fr = ----- Rj 2 – 3 n(k+1) nk(k+1) j=1 where n = sample size, k = number of categories; R = is column’s total l For large n and k, Fr follows X 2(k-1); α
One-Sample Test (contd. ) l Test statistics: (n-1)k k Fr = ----- Rj 2 – 3 n(k+1) nk(k+1) j=1 where n = sample size, k = number of categories; R = is column’s total l For large n and k, Fr follows X 2(k-1); α
![One-Sample Test (contd. ) l l (5 -1)3 F = ------ [82 + 112] One-Sample Test (contd. ) l l (5 -1)3 F = ------ [82 + 112]](https://present5.com/presentation/b4821996958d29c891a0054f9bc35d32/image-8.jpg) One-Sample Test (contd. ) l l (5 -1)3 F = ------ [82 + 112] – 3 x 5(3+1) 5 x 3(3+1) = 1. 2 l X 2(3 -1); 0. 05 = 5. 99 l Ho not rejected. Buyers do not show different preference for condo type
One-Sample Test (contd. ) l l (5 -1)3 F = ------ [82 + 112] – 3 x 5(3+1) 5 x 3(3+1) = 1. 2 l X 2(3 -1); 0. 05 = 5. 99 l Ho not rejected. Buyers do not show different preference for condo type
 One-Sample Test (contd. ) Repeated measures ANOVA: tests outcome of a phenomenon under different conditions. l Example. Waiting time at junctions in the city area to determine level of congestion at different times of the day. l Test statistics: t/(m-1) F = --------r/[(n-1)(m-1) l where t = sum of squares due to treatment, r =sum of squares of residual, m = number of treatment, n = number of observations. l Critical region based on: F v 1. v 2; α where v 1 = (m-1), v 2 = (n-1)(m-1)
One-Sample Test (contd. ) Repeated measures ANOVA: tests outcome of a phenomenon under different conditions. l Example. Waiting time at junctions in the city area to determine level of congestion at different times of the day. l Test statistics: t/(m-1) F = --------r/[(n-1)(m-1) l where t = sum of squares due to treatment, r =sum of squares of residual, m = number of treatment, n = number of observations. l Critical region based on: F v 1. v 2; α where v 1 = (m-1), v 2 = (n-1)(m-1)
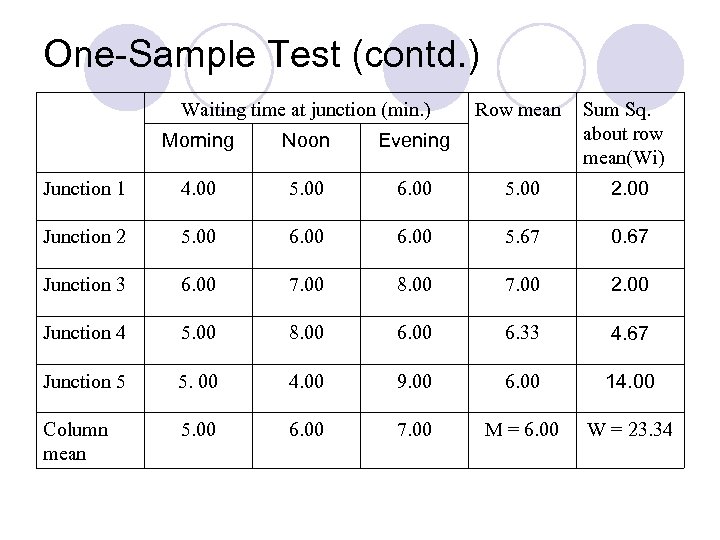 One-Sample Test (contd. ) Waiting time at junction (min. ) Row mean Sum Sq. about row mean(Wi) Morning Noon Evening Junction 1 4. 00 5. 00 6. 00 5. 00 2. 00 Junction 2 5. 00 6. 00 5. 67 0. 67 Junction 3 6. 00 7. 00 8. 00 7. 00 2. 00 Junction 4 5. 00 8. 00 6. 33 4. 67 Junction 5 5. 00 4. 00 9. 00 6. 00 14. 00 Column mean 5. 00 6. 00 7. 00 M = 6. 00 W = 23. 34
One-Sample Test (contd. ) Waiting time at junction (min. ) Row mean Sum Sq. about row mean(Wi) Morning Noon Evening Junction 1 4. 00 5. 00 6. 00 5. 00 2. 00 Junction 2 5. 00 6. 00 5. 67 0. 67 Junction 3 6. 00 7. 00 8. 00 7. 00 2. 00 Junction 4 5. 00 8. 00 6. 33 4. 67 Junction 5 5. 00 4. 00 9. 00 6. 00 14. 00 Column mean 5. 00 6. 00 7. 00 M = 6. 00 W = 23. 34
 One-sample test (contd. ) m n l. T l = (cij – M)2 i=1 j=1 = 30 l Wi = (cij – )2 l = 23. 34 l B = m ( - M)2 l = 6. 65 l t = n ( - M)2 = 10 W=t+r r=W–t = 23. 34 – 10 = 13. 34
One-sample test (contd. ) m n l. T l = (cij – M)2 i=1 j=1 = 30 l Wi = (cij – )2 l = 23. 34 l B = m ( - M)2 l = 6. 65 l t = n ( - M)2 = 10 W=t+r r=W–t = 23. 34 – 10 = 13. 34
 One-Sample Test (contd. ) 10/(3 -1) l Fc = ----------- = 2. 99 l 13. 34/(5 -1)(3 -2) l l Ft (3 -1), (3 -1)(5 -1); 0. 05 = 4. 46 l Ho not rejected. Congestion is quite the same at all times during the day.
One-Sample Test (contd. ) 10/(3 -1) l Fc = ----------- = 2. 99 l 13. 34/(5 -1)(3 -2) l l Ft (3 -1), (3 -1)(5 -1); 0. 05 = 4. 46 l Ho not rejected. Congestion is quite the same at all times during the day.
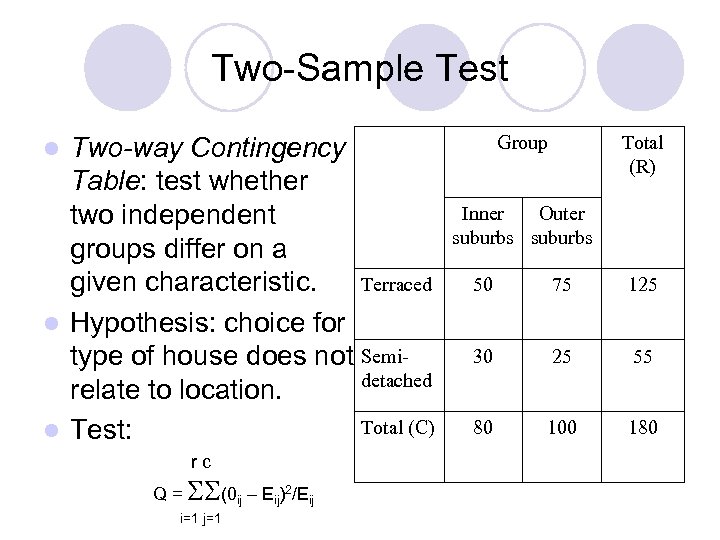 Two-Sample Test Two-way Contingency Table: test whether two independent groups differ on a Terraced given characteristic. l Hypothesis: choice for type of house does not Semidetached relate to location. Total (C) l Test: Group l rc Q = (0 ij – Eij)2/Eij i=1 j=1 Total (R) Inner Outer suburbs 50 75 125 30 25 55 80 100 180
Two-Sample Test Two-way Contingency Table: test whether two independent groups differ on a Terraced given characteristic. l Hypothesis: choice for type of house does not Semidetached relate to location. Total (C) l Test: Group l rc Q = (0 ij – Eij)2/Eij i=1 j=1 Total (R) Inner Outer suburbs 50 75 125 30 25 55 80 100 180
 Two-Sample Test (contd. ) D. o. f. = (r-1)(c-1), l where r=number of l rows, c=number of columns l l Eij = Ri. Cj/N Inner suburbs Outer suburbs Terraced 125 x 80/180 = 55. 6 125 x 100/180 = 69. 4 Semidetached 55 x 80/180 = 55 x 100/180 24. 4 = 30. 6 Q = (50 -55. 6)2/55. 6 + (30 -24. 4)2/24. 4 + (75 -69. 4)2/69. 4 + (25 -30. 6)2/30. 6 = 3. 33 (2 -1); 0. 05 = 3. 84 Ho not rejected
Two-Sample Test (contd. ) D. o. f. = (r-1)(c-1), l where r=number of l rows, c=number of columns l l Eij = Ri. Cj/N Inner suburbs Outer suburbs Terraced 125 x 80/180 = 55. 6 125 x 100/180 = 69. 4 Semidetached 55 x 80/180 = 55 x 100/180 24. 4 = 30. 6 Q = (50 -55. 6)2/55. 6 + (30 -24. 4)2/24. 4 + (75 -69. 4)2/69. 4 + (25 -30. 6)2/30. 6 = 3. 33 (2 -1); 0. 05 = 3. 84 Ho not rejected
 K Independent Test - Correlation “Co-exist”. E. g. * left shoe & right shoe, sleep & lying down, food & drink l Indicate “some” co-existence relationship. E. g. * Linearly associated (-ve or +ve) Formula: * Co-dependent, independent l But, nothing to do with C-A-E r/ship! l Example: After a field survey, you have the following data on the distance to work and distance to the city of residents in J. B. area. Interpret the results?
K Independent Test - Correlation “Co-exist”. E. g. * left shoe & right shoe, sleep & lying down, food & drink l Indicate “some” co-existence relationship. E. g. * Linearly associated (-ve or +ve) Formula: * Co-dependent, independent l But, nothing to do with C-A-E r/ship! l Example: After a field survey, you have the following data on the distance to work and distance to the city of residents in J. B. area. Interpret the results?
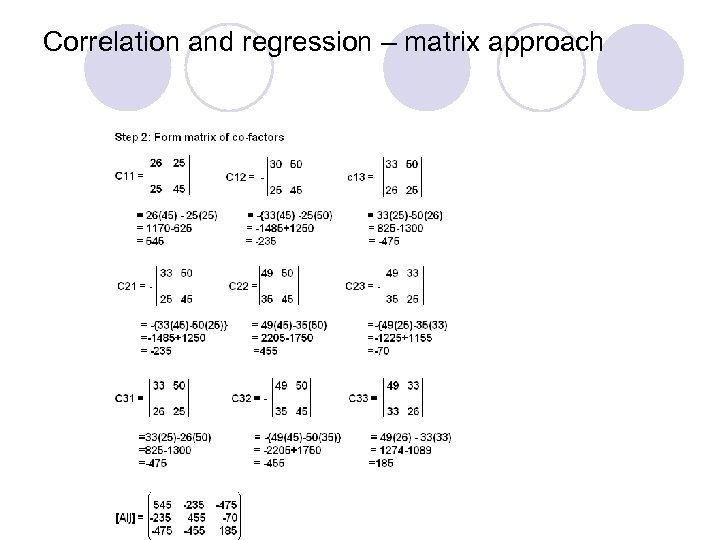
 K Independent Test - Correlation and regression – matrix approach
K Independent Test - Correlation and regression – matrix approach
 Correlation and regression – matrix approach
Correlation and regression – matrix approach
 Correlation and regression – matrix approach
Correlation and regression – matrix approach
 Correlation and regression – matrix approach
Correlation and regression – matrix approach
 Correlation and regression – matrix approach
Correlation and regression – matrix approach
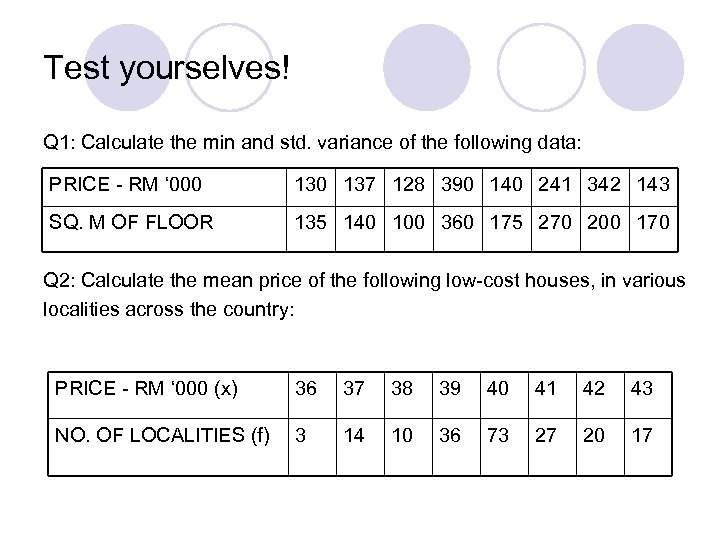 Test yourselves! Q 1: Calculate the min and std. variance of the following data: PRICE - RM ‘ 000 137 128 390 140 241 342 143 SQ. M OF FLOOR 135 140 100 360 175 270 200 170 Q 2: Calculate the mean price of the following low-cost houses, in various localities across the country: PRICE - RM ‘ 000 (x) 36 37 38 39 40 41 42 43 NO. OF LOCALITIES (f) 3 14 10 36 73 27 20 17
Test yourselves! Q 1: Calculate the min and std. variance of the following data: PRICE - RM ‘ 000 137 128 390 140 241 342 143 SQ. M OF FLOOR 135 140 100 360 175 270 200 170 Q 2: Calculate the mean price of the following low-cost houses, in various localities across the country: PRICE - RM ‘ 000 (x) 36 37 38 39 40 41 42 43 NO. OF LOCALITIES (f) 3 14 10 36 73 27 20 17
 Test yourselves! Q 3: From a sample information, a population of housing estate is believed have a “normal” distribution of X ~ (155, 45). What is the general adjustment to obtain a Standard Normal Distribution of this population? Q 4: Consider the following ROI for two types of investment: A: 3. 6, 4. 6, 5. 2, 4. 2, 6. 5 B: 3. 3, 3. 4, 4. 2, 5. 5, 5. 8, 6. 8 Decide which investment you would choose.
Test yourselves! Q 3: From a sample information, a population of housing estate is believed have a “normal” distribution of X ~ (155, 45). What is the general adjustment to obtain a Standard Normal Distribution of this population? Q 4: Consider the following ROI for two types of investment: A: 3. 6, 4. 6, 5. 2, 4. 2, 6. 5 B: 3. 3, 3. 4, 4. 2, 5. 5, 5. 8, 6. 8 Decide which investment you would choose.
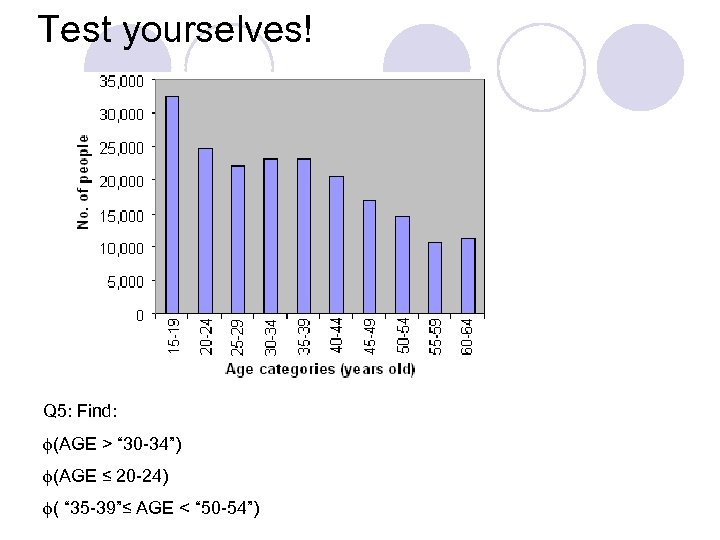 Test yourselves! Q 5: Find: (AGE > “ 30 -34”) (AGE ≤ 20 -24) ( “ 35 -39”≤ AGE < “ 50 -54”)
Test yourselves! Q 5: Find: (AGE > “ 30 -34”) (AGE ≤ 20 -24) ( “ 35 -39”≤ AGE < “ 50 -54”)
 Test yourselves! Q 6: You are asked by a property marketing manager to ascertain whether or not distance to work and distance to the city are “equally” important factors influencing people’s choice of house location. You are given the following data for the purpose of testing: Explore the data as follows: • Create histograms for both distances. Comment on the shape of the histograms. What is you conclusion? • Construct scatter diagram of both distances. Comment on the output. • Explore the data and give some analysis. • Set a hypothesis that means of both distances are the same. Make your conclusion.
Test yourselves! Q 6: You are asked by a property marketing manager to ascertain whether or not distance to work and distance to the city are “equally” important factors influencing people’s choice of house location. You are given the following data for the purpose of testing: Explore the data as follows: • Create histograms for both distances. Comment on the shape of the histograms. What is you conclusion? • Construct scatter diagram of both distances. Comment on the output. • Explore the data and give some analysis. • Set a hypothesis that means of both distances are the same. Make your conclusion.
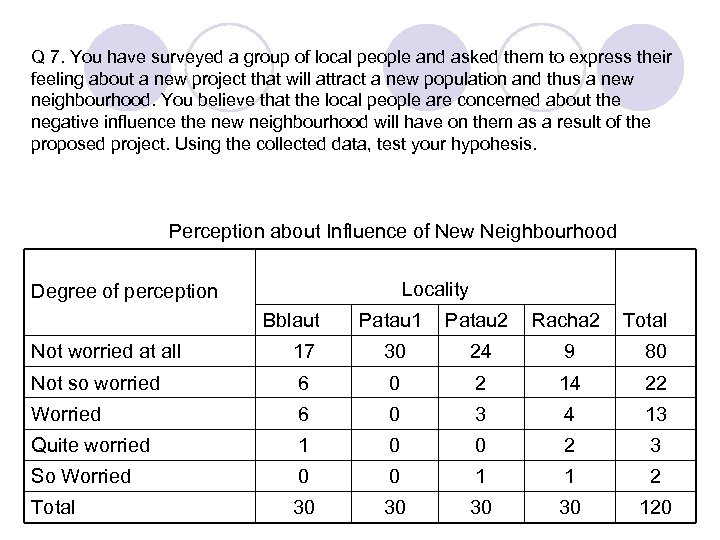 Q 7. You have surveyed a group of local people and asked them to express their feeling about a new project that will attract a new population and thus a new neighbourhood. You believe that the local people are concerned about the negative influence the new neighbourhood will have on them as a result of the proposed project. Using the collected data, test your hypohesis. Perception about Influence of New Neighbourhood Locality Degree of perception Bblaut Patau 1 Patau 2 Racha 2 Total Not worried at all 17 30 24 9 80 Not so worried 6 0 2 14 22 Worried 6 0 3 4 13 Quite worried 1 0 0 2 3 So Worried 0 0 1 1 2 Total 30 30 120
Q 7. You have surveyed a group of local people and asked them to express their feeling about a new project that will attract a new population and thus a new neighbourhood. You believe that the local people are concerned about the negative influence the new neighbourhood will have on them as a result of the proposed project. Using the collected data, test your hypohesis. Perception about Influence of New Neighbourhood Locality Degree of perception Bblaut Patau 1 Patau 2 Racha 2 Total Not worried at all 17 30 24 9 80 Not so worried 6 0 2 14 22 Worried 6 0 3 4 13 Quite worried 1 0 0 2 3 So Worried 0 0 1 1 2 Total 30 30 120
 Test yourselves! (contd. ) Q 7: From your initial investigation, you belief that tenants of “low-quality” housing choose to rent particular flat units just to find shelters. In this context , these groups of people do not pay much attention to pertinent aspects of “quality life” such as accessibility, good surrounding, security, and physical facilities in the living areas. Set your research design and data analysis procedure to address the research issue (b) Test your hypothesis that low-income tenants do not perceive “quality life” to be important in paying their house rentals. (a)
Test yourselves! (contd. ) Q 7: From your initial investigation, you belief that tenants of “low-quality” housing choose to rent particular flat units just to find shelters. In this context , these groups of people do not pay much attention to pertinent aspects of “quality life” such as accessibility, good surrounding, security, and physical facilities in the living areas. Set your research design and data analysis procedure to address the research issue (b) Test your hypothesis that low-income tenants do not perceive “quality life” to be important in paying their house rentals. (a)


