7befa61427197f51688d564b70924811.ppt
- Количество слайдов: 24
 Solving Systems with Inverse Matrices Lesson 6. 3
Solving Systems with Inverse Matrices Lesson 6. 3
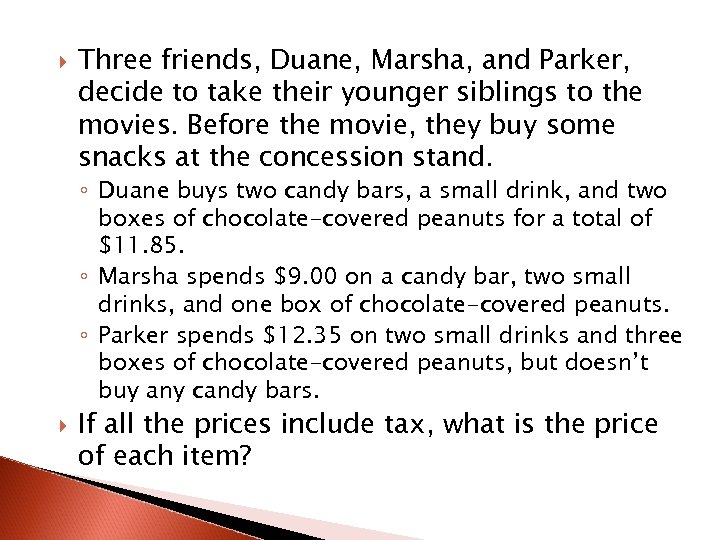 Three friends, Duane, Marsha, and Parker, decide to take their younger siblings to the movies. Before the movie, they buy some snacks at the concession stand. ◦ Duane buys two candy bars, a small drink, and two boxes of chocolate-covered peanuts for a total of $11. 85. ◦ Marsha spends $9. 00 on a candy bar, two small drinks, and one box of chocolate-covered peanuts. ◦ Parker spends $12. 35 on two small drinks and three boxes of chocolate-covered peanuts, but doesn’t buy any candy bars. If all the prices include tax, what is the price of each item?
Three friends, Duane, Marsha, and Parker, decide to take their younger siblings to the movies. Before the movie, they buy some snacks at the concession stand. ◦ Duane buys two candy bars, a small drink, and two boxes of chocolate-covered peanuts for a total of $11. 85. ◦ Marsha spends $9. 00 on a candy bar, two small drinks, and one box of chocolate-covered peanuts. ◦ Parker spends $12. 35 on two small drinks and three boxes of chocolate-covered peanuts, but doesn’t buy any candy bars. If all the prices include tax, what is the price of each item?
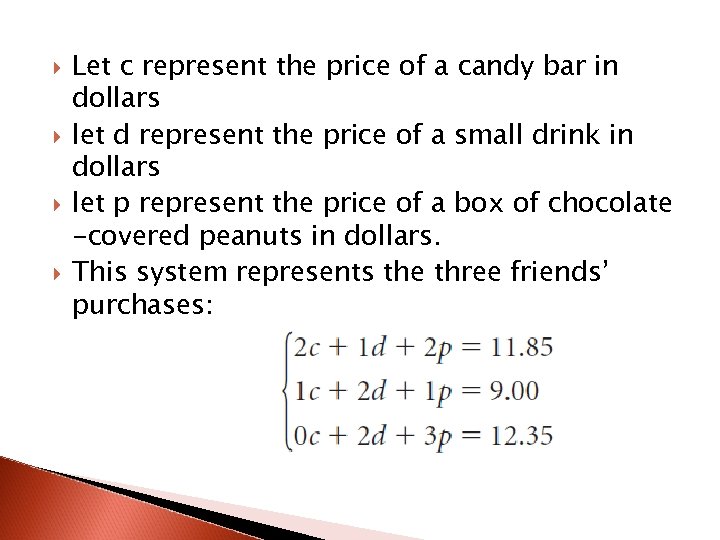 Let c represent the price of a candy bar in dollars let d represent the price of a small drink in dollars let p represent the price of a box of chocolate -covered peanuts in dollars. This system represents the three friends’ purchases:
Let c represent the price of a candy bar in dollars let d represent the price of a small drink in dollars let p represent the price of a box of chocolate -covered peanuts in dollars. This system represents the three friends’ purchases:
 To use matrices to solve this system first, translate these equations into a matrix equation in the form [A][X]=[B]
To use matrices to solve this system first, translate these equations into a matrix equation in the form [A][X]=[B]
![Solving this equation [A][X]=[B] is similar to solving the equation ax=b. We will Solving this equation [A][X]=[B] is similar to solving the equation ax=b. We will](https://present5.com/presentation/7befa61427197f51688d564b70924811/image-5.jpg) Solving this equation [A][X]=[B] is similar to solving the equation ax=b. We will multiply both sides by the inverse of a or a-1 Where [I] in an identity matrix and [A]-1 in an inverse matrix.
Solving this equation [A][X]=[B] is similar to solving the equation ax=b. We will multiply both sides by the inverse of a or a-1 Where [I] in an identity matrix and [A]-1 in an inverse matrix.
 What does a 2 by 2 identity matrix look like? Let’s find an identity matrix for An identity matrix for 2 matrix so that matrix will be another 2 x
What does a 2 by 2 identity matrix look like? Let’s find an identity matrix for An identity matrix for 2 matrix so that matrix will be another 2 x
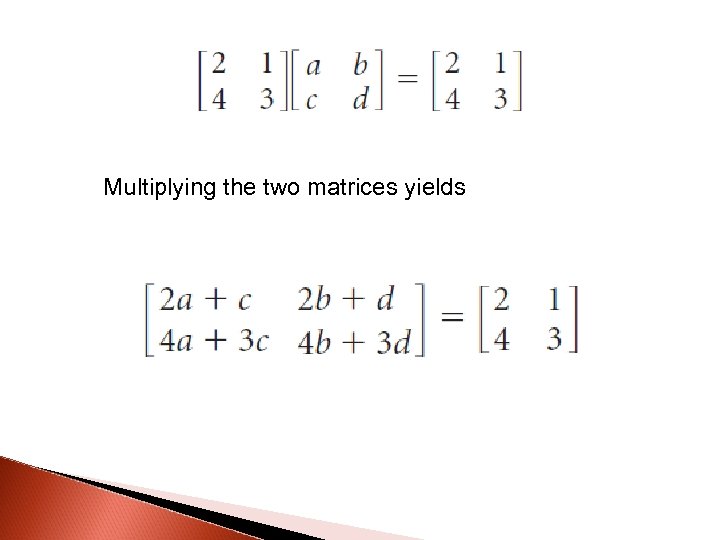 Multiplying the two matrices yields
Multiplying the two matrices yields
 Because the two matrices are equal, their entries must be equal. This yields: By using substitution and elimination you can find that a = 1, b = 0, c = 0, and d = 1. Therefore
Because the two matrices are equal, their entries must be equal. This yields: By using substitution and elimination you can find that a = 1, b = 0, c = 0, and d = 1. Therefore
 The 2 x 2 identity matrix is Can you see why multiplying this matrix by any 2 x 2 matrix results in the same 2 x 2 matrix?
The 2 x 2 identity matrix is Can you see why multiplying this matrix by any 2 x 2 matrix results in the same 2 x 2 matrix?
![Identity Matrix [I]: An identity matrix [I] is a square matrix that does not Identity Matrix [I]: An identity matrix [I] is a square matrix that does not](https://present5.com/presentation/7befa61427197f51688d564b70924811/image-10.jpg) Identity Matrix [I]: An identity matrix [I] is a square matrix that does not change another square matrix when multiplied. If [A] is a given square matrix then [I] is an identity matrix if
Identity Matrix [I]: An identity matrix [I] is a square matrix that does not change another square matrix when multiplied. If [A] is a given square matrix then [I] is an identity matrix if
![Inverse Matrix [A]-1 : If [A] is a square matrix then [A]-1 is the Inverse Matrix [A]-1 : If [A] is a square matrix then [A]-1 is the](https://present5.com/presentation/7befa61427197f51688d564b70924811/image-11.jpg) Inverse Matrix [A]-1 : If [A] is a square matrix then [A]-1 is the inverse matrix of [A] if Where [I] is an identity matrix.
Inverse Matrix [A]-1 : If [A] is a square matrix then [A]-1 is the inverse matrix of [A] if Where [I] is an identity matrix.
 Let’s find an Inverse Matrix In this investigation you will learn ways to find the inverse of a 2 x 2 matrix. Use the definition of an inverse matrix to set up a matrix equation. Use these matrices and the 2 x 2 identity matrix for [I].
Let’s find an Inverse Matrix In this investigation you will learn ways to find the inverse of a 2 x 2 matrix. Use the definition of an inverse matrix to set up a matrix equation. Use these matrices and the 2 x 2 identity matrix for [I].
![Use matrix multiplication to find the product [A][A]-1. Set that product equal to Use matrix multiplication to find the product [A][A]-1. Set that product equal to](https://present5.com/presentation/7befa61427197f51688d564b70924811/image-13.jpg) Use matrix multiplication to find the product [A][A]-1. Set that product equal to matrix [I].
Use matrix multiplication to find the product [A][A]-1. Set that product equal to matrix [I].
 Use the matrix equation from the previous step to write equations that you can solve to find values for a, b, c, and d. Solve the systems to find the values in the inverse matrix. 2 a+ c=1, 2 b +d=0, 4 a+ 3 c=0, 4 b+3 d =1; a =1. 5, b=0. 5, c=2, d=1;
Use the matrix equation from the previous step to write equations that you can solve to find values for a, b, c, and d. Solve the systems to find the values in the inverse matrix. 2 a+ c=1, 2 b +d=0, 4 a+ 3 c=0, 4 b+3 d =1; a =1. 5, b=0. 5, c=2, d=1;
![Use your calculator to find [A ]-1. If this answer does not match Use your calculator to find [A ]-1. If this answer does not match](https://present5.com/presentation/7befa61427197f51688d564b70924811/image-15.jpg) Use your calculator to find [A ]-1. If this answer does not match your answer to the last step, check your work for mistakes.
Use your calculator to find [A ]-1. If this answer does not match your answer to the last step, check your work for mistakes.
![Find the products of [A][A]-1 and [A]-1[A]. Do they both give you 1? Find the products of [A][A]-1 and [A]-1[A]. Do they both give you 1?](https://present5.com/presentation/7befa61427197f51688d564b70924811/image-16.jpg) Find the products of [A][A]-1 and [A]-1[A]. Do they both give you 1? Is matrix multiplication always commutative?
Find the products of [A][A]-1 and [A]-1[A]. Do they both give you 1? Is matrix multiplication always commutative?
 Not every square matrix has an inverse. Try to find the inverse of each of these matrices. Make a conjecture about what types of 2 x 2 square matrices do not have inverses. None of the matrices has an inverse. A 2 x 2 square matrix does not have an inverse when one row is a multiple of the other.
Not every square matrix has an inverse. Try to find the inverse of each of these matrices. Make a conjecture about what types of 2 x 2 square matrices do not have inverses. None of the matrices has an inverse. A 2 x 2 square matrix does not have an inverse when one row is a multiple of the other.
 Can a nonsquare matrix have an inverse? Why or why not? No. The product of a matrix and its inverse must be a square matrix because an identity matrix is always square and has the dimensions of the matrix and its inverse.
Can a nonsquare matrix have an inverse? Why or why not? No. The product of a matrix and its inverse must be a square matrix because an identity matrix is always square and has the dimensions of the matrix and its inverse.
 Example B Solve this system using an inverse matrix. First, rewrite the second equation in standard form.
Example B Solve this system using an inverse matrix. First, rewrite the second equation in standard form.
 The matrix equation for this system is If this equations corresponds with find [A]-1.
The matrix equation for this system is If this equations corresponds with find [A]-1.

 The solution to the system is (2, 1). Substitute the values into the original equations to check the solution.
The solution to the system is (2, 1). Substitute the values into the original equations to check the solution.
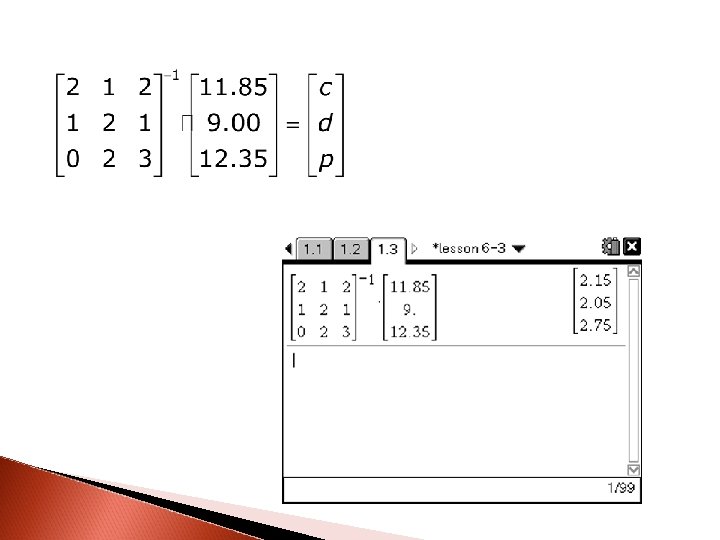
 Example C Use an inverse matrix to solve the problem posed at the beginning of the lesson. What is the cost of each snack item?
Example C Use an inverse matrix to solve the problem posed at the beginning of the lesson. What is the cost of each snack item?