Solving Linear Inequalities Warm Up Lesson Presentation Lesson

Solving Linear Inequalities Warm Up Lesson Presentation Lesson Quiz Holt Mc. Dougal. Algebra 1 Holt Algebra Holt Mc. Dougal 1 Algebra 1

Solving Linear Inequalities A linear inequality is similar to a linear equation, but the equal sign is replaced with an inequality symbol. A solution of a linear inequality is any ordered pair that makes the inequality true. Holt Mc. Dougal Algebra 1

Solving Linear Inequalities Example 1 A: Identifying Solutions of Inequalities Tell whether the ordered pair is a solution of the inequality. (– 2, 4); y < 2 x + 1 4 2(– 2) + 1 4 – 4 + 1 4 < – 3 (– 2, 4) is not a solution. Holt Mc. Dougal Algebra 1 Substitute (– 2, 4) for (x, y).

Solving Linear Inequalities Example 1 B: Identifying Solutions of Inequalities Tell whether the ordered pair is a solution of the inequality. (3, 1); y > x – 4 y>x− 4 1 3– 4 1> – 1 Substitute (3, 1) for (x, y). (3, 1) is a solution. Holt Mc. Dougal Algebra 1

Solving Linear Inequalities Check It Out! Example 1 Tell whether the ordered pair is a solution of the inequality. a. (4, 5); y < x + 1 b. (1, 1); y > x – 7 yx– 7 1 1– 7 1 > – 6 5 4+1 5 < 5 Substitute (4, 5) for (x, y). (4, 5) is not a solution. Holt Mc. Dougal Algebra 1 Substitute (1, 1) for (x, y). (1, 1) is a solution.

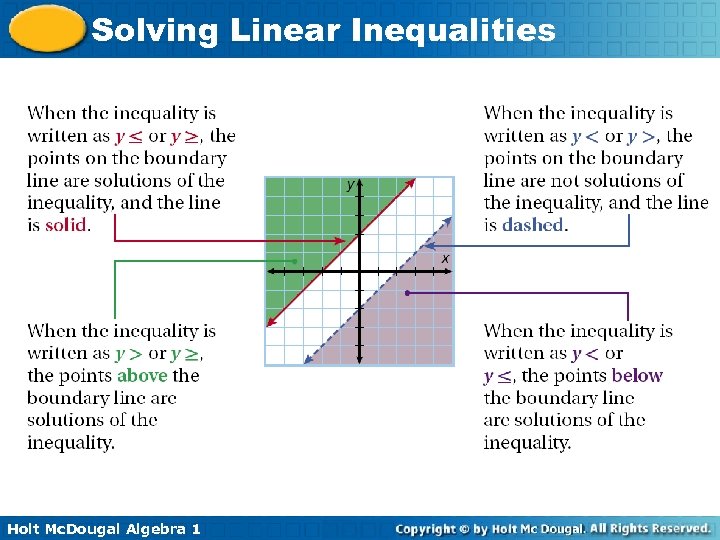Solving Linear Inequalities Holt Mc. Dougal Algebra 1

Solving Linear Inequalities Graphing Linear Inequalities Step 1 Solve the inequality for y (slopeintercept form). Step 2 Graph the boundary line. Use a solid line for ≤ or ≥. Use a dashed line for < or >. Shade the half-plane above the line for y > Step 3 or ≥. Shade the half-plane below the line for y < or y ≤. Check your answer. Holt Mc. Dougal Algebra 1

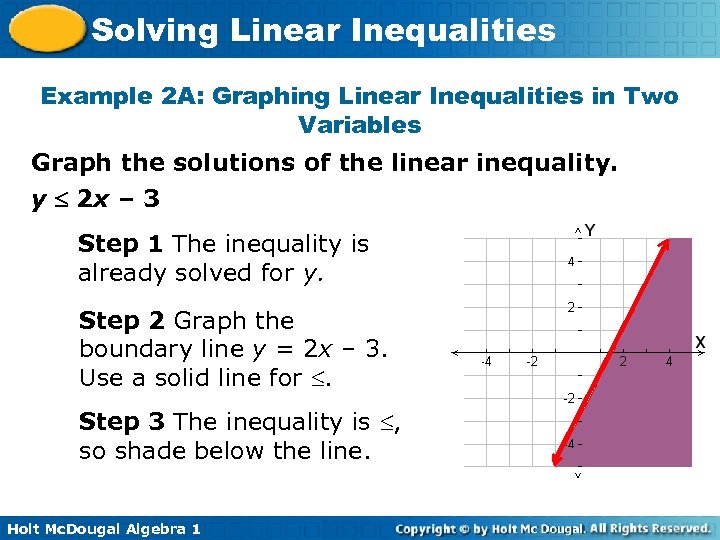Solving Linear Inequalities Example 2 A: Graphing Linear Inequalities in Two Variables Graph the solutions of the linear inequality. y 2 x – 3 Step 1 The inequality is already solved for y. Step 2 Graph the boundary line y = 2 x – 3. Use a solid line for . Step 3 The inequality is , so shade below the line. Holt Mc. Dougal Algebra 1

Solving Linear Inequalities Helpful Hint The point (0, 0) is a good test point to use if it does not lie on the boundary line. Holt Mc. Dougal Algebra 1

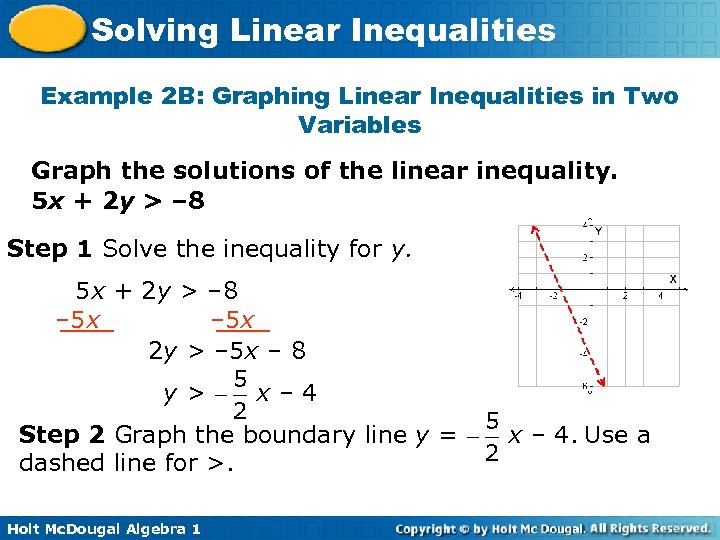Solving Linear Inequalities Example 2 B: Graphing Linear Inequalities in Two Variables Graph the solutions of the linear inequality. 5 x + 2 y > – 8 Step 1 Solve the inequality for y. 5 x + 2 y > – 8 – 5 x 2 y > – 5 x – 8 y> x– 4 Step 2 Graph the boundary line y = dashed line for >. Holt Mc. Dougal Algebra 1 x – 4. Use a

Solving Linear Inequalities Example 2 C: Graphing Linear Inequalities in two Variables Graph the solutions of the linear inequality. 4 x – y + 2 ≤ 0 Step 1 Solve the inequality for y. 4 x – y + 2 ≤ 0 –y ≤ – 4 x – 2 – 1 y ≥ 4 x + 2 Step 2 Graph the boundary line y ≥= 4 x + 2. Use a solid line for ≥. Holt Mc. Dougal Algebra 1

Solving Linear Inequalities Check It Out! Example 2 a Graph the solutions of the linear inequality. 4 x – 3 y > 12 Step 1 Solve the inequality for y. 4 x – 3 y > 12 – 4 x – 3 y > – 4 x + 12 y< – 4 Step 2 Graph the boundary line y = Use a dashed line for <. Holt Mc. Dougal Algebra 1 – 4.

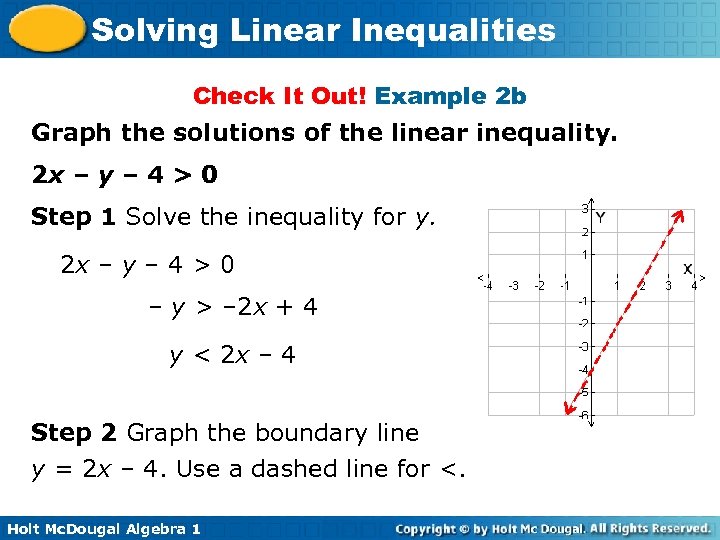Solving Linear Inequalities Check It Out! Example 2 b Graph the solutions of the linear inequality. 2 x – y – 4 > 0 Step 1 Solve the inequality for y. 2 x – y – 4 > 0 – y > – 2 x + 4 y < 2 x – 4 Step 2 Graph the boundary line y = 2 x – 4. Use a dashed line for <. Holt Mc. Dougal Algebra 1

Solving Linear Inequalities Check It Out! Example 2 c Graph the solutions of the linear inequality. Step 1 The inequality is already solved for y. Step 2 Graph the boundary = line . Use a solid line for ≥. Step 3 The inequality is ≥, so shade above the line. Holt Mc. Dougal Algebra 1

Solving Linear Inequalities Example 3: Application Ada has at most 285 beads to make jewelry. A necklace requires 40 beads, and a bracelet requires 15 beads. Write a linear inequality to describe the situation. Let x represent the number of necklaces and y the number of bracelets. Write an inequality. Use ≤ for “at most. ” Holt Mc. Dougal Algebra 1

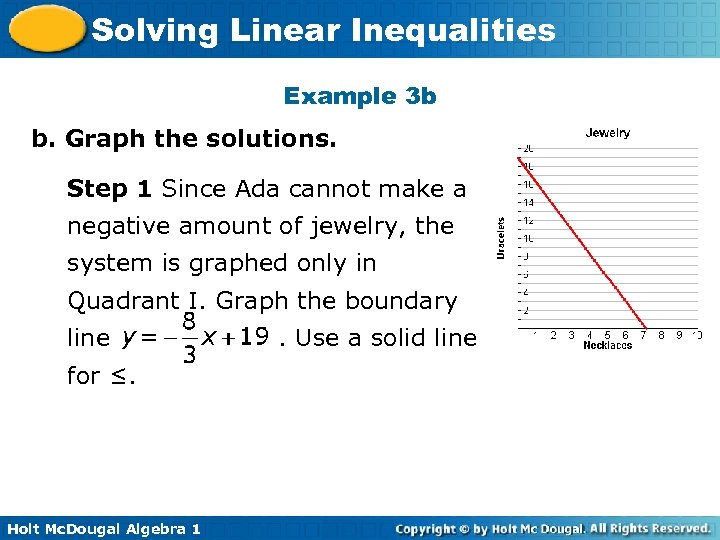Solving Linear Inequalities Example 3 b b. Graph the solutions. Step 1 Since Ada cannot make a negative amount of jewelry, the system is graphed only in Quadrant I. Graph the boundary line = for ≤. Holt Mc. Dougal Algebra 1 . Use a solid line

Solving Linear Inequalities Example 3 c c. Give two combinations of necklaces and bracelets that Ada could make. Two different combinations of jewelry that Ada could make with 285 beads could be 2 necklaces and 8 bracelets or 5 necklaces and 3 bracelets. (2, 8) (5, 3) Holt Mc. Dougal Algebra 1

Solving Linear Inequalities Check It Out! Example 3 What if…? Dirk is going to bring two types of olives to the Honor Society induction and can spend no more than $6. Green olives cost $2 per pound and black olives cost $2. 50 per pound. a. Write a linear inequality to describe the situation. b. Graph the solutions. c. Give two combinations of olives that Dirk could buy. Holt Mc. Dougal Algebra 1

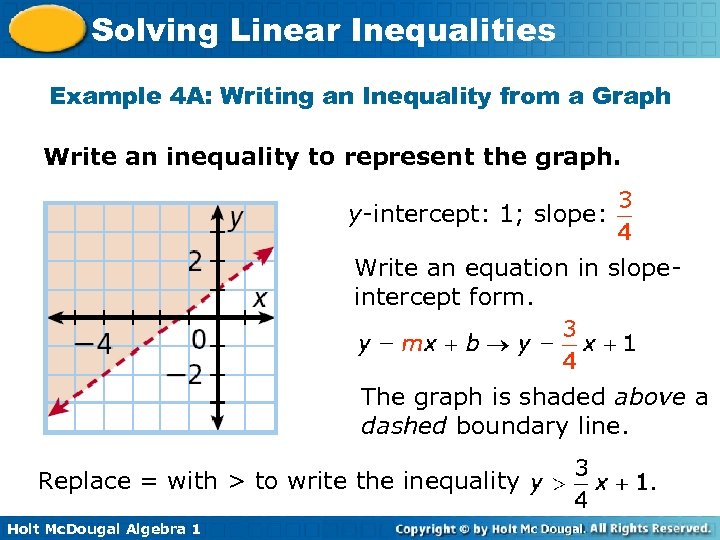Solving Linear Inequalities Example 4 A: Writing an Inequality from a Graph Write an inequality to represent the graph. y-intercept: 1; slope: Write an equation in slopeintercept form. The graph is shaded above a dashed boundary line. Replace = with > to write the inequality Holt Mc. Dougal Algebra 1

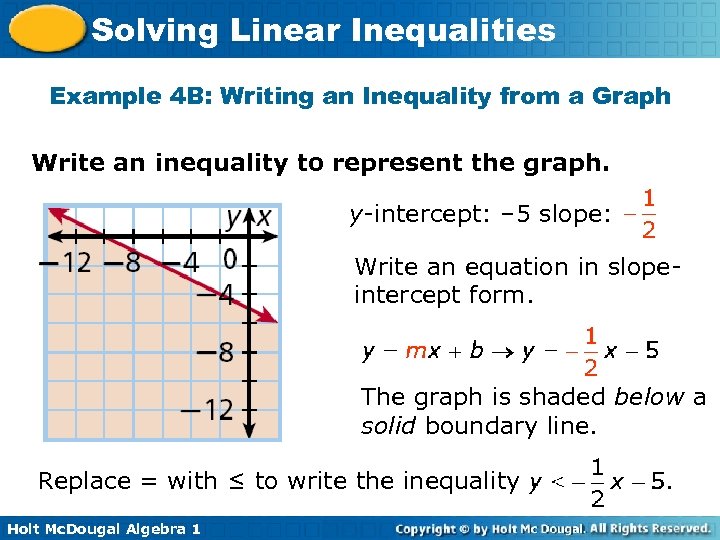Solving Linear Inequalities Example 4 B: Writing an Inequality from a Graph Write an inequality to represent the graph. y-intercept: – 5 slope: Write an equation in slopeintercept form. The graph is shaded below a solid boundary line. Replace = with ≤ to write the inequality Holt Mc. Dougal Algebra 1