Solvent Effects on Conical Intersections A Photochemical Analog

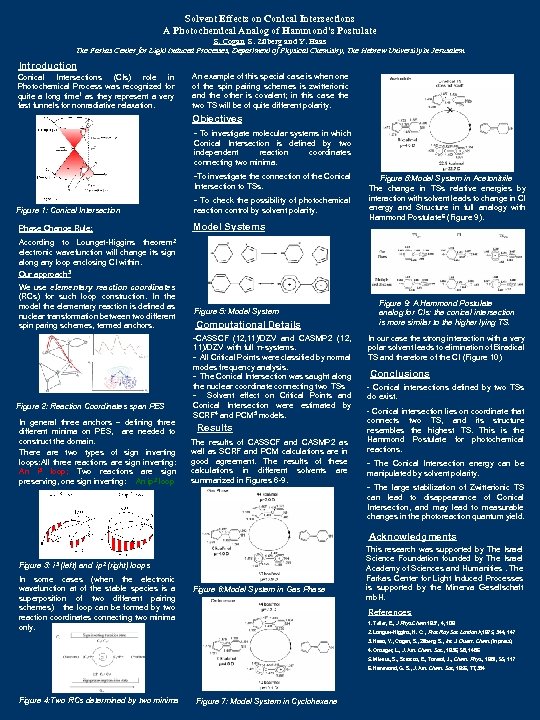Solvent Effects on Conical Intersections A Photochemical Analog of Hammond's Postulate S. Cogan, S. Zilberg and Y. Haas The Farkas Center for Light Induced Processes, Department of Physical Chemistry, The Hebrew University in Jerusalem Introduction Conical Intersections (CIs) role in Photochemical Process was recognized for quite a long time 1 as they represent a very fast funnels for nonradiative relaxation. An example of this special case is when one of the spin pairing schemes is zwitterionic and the other is covalent; in this case the two TS will be of quite different polarity. Objectives - To investigate molecular systems in which Conical Intersection is defined by two independent reaction coordinates connecting two minima. -To investigate the connection of the Conical Intersection to TSs. - To check the possibility of photochemical reaction control by solvent polarity. Figure 1: Conical Intersection Model Systems Phase Change Rule: Figure 8: Model System in Acetonitrile The change in TSs relative energies by interaction with solvent leads to change in CI energy and Structure in full analogy with Hammond Postulate 6 (Figure 9). theorem 2 According to Lounget-Higgins electronic wavefunction will change its sign along any loop enclosing CI within. Our approach 3 We use elementary reaction coordinates (RCs) for such loop construction. In the model the elementary reaction is defined as nuclear transformation between two different spin paring schemes, termed anchors. Figure 5: Model System Computational Details -CASSCF (12, 11)/DZV and CASMP 2 (12, Figure 2: Reaction Coordinates span PES In general three anchors – defining three different minima on PES, are needed to construct the domain. There are two types of sign inverting loops: All three reactions are sign inverting: An i 3 loop; Two reactions are sign preserving, one sign inverting: An ip 2 loop 11)/DZV with full π-systems. - All Critical Points were classified by normal modes frequency analysis. - The Conical Intersection was saught along the nuclear coordinate connecting two TSs - Solvent effect on Critical Points and Conical Intersection were estimated by SCRF 4 and PCM 5 models. Results The results of CASSCF and CASMP 2 as well as SCRF and PCM calculations are in good agreement. The results of these calculations in different solvents are summarized in Figures 6 -9. Figure 9: A Hammond Postulate analog for CIs: the conical intersection is more similar to the higher lying TS. In our case the strong interaction with a very polar solvent leads to elimination of Biradical TS and therefore of the CI (Figure 10) Conclusions - Conical intersections defined by two TSs do exist. - Conical intersection lies on coordinate that connects two TS, and its structure resembles the highest TS. This is the Hammond Postulate for photochemical reactions. - The Conical Intersection energy can be manipulated by solvent polarity. - The large stabilization of Zwitterionic TS can lead to disappearance of Conical Intersection, and may lead to measurable changes in the photoreaction quantum yield. Acknowledgments Figure 3: i 3 (left) and ip 2 (right) loops In some cases (when the electronic wavefunction at of the stable species is a superposition of two different pairing schemes) the loop can be formed by two reaction coordinates connecting two minima only. Figure 6: Model System in Gas Phase This research was supported by The Israel Science Foundation founded by The Israel Academy of Sciences and Humanities. The Farkas Center for Light Induced Processes is supported by the Minerva Gesellschaft mb. H. References 1. Teller, E. , J Phys Chem 1937, 4, 109 2. Longuet-Higgins, H. C. , Proc Roy Soc London A, 1975, 344, 147 3. Haas, Y. , Cogan, S. , Zilberg, S. , Int. J. Quant. Chem. (in press) 4. Onsager, L. , J. Am. Chem. Soc. , 1936, 58, 1486 5. Miertus, S. , Scrocco, E. , Tomasi, J. , Chem. Phys. , 1981, 55, 117 6. Hammond, G. S. , J. Am. Chem. Soc, 1955, 77, 334 Figure 4: Two RCs determined by two minima Figure 7: Model System in Cyclohexane