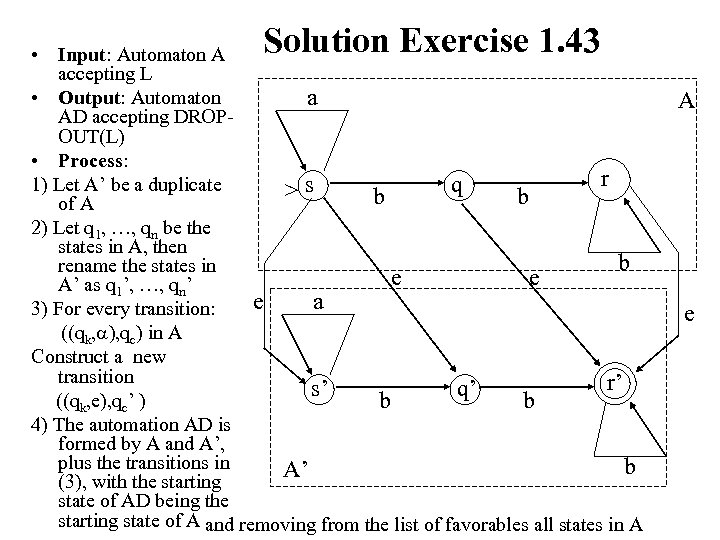
Solution Exercise 1 43 Input Automaton A

Solution Exercise 1. 43 • Input: Automaton A accepting L • Output: Automaton a AD accepting DROPOUT(L) • Process: r 1) Let A’ be a duplicate q >s b b of A 2) Let q 1, …, qn be the states in A, then b rename the states in e e A’ as q 1’, …, qn’ e a 3) For every transition: ((qk, ), qc) in A Construct a new transition r’ r s’ q’ q ((qk, e), qc’ ) b b 4) The automation AD is formed by A and A’, plus the transitions in b A’ (3), with the starting state of AD being the starting state of A and removing from the list of favorables all states in A A e

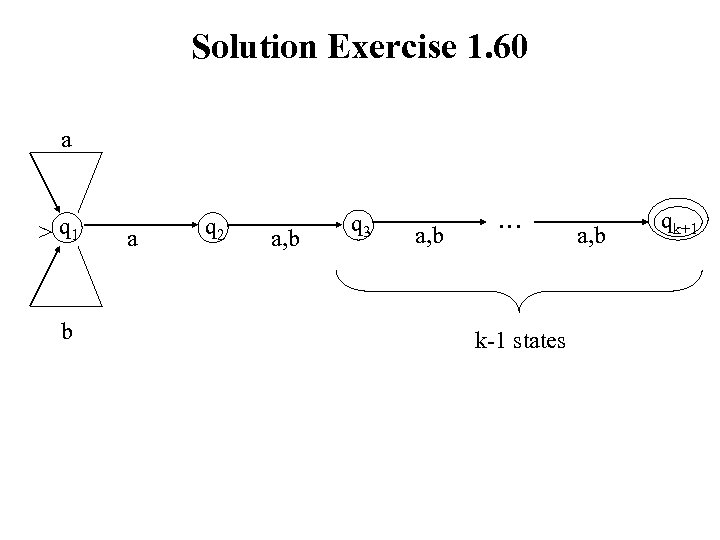Solution Exercise 1. 60 a > q 1 b a q 2 a, b q 3 a, b … k-1 states a, b qk+1

Nonregular Languages L = {akbk : k N} Lets show that is regular: • find a regular expression for L, or • automaton that accepts L How can we proof that L is nonregular?

Pumping Lemma (Theorem 1. 70) Lemma. Let L be a regular language. There exists an integer p > 0 such that for any string w L with |w| p, then there exist strings x, y, and z such that: • w = xyz • y e • |xy| p • xyiz L for i = 0, 1, 2, … y has at least 1 letter The substring xy contains at most the first p letters of w (and z contains the rest of letters) Pumping part: xz, xy 2 z, xy 10 z and any other string of the form xyiz must be in L

Sketch of Proof (1) Lets analyze how words are accepted by finite automata. Lets take a generic word: w = 1 2 … m If w is accepted by a DFA D. What does it mean: D: > s 1 1 s 2 2 … m Where each si are states in D sm

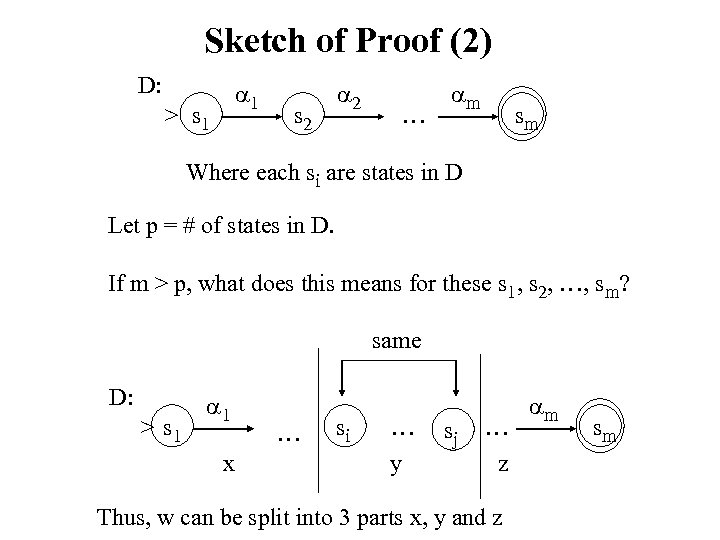Sketch of Proof (2) D: 1 > s 1 s 2 2 … m sm Where each si are states in D Let p = # of states in D. If m > p, what does this means for these s 1, s 2, …, sm? same D: > s 1 1 x … si … y sj … z Thus, w can be split into 3 parts x, y and z m sm

Exercises • Lets proof that L = {akbk : k N} is nonregular using the pumping lemma • Given a word w, w. R denotes the reverse of the word. Lets proof that Palindromes = {w * : w = w. R} is nonregular using the pumping lemma ( = {a, b}) • Note: In Example 1. 73 of the book (read it!) only case Number 1 is necessary to analyze. The other two cases cannot happen because |xy| p (the text below the cases states it so too but at least one of the selected answers to exercises again analyze more cases than it is necessarily -e. g. , Exercise 1. 29 (a) -)

Homework (Optional: Wednesday!) • Exercise 1. 29 (a), (b) • Problem 1. 46 (b) • Problem 1. 53 (Hint: you can pick any numbers x, y and z as long as: • x = y+z, and • Viewed as an string, x = y+z has at least p characters So what you are trying to do is to take some numbers x, y and z so when you “pump” the summation longer adds up)