Соловьёв Андрей

Особенности жидкости • • • 1. 2. 3. 4. 5. 6. Жидкость - вещество: - обладающее несжимаемостью, текучестью и подвижностью молекул; - способное изменять свою форму под воздействием внешних сил и температурных изменений. Особенности Сохранение объёма, но несохранение формы. Велики силы взаимодействия между частицами. Текучесть жидкостей. Частицы колеблются около одной точки, а потом совершают прыжки. Характерен ближний порядок. По свойствам и строению ближе к твёрдым телам.

Натяжение поверхностного слоя Сила R 1 -втягивает молекулу в жидкость. значит со стороны поверхностного слоя на жидкость создаётся молекулярное давление R 1 R 2=0 Епов=σS , где σ-коэффициент поверхностного натяжения Физический смысл σ: σ=Епов/S если S=1 m², то σ численно равно Епов. коэффициент поверхностного натяжения зависит: 1. от рода жидкости 2. от температуры 3. от среды над поверхностью

Силы поверхностного натяжения • Это силы обусловленные взаимодействием частиц жидкости, стремящиеся сократить площадь поверхности и направленные по касательной к этой поверхности. • A=ΔEпов=σ ∆S (1) • ΔS=2 Lh • A=2 Fпов h (2) (3) • (2)(3)в(1) 2 Fповh= σ 2 L h Fпов= σ L ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ S мыльной пленки в проволочной рамке TUV удерживает в равновесии свободно движущуюся проволочку PQ.

Явление смачивания и несмачивания • Краевой угол(θ)-это угол образованный плоской поверхностью твёрдого тела и плоскостью, касательной к свободной поверхности жидкости проходящей через границы трёх сред. θ θ Смачивание Не смачивание 0≤θ≥ 90 90≤θ≥ 180 Угол θ=0º -полное смачивание
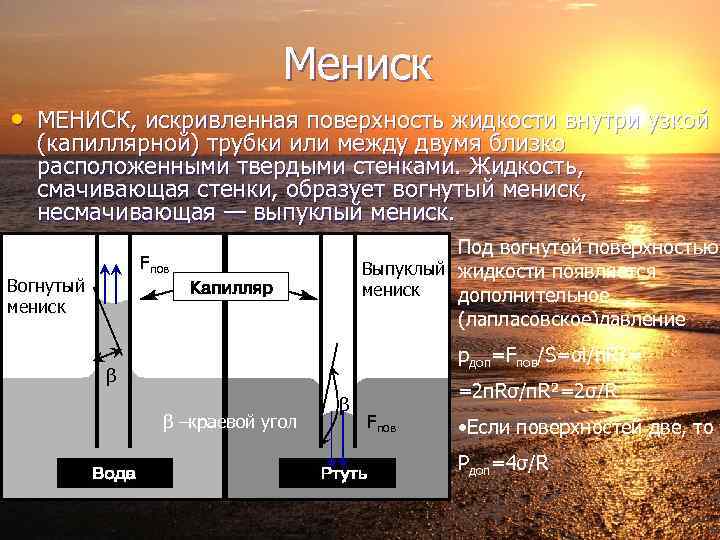
Мениск • МЕНИСК, искривленная поверхность жидкости внутри узкой (капиллярной) трубки или между двумя близко расположенными твердыми стенками. Жидкость, смачивающая стенки, образует вогнутый мениск, несмачивающая — выпуклый мениск. Под вогнутой поверхностью Выпуклый жидкости появляется мениск дополнительное (лапласовское)давление Fпов Вогнутый мениск pдоп=Fпов/S=σl/πR²= β β –краевой угол β =2πRσ/πR²=2σ/R Fпов • Если поверхностей две, то Pдоп=4σ/R

Капиллярные явления r F F Условие равновесия r Pдоп. =pгидростат. 2σ/R=ρgh H Жидкость смачивает стенки капилляра Жидкость не смачивает стенки капилляра Следовательно: h=2σ/ρg. R Капилляр-трубка с малым диаметром(r≈2 mm)

Капиллярные явления в быту и технике Влагообмен в почве и в растениях осуществляется за счёт поднятия воды по тончайшим капиллярам. Вода, находящаяся в почве, может проникать в стены здания по капиллярным каналам таких пористых строительных материалов, кирпич, известняк и др.

Задачи 1. Задача на силы поверхностного 2. 3. 4. натяжения. Задача на капиллярные явления. Задача на энергию поверхностного натяжения. Комбинированные задачи.

Задача № 1 • Мыльная вода вытекает из капилляра по каплям. В момент отрыва диаметр шейки капли равен d=1. 0 mm. Масса капли m=0. 0129 г. Найдите коэффициент поверхностного натяжения σ жидкости.

• Дано Решение: d=1. 0 mm запишем условие m=0. 0129 г равновесия: σ -? Fпов=mg(1) Fпов =σl σ= Fпов/l (2) l=2πR(3) R=d/2(4) (1)(3)(4)в(2) σ=mg/πd σ=4. 05*10 -2 Н/м Ответ: σ=4. 05*10 -2 Н/м

Задача № 2 • Оцените, сколько воды можно унести в решете. Ячейка решета представляет собой квадратик размера s=1*1 mm², площадь решета S=0. 1 m². Решето водой не смачивается.

• Дано: s=1*1 mm² Решение: n=S/s(1) , где n. S=0. 1 m² количество капелек воды M-? Вода не будет выливаться из решета, если равнодействующая сил поверхностного натяжения компенсирует силу тяжести. mg=Fпов (2) Fпов=σl (3)в(2)mg=σl mg=4σl m=4σl /g(4) l=√s (5)в(4) m=4σ√s /g(6) M=m n(7) (7)в(6) M= 4σ√s n /g с учётом(1) M= 4σS/g√s M=3 кг Ответ: M=3 кг

Задача № 3 • В одну большую каплю слились капель n=8 ртути радиусом r=1 mm каждая. Какое количество теплоты Q при этом выделится? Коэффициент поверхностного натяжения ртути σ =0. 41 Н/м

• Дано: n=8 Hg r=1 mm σ =0. 41 Н/м Q-? Решение: n r Q=Eпов 1 -Eпов 2 (1) Eпов 1= σs=4πr² σ n (2) Eпов 2=σS=4πR² σ (3) V 1=4/3 πr³ n (4) V 2=4/3 πR³ (5) так как объём постоянен (4)=(5) 4/3 πr³ n= 4/3 πR³ R=³√n r ³ =r ³√n (6) (2)(3)в(1) Q= 4πr² σ n - 4πR² σ (7) (6)в(7) Q= 4πr² σ (n- (³√n )²) Q= 4πr² σ (n-n 2/3) Q=20. 6 Дж Ответ: 20. 6 Дж R

Задача № 4 • Петлю из резинового шнура длиной L и поперечным сечением S положили на плёнку жидкости. Плёнку прокололи внутри петли, в результате чего она растянулась в окружность радиуса R. Полагая, что при малых растяжений для резины справедлив закон Гука и модуль Юнга для резины равен E, определите коэффициент поверхностного натяжения σ жидкости.

• Дано: L S R E Решение: y Fпов T x 2α T σ -? R Выберем малую часть резины и запишем для неё условие равновесия. Сила натяжения резины направлена по радиусу к окружности (касательной к плоской поверхности)

• Fпов =T+T проецируем на ось ординат: Fпов=2 Tsinα(1) Fпов = σl (2) l=2αR (3) (2)(3)d(1) σ2αR =2 Tsin α При малых углах sin α=α σ2αR=2 Tα σR =T σ=T/R (4) T=kx(5) закон Гука K=ES/L (6) x=2πR-L (7) (6)(7)в(5) T=ES/L (2πR-L) (8)в(4) σ=ES (2πR-L)/LR Ответ: σ=ES (2πR-L)/LR
А все кончается, кончается…