Сокращение дробей.pptx
- Количество слайдов: 9

Сокращение дробей

Основное свойство дроби Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь. 4 2∙ 2 2 = 4∙ 2 = 8 4 2 200 : 100 200 = 300 : 100 = 3 300 1 21 : 21 21 = 105 : 21 = 5 105

Сокращение дробей 333 777 5000 10000 = = 333 : 111 777 : 111 5000 : 5000 10000 : 5000 3 7 = = 1 2 Деление числителя и знаменателя дроби на одно и то же, не равное нулю, число, называется сокращением дроби.
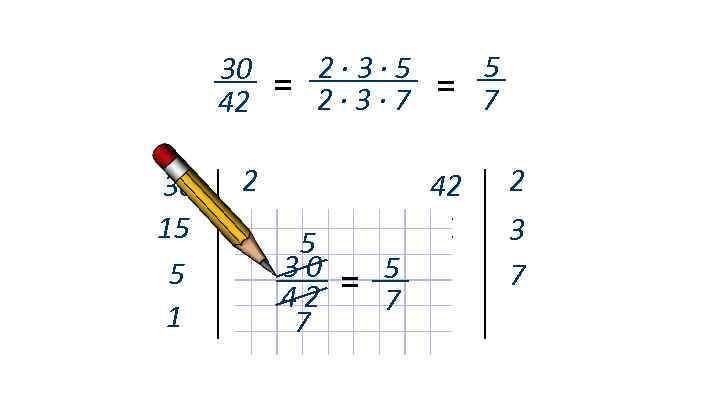
30 42 30 15 5 1 = 2∙ 3∙ 5 2∙ 3∙ 7 2 3 5 5 30 42 7 = = 42 21 5 7 7 1 5 7 2 3 7

4 15 несократимая дробь 6 простые числа 7 10 4 и 15 – взаимно 35 10 21 Сокращение дроби можно взаимно провести тогда и 6 и 35 – взаимно 7 и 10 – 10 и 21 – толькопростые числа тогда, когда её числитель числа простые и числа знаменатель не являются взаимно простыми числами.
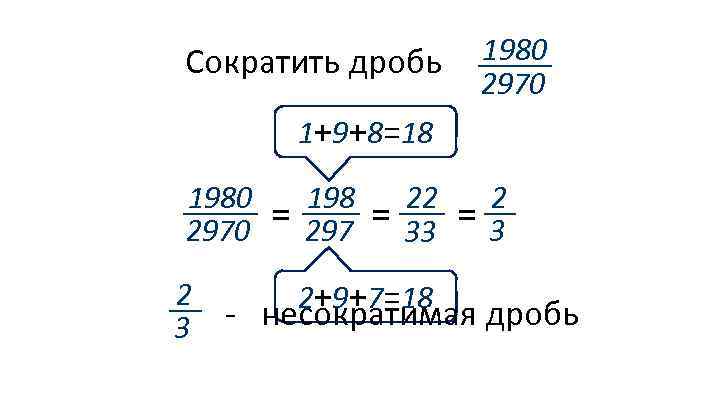
1980 2970 Сократить дробь 1+9+8=18 1980 2970 2 3 = 198 297 = 22 33 2+9+7=18 = 2 3 - несократимая дробь

36 126 Найдём НОД чисел 36 и 126. 36 2 126 2 18 63 2 3 ? 9 21 3 3 72 3 36 7 3 36 18 = 126 : : 18 = 7 1 126 1 НОД (36; 126) = 2 ∙ 3 = 18 Сократить дробь

Отметить на координатном луче 33 точку А ( 55 ). O 0 А 1 33 55 = 3 5

Деление числителя и знаменателя дроби на одно и то же число, не равное нулю, называется сокращением дроби. Если же числитель и знаменатель данной дроби взаимно просты, то дробь сократить нельзя. Такие дроби называются несократимыми дробями.
Сокращение дробей.pptx