00a3a8235817c4376b82ddd77b187a6d.ppt
- Количество слайдов: 33

Software Cybernetics: Progress and Challenges Aditya P. Mathur Professor, Department of Computer Science, Associate Dean, Graduate Education and International Programs Purdue University Monday December 20, 2004. University of Paderborn, Germany.
![Cybernetics [n] the field of science concerned with processes of communication and control (especially Cybernetics [n] the field of science concerned with processes of communication and control (especially](https://present5.com/presentation/00a3a8235817c4376b82ddd77b187a6d/image-2.jpg)
Cybernetics [n] the field of science concerned with processes of communication and control (especially the comparison of these processes in biological and artificial systems)
![Software Cybernetics [n] the field of science concerned with processes of communication and control Software Cybernetics [n] the field of science concerned with processes of communication and control](https://present5.com/presentation/00a3a8235817c4376b82ddd77b187a6d/image-3.jpg)
Software Cybernetics [n] the field of science concerned with processes of communication and control in software systems.

Sample Problems Control of the software test process: How much and what additional effort is to be applied to achieve the desired quality objective under time/cost constraints? Optimal selection of tests: What is an optimal set of tests for achieving the desired quality objective given time constraints?

Sample Problems (continued) Software performance control How best to adjust software parameters so that an optimal level of performance is maintained? Control of the software development process: What is an optimal set of process variables required to achieve delivery objectives within cost/time constraints?

Approaches 1. Use instinct and experience. 2. Use (1) supported by quantitative tools. (a) Use simulation: “forward” approach. (b) Use simulation: “forward” approach. (c) Use (a) plus feedback control: “inverse” approach. Software cybernetic approach. .

Closed Loop (feedback) Control Specifications Effort + Program Additional effort Required Quality Observed Quality - f(e) What is f ?
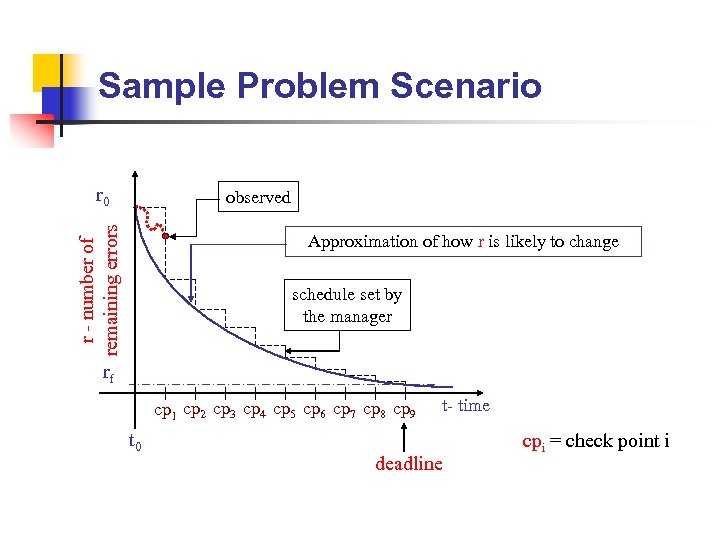
Sample Problem Scenario r 0 r - number of remaining errors observed Approximation of how r is likely to change schedule set by the manager rf cp 1 cp 2 cp 3 cp 4 cp 5 cp 6 cp 7 cp 8 cp 9 t 0 t- time deadline cpi = check point i
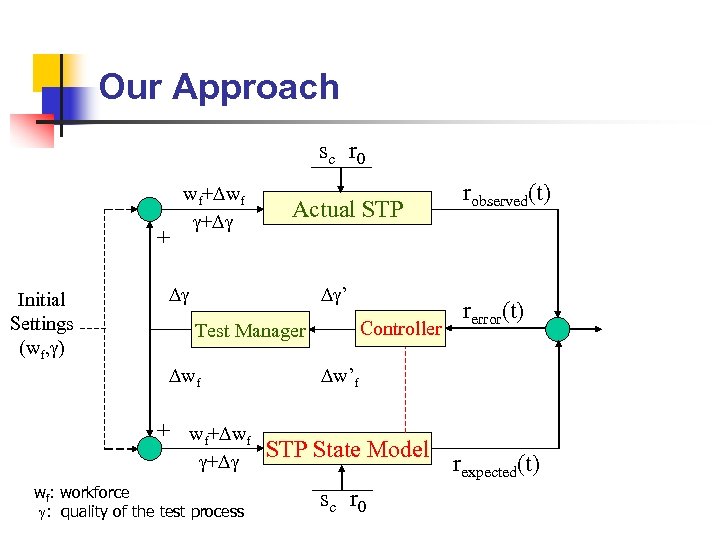
Our Approach s c r 0 + Initial Settings (wf, ) wf+ wf + Actual STP ’ Controller Test Manager wf + wf: workforce : quality of the test process robserved(t) rerror(t) w’f STP State Model s c r 0 rexpected(t)
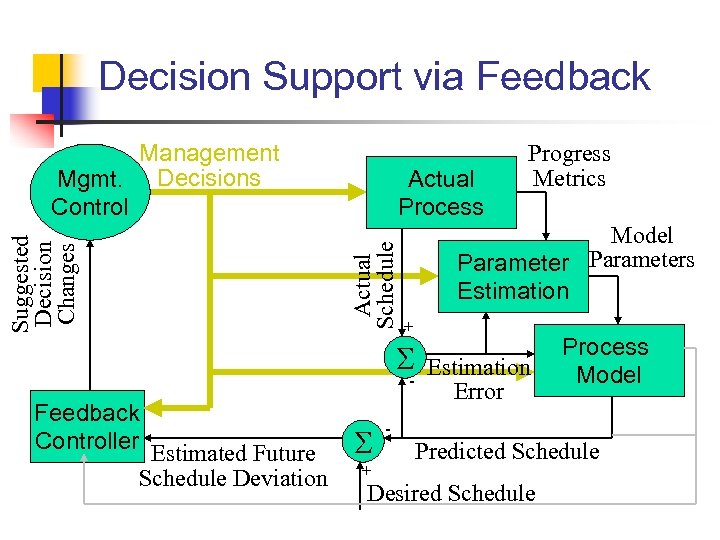
Decision Support via Feedback Actual Process Actual Schedule Suggested Decision Changes Management Mgmt. Decisions Control Model Parameters Estimation + - Feedback Controller Estimated Future Schedule Deviation + - Progress Metrics Estimation Error Process Model Predicted Schedule Desired Schedule

Challenges (Sources of difficulty) Physical Logical (software) Laws of physics Yes No Object controlled Physical Logical (and Humans) Time dependence Stationary and nonstationary Non-stationary Rate of change Very slow to very fast Slow Parameter variability Relatively low High

Overcoming the challenge: Understanding the problem n Partnership amongst researchers and practitioners. n Is the problem real? n Are the existing solutions adequate?

Overcoming the challenge: Solving the problem n Parternership amongst researchers and practitioners. n Develop realistic models n Develop parameter estimation methods. n Develop ways to incorporate parameter estimation into the development process.

Details and Case Studies n Razorfish n Guidant Corporation n Sun Microsystems

Physical and Software Systems: An Analogy External force To err is Human Dashpot Block Xcurrent Software X: Position Number of remaining errors Spring Xequilibrium Rigid surface Spring Force Effective Test Effort Mass of the block Software complexity Viscosity Quality of the test process
![Physical Systems: Laws of Motion [1] First Law: Every object in a state of Physical Systems: Laws of Motion [1] First Law: Every object in a state of](https://present5.com/presentation/00a3a8235817c4376b82ddd77b187a6d/image-16.jpg)
Physical Systems: Laws of Motion [1] First Law: Every object in a state of uniform motion tends to remain in that state of motion unless an external force is applied to it. Does not (seem to) apply to testing because the number of errors does not change when no external effort is applied to the application.
![Physical Systems: Laws of Motion [2] Newton’s Second Law: The relationship between an object's Physical Systems: Laws of Motion [2] Newton’s Second Law: The relationship between an object's](https://present5.com/presentation/00a3a8235817c4376b82ddd77b187a6d/image-17.jpg)
Physical Systems: Laws of Motion [2] Newton’s Second Law: The relationship between an object's mass m, its acceleration a, and the applied force F is F = ma. CDM First Postulate: The relationship between the complexity Sc of an application, its rate of reduction in the number of. . remaining errors, and the applied effort E is E=Sc r.
![Physical Systems: Laws of Motion [3] Third Law: For every action force, there is Physical Systems: Laws of Motion [3] Third Law: For every action force, there is](https://present5.com/presentation/00a3a8235817c4376b82ddd77b187a6d/image-18.jpg)
Physical Systems: Laws of Motion [3] Third Law: For every action force, there is an equal and opposite reaction force. When an effort is applied to test software, it leads to (mental) fatigue on the tester. Unable to quantify this relationship.

CDM First Postulate The magnitude of the rate of decrease of the remaining errors is directly proportional to the net applied effort and inversely proportional to the complexity of the program under test. This is analogous to Newton’s Second Law of motion.

CDM Second Postulate Analogy with the spring: The magnitude of the effective test effort is proportional to the product of the applied work force and the number of remaining errors. for an appropriate . Note: While keeping the effective test effort constant, a reduction in r requires an increase in workforce.

CDM Third Postulate Analogy with the dashpot: The error reduction resistance is proportional to the error reduction velocity and inversely proportional to the overall quality of the test phase. for an appropriate . Note: For a given quality of the test phase, a larger error reduction velocity leads to larger resistance.

State Model Force (effort) balance equation: : Disturbance. x(t) = Ax(t) + B u(t)

Computing the feedback: Question Given: r(T): the number of remaining errors at time T r(T+ T): the desired number of remaining errors at time T+ T Question: What changes to the process parameters will achieve the desired r(T+ T) ?

Computing the feedback: Answer From basic matrix theory: The largest eigenvalue of a linear system dominates the rate of convergence. Hence we need to adjust the largest eigenvalue of the system so that the response converges to the desired value within the remaining weeks ( T). This can be achieved by maintaining: Obtain the desired eigenvalue.

Computing the feedback-Calculations ( max) Given the constraint: Compute the desired max We know that the eigenvalues of our model are the roots of its characteristic polynomial of the A matrix.

Computing the feedback-Calculations ( max) We use the above equation to calculate the space of changes to wf and such that the system maintains its desired eigenvalue.

A Flow Model of Incremental Software Development/Test Specs Feat. Specs Test Authoring Test Code Coding Test Verification & Correction Reg. Cases Latent Defects Project Code Debugging Regression Testing Known Defects

Workforce Allocation n n Workforce allocated to particular tasks Effort is split across all active tasks
![State-Model [Example] Equations n System State n Progress n n n Feature Coding (fc) State-Model [Example] Equations n System State n Progress n n n Feature Coding (fc)](https://present5.com/presentation/00a3a8235817c4376b82ddd77b187a6d/image-29.jpg)
State-Model [Example] Equations n System State n Progress n n n Feature Coding (fc) Code Debugging (dr) Test Authoring (ta) Test Debugging (td) Regression Testing (rr) Defect Model n n Development Testing

Variable Productivity Equation n Human Productivity n Workload Dependent (Csikszentmihalyi, ’ 88) • rb – Base Work rate • wc – Current workload size • c – Fractional sizedependent increase • wn – Nominal workload size

The “Productivity” Eqns. n Process Productivity (E. g. Feature Coding) n Defect Introduction n Defect Detection (Cangussu et al. , ’ 02)

Control Strategy n Model Predictive Control

Model Predictive Control n Select Cost Functional n E. g. n n Q 1, Q 2 : = positive definite Calculate n where S[xk, uk, k+P] xpk, k+P
00a3a8235817c4376b82ddd77b187a6d.ppt