6e11e3e609d96fc0e5f7f9ac7eb2a8e6.ppt
- Количество слайдов: 65

Softimage ICE: Making Math Accessible Todd Akita PSYOP Inc. © 2012 Autodesk

Class Summary The goal of this course is to equip artists with the math we need to be more productive, and ultimately more creative. Custom solutions require problem-solving skills, and even rudimentary math is a powerful weapon to bring to the fight. © 2012 Autodesk

Learning Objectives At the end of this class, you will be able to: Use ICE to visualize basic math concepts Apply these math concepts to build functioning components from scratch Build larger compound tools from smaller components Deploy these tools to your team though a workgroup © 2012 Autodesk
Trigonometry © 2012 Autodesk
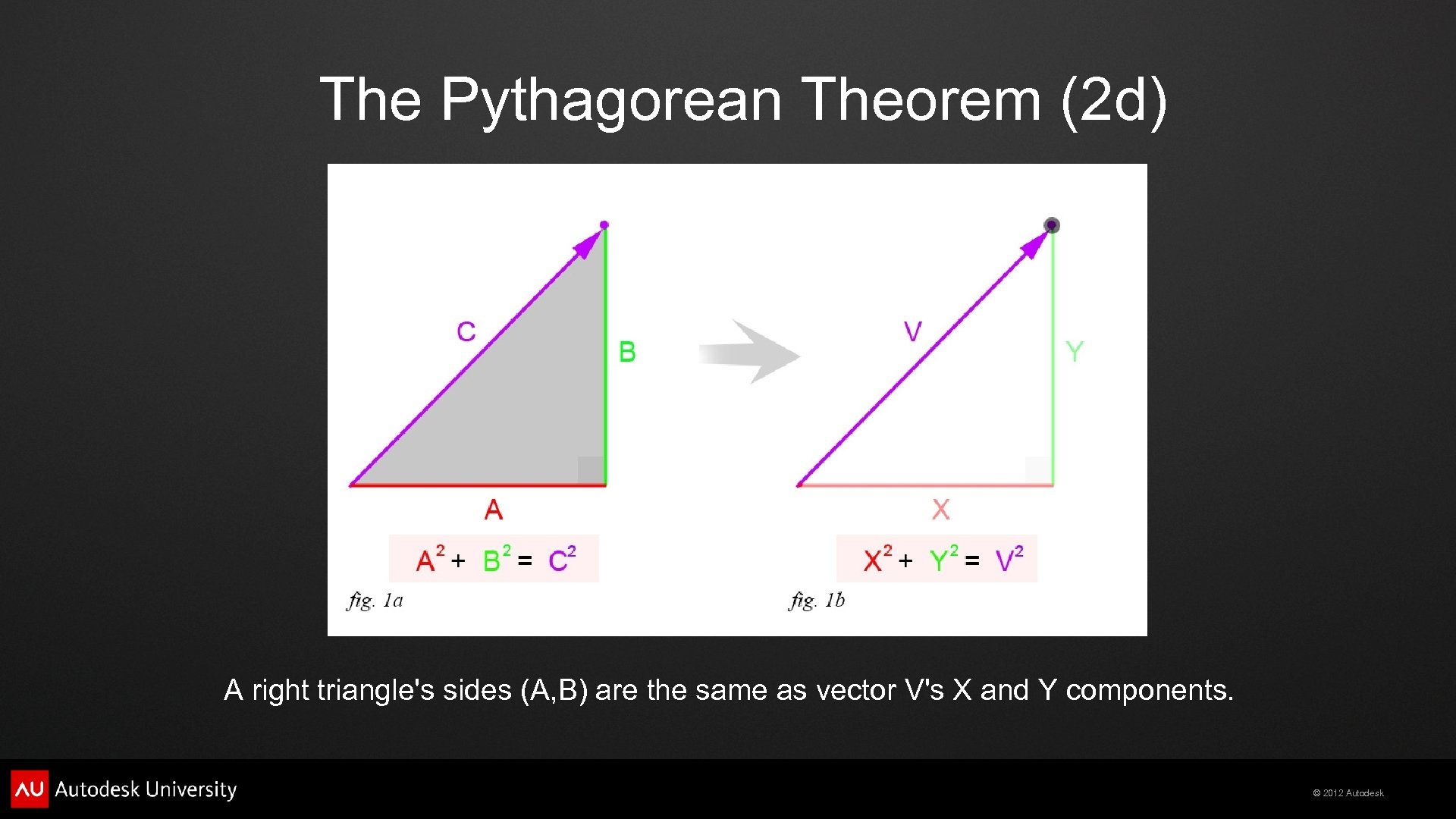
The Pythagorean Theorem (2 d) A right triangle's sides (A, B) are the same as vector V's X and Y components. © 2012 Autodesk
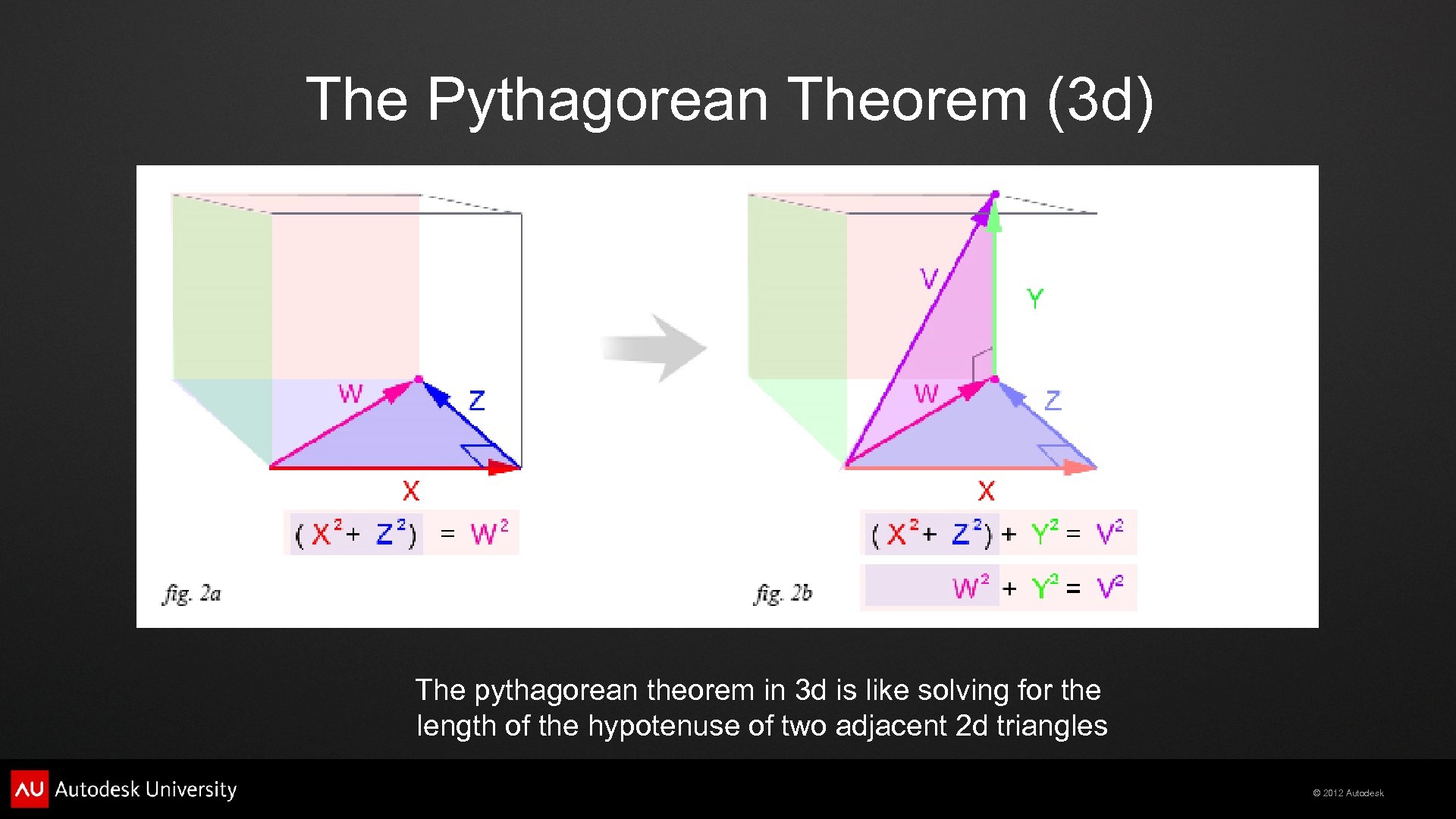
The Pythagorean Theorem (3 d) The pythagorean theorem in 3 d is like solving for the length of the hypotenuse of two adjacent 2 d triangles © 2012 Autodesk
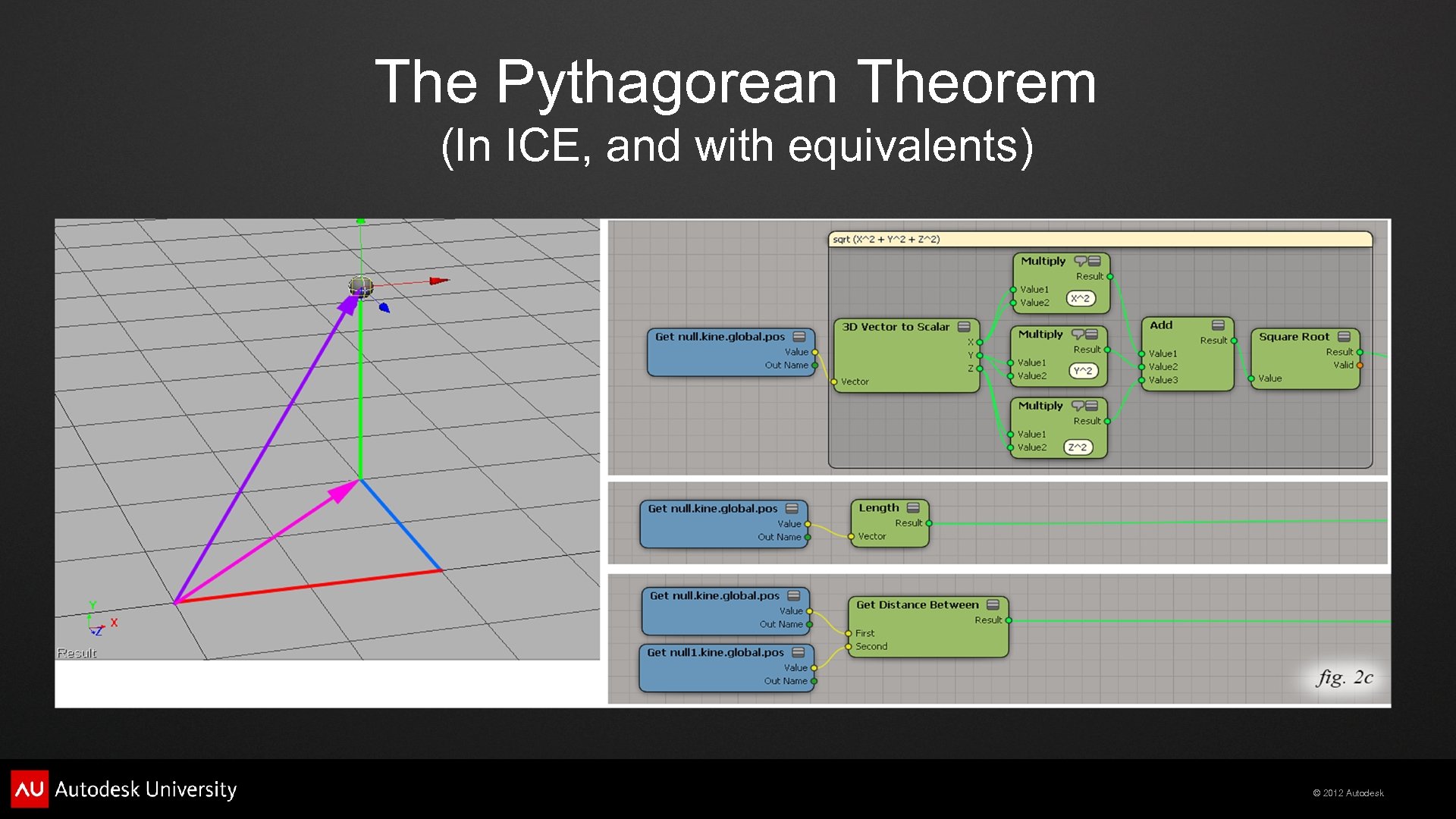
The Pythagorean Theorem (In ICE, and with equivalents) © 2012 Autodesk
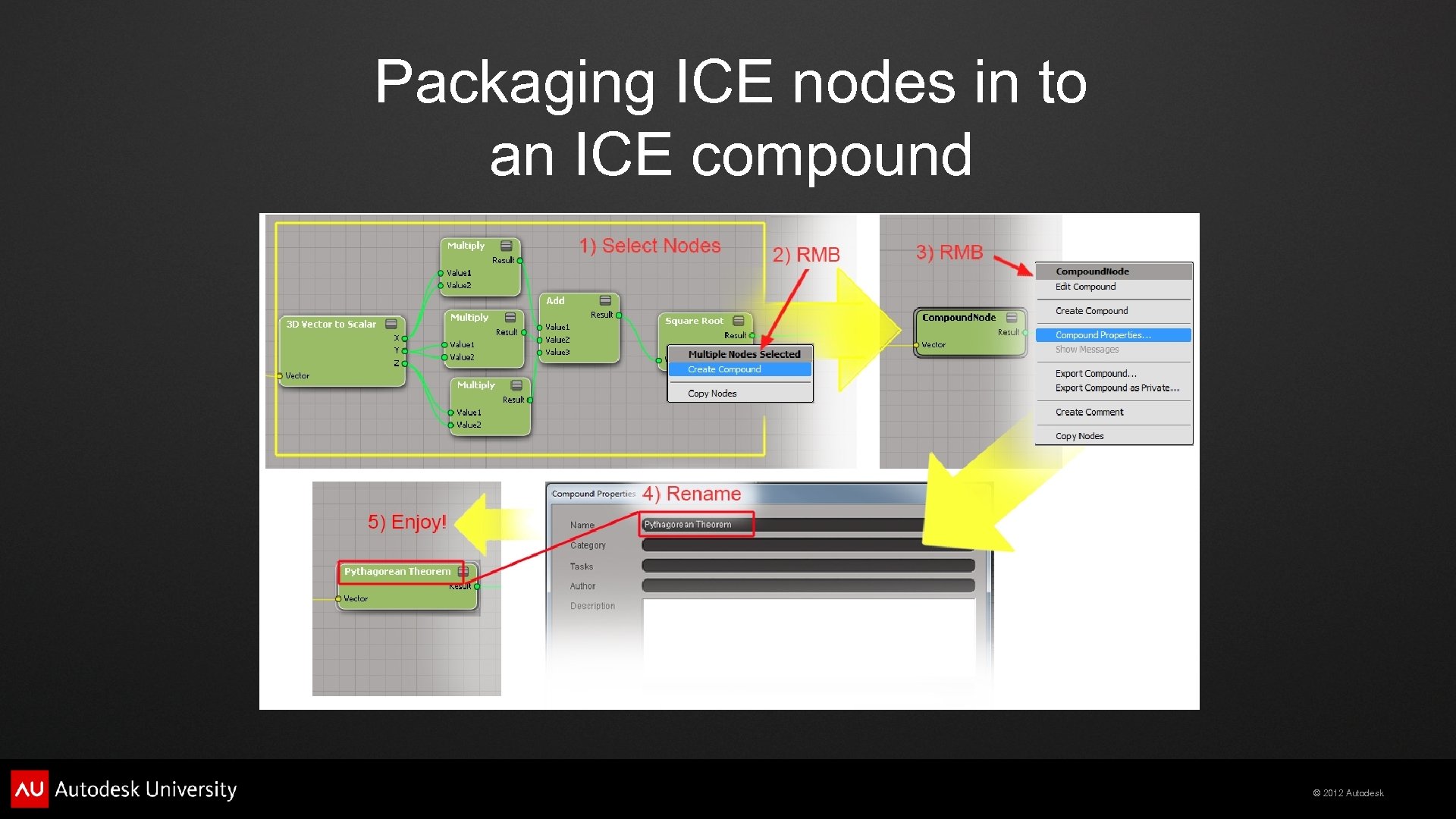
Packaging ICE nodes in to an ICE compound © 2012 Autodesk
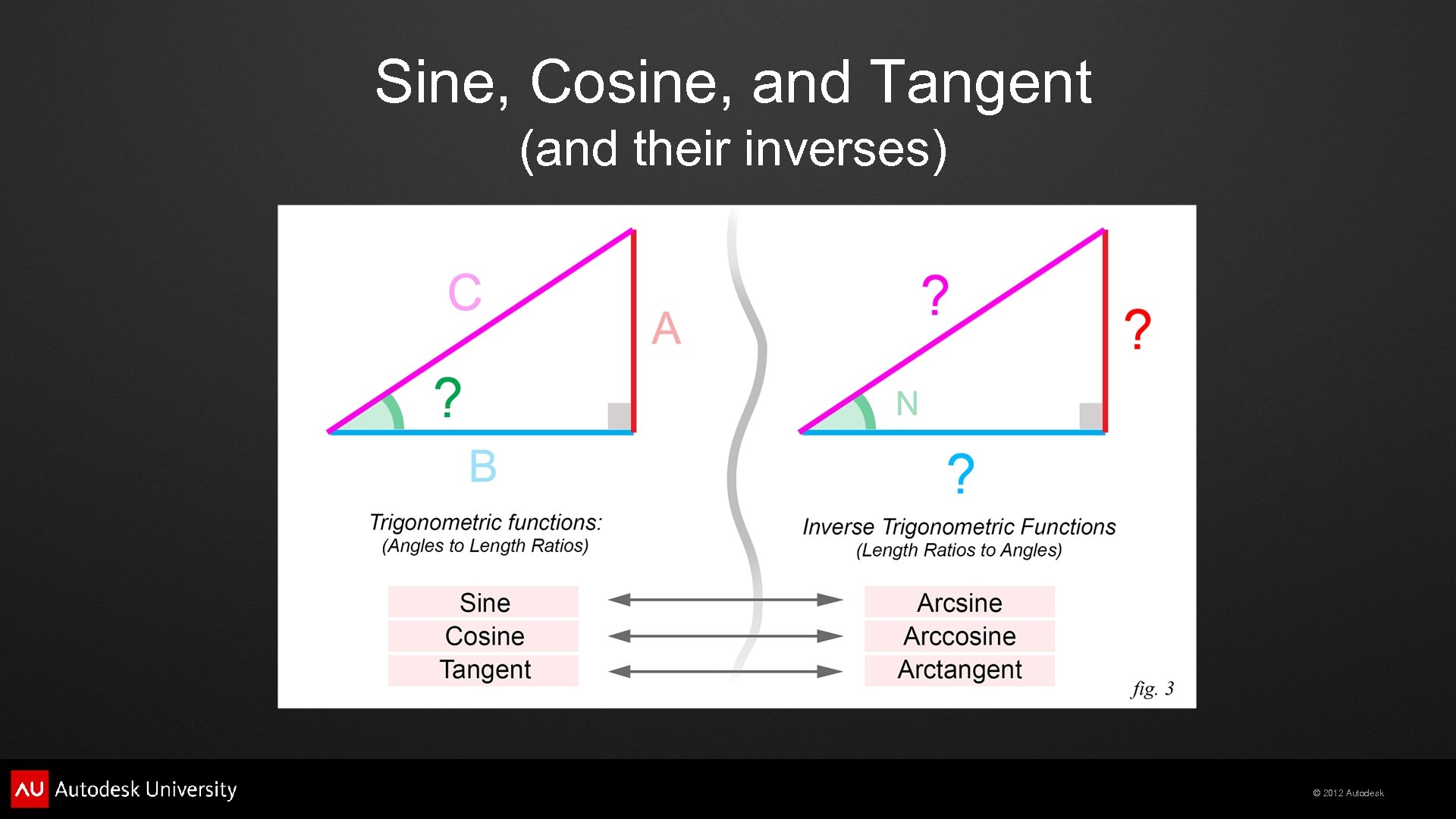
Sine, Cosine, and Tangent (and their inverses) © 2012 Autodesk
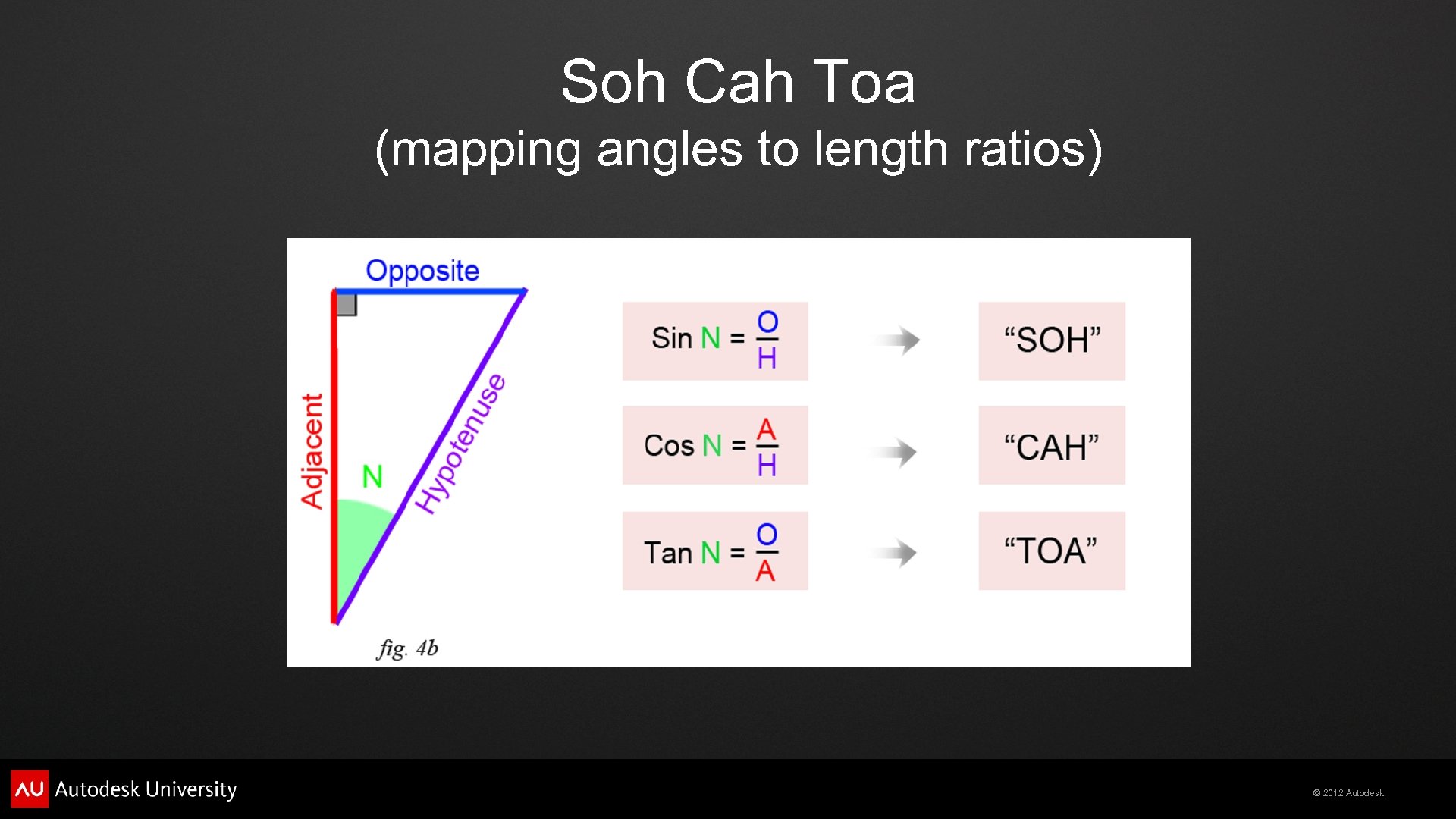
Soh Cah Toa (mapping angles to length ratios) © 2012 Autodesk

Inverse Trigonometric Functions (map length ratios to angles) © 2012 Autodesk
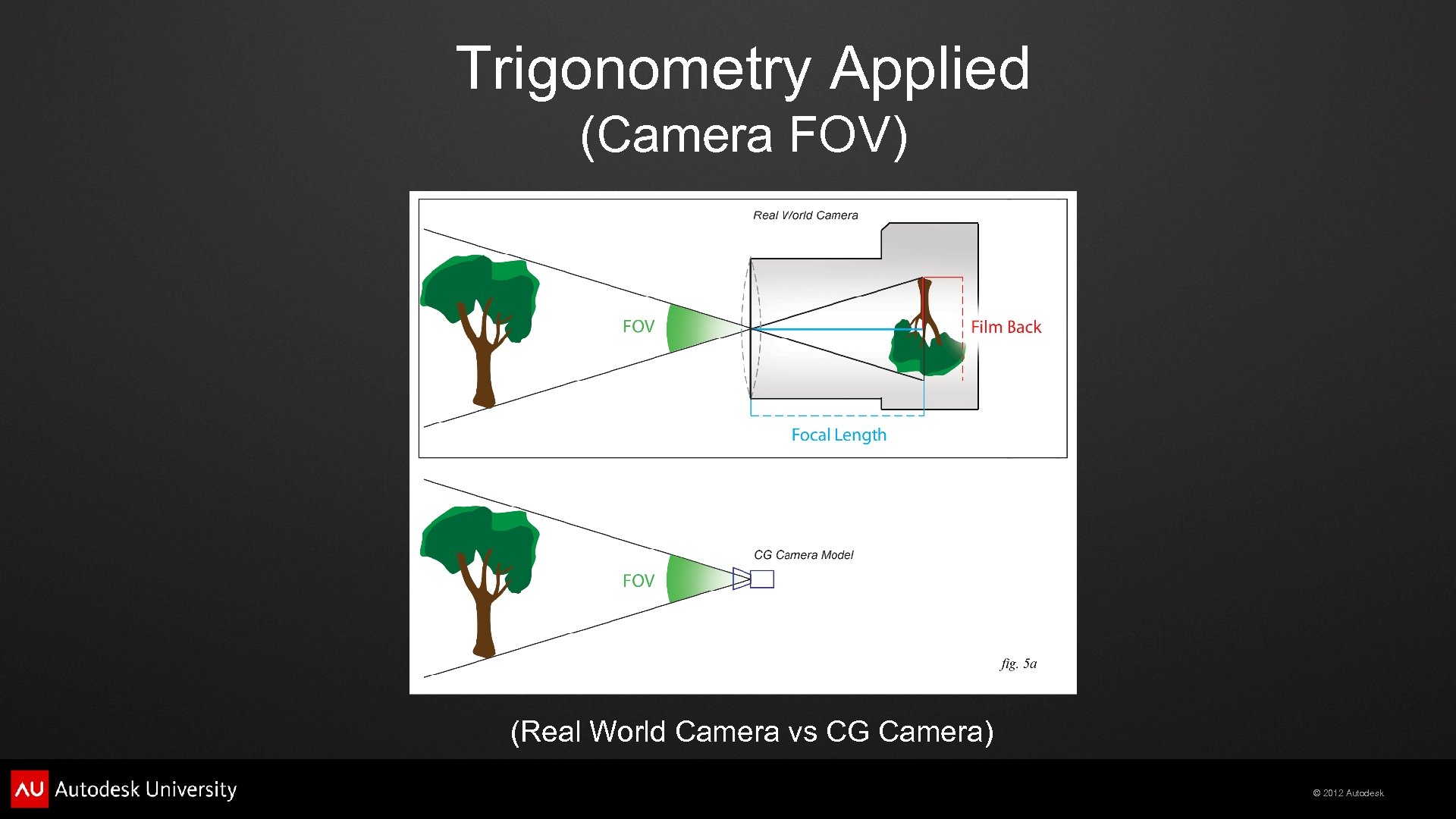
Trigonometry Applied (Camera FOV) (Real World Camera vs CG Camera) © 2012 Autodesk
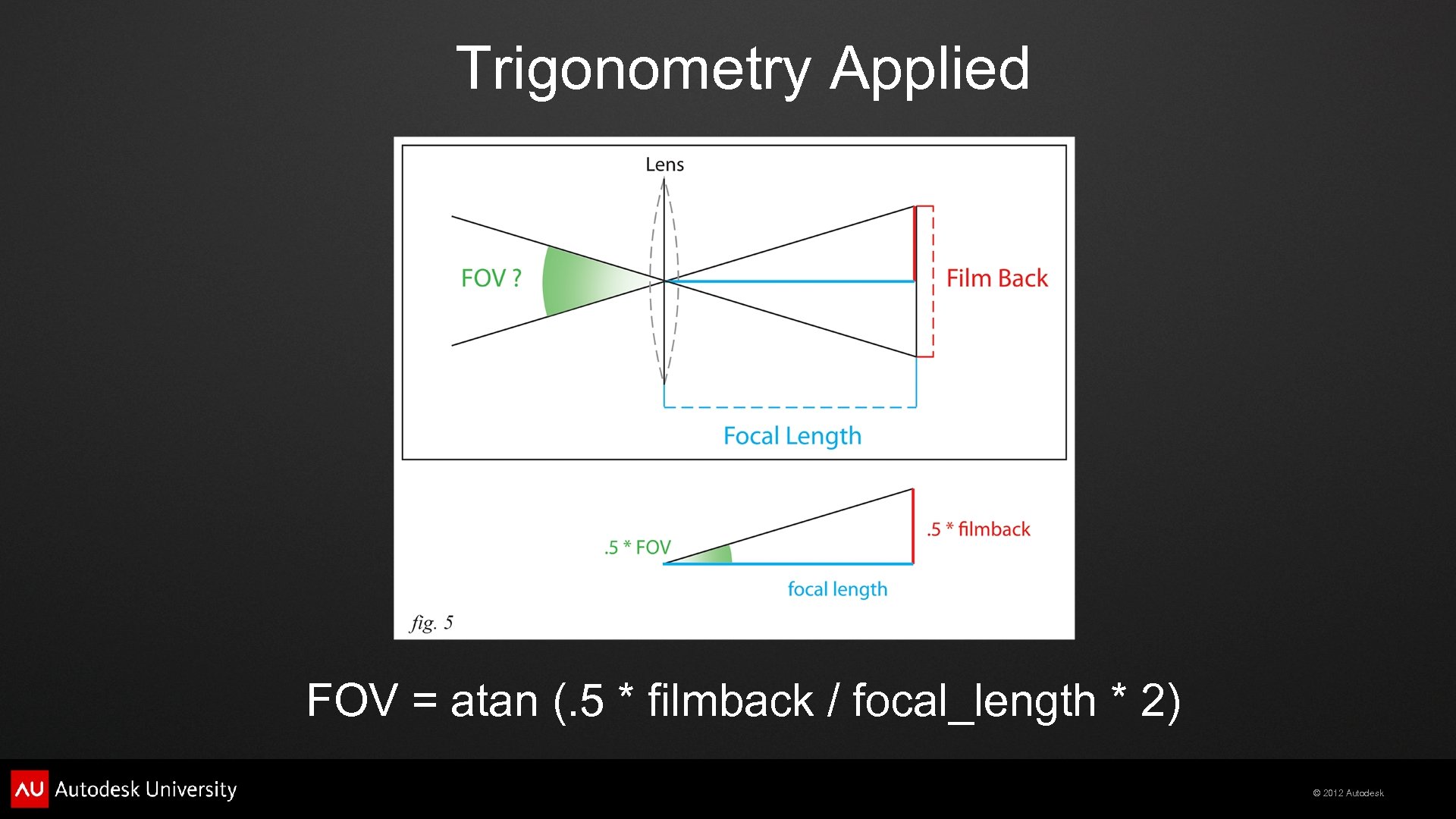
Trigonometry Applied FOV = atan (. 5 * filmback / focal_length * 2) © 2012 Autodesk
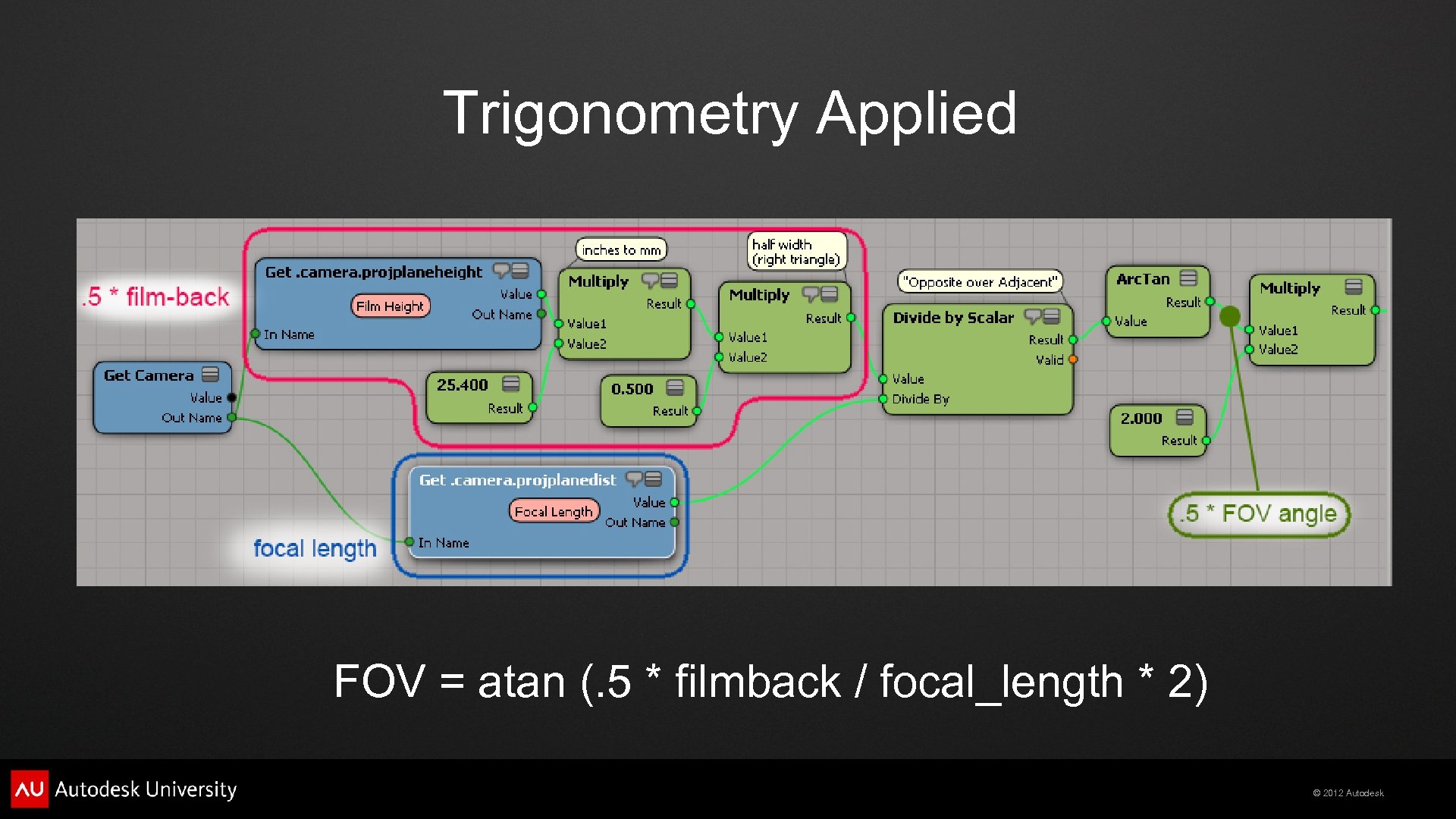
Trigonometry Applied FOV = atan (. 5 * filmback / focal_length * 2) © 2012 Autodesk
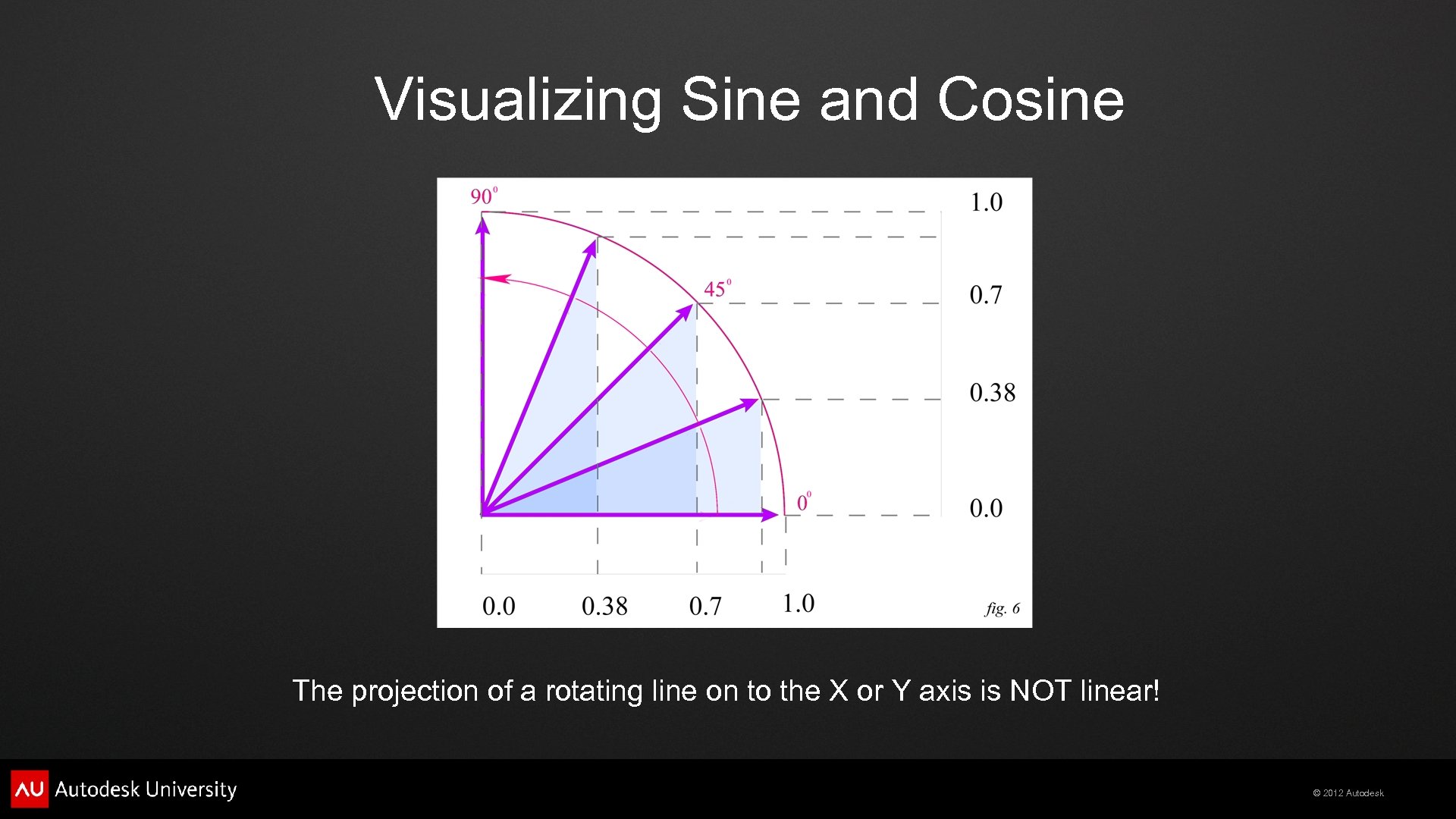
Visualizing Sine and Cosine The projection of a rotating line on to the X or Y axis is NOT linear! © 2012 Autodesk

Graphing Sine and Cosine Sine/Cosine are PERIODIC at intervals of 360 degrees, or 2 pi radians © 2012 Autodesk

Graphing Sine and Cosine follows X, Sine follows Y. Together, they create a Circle. © 2012 Autodesk
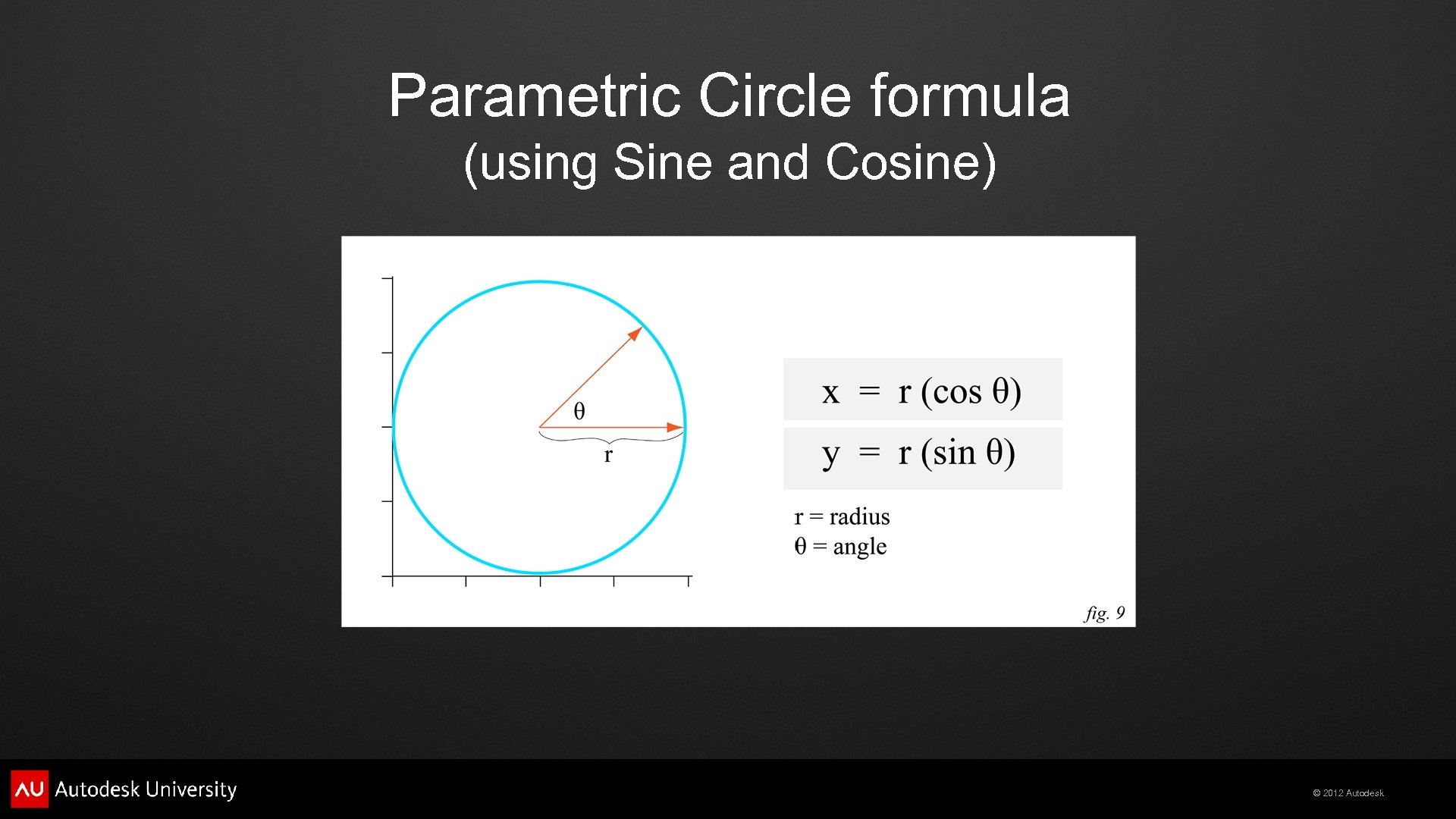
Parametric Circle formula (using Sine and Cosine) © 2012 Autodesk
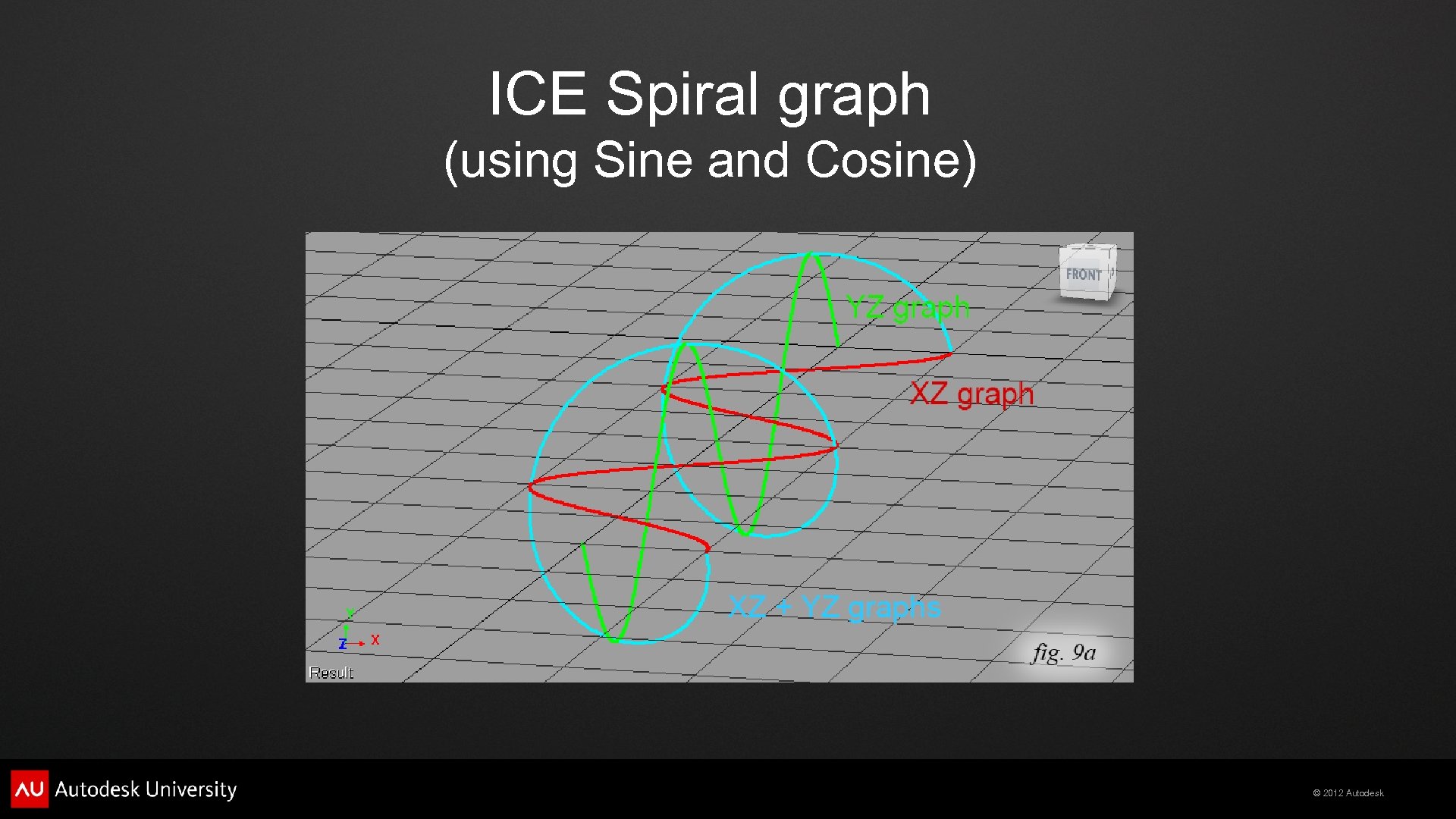
ICE Spiral graph (using Sine and Cosine) © 2012 Autodesk
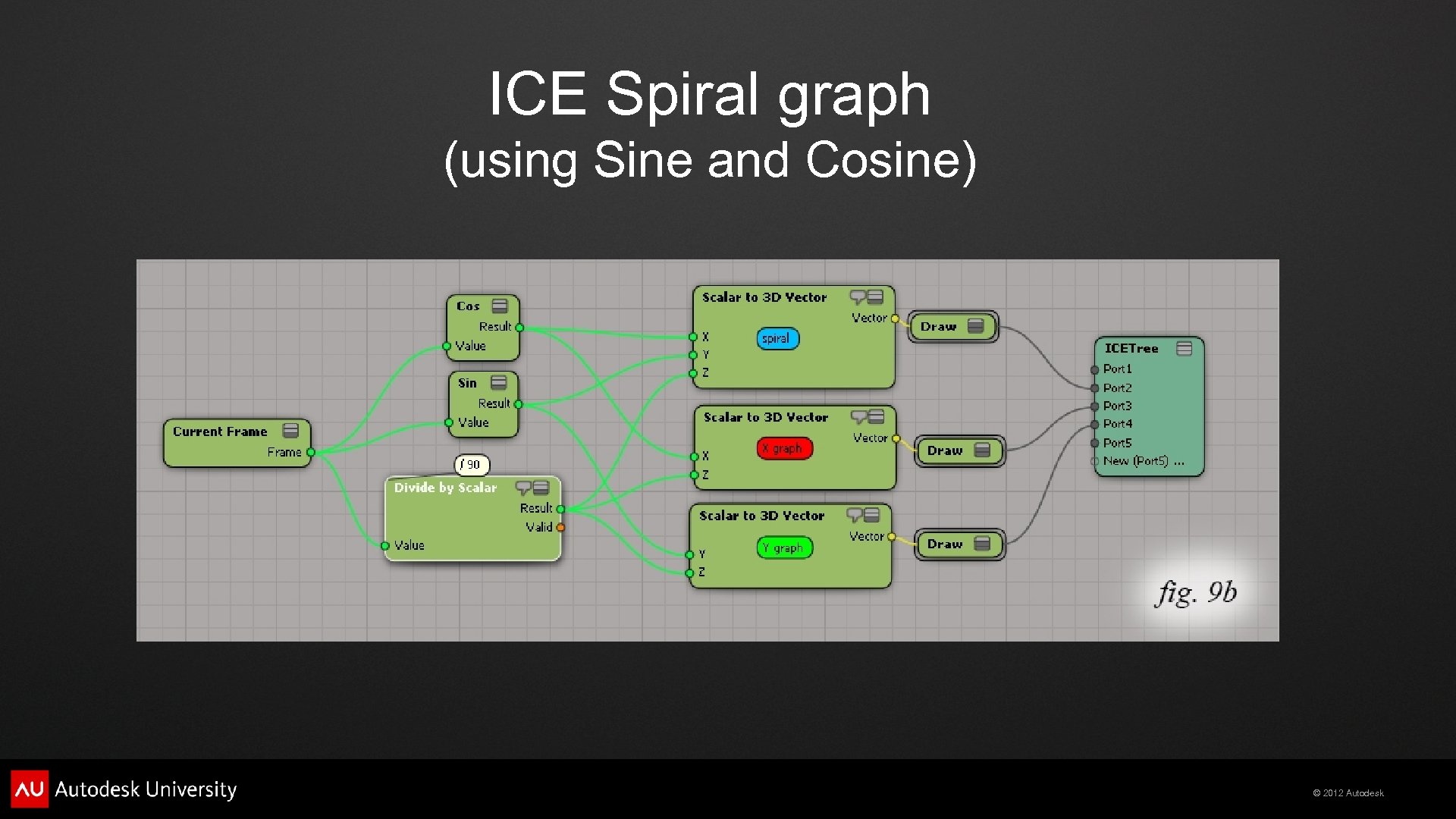
ICE Spiral graph (using Sine and Cosine) © 2012 Autodesk
ICE Spirals (hair and fibers) © 2012 Autodesk
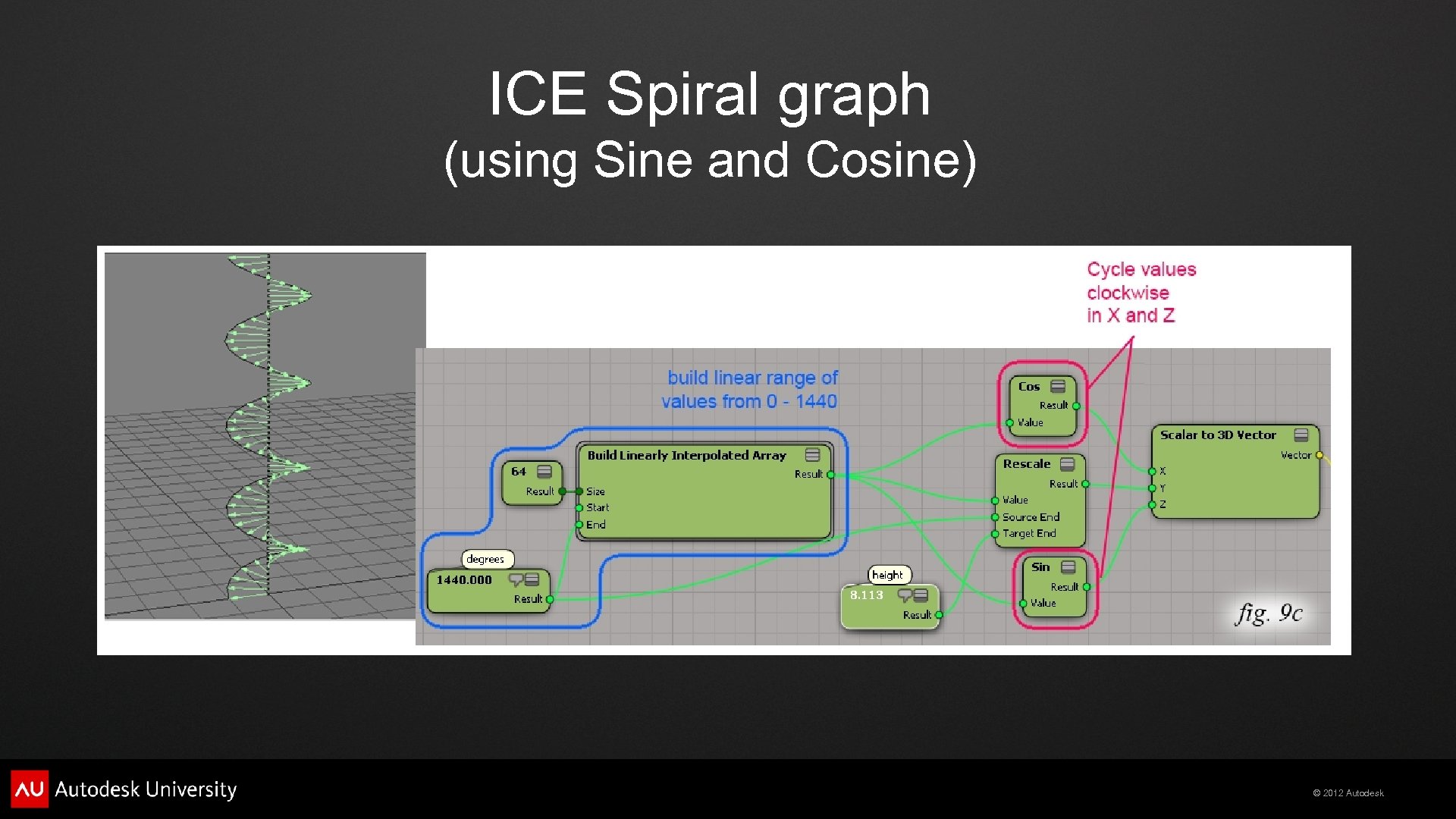
ICE Spiral graph (using Sine and Cosine) © 2012 Autodesk
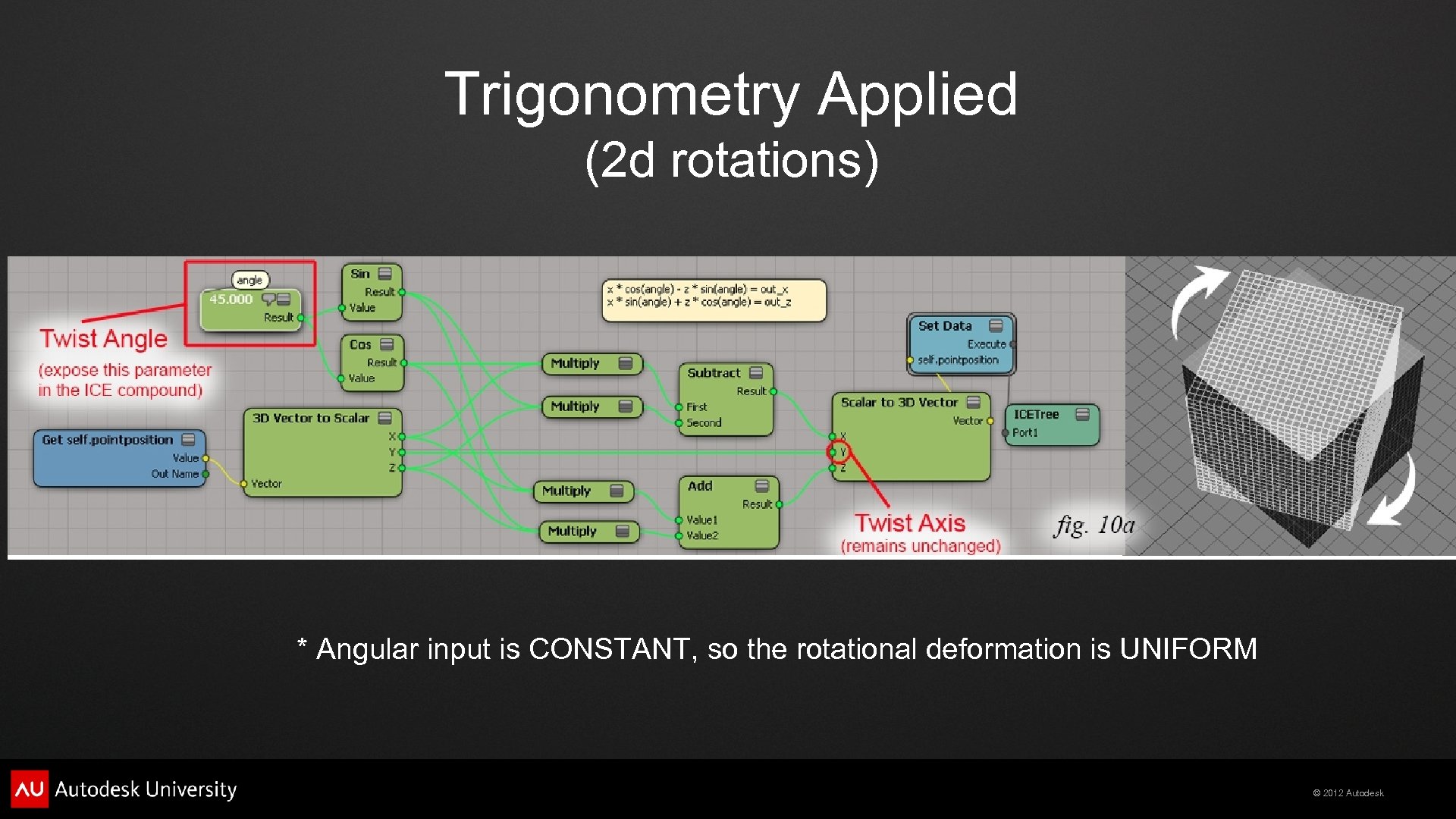
Trigonometry Applied (2 d rotations) * Angular input is CONSTANT, so the rotational deformation is UNIFORM © 2012 Autodesk
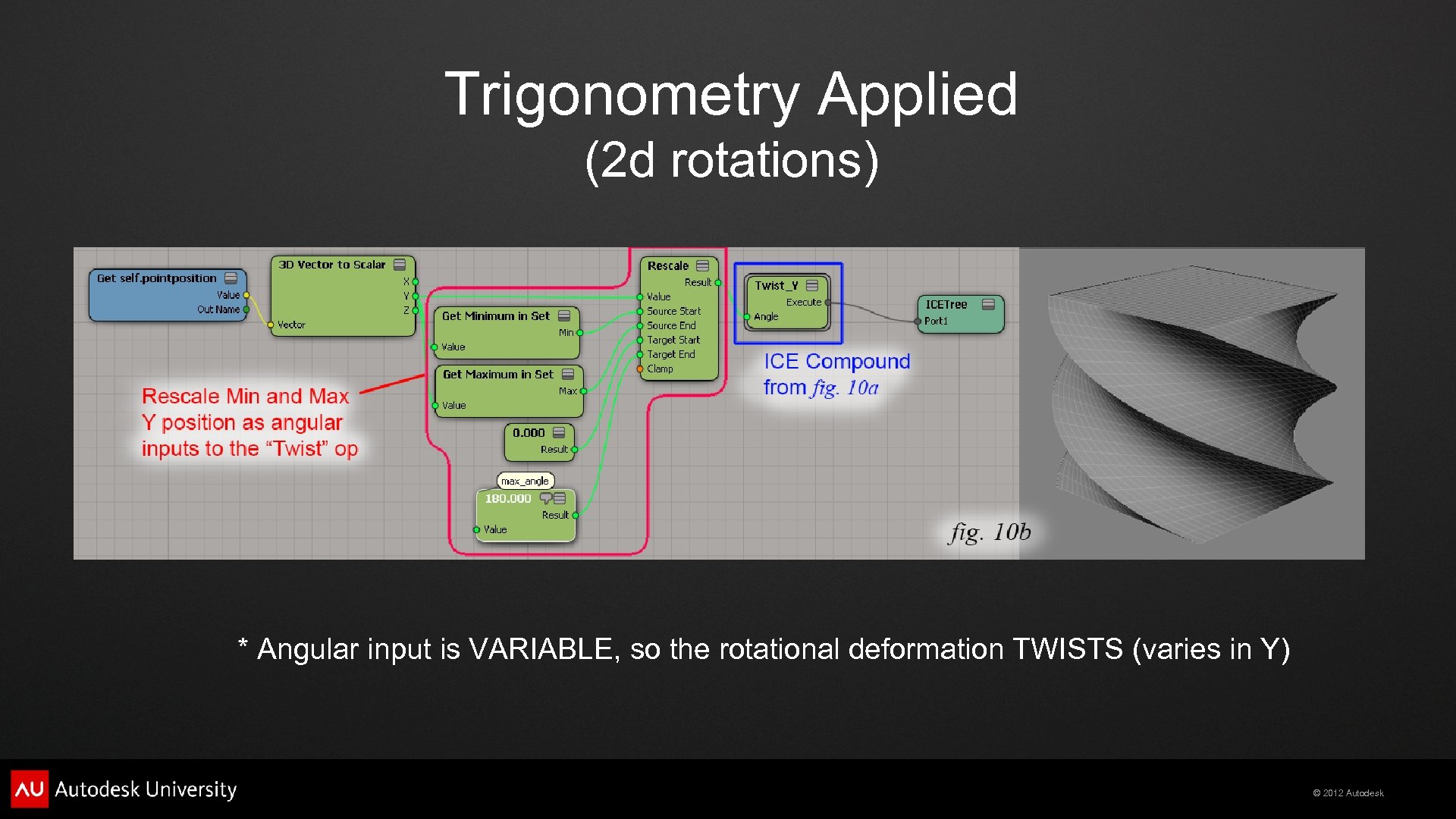
Trigonometry Applied (2 d rotations) * Angular input is VARIABLE, so the rotational deformation TWISTS (varies in Y) © 2012 Autodesk
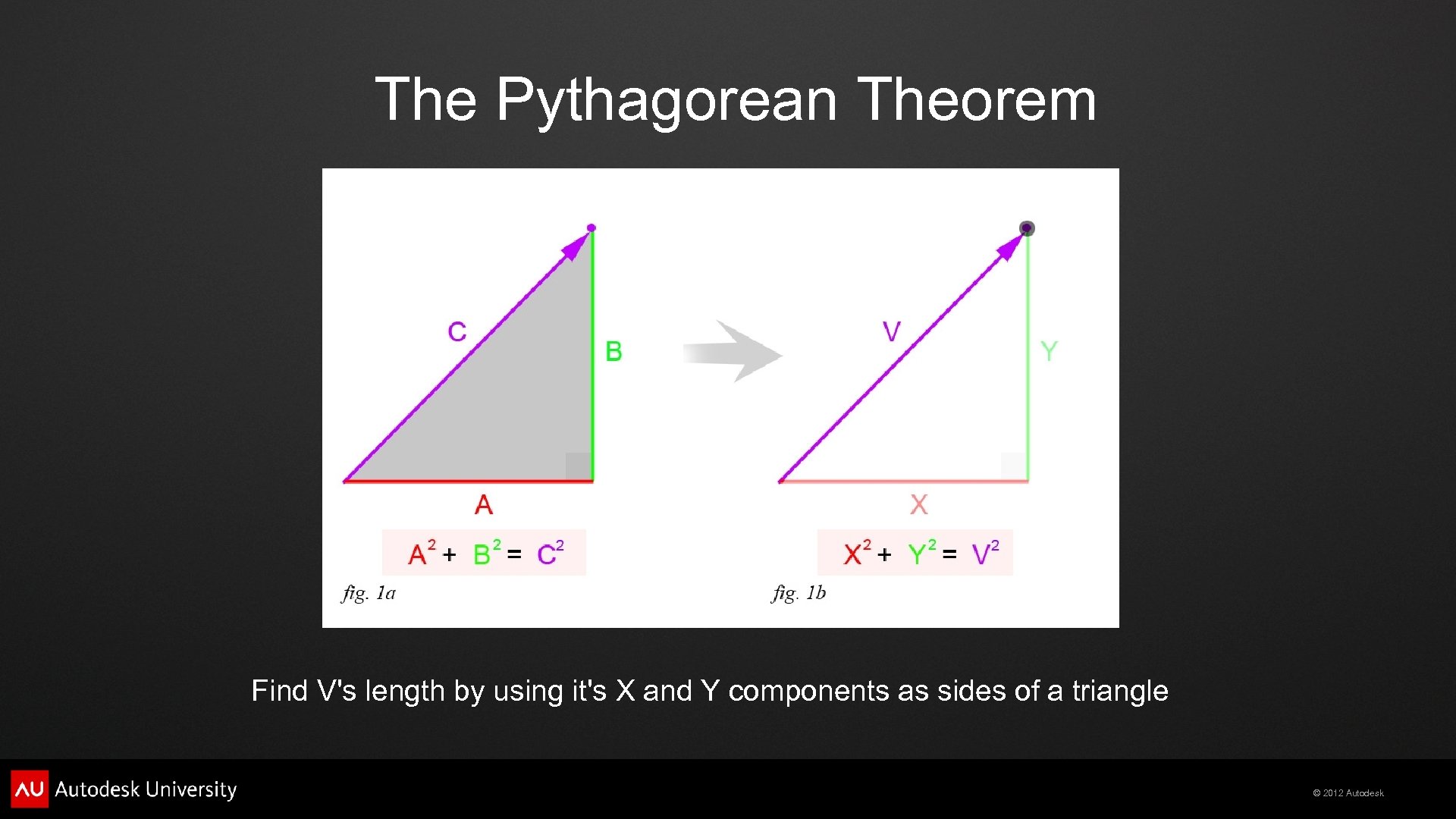
The Pythagorean Theorem Find V's length by using it's X and Y components as sides of a triangle © 2012 Autodesk
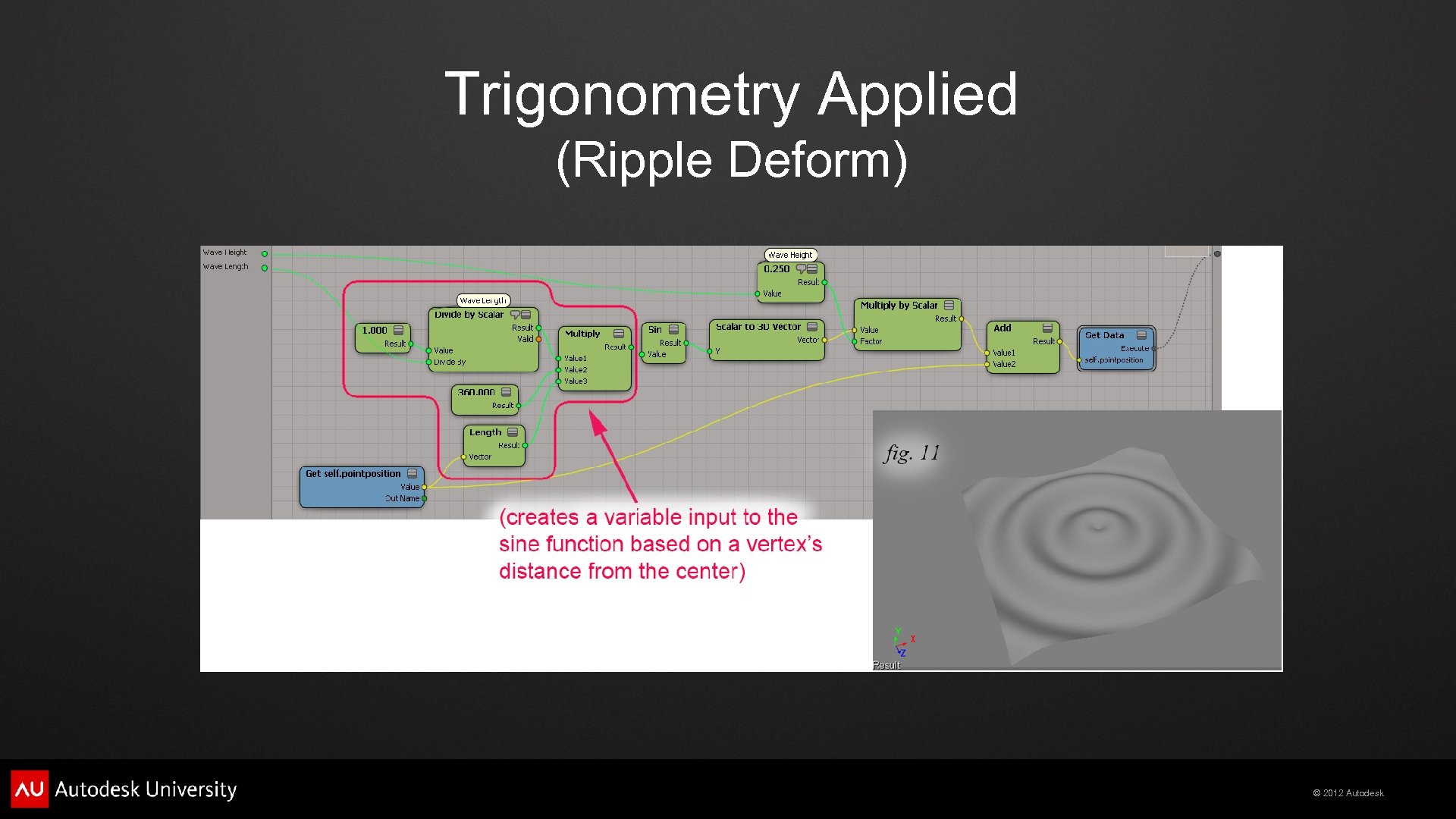
Trigonometry Applied (Ripple Deform) © 2012 Autodesk

Trigonometry Applied (Polar Coordinates) * note that we use Arc. Tan 2, not Arc. Tan © 2012 Autodesk
Vectors © 2012 Autodesk

A 2 d Vector is like an arrow or point in space (it's X, Y components form a triangle's sides) We can find V's length by using the pythagorean theorem © 2012 Autodesk

Vectors have two independent properties Direction, and Magnitude (length) We can find V's length by using the pythagorean theorem We can find V's direction by using trigonometry © 2012 Autodesk

Vector Addition (chaining them head to tail) Changing the order of operands does NOT affect the result © 2012 Autodesk

Vector Addition (as in adding forces) Changing the order of operands still does NOT affect the result © 2012 Autodesk

Vector Subtraction (same as adding the inverse) Changing the order of operands affects the result © 2012 Autodesk

Vector Subtraction (defining one point relative to another) (vectors that represent “Points in Space” versus vectors representing local “Direction Vectors”) © 2012 Autodesk

Vector Multiplication (3 kinds!) - Vector/Scalar (scaling a vector, produces a vector) - Vector/Vector (dot product, produces a scalar) - Vector/Vector (cross product, produces a vector) © 2012 Autodesk

Vector/Scalar Multiplication (scaling a vector) (multiply each of it's components by the scale factor) © 2012 Autodesk

Vector/Scalar Division (normalizing a vector) (dividing each of a vector's components by the vector's length produces a UNIT vector with length = 1. 0) © 2012 Autodesk

Vector Multiplication (dot product, or scalar product) Imagine it as an indicator of “parallel-ness”, (or as the projection of one vector on to another) © 2012 Autodesk

Vector Multiplication (dot product, or scalar product) We can perform backface detection and lambert Shading based on the sign (+ or -) of the dot product © 2012 Autodesk

Vector Multiplication (dot product, or scalar product) We can even use the dot product to do lambert shading in a compositor with pre-rendered normals © 2012 Autodesk

Vector Multiplication (dot product, or scalar product) It's the projection of vector A on to vector B © 2012 Autodesk

Vector Multiplication (dot product, or scalar product) The projection of vector A on to vector B forms a right triangle Relationship of sides to angle between A/B is trigonometric © 2012 Autodesk

Vector Multiplication (cross product, or vector product) Produces a third vector perpendicular to both of the two inputs © 2012 Autodesk

Vector Multiplication (cross product, or vector product) Like spokes on a wheel © 2012 Autodesk

Vector Multiplication (cross product, or vector product) The Cross Product is NOT commutative, switching operands inverts the result © 2012 Autodesk
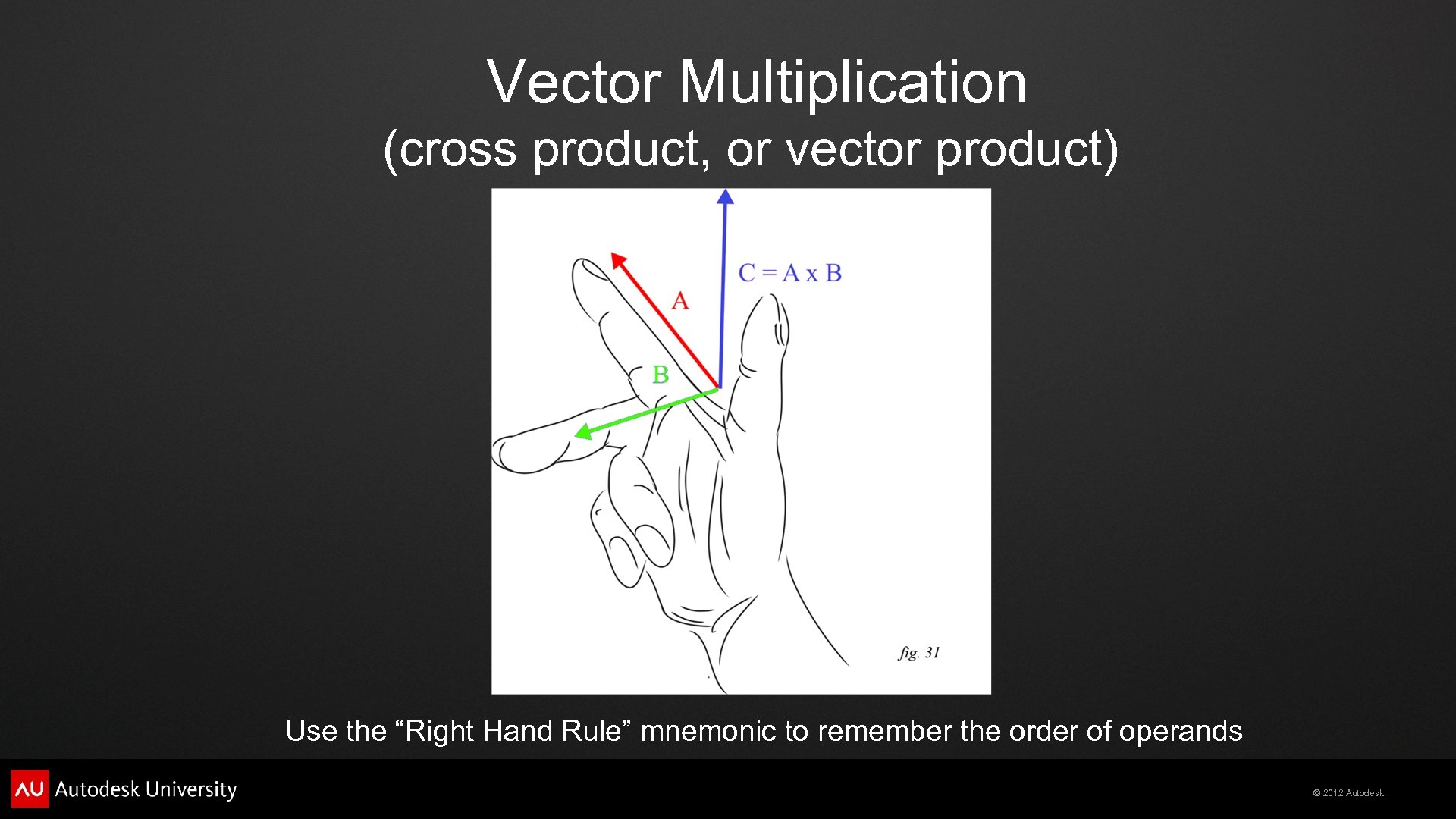
Vector Multiplication (cross product, or vector product) Use the “Right Hand Rule” mnemonic to remember the order of operands © 2012 Autodesk

Vector Multiplication (cross product, or vector product) Useful to produce orthogonal axes that define a coordinate space © 2012 Autodesk

Vector Multiplication (cross product, or vector product) Use vertex positions to define edges, then use the cross product to produce orthogonal axes that define a coordinate space © 2012 Autodesk
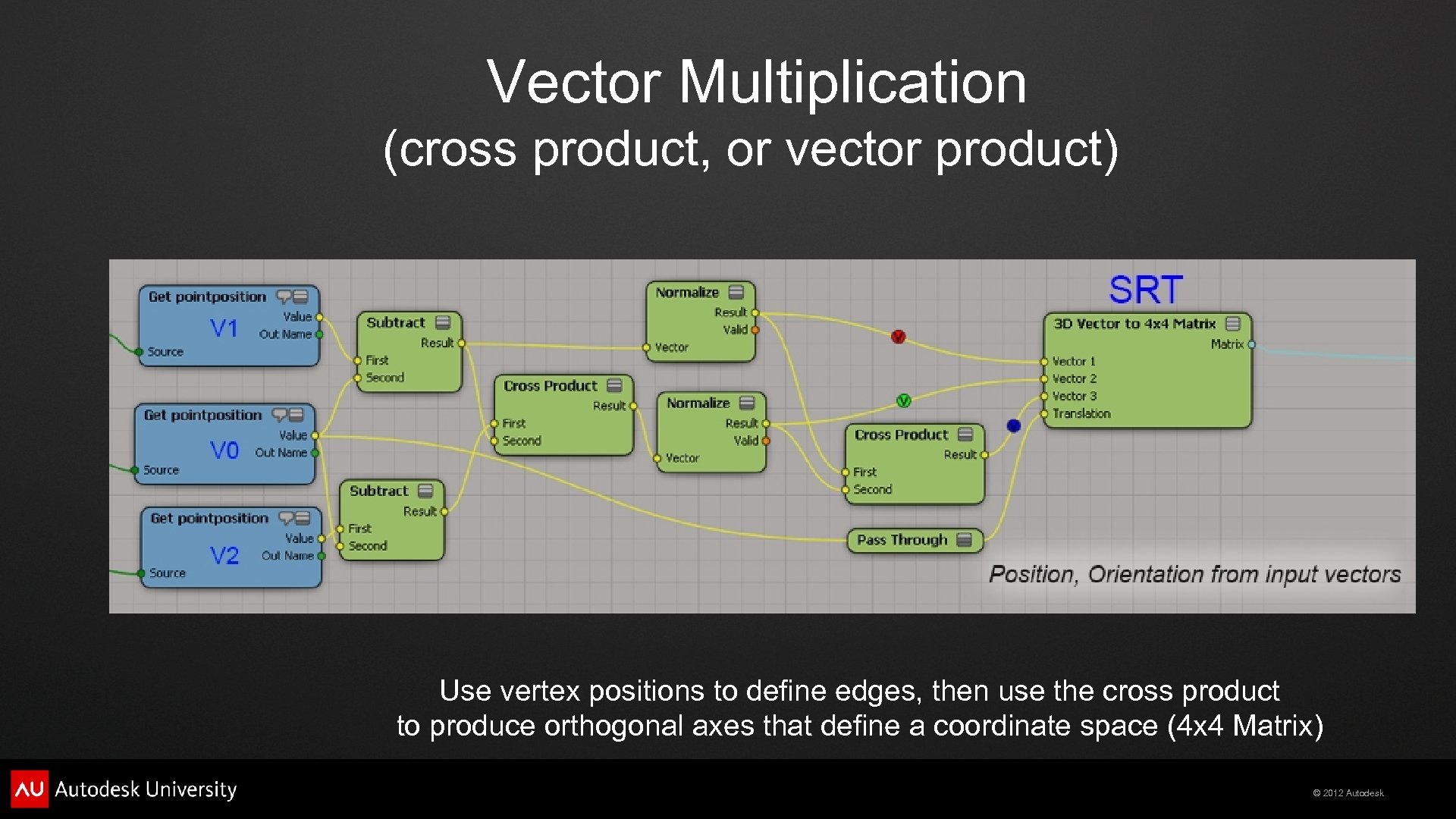
Vector Multiplication (cross product, or vector product) Use vertex positions to define edges, then use the cross product to produce orthogonal axes that define a coordinate space (4 x 4 Matrix) © 2012 Autodesk

Matrices/Transforms © 2012 Autodesk

4 x 4 Matrix (contains Scale, Rotate, and Translate) Can be displayed as Axes, Grid of Numbers, or SRT © 2012 Autodesk

4 x 4 Identity Matrix (zeroed Transforms) Each matrix ROW represents an axis vector © 2012 Autodesk

4 x 4 Matrix (scaled 2 x in Y) Each matrix ROW represents an axis vector the axis vector's LENGTH represents it's scaling on that axis © 2012 Autodesk
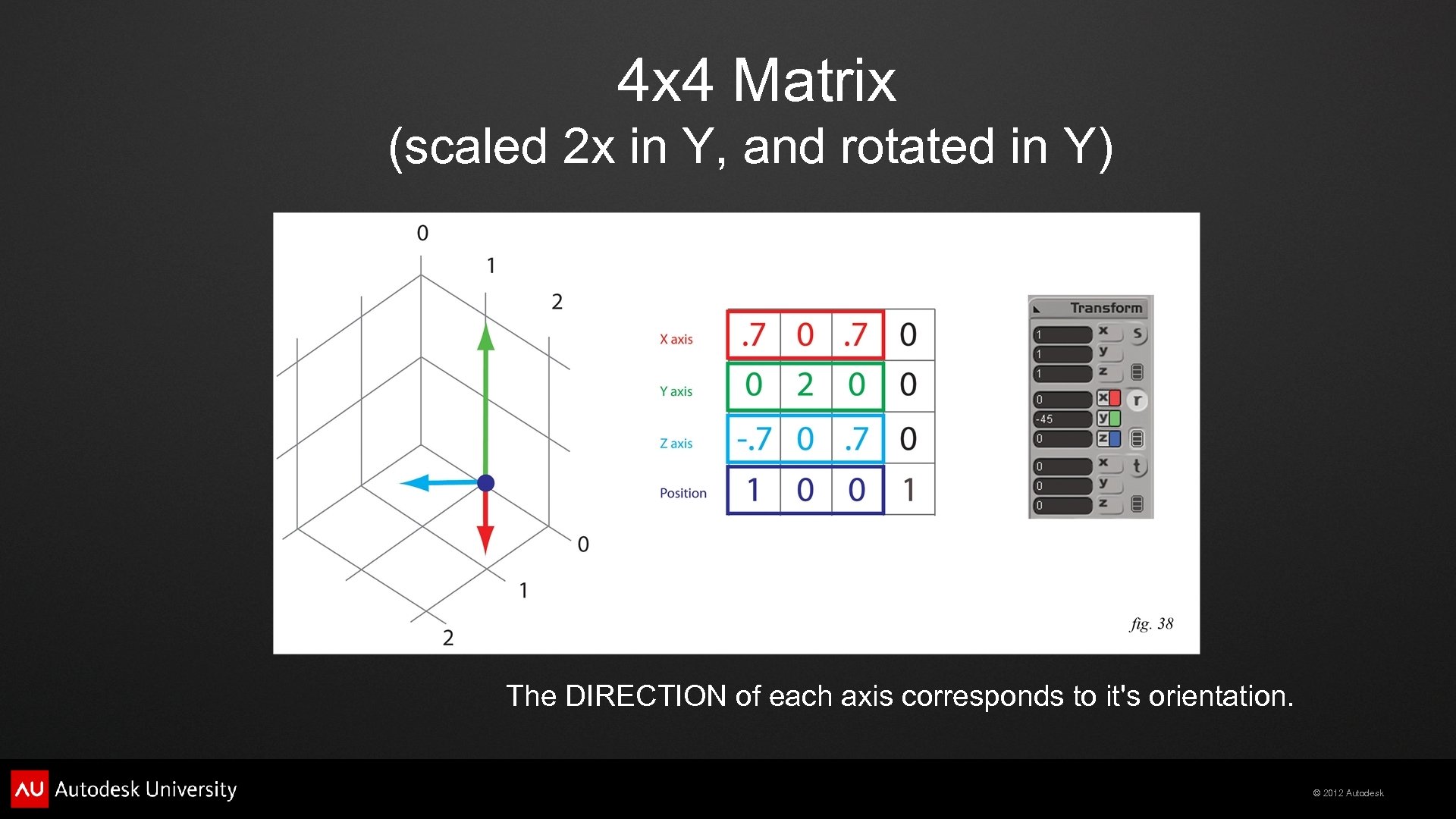
4 x 4 Matrix (scaled 2 x in Y, and rotated in Y) The DIRECTION of each axis corresponds to it's orientation. © 2012 Autodesk
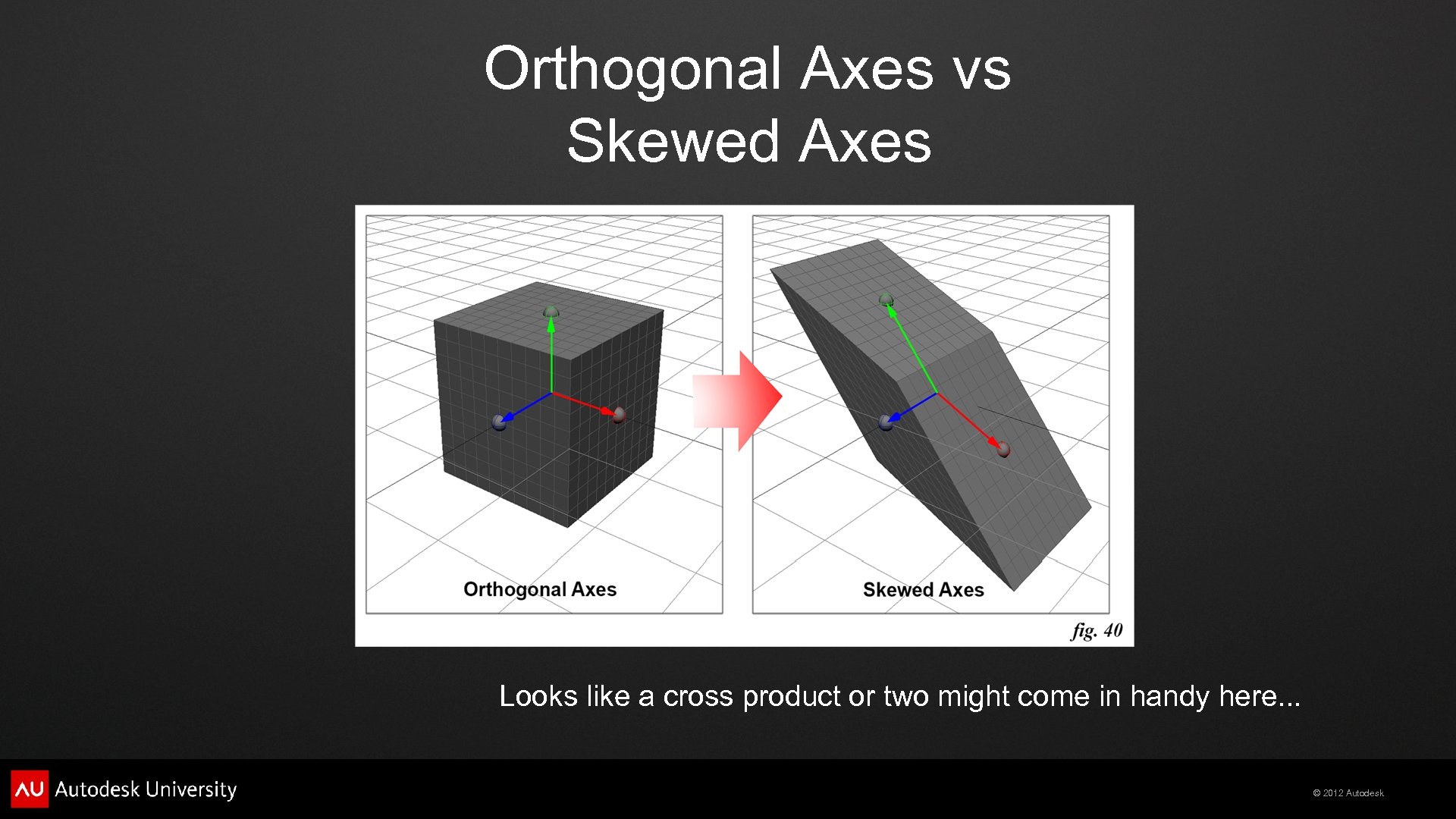
Orthogonal Axes vs Skewed Axes Looks like a cross product or two might come in handy here. . . © 2012 Autodesk
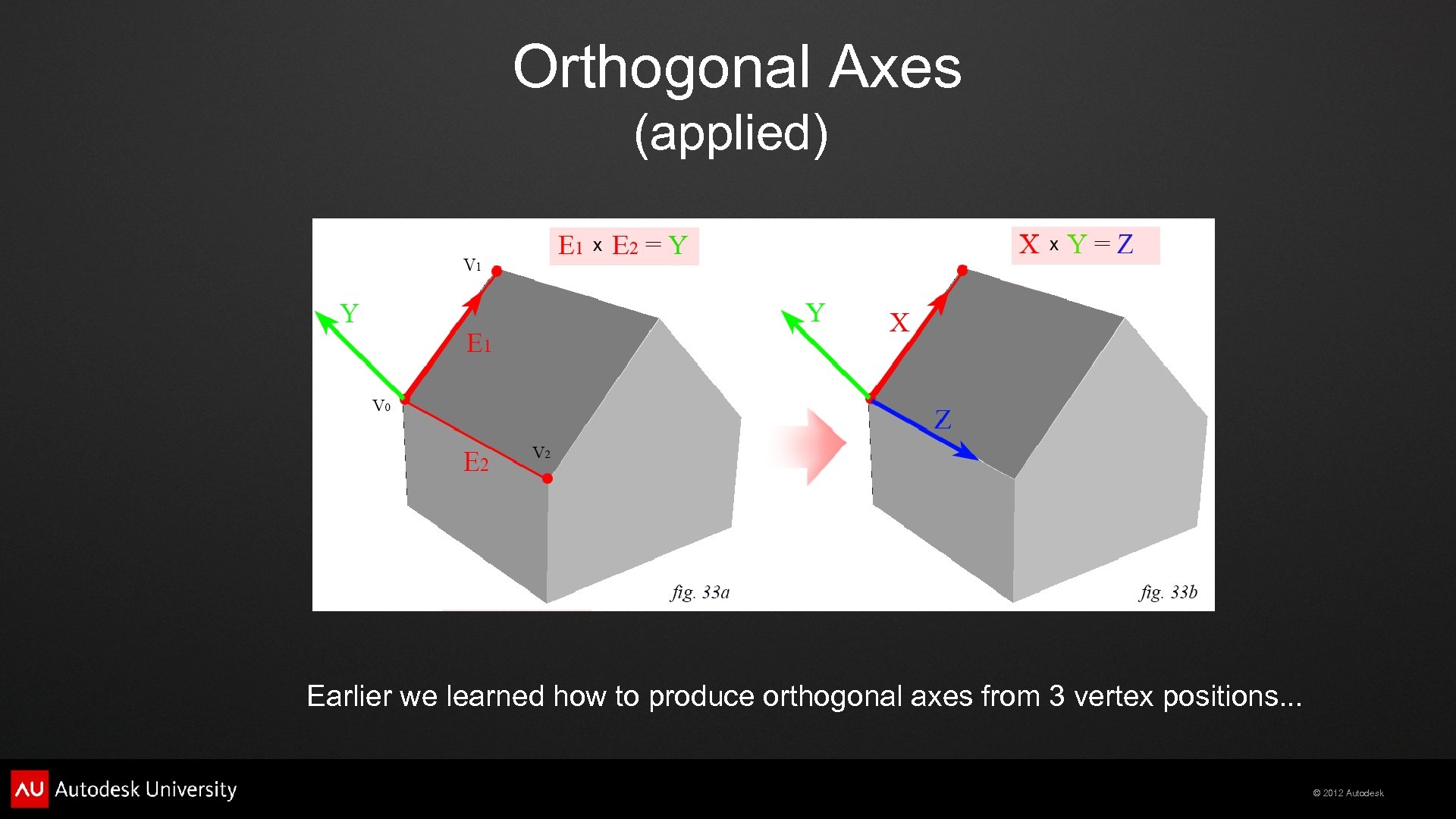
Orthogonal Axes (applied) Earlier we learned how to produce orthogonal axes from 3 vertex positions. . . © 2012 Autodesk
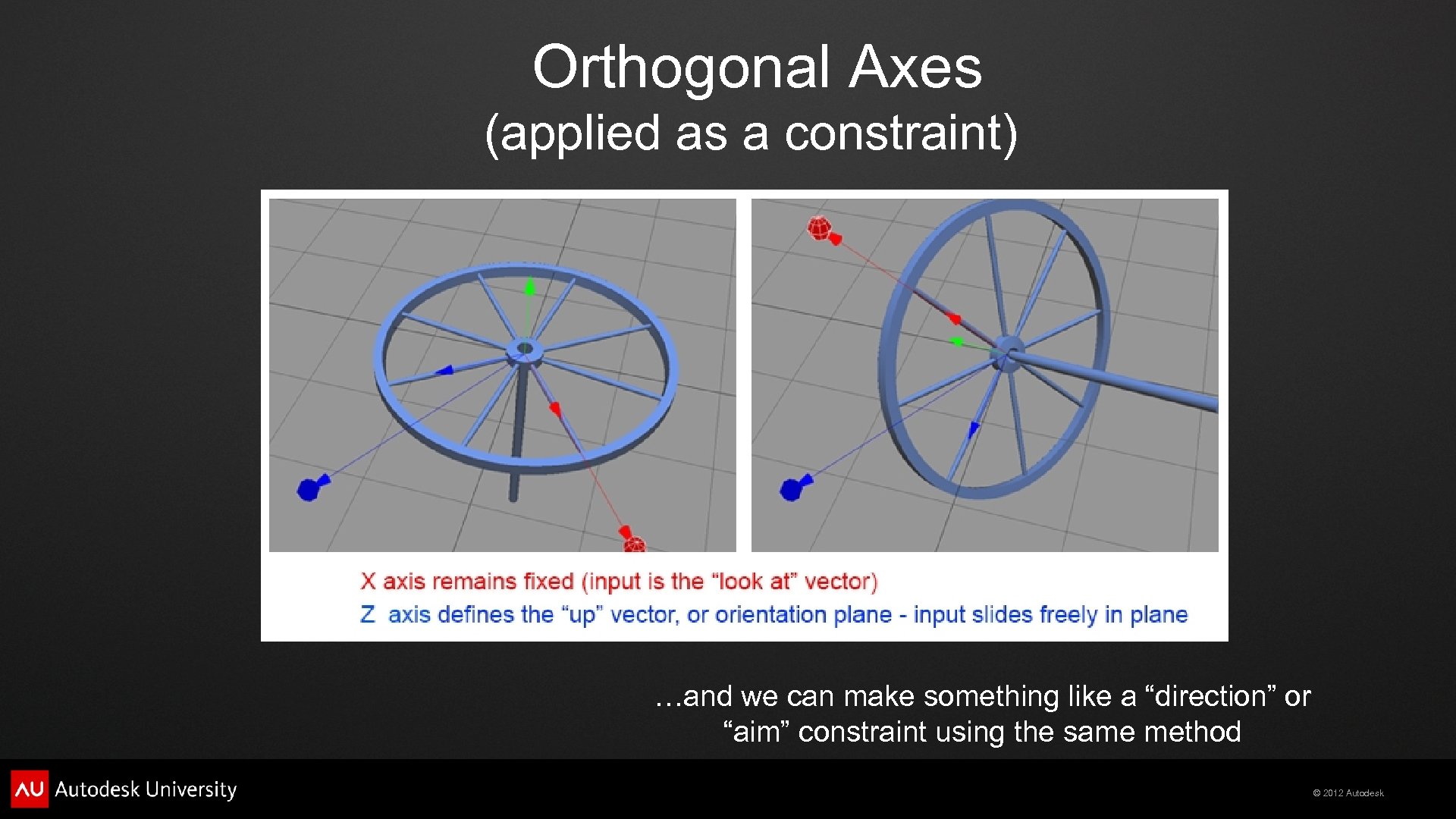
Orthogonal Axes (applied as a constraint) …and we can make something like a “direction” or “aim” constraint using the same method © 2012 Autodesk

Matrix Multiplication We can use Matrix Multiplication to perform the equivalent of PARENTING operations, to place the elephant on the roof of the house © 2012 Autodesk

Matrix Multiplication We will examine TWO types of Matrix multiplication. - Vector/Matrix Multiplication (transforming vectors) - Matrix/Matrix Multiplcation (“parenting” operations) © 2012 Autodesk

Vector/Matrix Multiplication deforms the elephant's points on the roof. (similar to a “skinning” or “envelope” deformation) © 2012 Autodesk

Vector/Matrix Multiplication deforms the elephant's points on the roof. (similar to a “skinning” or “envelope” deformation) © 2012 Autodesk

Matrix/Matrix Multiplication transforms the elephant's SRT on to the roof. (similar to a “parenting” operation) © 2012 Autodesk

Matrix/Matrix Multiplication transforms the elephant's SRT on to the roof. (similar to a “parenting” operation) © 2012 Autodesk

Questions? © 2012 Autodesk

Autodesk, Auto. CAD* [*if/when mentioned in the pertinent material, followed by an alphabetical list of all other trademarks mentioned in the material] are registered trademarks or trademarks of Autodesk, Inc. , and/or its subsidiaries and/or affiliates in the USA and/or other countries. All other brand names, product names, or trademarks belong to their respective holders. Autodesk reserves the right to alter product and services offerings, and specifications and pricing at any time without notice, and is not responsible for typographical or graphical errors that may appear in this document. © 2012 Autodesk, Inc. All rights reserved. © 2012 Autodesk
6e11e3e609d96fc0e5f7f9ac7eb2a8e6.ppt