Содержание предыдущей лекции Уравнение Шредингера Волновая функция и

Содержание предыдущей лекции Уравнение Шредингера Волновая функция и ее статистический смысл. Временное уравнение Шредингера. Уравнение Шредингера для стационарных состояний. 1

Контрольный вопрос Частица совершает простые гармонические колебания в состоянии n = 0. Наиболее вероятным значением положения частицы согласно квантовой механике являются (a) x =0 (б) x = A (в) все значения x равновероятны. С классической точки зрения наиболее вероятными являются положения x = A, поскольку вблизи них частица движется с наименьшей скоростью. Квантовая механика, как следует из графика, предсказывает максимальную плотность вероятности в основном состоянии при x = 0. (a) 2

Содержание сегодняшней лекции Строение атома Модель атома водорода Резерфорда и ее недостатки. Закономерности в спектре излучения атома водорода. Постулаты Бора. Квантовые числа и их физический смысл. Энергетические уровни. Спектр излучения. Спин электрона. Принцип Паули. Распределение электронов в атоме по состояниям. 3

Модель атома Резерфорда и ее недостатки Времена Ньютона: атом – маленькая неделимая сфера. Дж. Томсон, 1898 г. модель атома «сливовый пудинг» электроны распределены внутри положительного заряда ядра (изюминки в высоком пудинге). Эрнст Резерфорд и его студенты Ганс Гейгер и Эрнест Марсден (1911 г. ) исследования, показавшие, что модель Томсона неверна. 4

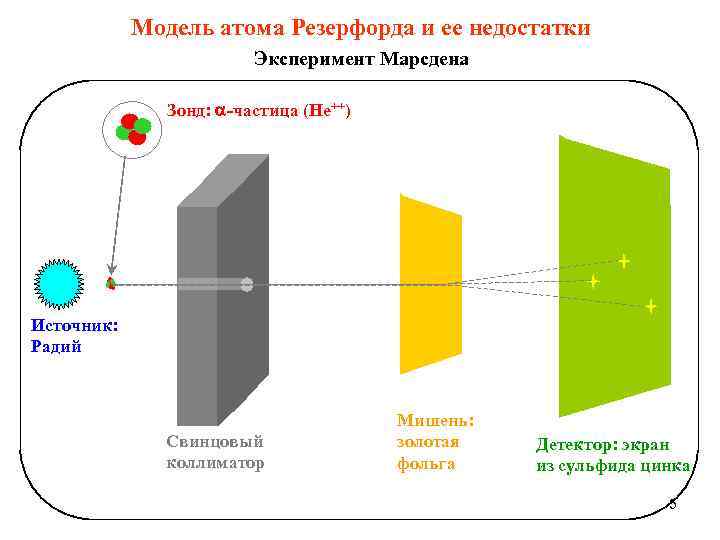Модель атома Резерфорда и ее недостатки Эксперимент Марсдена Зонд: -частица (He++) Источник: Радий Свинцовый коллиматор Мишень: золотая фольга Детектор: экран из сульфида цинка 5

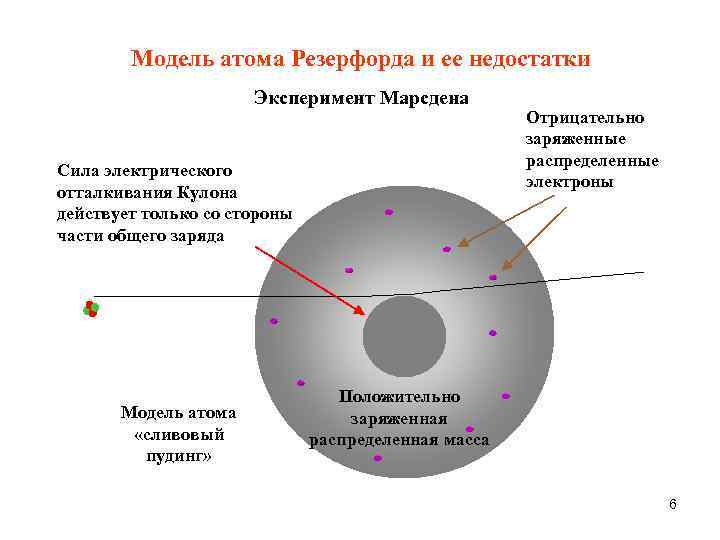Модель атома Резерфорда и ее недостатки Эксперимент Марсдена Сила электрического отталкивания Кулона действует только со стороны части общего заряда Модель атома «сливовый пудинг» Отрицательно заряженные распределенные электроны Положительно заряженная распределенная масса 6

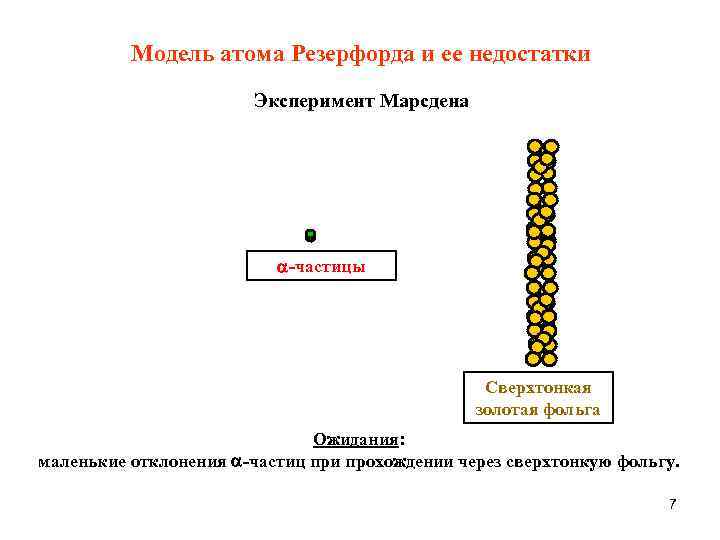Модель атома Резерфорда и ее недостатки Эксперимент Марсдена -частицы Сверхтонкая золотая фольга Ожидания: маленькие отклонения -частиц при прохождении через сверхтонкую фольгу. 7

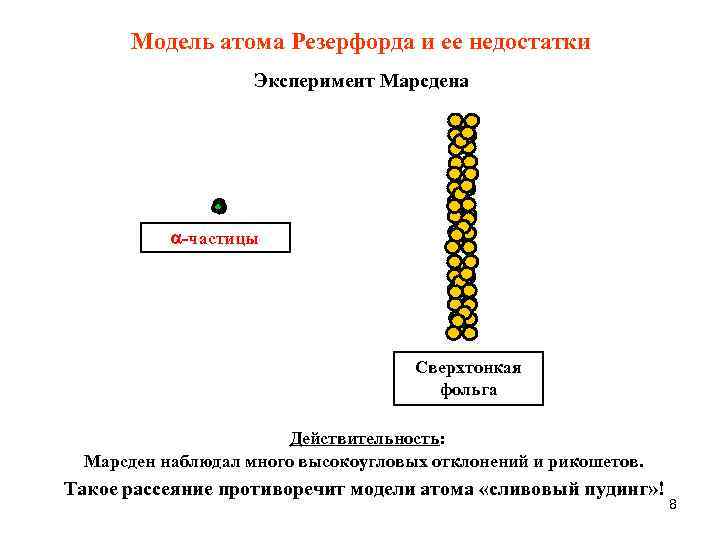Модель атома Резерфорда и ее недостатки Эксперимент Марсдена -частицы Сверхтонкая фольга Действительность: Марсден наблюдал много высокоугловых отклонений и рикошетов. Такое рассеяние противоречит модели атома «сливовый пудинг» ! 8

Модель атома Резерфорда и ее недостатки Выводы Резерфорда: заряженная масса не распределена по всему объему атома; наблюдаемые отклонения -частиц могут происходить, если заряд сконцентрирован в центре объема, соответствующего 0, 0001 атомного диаметра; смерть модели атома «сливовый пудинг» и рождение ядерной модели. 9

Модель атома Резерфорда и ее недостатки Положительный заряд сконцентрирован в ядре атома, размеры которого малы по сравнению с размерами атома. Все электроны, принадлежащие атому, движутся по орбитам в пределах относительно большого объема за пределами ядра и вокруг него. 10

Модель атома Резерфорда и ее недостатки Два основных фундаментальных затруднения планетарной модели Резерфорда: 1) Не может объяснить почему атомы испускают (и поглощают) э-м излучение с определенными характерными частотами и никакое другое. 2) Электроны, находящиеся под воздействием центростремительного ускорения, должны излучать э-м волны и терять энергию за счет излучения – электроны должны быть захвачены ядром и атом должен разрушиться. 11

Закономерности в спектре излучения атома водорода шведский спектроскопист Йоханесс Ридберг (1854 -1919): серия Лаймана серия Бальмера серия Пашена серия Брэккета серия Пфунда RH – постоянная Ридберга RH = 109737. 309 0. 012 cм-1 12

Закономерности в спектре излучения атома водорода 1913: датский физик Нильс Бор cкомбинировал идеи: • квантовой теории Планка, • концепции фотона Эйнштейна, • планетарной модели атома Резерфорда, • ньютоновской механики. 13

Закономерности в спектре излучения атома водорода Основные идеи (постулаты) теории Бора: 1) Электрон движется по круговым орбитам вокруг протона под действием электрической силы притяжения. 2) Только определенные орбиты электронов являются стабильными. Находясь на одной из этих стационарных орбит, электрон не излучает энергию. 3) Излучение испускается атомом при переходе электрона с начальной орбиты c большей энергией на конечную орбиту с меньшей энергией. 4) Разрешены только те орбиты электронов, для которых орбитальный момент импульса относительно ядра квантуется и равен целому множителю ħ=h/2 , mevr = nħ n = 1, 2, 3, … 14

Закономерности в спектре излучения атома водорода Закон сохранения энергии Ei - Ef = hf, Ei – энергия исходного состояния, Ef – энергия конечного состояния, Ei > Ef. Поглощение фотона атомом лишь если энергия фотона hf =Ei - Ef. Исчезновение фотона после поглощения, переход атома на более высокий энергетический уровень. Следствие: характеристический дискретный эмиссионный линейчатый спектр, а также соответствующий линейчатый спектр поглощения. 15

Закономерности в спектре излучения атома водорода Четыре постулата разрешенные уровни энергии и длины волн, испущенных атомом водорода Общая энергия атома Кинетическая энергия электрона Второй закон Ньютона Общая энергия атома Общая энергия связанной системы «электрон-протон» отрицательна. 16

Закономерности в спектре излучения атома водорода Радиусы орбит электронов mevr = nħ 17

Закономерности в спектре излучения атома водорода Орбита с наименьшим радиусом (боровским радиусом) Общее выражение для радиусов произвольных орбит Предсказанные значения достаточно хорошо совпадают с экспериментальными результатами. 18

Закономерности в спектре излучения атома водорода Квантование радиусов орбит приводит к квантованию энергии. Общая энергия атома Радиус произвольной орбиты 19

Закономерности в спектре излучения атома водорода Диаграмма энергетических уровней Е(э. В) n=1 E 1 = - 13, 606 э. В. n=2 Наименьший энергетический уровень E 2 = - 3, 401 э. В …. . …………… n = соответствует r = и E = 0 э. В. Серия Пашена Энергия Серия Бальмера Серия Лаймана Энергия ионизации атома водорода минимальная энергия для полного удаления атома из сферы влияния протона. Расчетное значение равно 13, 6 э. В (совпадает с экспериментальным значением). 20

Закономерности в спектре излучения атома водорода равна экспериментально определенной постоянной Ридберга RH=1, 0973732 107 м-1. Теория Бора: возможность объяснить появление всех серий линий, наблюдаемых в спектрах атома водорода. 21

Закономерности в спектре излучения атома водорода Затруднения теории Бора: 1) Многие линии в серии Бальмера и других сериях вовсе не являются синглетами. Каждая из линий - группа линий, очень тесно расположенных рядом друг с другом (прецизионные спектроскопические измерения). 2) В некоторых случаях при помещении атомов в сильное магнитное поле определенные одиночные спектральные линии расщепляются на три близко расположенные линии. 22

Квантовая модель атома водорода Полностью квантовая модель, базирующаяся на уравнении Шредингера, преодоление затруднений теории Бора. Функция потенциальной энергии для атома водорода 3 D случай: для нахождения волновых функций необходимо найти соответствующие решения уравнения Шредингера 23

Квантовая модель атома водорода Замена прямоугольной системы отсчета на сферическую для учета симметрии атома и упрощения рассмотрения вопроса. Волновая функция Необходимость решить три уравнения: одно для R(r), одно для f( ), одно для g( ). Каждое из решений этих уравнений должно удовлетворять граничным условиям. Например, R(r) должно оставаться конечным при r = 0 и r = , g( ) = g( + 2 ). 24

Квантовые числа и их физический смысл Три различных квантовых числа, характеризующих каждое из разрешенных состояний атома водорода, результат применения граничных условий ко всем трем волновым функциям. Квантовые числа – только целые и соответствуют трем независимым степеням свободы (трехмерное пространство). 25

Квантовые числа и их физический смысл Главное квантовое число n - ассоциация с радиальной функцией R(r). Радиальная функция - отражение вероятности обнаружения электрона на определенном радиальном расстоянии от ядра. Зависимость функции потенциальной энергии только от радиальной координаты r и ни от одной из угловых координат Полное согласие с теорией Бора. 26

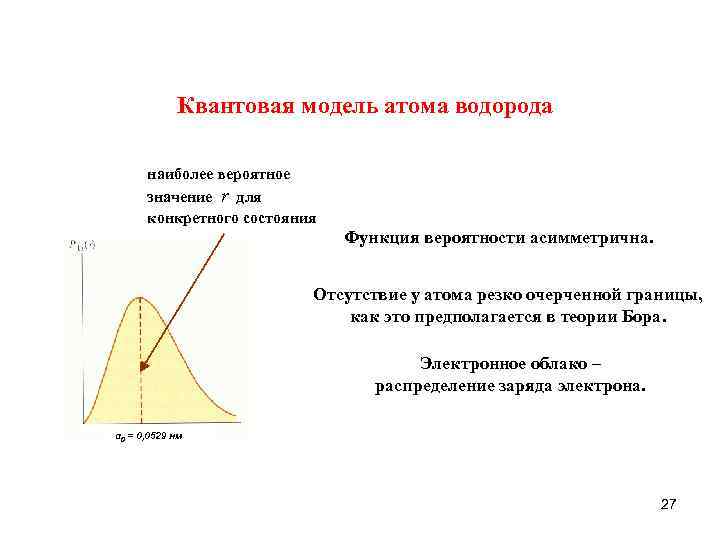Квантовая модель атома водорода наиболее вероятное значение r для конкретного состояния Функция вероятности асимметрична. Отсутствие у атома резко очерченной границы, как это предполагается в теории Бора. Электронное облако – распределение заряда электрона. α 0 = 0, 0529 нм 27

Квантовые числа и их физический смысл Ассоциация орбитального квантового числа l и орбитального магнитного квантового числа ml с орбитальным моментом импульса L электрона. Из граничных условий применительно к значениям волновой функции: n может изменяться от 1 до , l может изменяться от 0 до n – 1, ml может изменяться от - l до l. 28

Квантовые числа и их физический смысл Электронная оболочка: все состояния, имеющие одинаковые n. Подоболочка: все состояния, имеющие одинаковые значения n и l. Обозначения электронных оболочек и подоболочек Символ оболочки Состояние Символ подоболочки 3 p - n = 3 2 s - n = 2 и и l = 1. l = 0. 29

Квантовые числа и их физический смысл Орбитальное квантовое число l Классическая физика: орбитальный момент импульса электрона L может иметь произвольное значение. Боровская модель атома: L = nħ. Квантовая механика: у атома в состоянии с основным квантовым числом n следующие возможные дискретные значения L: 30

Квантовые числа и их физический смысл Орбитальное магнитное квантовое число ml Соответствие дискретных направлений квантованным значениям L. Возможность для Lz принимать только дискретные значения. Пространственное квантование – квантование возможных ориентаций L по отношению к внешнему магнитному полю. 31

- l ml l Квантовые числа и их физический смысл Орбитальное магнитное квантовое число ml Векторная модель, описывающая пространственное квантование для l = 2. L никогда не располагается параллельно или антипараллельно к B, потому что Lz д. б. < L. Для Lz = 0, L д. б. к B. 32

Квантовые числа и их физический смысл Орбитальное магнитное квантовое число ml Принцип неопределенности: отсутствие у L определенного направления, даже если его компонента вдоль оси z зафиксирована. Расположение L где-то на поверхности конуса под углом к оси z. квантуется, т. к. L квантуется. ml никогда не превышает l, и, следовательно, никогда 0. 33

Квантовые числа и их физический смысл Спиновое магнитное квантовое число ms Эксперимент: одна заметная линия в эмиссионном спектре натрия фактически является двумя, близко расположенными линиями, называемыми дублетом. Классическая физика: объяснение отсутствует. 34

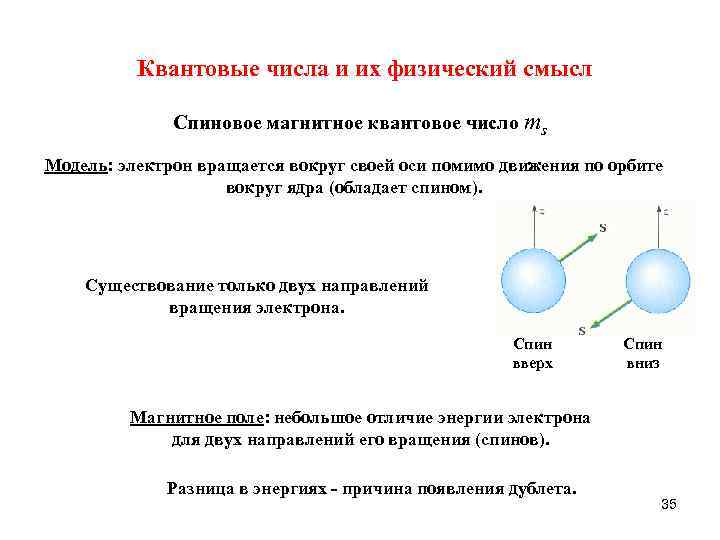Квантовые числа и их физический смысл Спиновое магнитное квантовое число ms Модель: электрон вращается вокруг своей оси помимо движения по орбите вокруг ядра (обладает спином). Существование только двух направлений вращения электрона. Спин вверх Спин вниз Магнитное поле: небольшое отличие энергии электрона для двух направлений его вращения (спинов). Разница в энергиях - причина появления дублета. 35

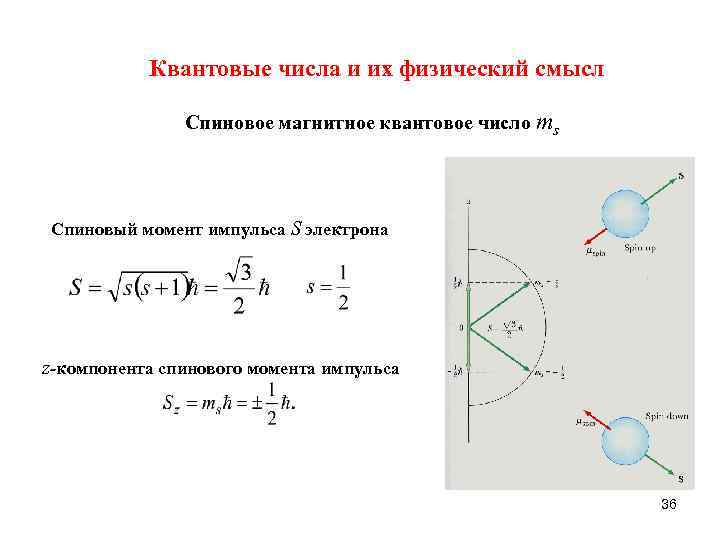Квантовые числа и их физический смысл Спиновое магнитное квантовое число ms Спиновый момент импульса S электрона z-компонента спинового момента импульса 36

Принцип Паули Возможность описать состояние электрона в атоме с помощью четырех квантовых чисел: n, l, ml и ms. Соответствие разных наборов из четырех квантовых чисел всем возможным состояниям электронов в многоэлектронном атоме. 1925: Австрийский физик Вольфганг Паули (1900 -1958) открытие принципа исключительности: электроны в атоме могут находиться только в различных квантовых состояниях. Никакие два электрона в одном и том же атоме не могут обладать одним и тем же набором квантовых чисел. 37

Принцип Паули Электронная структура сложных атомов – последовательность заполненных оболочек, расположенных в порядке нарастания энергии. n - характеристика оболочки. n и l – характеристика подоболочки. Порядок заполнения оболочек в атоме: попадание следующего электрона по мере заполнения оболочки на располагающуюся выше вакантную оболочку с минимальной из возможных энергией. 38

Принцип Паули Атомная орбиталь - набор квантовых чисел n, l и ml. Принцип исключительности - на любой из орбиталей могут находиться только два электрона с ms = + 1/2 и ms = - 1/2. Число электронов, которые могут располагаться в различных оболочках (K, L, M, …) с разными n также ограничено. 39

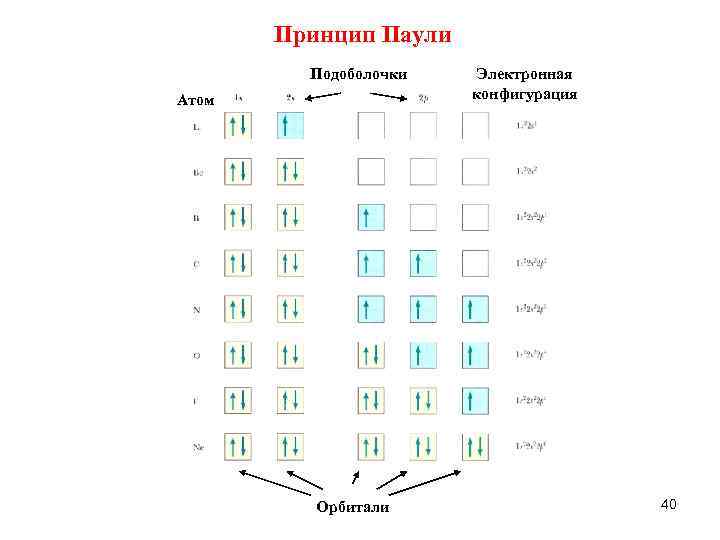Принцип Паули Подоболочки Атом Орбитали Электронная конфигурация 40

Контрольный вопрос Число возможных подоболочек для оболочки с n = 4 в атоме водорода равно (a) 5 (б) 4 (в) 2 (г) 1. 41