Содержание предыдущей лекции Колебательные и волновые процессы Гармонические

Содержание предыдущей лекции Колебательные и волновые процессы Гармонические колебания и их характеристики. Идеальный гармонический осциллятор. Уравнение колебаний идеального осциллятора и его решение. Свободные, затухающие, вынужденные механические и электромагнитные колебания. Волновое движение. Длина волны, волновое число, фазовая скорость. Волновое уравнение. Энергетические характеристики механических и электромагнитных волн. 1

Контрольный вопрос В э-м волне величина вектора напряженности электрического поля по сравнению с величиной вектора напряженности магнитного поля: (a) больше (б) меньше (в) их величины равны. а) 2

Содержание сегодняшней лекции Волновая оптика Интерференция и дифракция света Понятие о когерентности. Понятие об интерференции света. Условия максимумов и минимумов интерференции. Способы наблюдения интерференции. Принцип Гюйгенса-Френеля. Метод зон Френеля. Дифракция Френеля и Фраунгофера. Дифракционная решетка. 3

Волновая оптика 4

Интерференция света 5

Явление интерференции Интерференция – результат суперпозиции (наложения) отдельных волн в одном и том же месте пространства и создания результирующей волны. 6

Явление интерференции Волновое поле, созданное одиночным колеблющимся точечным источником Волновое поле, созданное двумя колеблющимися точечными источниками 7

Условия интерференции • источники света должны быть когерентными – между эмитированными ими волнами света должна поддерживаться постоянная разность фаз; • источники должны быть монохроматическими – эмитированные ими волны должны иметь одинаковую длину волны. 8

Интерференционная картина от двух источников Одиночный протяженный источник света – препятствие со щелями делит исходную волну на две части. Общий способ получения двух когерентных источников света. 9

Интерференционная картина от двух источников 1801: Томас Юнг – первая демонстрация интерференции световых волн от двух источников (эксперимент Юнга с двумя щелями). Интерференционная картина от двух параллельных щелей – яркие и темные параллельные полосы. Барьер Экран Интерференционная картина - результат комбинации (суперпозиции, наложения) э-м полей взаимодействующих световых волн. 10

Интерференционная картина от двух источников Slits Щели S 1 S 2 Светлая полоса Темная полоса Экран 11

Интерференционная картина от двух источников Экран Разность хода 12

Интерференционная картина от двух источников Условие максимумов: =d sin макс= mλ (m = 0, ± 1, ± 2, …) Условие минимумов: =d sin мин= (m+1/2)λ (m = 0, ± 1, ± 2, …) 13

Интерференция в тонких пленках Интерференционные эффекты часто наблюдаются на поверхности тонких пленок масла на воде или тонкого мыльного пузыря. Радужная картина – результат интерференции волн, составляющих белый свет и отраженных от обеих поверхностей тонкой пленки. 14

Интерференция в тонких пленках Воздух Пленка Воздух n 1 Интерференция в лучах отраженного света – результат суперпозиции лучей 1 и 2, отраженных от верхней и нижней поверхностей пленки. n 2 n 1 Интерференция в лучах прошедшего света – результат суперпозиции лучей 3 и 4, прошедших через тонкую пленку. 15

Интерференция в тонких пленках Предположение: лучи света, распространяющиеся в воздухе, практически перпендикулярны к обеим поверхностям пленки. 180 изменение фазы Изменения фазы нет Воздух n 1 Пленка Воздух n 2 • фаза изменяется на 180 при отражении от пленки в случае, когда n 2>n 1, изменения фазы не происходит, когда n 2<n 1; • длина волны света в среде λn=λ/n, где λ – длина волны света в вакууме и n – показатель преломления среды. n 1 16

180 изменение фазы Изменения фазы нет Воздух Пленка Интерференция в тонких пленках Воздух Причины появления разности фаз между отраженными лучами 1 и 2: 1) луч 1 – 180 изменение фазы эквивалентно разности хода λn/2; луч 2 – изменения фазы нет, благодаря разнице в граничных условиях на отражающих поверхностях; 2) дополнительная разность фаз возникает в результате дополнительной дистанции 2 t, пройденной лучом 2 в среде. Вывод: если 2 t = λn/2, то лучи 1 и 2 рекомбинируют в фазе. 17

Интерференция в тонких пленках Отраженные лучи 1 и 2: Условие для конструктивной интерференции (максимумов) 2 t =(m+1/2) λn, (m = 0, 1, 2, …). Условие для деструктивной интерференции (минимумов) 2 nt =mλ, (m = 0, 1, 2, …). 2 nt =(m+1/2) λ, (m = 0, 1, 2, …). 18

Интерференция в тонких пленках Неотражающие покрытия Повышение оптической силы линз – несколько покрытий, имеющих различную толщину. Цель: уменьшить потери света в результате отражения световых волн с различной длиной волны. 19

Дифракция света 20

Дифракция – любое отклонение направления распространения волны света вблизи препятствия от законов геометрической оптики. 21

Принцип Гюйгенса-Френеля (1678): Принцип Гюйгенса – геометрическое построение, основанное на использовании информации о форме и положении фронта волны в предыдущий момент времени для его построения в последующий момент времени. Старый фронт волны Новый фронт волны 22

Метод зон Френеля Френель – дополнение принципа Гюйгенса идеей интерференции вторичных волн и придание ему физического смысла. 23

Метод зон Френеля Замена источника S воображаемыми источниками, расположенными на вспомогательной поверхности Ф – поверхности фронта сферической волны, идущей из S. Кольцевые зоны такого размера, чтобы расстояния от краев зоны до точки М на экране отличались на /2. 24

Метод зон Френеля Точка М: колебания от соседних зон проходят расстояния, отличающиеся на /2. P 1 M – P 0 M = P 2 M – P 1 M = P 3 M – P 2 M =. . . = /2 Колебания от соседних зон приходят в точку М в противоположной фазе. Амплитуда результирующего светового колебания в точке М где А 1, А 2, . . . - амплитуды колебаний, возбуждаемых 1 -й, 2 -й, . . . , m-й зонами. 25

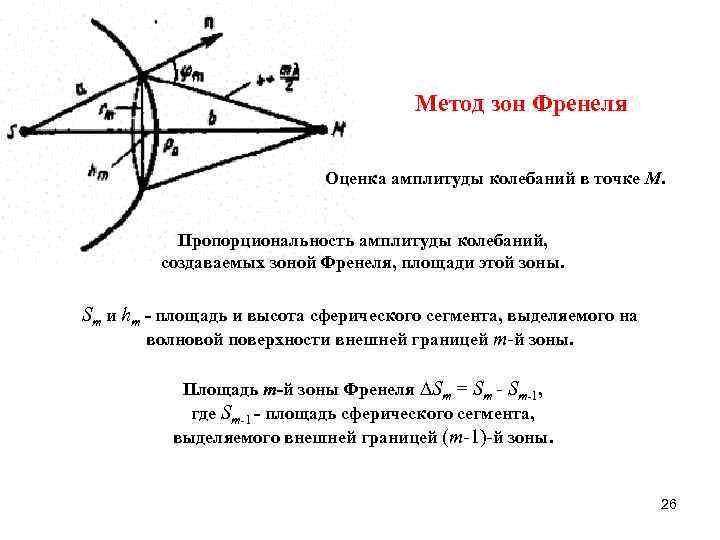
Метод зон Френеля Оценка амплитуды колебаний в точке М. Пропорциональность амплитуды колебаний, создаваемых зоной Френеля, площади этой зоны. Sm и hm - площадь и высота сферического сегмента, выделяемого на волновой поверхности внешней границей m-й зоны. Площадь m-й зоны Френеля Sm = Sm - Sm-1, где Sm-1 - площадь сферического сегмента, выделяемого внешней границей (m-1)-й зоны. 26

Метод зон Френеля Sm не зависит от m. Одинаковая площадь зон Френеля. 27

Метод зон Френеля Больше угол m меньше действие отдельных зон Френеля в точке М. Постепенное убывание действия зон Френеля в направлении от центральной (около Р 0) к периферическим. Уменьшение интенсивности излучения в направлении точки М с ростом m вследствие увеличения расстояния от зоны до точки М. А 1 > А 2 > А 3 > А 4 >…. 28

Метод зон Френеля Большое количество зон Френеля, умещающихся на полусфере. Можно считать, что Малой величиной А /2 пренебрегаем. Амплитуда результирующих колебаний в произвольной точке М определяется как бы действием только половины центральной зоны Френеля 29

Дифракция Френеля на круглом отверстии Зависимость вида дифракционной картины от числа зон Френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке В всеми m зонами, 30

Дифракция Френеля на круглом отверстии Нечетное число зон Френеля – амплитуда (интенсивность) в точке В больше, чем при свободном распространении волны. Четное число зон Френеля - амплитуда (интенсивность) в точке В равна нулю. 31

Дифракция Френеля на диске Исключение закрытого диском участка волнового фронта из рассмотрения. Построение зон Френеля начиная с краев диска. Диском закрыто т первых зон Френеля: 32

Дифракция Френеля на диске Центр дифракционной картины - интерференционный максимум (светлое пятно), соответствующий половине действия первой открытой зоны Френеля. Концентрические темные и светлые интерференционные кольца вокруг основного максимума. Убывание интенсивности в максимумах с расстоянием от центра картины. 33

Дифракция Френеля на диске Большие размеры диска: - за диском тень, вблизи границ которой имеет место весьма слабая дифракционная картина, - можно считать свет распространяющимся прямолинейно. 34

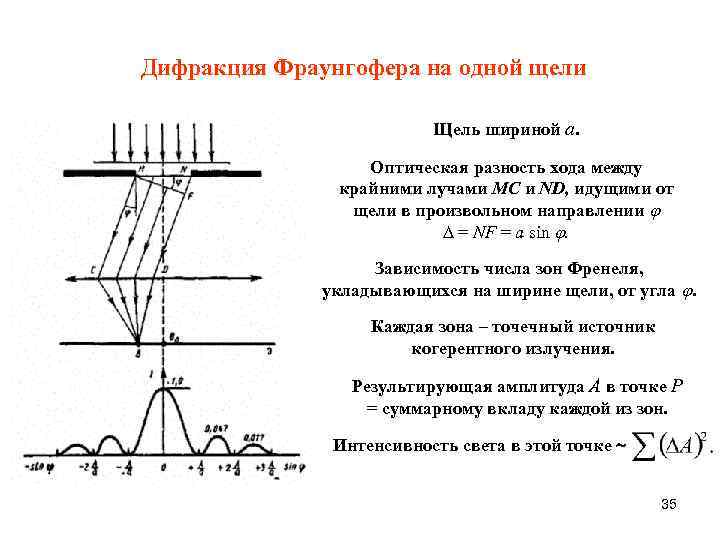
Дифракция Фраунгофера на одной щели Щель шириной а. Оптическая разность хода между крайними лучами МС и ND, идущими от щели в произвольном направлении = NF = a sin . Зависимость числа зон Френеля, укладывающихся на ширине щели, от угла . Каждая зона – точечный источник когерентного излучения. Результирующая амплитуда A в точке P = суммарному вкладу каждой из зон. Интенсивность света в этой точке 35

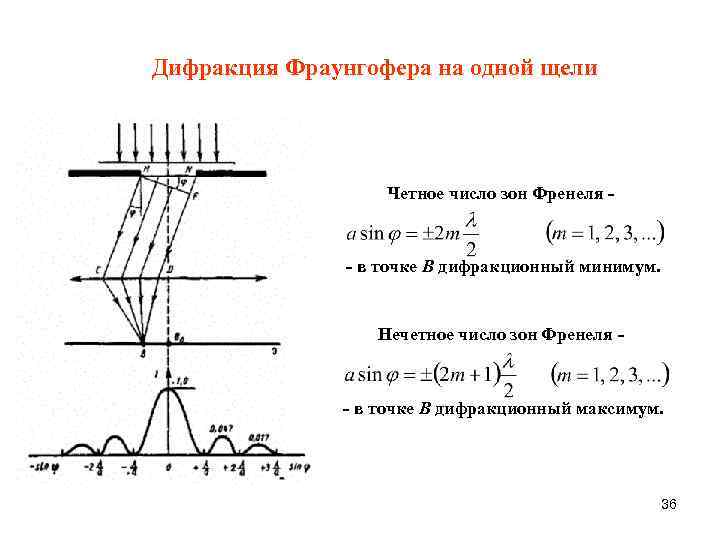
Дифракция Фраунгофера на одной щели Четное число зон Френеля - - в точке В дифракционный минимум. Нечетное число зон Френеля - - в точке В дифракционный максимум. 36

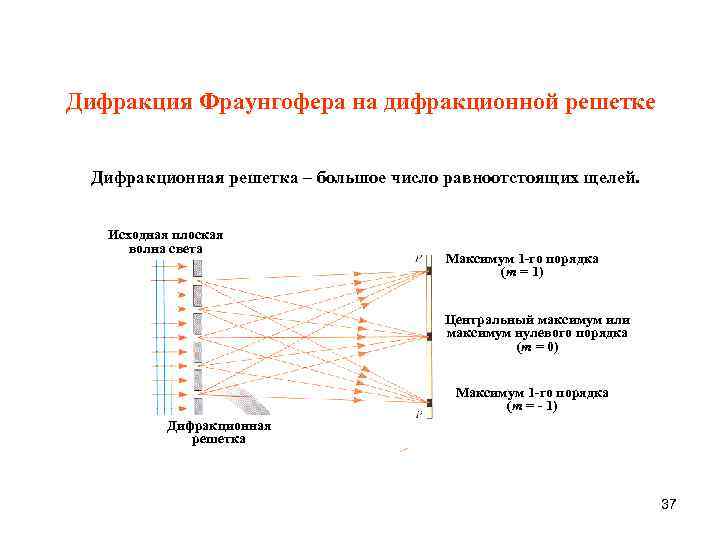
Дифракция Фраунгофера на дифракционной решетке Дифракционная решетка – большое число равноотстоящих щелей. Исходная плоская волна света Максимум 1 -го порядка (m = 1) Центральный максимум или максимум нулевого порядка (m = 0) Максимум 1 -го порядка (m = - 1) Дифракционная решетка 37

Дифракция Фраунгофера на дифракционной решетке Одинаковая фаза волн у щелей. Разное расстояние, проходимое волнами от щелей до точки на экране. Условия для появления интерференционных максимумов 38

Дифракция Фраунгофера на дифракционной решетке Распределение интенсивности дифрагировавших лучей Основные максимумы острые, минимумы широкие. Увеличение числа щелей: - уменьшение ширины максимумов, - увеличение яркости максимумов. 39

Дифракционная решетка Компакт-диск - дифракционная решетка. 40

Контрольный вопрос a Если уменьшить ширину щели на рисунке вдвое, то ширина центрального максимума (a) увеличится, (б) останется неизменной, (в) уменьшится. 41