Скачать презентацию СОДЕРЖАНИЕ 1 Физика-наука о природе 2 Раздел 1 Скачать презентацию СОДЕРЖАНИЕ 1 Физика-наука о природе 2 Раздел 1

Кинематика.ppt

  • Количество слайдов: 56

СОДЕРЖАНИЕ 1. Физика-наука о природе. 2. Раздел 1. Механика. 3. Тема 1. 1. Кинематика СОДЕРЖАНИЕ 1. Физика-наука о природе. 2. Раздел 1. Механика. 3. Тема 1. 1. Кинематика твёрдого тела: - механическое движение; -относительность механического движения. Системы отсчёта; -характеристики механического движения; -виды движения и их графическое описание;

СОДЕРЖАНИЕ (продолжение) -движение по окружности с постоянной по модулю скоростью. 4. Закрепление. 5. Решение СОДЕРЖАНИЕ (продолжение) -движение по окружности с постоянной по модулю скоростью. 4. Закрепление. 5. Решение задач. 6. Задачи на дом.

ФИЗИКАодна из наук о природе. Физика- наука о строении материи и о простейших формах ФИЗИКАодна из наук о природе. Физика- наука о строении материи и о простейших формах её движения и взаимодействия.

Физика – одна из древнейших наук. С древних времён люди искали ответы на вопросы: Физика – одна из древнейших наук. С древних времён люди искали ответы на вопросы: почему светится Солнце? Отчего возникают северные полярные сияния? Как возникает молния? Почему извергается вулкан? И еще много других. вопросов.

Все науки начались с ФИЗИКИ, ибо ФИЗИКА начало всех начал, т. е. природа. Все Все науки начались с ФИЗИКИ, ибо ФИЗИКА начало всех начал, т. е. природа. Все новые науки о природе-химия, биология, экология, геология, астрономия и другие выделились из физики.

Теснейшая связь физики с другими отраслями естествознания привела к тому, что образовался ряд новых Теснейшая связь физики с другими отраслями естествознания привела к тому, что образовался ряд новых смежных дисциплин, таких, как астрофизика, геофизика, физическая химия, биофизика и др.

С помощью физики можно и нужно познавать мир, т. к. познание мира – это С помощью физики можно и нужно познавать мир, т. к. познание мира – это движение вперёд.

Не сломай мозг! Не сломай мозг!

РАЗДЕЛ 1. МЕХАНИКА РАЗДЕЛ 1. МЕХАНИКА

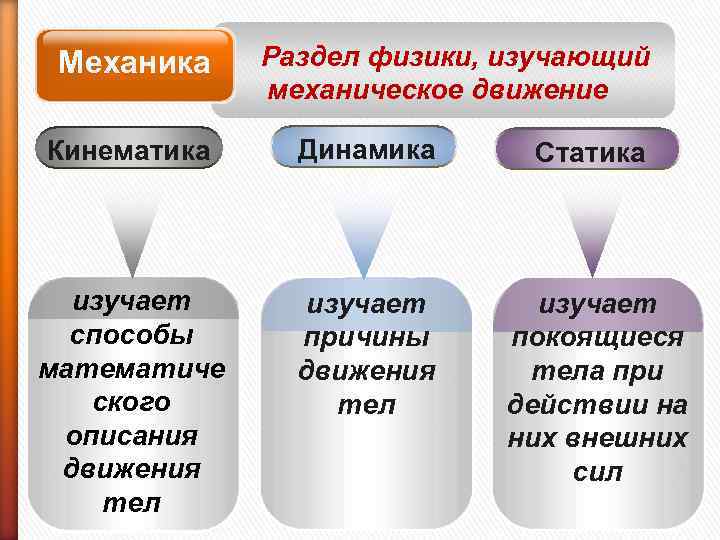Механика Раздел физики, изучающий механическое движение Кинематика Динамика Статика изучает способы математиче ского описания Механика Раздел физики, изучающий механическое движение Кинематика Динамика Статика изучает способы математиче ского описания движения тел изучает причины движения тел изучает покоящиеся тела при действии на них внешних сил

ТЕМА 1. 1. Кинематика твёрдого тела ТЕМА 1. 1. Кинематика твёрдого тела

Механическим движением называется процесс изменения положения тела в пространстве относительно других тел с течением Механическим движением называется процесс изменения положения тела в пространстве относительно других тел с течением времени. Линия, вдоль которой движется точка тела, называется траекторией движения. Траектория движения - это воображаемая линия, хотя, если тело при движении оставляет за собой след, ее можно увидеть.

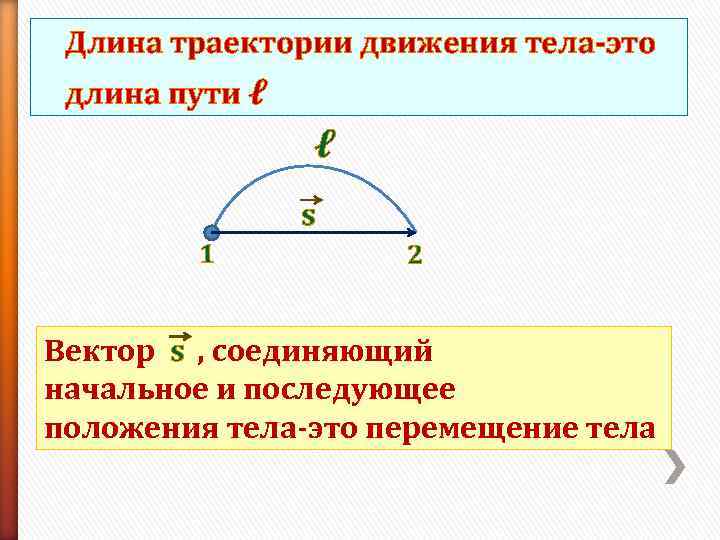Длина траектории движения тела-это длина пути ℓ ℓ s 1 2 Вектор s , Длина траектории движения тела-это длина пути ℓ ℓ s 1 2 Вектор s , соединяющий начальное и последующее положения тела-это перемещение тела

Тело можно рассматривать как материальную точку, если его размеры малы по сравнению с расстоянием, Тело можно рассматривать как материальную точку, если его размеры малы по сравнению с расстоянием, которое оно проходит, или по сравнению с расстоянием от него до других тел. Пример. Размеры орбитальной станции, находящейся на орбите около Земли, можно не учитывать, а рассчитывая траекторию движения космического корабля при стыковке со станцией, без учета ее размеров не обойтись.

2. Относительность механического движения. Системы отсчёта. 2. Относительность механического движения. Системы отсчёта.

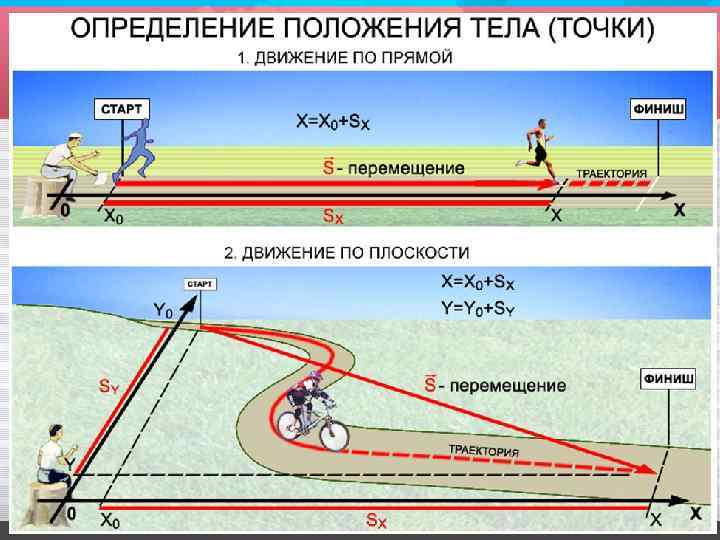
Механическое движение относительно, выражение «тело движется» лишено всякого смысла, пока не определено, относительно чего Механическое движение относительно, выражение «тело движется» лишено всякого смысла, пока не определено, относительно чего рассматривается движение. Для определения положения материальной точки в любой момент времени следует выбрать: Тело отсчета Система координат Часы ТЕЛО ОТСЧЁТА - это тело, относительно которого определяется положение других (движущихся) тел.

Системы координат Ø Координатная прямая х y Примеры: лифт, метро трамвай. х Ø Координатная Системы координат Ø Координатная прямая х y Примеры: лифт, метро трамвай. х Ø Координатная плоскость шахматы, Ø Пространственная система координат клад, люстра, y z x

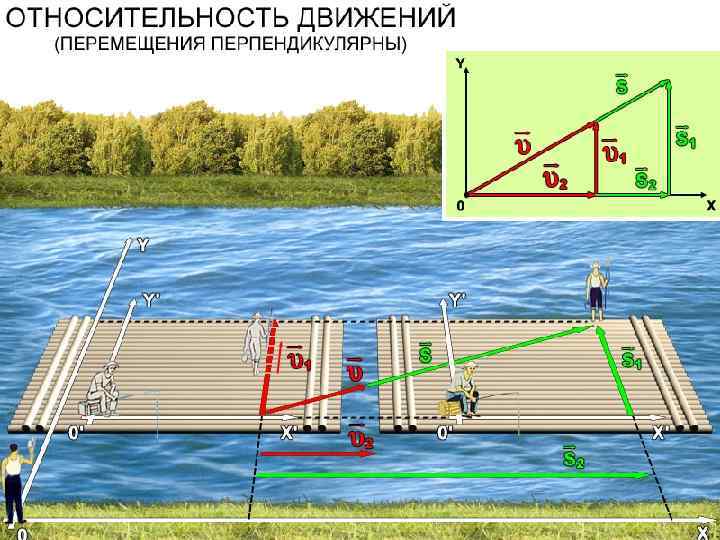
Относительность траектории движения Относительность траектории движения

Но наряду с относительностью механическому движению присущи и черты абсолютности. Абсолютными называют такие свойства Но наряду с относительностью механическому движению присущи и черты абсолютности. Абсолютными называют такие свойства движения, которые не зависят от выбора тела отсчета. Например, если относительно Земли два тела А и В приближаются друг к другу, то их сближение будет происходить и относительно любого другого тела отсчета (автомобиля, Луны, Солнца и т. д. ). Другими словами, нельзя найти такое тело отсчета, по отношению к которому эти два тела А и В не сближались бы, а, например, удалялись бы друг от друга. Сближение этих тел имеет абсолютный характер.

3. Характеристики механического движения 3. Характеристики механического движения

Механическое движение характеризуется тремя физическими величинами: перемещением, скоростью и ускорением. Направленный отрезок прямой, проведенный Механическое движение характеризуется тремя физическими величинами: перемещением, скоростью и ускорением. Направленный отрезок прямой, проведенный из начального положения движущейся точки в ее конечное положение, называется перемещением ( ). Перемещение — величина векторная. Единица перемещения — метр.

Скорость — векторная физическая величина, характеризующая быстроту перемещения тела, численно равная отношению перемещения за Скорость — векторная физическая величина, характеризующая быстроту перемещения тела, численно равная отношению перемещения за малый промежуток времени к величине этого промежутка. Промежуток времени считается достаточно малым, если скорость при неравномерном движении в течение этого промежутка не менялась. Формула мгновенной скорости имеет вид. Единица скорости в СИ — м/с. На практике используют единицу измерения скорости км/ч (36 км/ч = 10 м/с). Измеряют скорость спидометром.

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло. Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле: Единица ускорения Ускорение измеряют акселерометром.

Характеристики механического движения связаны между собой основными кинематическими уравнениями: Если тело движется без ускорения, Характеристики механического движения связаны между собой основными кинематическими уравнениями: Если тело движется без ускорения, то его скорость в течение продолжительного времени не меняется, а = 0, тогда кинематические уравнения будут иметь вид:

4. Виды движения и их графическое описание. 4. Виды движения и их графическое описание.

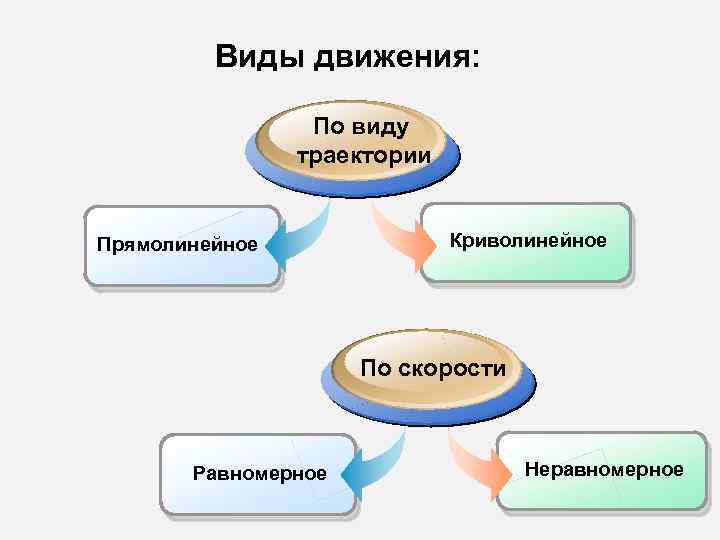Виды движения: По виду траектории Прямолинейное Криволинейное По скорости Равномерное Неравномерное Виды движения: По виду траектории Прямолинейное Криволинейное По скорости Равномерное Неравномерное

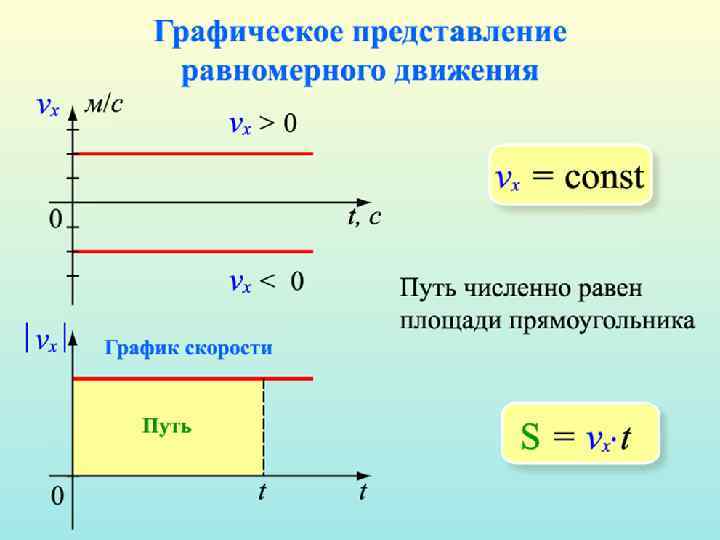
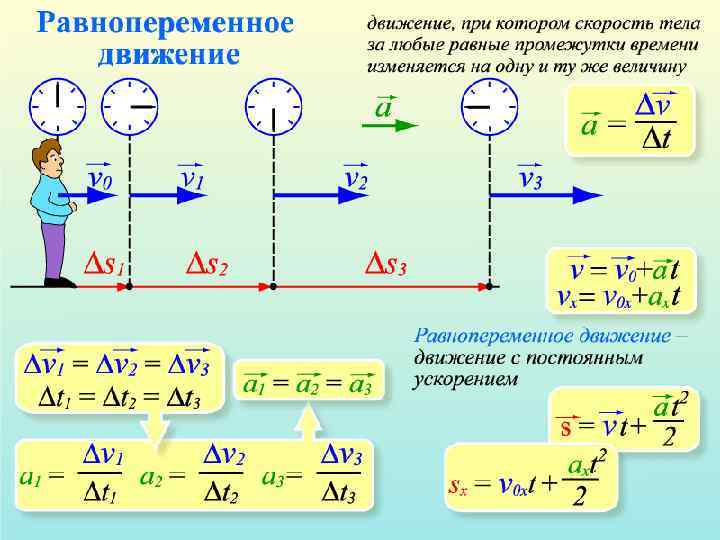
Если скорость и ускорение тела имеют одинаковые направления (а>0), то такое равнопеременное движение называется Если скорость и ускорение тела имеют одинаковые направления (а>0), то такое равнопеременное движение называется равноускоренным. В этом случае кинематические уравнения выглядят так:

Если скорость и ускорение тела имеют противоположные направления (а<0), то такое равнопеременное движение называется Если скорость и ускорение тела имеют противоположные направления (а<0), то такое равнопеременное движение называется равнозамедленным. В этом случае кинематические уравнения выглядят так:

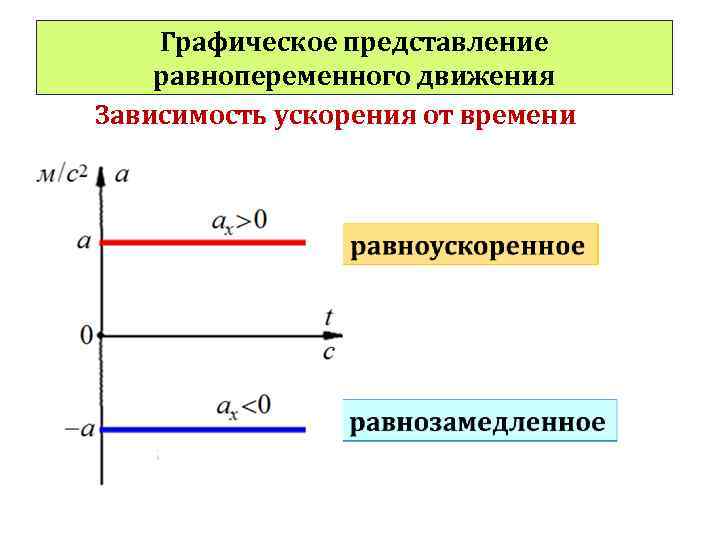Графическое представление равнопеременного движения Зависимость ускорения от времени Графическое представление равнопеременного движения Зависимость ускорения от времени

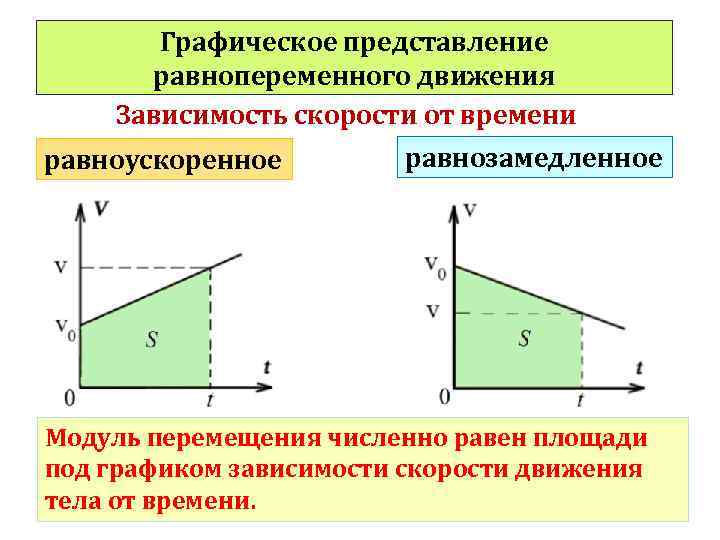Графическое представление равнопеременного движения Зависимость скорости от времени равноускоренное равнозамедленное Модуль перемещения численно равен Графическое представление равнопеременного движения Зависимость скорости от времени равноускоренное равнозамедленное Модуль перемещения численно равен площади под графиком зависимости скорости движения тела от времени.

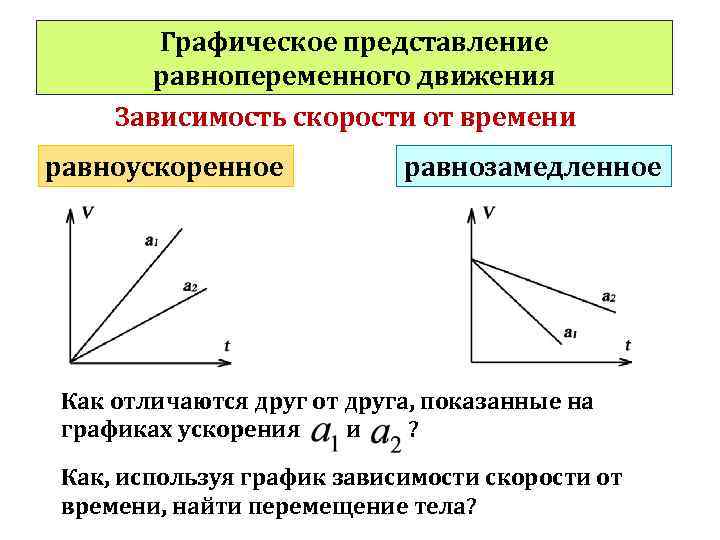Графическое представление равнопеременного движения Зависимость скорости от времени равноускоренное равнозамедленное Как отличаются друг от Графическое представление равнопеременного движения Зависимость скорости от времени равноускоренное равнозамедленное Как отличаются друг от друга, показанные на графиках ускорения и ? Как, используя график зависимости скорости от времени, найти перемещение тела?

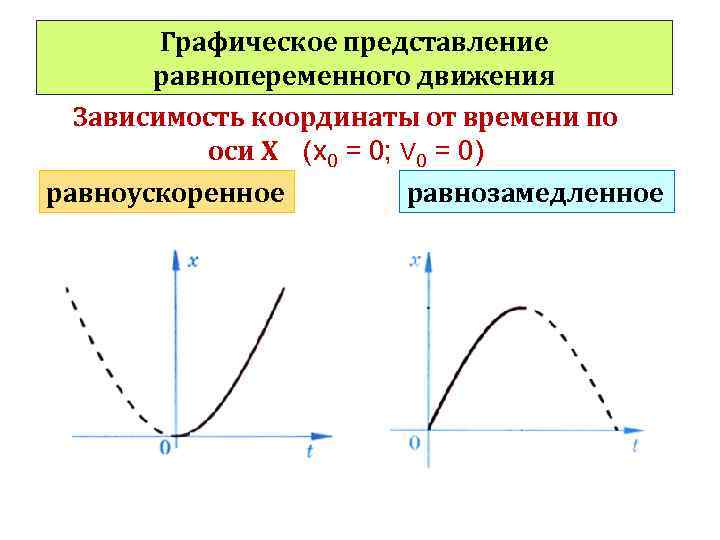Графическое представление равнопеременного движения Зависимость координаты от времени по оси Х (х0 = 0; Графическое представление равнопеременного движения Зависимость координаты от времени по оси Х (х0 = 0; V 0 = 0) равноускоренное равнозамедленное

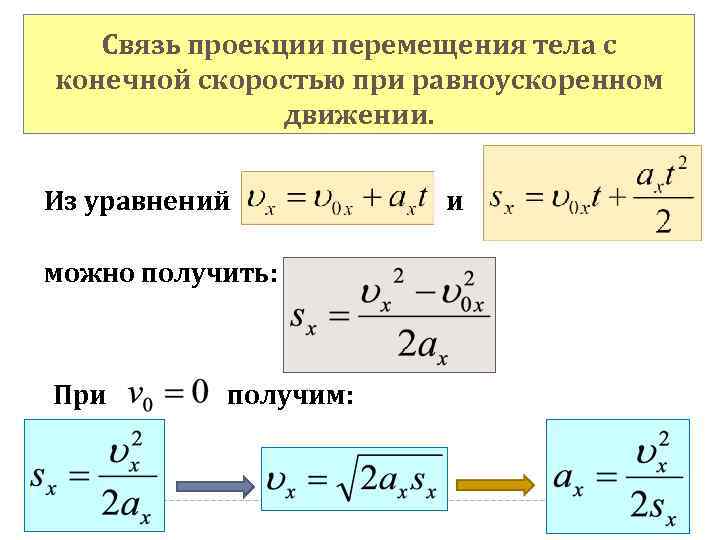Связь проекции перемещения тела с конечной скоростью при равноускоренном движении. Из уравнений можно получить: Связь проекции перемещения тела с конечной скоростью при равноускоренном движении. Из уравнений можно получить: При получим: и

Домашнее задание: Задача 1. Поезд, имея начальную скорость , стал двигаться равнозамедленно и через Домашнее задание: Задача 1. Поезд, имея начальную скорость , стал двигаться равнозамедленно и через время t=10 c скорость до. Какова средняя скорость поезда? С каким ускорением двигался поезд на этом участке? Какой он при этом прошёл путь? ( s ≈170 м) Задача 2. Поезд, двигаясь со станции с ускорением а=0, 4 м/с , прошёл путь s=0, 5 км. Какой скорости достиг при этом поезд и сколько времени он разгонялся? ( υ=20 м/с , t=50 с )

5. Движение по окружности с постоянной по модулю скоростью. 5. Движение по окружности с постоянной по модулю скоростью.

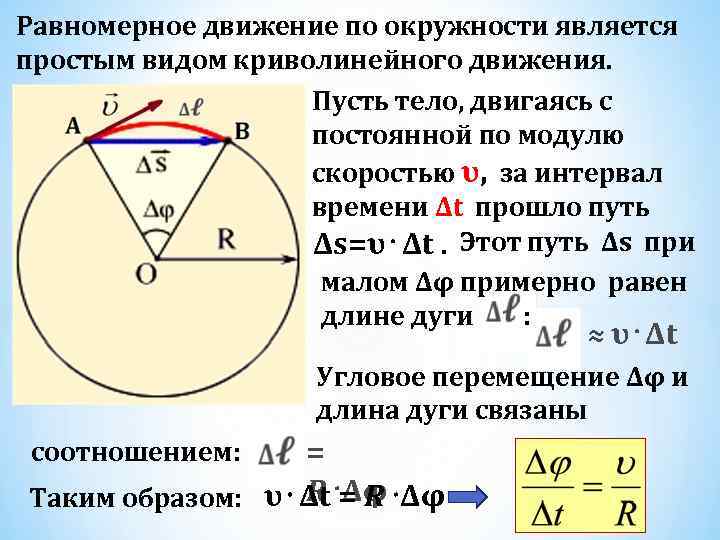Равномерное движение по окружности является простым видом криволинейного движения. Пусть тело, двигаясь с постоянной Равномерное движение по окружности является простым видом криволинейного движения. Пусть тело, двигаясь с постоянной по модулю скоростью υ, за интервал времени Δt прошло путь Δs=υ⋅Δt. Этот путь Δs при малом Δφ примерно равен длине дуги : ≈ υ⋅Δt Угловое перемещение Δφ и длина дуги связаны = R Δφ Таким образом: υ⋅Δt⋅= R⋅Δφ соотношением:

Отношение изменения угла поворота тела Δφ при перемещении по окружности к промежутку времени перемещения Отношение изменения угла поворота тела Δφ при перемещении по окружности к промежутку времени перемещения Δt называется угловой скоростью ω : Таким образом, между линейной скоростью υ и угловой скоростью ω устанавливается связь: или

Промежуток времени, за который тело совершает полный оборот при движении по окружности, называется периодом Промежуток времени, за который тело совершает полный оборот при движении по окружности, называется периодом обращения. Период обращения обозначается буквой Т. За время Δt=Т тело повернётся на угол Δφ=2π и угловая скорость может быть найдена как: Выражение линейной скорости через период обращения имеет вид:

Частота обращения обозначается буквой ν (читается «ню» ) и показывает, сколько оборотов по окружности Частота обращения обозначается буквой ν (читается «ню» ) и показывает, сколько оборотов по окружности совершает тело в единицу времени. Уравнения линейной и круговой скорости через частоту обращения имеют вид:

При равномерном движении по окружности значение скорости (модуль скорости) остаётся постоянным, а направление вектора При равномерном движении по окружности значение скорости (модуль скорости) остаётся постоянным, а направление вектора скорости изменяется в процессе движения. А если скорость изменяется, значит движение по окружности происходит с ускорением. Определим ускорение тела, движущегося равномерно по окружности радиусом R. За время Δt тело проходит путь Δs=υ⋅Δt. Этот путь Δs равен длине дуги АВ. Векторы скоростей и 0 в точках А и В направлены по касательным к окружности в этих точках.

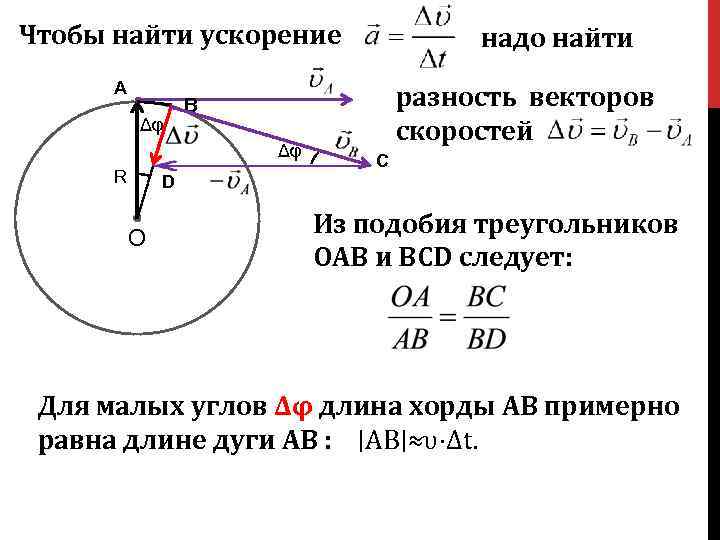Чтобы найти ускорение A Δφ разность векторов скоростей В Δφ R надо найти С Чтобы найти ускорение A Δφ разность векторов скоростей В Δφ R надо найти С D О О Из подобия треугольников ОАВ и ВСD следует: Для малых углов Δφ длина хорды АВ примерно равна длине дуги АВ : ∣AB∣≈υ⋅Δt.

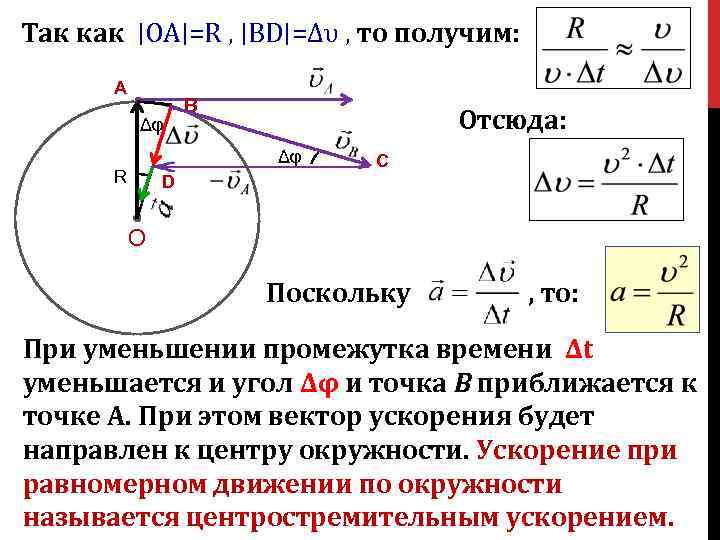Так как ∣OA∣=R , ∣BD∣=Δυ , то получим: A Δφ В Отсюда: Δφ R Так как ∣OA∣=R , ∣BD∣=Δυ , то получим: A Δφ В Отсюда: Δφ R С D О О Поскольку , то: При уменьшении промежутка времени Δt уменьшается и угол Δφ и точка В приближается к точке А. При этом вектор ускорения будет направлен к центру окружности. Ускорение при равномерном движении по окружности называется центростремительным ускорением.

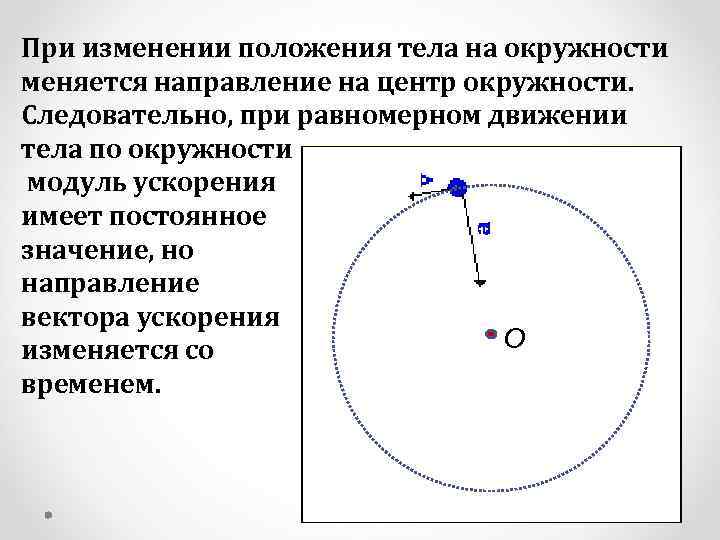При изменении положения тела на окружности меняется направление на центр окружности. Следовательно, при равномерном При изменении положения тела на окружности меняется направление на центр окружности. Следовательно, при равномерном движении тела по окружности модуль ускорения имеет постоянное значение, но направление вектора ускорения О изменяется со временем.

Если ранее полученные выражения скорости через период и частоту обращения подставить в формулу центростремительного Если ранее полученные выражения скорости через период и частоту обращения подставить в формулу центростремительного ускорения , то получим:

Закрепление 1. Механическим движением называется ____ 2. Раздел «Механика» состоит из ________ 3. Кинематика Закрепление 1. Механическим движением называется ____ 2. Раздел «Механика» состоит из ________ 3. Кинематика изучает _____________ 4. Для определения положения тела надо выбрать___ 5. Системы координат бывают __________ 6. Перечислите физические величины, характеризующие механическое движение: 7. Линия, вдоль которой движется тело, называется__ 8. Перемещение - это ______________ 9. Физическая величина, характеризующая быстроту изменения скорости тела, называется _____ 10. Запишите уравнение скорости тела при равноускоренном движении тела с начальной скоростью, отличной от нуля:

Решение задач. 1. Шкив диаметром 20 см делает 300 оборотов за 3 мин. Определить Решение задач. 1. Шкив диаметром 20 см делает 300 оборотов за 3 мин. Определить период вращения , угловую и линейную скорости точки на ободе шкива. Дано: СИ D=20 cм =0, 2 м t=3 мин =180 с N=300 T-? ω-? υ-? Решение. Время одного полного оборота (период вращения): Т=t/N; T=(180 /300)с=0, 6 c Угловая скорость: ω=2π/Т; ω=(2⋅3, 14 /0, 6) рад/ с=10, 5 рад/с Линейная скорость: υ=ωR=ωD/2; υ=(10, 5⋅0, 2/2) м/с=1, 05

2. Минутная стрелка часов на Спасской башне Кремля имеет длину 3, 5 м. На 2. Минутная стрелка часов на Спасской башне Кремля имеет длину 3, 5 м. На сколько передвинется её конец за 1 мин? Дано: СИ Решение. R=3, 5 м Линейная скорость, с которой t=1 мин =60 с перемещается конец стрелки: s-? υ=ωR=2πR/T Период обращения минутной стрелки Т=1 час. Тогда : υ=2πR/T=(2⋅3, 14⋅3, 5/3600) м/с=0, 0061 м/с Искомое передвижение равно: s=υ⋅t; s=(0, 0061⋅60) м=0, 366 м.

Домашнее задание: Задача 1. Поезд, имея начальную скорость , стал двигаться равнозамедленно и через Домашнее задание: Задача 1. Поезд, имея начальную скорость , стал двигаться равнозамедленно и через время t=10 c скорость до. Какова средняя скорость поезда? С каким ускорением двигался поезд на этом участке? Какой он при этом прошёл путь? ( s ≈170 м) Задача 2. Поезд, двигаясь со станции с ускорением а=0, 4 м/с , прошёл путь s=0, 5 км. Какой скорости достиг при этом поезд и сколько времени он разгонялся? ( υ=20 м/с , t=50 с )