Социальное моделирование и прогнозирование (специальность журналистика) Заместитель декана










lektsia_4_zhur-d-5_sots_mod_prog.pptx
- Размер: 293.8 Кб
- Автор:
- Количество слайдов: 24
Описание презентации Социальное моделирование и прогнозирование (специальность журналистика) Заместитель декана по слайдам
 Социальное моделирование и прогнозирование (специальность журналистика) Заместитель декана факультета информационных технологий, доцент кафедры Ми. И к. т. н. Дмитрий Николаевич Скрипка «Российский государственный социальный университет» Москва
Социальное моделирование и прогнозирование (специальность журналистика) Заместитель декана факультета информационных технологий, доцент кафедры Ми. И к. т. н. Дмитрий Николаевич Скрипка «Российский государственный социальный университет» Москва
 Лекция 4 Основные понятия сетевого планирования. Сетевые модели Учебные вопросы: 3. 1. Основные этапы развития сетевого планирования. 3. 2. Основные методы разработки сетевых моделей. 3. 3. Методика построения сетевой модели: 3. 3. 1. Подготовка исходных данных; 3. 3. 2. Правила построения сетевых графиков; 3. 3. 3. Нумерация работ и событий; 3. 3. 4. Временные параметры сетевого графика; 3. 3. 5. Анализ сетевого графика.
Лекция 4 Основные понятия сетевого планирования. Сетевые модели Учебные вопросы: 3. 1. Основные этапы развития сетевого планирования. 3. 2. Основные методы разработки сетевых моделей. 3. 3. Методика построения сетевой модели: 3. 3. 1. Подготовка исходных данных; 3. 3. 2. Правила построения сетевых графиков; 3. 3. 3. Нумерация работ и событий; 3. 3. 4. Временные параметры сетевого графика; 3. 3. 5. Анализ сетевого графика.
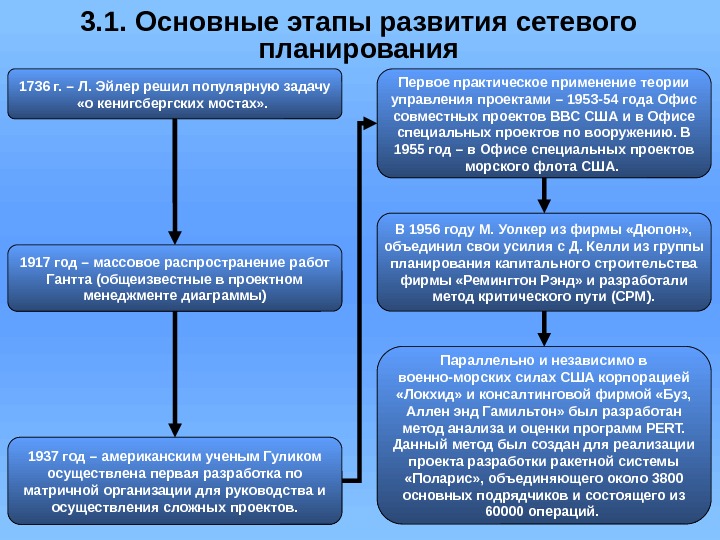
 3. 1. Основные этапы развития сетевого планирования 1736 г. – Л. Эйлер решил популярную задачу «о кенигсбергских мостах» . 1917 год – массовое распространение работ Гантта (общеизвестные в проектном менеджменте диаграммы) 1937 год – американским ученым Гуликом осуществлена первая разработка по матричной организации для руководства и осуществления сложных проектов. Первое практическое применение теории управления проектами – 1953 -54 года Офис совместных проектов ВВС США и в Офисе специальных проектов по вооружению. В 1955 год – в Офисе специальных проектов морского флота США. В 1956 году М. Уолкер из фирмы «Дюпон» , объединил свои усилия с Д. Келли из группы планирования капитального строительства фирмы «Ремингтон Рэнд» и разработали метод критического пути (СРМ). Параллельно и независимо в военно-морских силах США корпорацией «Локхид» и консалтинговой фирмой «Буз, Аллен энд Гамильтон» был разработан метод анализа и оценки программ PERT. Данный метод был создан для реализации проекта разработки ракетной системы «Поларис» , объединяющего около 3800 основных подрядчиков и состоящего из 60000 операций.
3. 1. Основные этапы развития сетевого планирования 1736 г. – Л. Эйлер решил популярную задачу «о кенигсбергских мостах» . 1917 год – массовое распространение работ Гантта (общеизвестные в проектном менеджменте диаграммы) 1937 год – американским ученым Гуликом осуществлена первая разработка по матричной организации для руководства и осуществления сложных проектов. Первое практическое применение теории управления проектами – 1953 -54 года Офис совместных проектов ВВС США и в Офисе специальных проектов по вооружению. В 1955 год – в Офисе специальных проектов морского флота США. В 1956 году М. Уолкер из фирмы «Дюпон» , объединил свои усилия с Д. Келли из группы планирования капитального строительства фирмы «Ремингтон Рэнд» и разработали метод критического пути (СРМ). Параллельно и независимо в военно-морских силах США корпорацией «Локхид» и консалтинговой фирмой «Буз, Аллен энд Гамильтон» был разработан метод анализа и оценки программ PERT. Данный метод был создан для реализации проекта разработки ракетной системы «Поларис» , объединяющего около 3800 основных подрядчиков и состоящего из 60000 операций.
 3. 1. Основные этапы развития сетевого планирования «Технологи- ческие задачи» Управление проектами Модели организа-ци онных структур Модели коллекти-во в и групп. Обменные схемы «Транспорт -ные» задачи Теория Графов «Транспортные» задачи, в которых вершинами графа являются пункты, а ребрами – дороги (автомобильные, железные и др. ) и / или другие транспортные, (авиационные) маршруты. Другой пример – сети снабжения (энергоснабжения, газоснабжения, снабжения товарами и т. п. ). «Технологические задачи» , в которых вершины отражают производственные элементы, цеха, станки и т. п. ), а дуги – потоки сырья, материалов и продукции между ними, заключаются в определении оптимальной загрузки производственных элементов и обеспечивающих эту загрузку потоков. Обменные схемы, являющиеся моделями таких явлений как бартер, взаимозачеты и т. п. Вершины графа при этом описывают участников обменной схемы (цепочки), а дуги – потоки материальных и финансовых ресурсов между ними. Задача заключается в определении оптимальной цепочки обменов, согласованной с существующими ограничениями. Модели коллективов и групп, используемые в социологии, основываются на представлении людей или их групп в виде вершин, а отношений между ними в виде ребер или дуг. В рамках подобного описания решаются задачи исследования структуры социальных групп. Модели организационных структур, в которых вершинами являются элементы организационной системы, а ребрами или дугами – связи (информационные, управляющие, технологические и др. ) между ними. Управление проектами. С точки зрения теории графов проект – совокупность операций и зависимостей между ними Совокупность моделей и методов, использующих язык и результаты теории графов и ориентированных на решение задач управления проектами, получила название календарно-сетевого планирования и управления (КСПУ). Вершина Дуга Ребро. Граф – система, которая интуитивно может быть рассмотрена как множество кружков и множество соединяющих их линий (геометрический способ задания графа – см. рисунок 1). Кружки называются вершинами графа, линии со стрелками – дугами, без стрелок – ребрами. Граф, в котором направление линий не выделяется, (все линии являются ребрами), называется неориентированным; граф, в котором направление линий принципиально (являются дугами) называется ориентированным.
3. 1. Основные этапы развития сетевого планирования «Технологи- ческие задачи» Управление проектами Модели организа-ци онных структур Модели коллекти-во в и групп. Обменные схемы «Транспорт -ные» задачи Теория Графов «Транспортные» задачи, в которых вершинами графа являются пункты, а ребрами – дороги (автомобильные, железные и др. ) и / или другие транспортные, (авиационные) маршруты. Другой пример – сети снабжения (энергоснабжения, газоснабжения, снабжения товарами и т. п. ). «Технологические задачи» , в которых вершины отражают производственные элементы, цеха, станки и т. п. ), а дуги – потоки сырья, материалов и продукции между ними, заключаются в определении оптимальной загрузки производственных элементов и обеспечивающих эту загрузку потоков. Обменные схемы, являющиеся моделями таких явлений как бартер, взаимозачеты и т. п. Вершины графа при этом описывают участников обменной схемы (цепочки), а дуги – потоки материальных и финансовых ресурсов между ними. Задача заключается в определении оптимальной цепочки обменов, согласованной с существующими ограничениями. Модели коллективов и групп, используемые в социологии, основываются на представлении людей или их групп в виде вершин, а отношений между ними в виде ребер или дуг. В рамках подобного описания решаются задачи исследования структуры социальных групп. Модели организационных структур, в которых вершинами являются элементы организационной системы, а ребрами или дугами – связи (информационные, управляющие, технологические и др. ) между ними. Управление проектами. С точки зрения теории графов проект – совокупность операций и зависимостей между ними Совокупность моделей и методов, использующих язык и результаты теории графов и ориентированных на решение задач управления проектами, получила название календарно-сетевого планирования и управления (КСПУ). Вершина Дуга Ребро. Граф – система, которая интуитивно может быть рассмотрена как множество кружков и множество соединяющих их линий (геометрический способ задания графа – см. рисунок 1). Кружки называются вершинами графа, линии со стрелками – дугами, без стрелок – ребрами. Граф, в котором направление линий не выделяется, (все линии являются ребрами), называется неориентированным; граф, в котором направление линий принципиально (являются дугами) называется ориентированным.
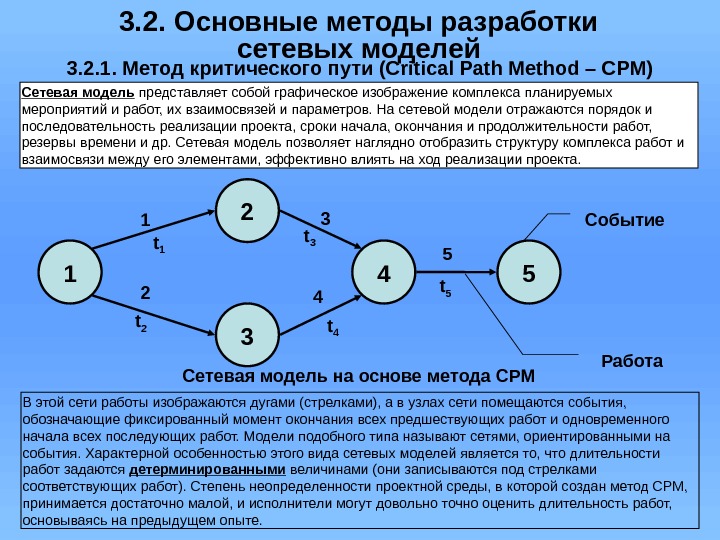
 3. 2. Основные методы разработки сетевых моделей 3. 2. 1. Метод критического пути (Critical Path Method – CPM) Сетевая модель представляет собой графическое изображение комплекса планируемых мероприятий и работ, их взаимосвязей и параметров. На сетевой модели отражаются порядок и последовательность реализации проекта, сроки начала, окончания и продолжительности работ, резервы времени и др. Сетевая модель позволяет наглядно отобразить структуру комплекса работ и взаимосвязи между его элементами, эффективно влиять на ход реализации проекта. В этой сети работы изображаются дугами (стрелками), а в узлах сети помещаются события, обозначающие фиксированный момент окончания всех предшествующих работ и одновременного начала всех последующих работ. Модели подобного типа называют сетями, ориентированными на события. Характерной особенностью этого вида сетевых моделей является то, что длительности работ задаются детерминированными величинами (они записываются под стрелками соответствующих работ). Степень неопределенности проектной среды, в которой создан метод CPM, принимается достаточно малой, и исполнители могут довольно точно оценить длительность работ, основываясь на предыдущем опыте. Сетевая модель на основе метода СРМ 1 1 32 4 5 2 3 4 5 t 1 t 2 t 3 t 4 t 5 Событие Работа
3. 2. Основные методы разработки сетевых моделей 3. 2. 1. Метод критического пути (Critical Path Method – CPM) Сетевая модель представляет собой графическое изображение комплекса планируемых мероприятий и работ, их взаимосвязей и параметров. На сетевой модели отражаются порядок и последовательность реализации проекта, сроки начала, окончания и продолжительности работ, резервы времени и др. Сетевая модель позволяет наглядно отобразить структуру комплекса работ и взаимосвязи между его элементами, эффективно влиять на ход реализации проекта. В этой сети работы изображаются дугами (стрелками), а в узлах сети помещаются события, обозначающие фиксированный момент окончания всех предшествующих работ и одновременного начала всех последующих работ. Модели подобного типа называют сетями, ориентированными на события. Характерной особенностью этого вида сетевых моделей является то, что длительности работ задаются детерминированными величинами (они записываются под стрелками соответствующих работ). Степень неопределенности проектной среды, в которой создан метод CPM, принимается достаточно малой, и исполнители могут довольно точно оценить длительность работ, основываясь на предыдущем опыте. Сетевая модель на основе метода СРМ 1 1 32 4 5 2 3 4 5 t 1 t 2 t 3 t 4 t 5 Событие Работа
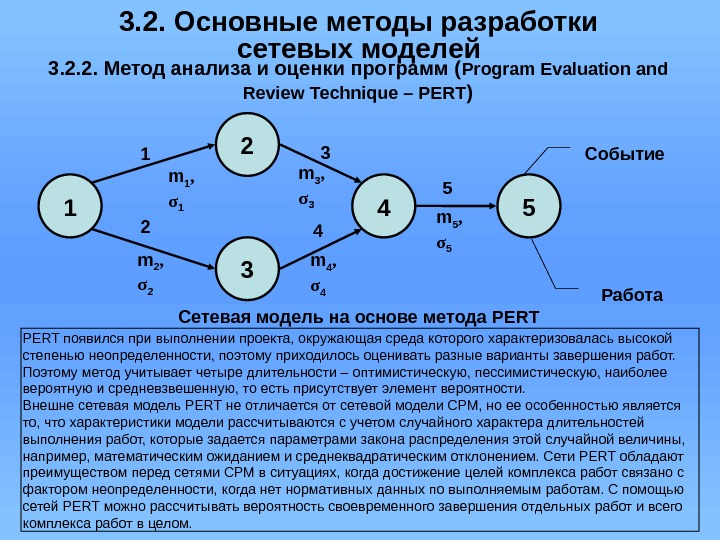
 3. 2. Основные методы разработки сетевых моделей 3. 2. 2. Метод анализа и оценки программ ( Program Evaluation and Review Technique – PERT ) m 1 , σ 1 m 3 , σ 3 m 2 , σ 2 m 4 , σ 4 m 5 , σ 5 Сетевая модель на основе метода PERT 1 1 32 4 5 2 3 4 5 Событие Работа PERT появился при выполнении проекта, окружающая среда которого характеризовалась высокой степенью неопределенности, поэтому приходилось оценивать разные варианты завершения работ. Поэтому метод учитывает четыре длительности – оптимистическую, пессимистическую, наиболее вероятную и средневзвешенную, то есть присутствует элемент вероятности. Внешне сетевая модель PERT не отличается от сетевой модели СРМ, но ее особенностью является то, что характеристики модели рассчитываются с учетом случайного характера длительностей выполнения работ, которые задается параметрами закона распределения этой случайной величины, например, математическим ожиданием и среднеквадратическим отклонением. Сети PERT обладают преимуществом перед сетями СРМ в ситуациях, когда достижение целей комплекса работ связано с фактором неопределенности, когда нет нормативных данных по выполняемым работам. С помощью сетей PERT можно рассчитывать вероятность своевременного завершения отдельных работ и всего комплекса работ в целом.
3. 2. Основные методы разработки сетевых моделей 3. 2. 2. Метод анализа и оценки программ ( Program Evaluation and Review Technique – PERT ) m 1 , σ 1 m 3 , σ 3 m 2 , σ 2 m 4 , σ 4 m 5 , σ 5 Сетевая модель на основе метода PERT 1 1 32 4 5 2 3 4 5 Событие Работа PERT появился при выполнении проекта, окружающая среда которого характеризовалась высокой степенью неопределенности, поэтому приходилось оценивать разные варианты завершения работ. Поэтому метод учитывает четыре длительности – оптимистическую, пессимистическую, наиболее вероятную и средневзвешенную, то есть присутствует элемент вероятности. Внешне сетевая модель PERT не отличается от сетевой модели СРМ, но ее особенностью является то, что характеристики модели рассчитываются с учетом случайного характера длительностей выполнения работ, которые задается параметрами закона распределения этой случайной величины, например, математическим ожиданием и среднеквадратическим отклонением. Сети PERT обладают преимуществом перед сетями СРМ в ситуациях, когда достижение целей комплекса работ связано с фактором неопределенности, когда нет нормативных данных по выполняемым работам. С помощью сетей PERT можно рассчитывать вероятность своевременного завершения отдельных работ и всего комплекса работ в целом.
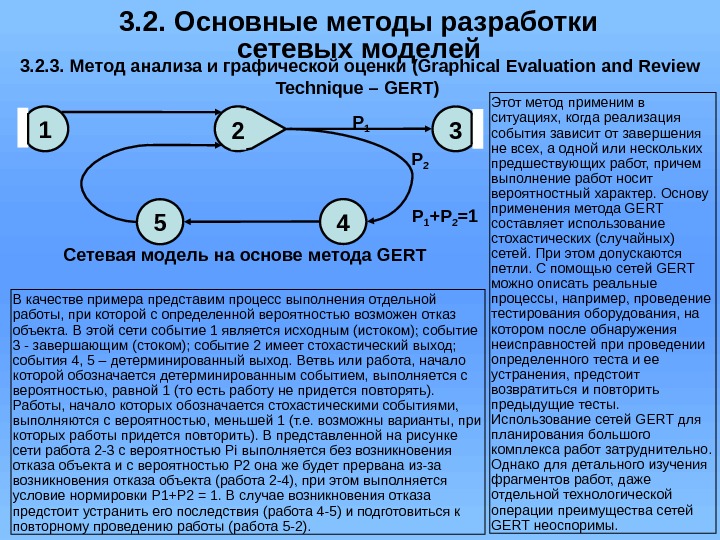
 3. 2. Основные методы разработки сетевых моделей 3. 2. 3. Метод анализа и графической оценки (Graphical Evaluation and Review Technique – GERT) Сетевая модель на основе метода GERT Р 1 Р 2 Р 1 +Р 2 =1 4 51 32 2 Этот метод применим в ситуациях, когда реализация события зависит от завершения не всех, а одной или нескольких предшествующих работ, причем выполнение работ носит вероятностный характер. Основу применения метода GERT составляет использование стохастических (случайных) сетей. При этом допускаются петли. С помощью сетей GERT можно описать реальные процессы, например, проведение тестирования оборудования, на котором после обнаружения неисправностей при проведении определенного теста и ее устранения, предстоит возвратиться и повторить предыдущие тесты. Использование сетей GERT для планирования большого комплекса работ затруднительно. Однако для детального изучения фрагментов работ, даже отдельной технологической операции преимущества сетей GERT неоспоримы. В качестве примера представим процесс выполнения отдельной работы, при которой с определенной вероятностью возможен отказ объекта. В этой сети событие 1 является исходным (истоком); событие 3 — завершающим (стоком); событие 2 имеет стохастический выход; события 4, 5 – детерминированный выход. Ветвь или работа, начало которой обозначается детерминированным событием, выполняется с вероятностью, равной 1 (то есть работу не придется повторять). Работы, начало которых обозначается стохастическими событиями, выполняются с вероятностью, меньшей 1 (т. е. возможны варианты, при которых работы придется повторить). В представленной на рисунке сети работа 2 -3 с вероятностью Pi выполняется без возникновения отказа объекта и с вероятностью Р 2 она же будет прервана из-за возникновения отказа объекта (работа 2 -4), при этом выполняется условие нормировки Р 1+Р 2 = 1. В случае возникновения отказа предстоит устранить его последствия (работа 4 -5) и подготовиться к повторному проведению работы (работа 5 -2).
3. 2. Основные методы разработки сетевых моделей 3. 2. 3. Метод анализа и графической оценки (Graphical Evaluation and Review Technique – GERT) Сетевая модель на основе метода GERT Р 1 Р 2 Р 1 +Р 2 =1 4 51 32 2 Этот метод применим в ситуациях, когда реализация события зависит от завершения не всех, а одной или нескольких предшествующих работ, причем выполнение работ носит вероятностный характер. Основу применения метода GERT составляет использование стохастических (случайных) сетей. При этом допускаются петли. С помощью сетей GERT можно описать реальные процессы, например, проведение тестирования оборудования, на котором после обнаружения неисправностей при проведении определенного теста и ее устранения, предстоит возвратиться и повторить предыдущие тесты. Использование сетей GERT для планирования большого комплекса работ затруднительно. Однако для детального изучения фрагментов работ, даже отдельной технологической операции преимущества сетей GERT неоспоримы. В качестве примера представим процесс выполнения отдельной работы, при которой с определенной вероятностью возможен отказ объекта. В этой сети событие 1 является исходным (истоком); событие 3 — завершающим (стоком); событие 2 имеет стохастический выход; события 4, 5 – детерминированный выход. Ветвь или работа, начало которой обозначается детерминированным событием, выполняется с вероятностью, равной 1 (то есть работу не придется повторять). Работы, начало которых обозначается стохастическими событиями, выполняются с вероятностью, меньшей 1 (т. е. возможны варианты, при которых работы придется повторить). В представленной на рисунке сети работа 2 -3 с вероятностью Pi выполняется без возникновения отказа объекта и с вероятностью Р 2 она же будет прервана из-за возникновения отказа объекта (работа 2 -4), при этом выполняется условие нормировки Р 1+Р 2 = 1. В случае возникновения отказа предстоит устранить его последствия (работа 4 -5) и подготовиться к повторному проведению работы (работа 5 -2).
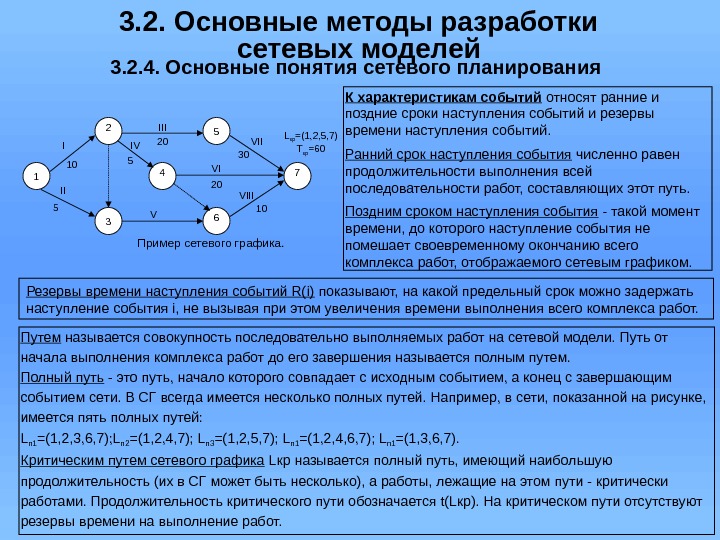
 3. 2. Основные методы разработки сетевых моделей 3. 2. 4. Основные понятия сетевого планирования Пример сетевого графика. 1 2 3 4 5 6 7 IVI II III V VI VIII L кр =(1, 2, 5, 7) T кр =60 10 5 5 20 20 30 10 Действительная работа – работа, для выполнения которой требуются затраты труда, времени и материальных ресурсов. На сетевом графике действительная работа изображается сплошной линией со стрелкой. Работа типа ожидание (ожиданием) – называется такая работа, которая не требует затрат труда и материальных ресурсов, но занимает некоторое время (например, проверка блока на вибростенде). На графике изображается также как действительная работа. Фиктивная работа – это не работа в привычном понимании этого слова, а логическая связь (зависимость), которая указывает на невозможность начала некоторых операций до окончания предшествующих работ. Фиктивная работа вводится для отражения правильной взаимосвязи между работами при построении СГ и изображается пунктирной линией без указания назначения и времени. К характеристикам работ относятся: полный резерв времени выполнения работы Rn(i, j) — показывает, на сколько можно увеличить продолжительность отдельной работы или отсрочить ее начало, не изменяя при этом заданного срока окончания всего комплекса работ; свободный резерв времени выполнения работы Rсв(i, j) — показывает, на сколько можно увеличить продолжительность отдельной работы или отсрочить ее начало, не изменяя ранних сроков начала последующих работ, при условии, что начальное событие этой работы наступило в свой ранний срок. независимый резерв времени работы появляется, если полный резерв предшествующей работы меньше свободного резерва данной работы, и может быть использован на данной работе независимо ни от предыдущих, ни от последующих работ. Событие сетевого графика – представляет собой логический элемент, который означает факт (возможность) начала или завершения одной или нескольких работ и соответствует получению конкретного результата в изображаемом сетевым графиком процессе. Чаще всего обозначается кружком. Совершение события означает, что открыт фронт для последующих работ (например, сборка изделия закончена, можно переходить к тестированию). Если событие является результатом нескольких работ , то оно считается свершившимся после выполнения всех этих работ. Факт свершения события является непременным условием для начала выполнения выходящих из него работ.
3. 2. Основные методы разработки сетевых моделей 3. 2. 4. Основные понятия сетевого планирования Пример сетевого графика. 1 2 3 4 5 6 7 IVI II III V VI VIII L кр =(1, 2, 5, 7) T кр =60 10 5 5 20 20 30 10 Действительная работа – работа, для выполнения которой требуются затраты труда, времени и материальных ресурсов. На сетевом графике действительная работа изображается сплошной линией со стрелкой. Работа типа ожидание (ожиданием) – называется такая работа, которая не требует затрат труда и материальных ресурсов, но занимает некоторое время (например, проверка блока на вибростенде). На графике изображается также как действительная работа. Фиктивная работа – это не работа в привычном понимании этого слова, а логическая связь (зависимость), которая указывает на невозможность начала некоторых операций до окончания предшествующих работ. Фиктивная работа вводится для отражения правильной взаимосвязи между работами при построении СГ и изображается пунктирной линией без указания назначения и времени. К характеристикам работ относятся: полный резерв времени выполнения работы Rn(i, j) — показывает, на сколько можно увеличить продолжительность отдельной работы или отсрочить ее начало, не изменяя при этом заданного срока окончания всего комплекса работ; свободный резерв времени выполнения работы Rсв(i, j) — показывает, на сколько можно увеличить продолжительность отдельной работы или отсрочить ее начало, не изменяя ранних сроков начала последующих работ, при условии, что начальное событие этой работы наступило в свой ранний срок. независимый резерв времени работы появляется, если полный резерв предшествующей работы меньше свободного резерва данной работы, и может быть использован на данной работе независимо ни от предыдущих, ни от последующих работ. Событие сетевого графика – представляет собой логический элемент, который означает факт (возможность) начала или завершения одной или нескольких работ и соответствует получению конкретного результата в изображаемом сетевым графиком процессе. Чаще всего обозначается кружком. Совершение события означает, что открыт фронт для последующих работ (например, сборка изделия закончена, можно переходить к тестированию). Если событие является результатом нескольких работ , то оно считается свершившимся после выполнения всех этих работ. Факт свершения события является непременным условием для начала выполнения выходящих из него работ.
 Путем называется совокупность последовательно выполняемых работ на сетевой модели. Путь от начала выполнения комплекса работ до его завершения называется полным путем. Полный путь — это путь, начало которого совпадает с исходным событием, а конец с завершающим событием сети. В СГ всегда имеется несколько полных путей. Например, в сети, показанной на рисунке, имеется пять полных путей: L п 1 =(1, 2, 3, 6, 7); L п 2 =(1, 2, 4, 7); L п 3 =(1, 2, 5, 7); L п 1 =(1, 2, 4, 6, 7); L п 1 =(1, 3, 6, 7). Критическим путем сетевого графика Lкр называется полный путь, имеющий наибольшую продолжительность (их в СГ может быть несколько), а работы, лежащие на этом пути — критически работами. Продолжительность критического пути обозначается t(Lкр). На критическом пути отсутствуют резервы времени на выполнение работ. 3. 2. Основные методы разработки сетевых моделей 3. 2. 4. Основные понятия сетевого планирования К характеристикам событий относят ранние и поздние сроки наступления событий и резервы времени наступления событий. Ранний срок наступления события численно равен продолжительности выполнения всей последовательности работ, составляющих этот путь. Поздним сроком наступления события — такой момент времени, до которого наступление события не помешает своевременному окончанию всего комплекса работ, отображаемого сетевым графиком. Пример сетевого графика. 1 2 3 4 5 6 7 IVI II III V VI VIII L кр =(1, 2, 5, 7) T кр =60 10 5 5 20 20 30 10 Резервы времени наступления событий R(i) показывают, на какой предельный срок можно задержать наступление события i, не вызывая при этом увеличения времени выполнения всего комплекса работ.
Путем называется совокупность последовательно выполняемых работ на сетевой модели. Путь от начала выполнения комплекса работ до его завершения называется полным путем. Полный путь — это путь, начало которого совпадает с исходным событием, а конец с завершающим событием сети. В СГ всегда имеется несколько полных путей. Например, в сети, показанной на рисунке, имеется пять полных путей: L п 1 =(1, 2, 3, 6, 7); L п 2 =(1, 2, 4, 7); L п 3 =(1, 2, 5, 7); L п 1 =(1, 2, 4, 6, 7); L п 1 =(1, 3, 6, 7). Критическим путем сетевого графика Lкр называется полный путь, имеющий наибольшую продолжительность (их в СГ может быть несколько), а работы, лежащие на этом пути — критически работами. Продолжительность критического пути обозначается t(Lкр). На критическом пути отсутствуют резервы времени на выполнение работ. 3. 2. Основные методы разработки сетевых моделей 3. 2. 4. Основные понятия сетевого планирования К характеристикам событий относят ранние и поздние сроки наступления событий и резервы времени наступления событий. Ранний срок наступления события численно равен продолжительности выполнения всей последовательности работ, составляющих этот путь. Поздним сроком наступления события — такой момент времени, до которого наступление события не помешает своевременному окончанию всего комплекса работ, отображаемого сетевым графиком. Пример сетевого графика. 1 2 3 4 5 6 7 IVI II III V VI VIII L кр =(1, 2, 5, 7) T кр =60 10 5 5 20 20 30 10 Резервы времени наступления событий R(i) показывают, на какой предельный срок можно задержать наступление события i, не вызывая при этом увеличения времени выполнения всего комплекса работ.
 3. 3. Методика построения сетевой модели 3. 3. 1. Подготовка исходных данных В ходе построения и расчета СГ целесообразно придерживаться следующего порядка работы: • составить таблицу исходных данных, содержащую перечень всех работ (этапов) проекта, последовательность и продолжительность их выполнения; • построить сетевую модель проекта; • провести упорядочение нумерации событий СГ; • провести расчет параметров сетевого графика и его, анализ, на основании которого определить, насколько рационально доставлен СГ, какие работы (этапы) в случае их невыполнения в срок могут привести к срыву всего комплекса работ, основные пути улучшения СГ проекта. 1. Составление таблицы исходных данных Начальная информация о планируемом проекте сосредоточена в техническом задании. Анализ разделов задания, в которых содержится перечень всех мероприятий, выполняемых в процессе реализации проекта, последовательность их выполнения и продолжительность каждого из них, позволяет определить, что является исходным и завершающим событием проекта, какова его конечная цель; выявить объем промежуточных работ, ведущих к завершающему событию, их взаимосвязь и возможность параллельного выполнения. Такой порядок возможен при наличии проектов-аналогов. Однако чаще бывает необходимо уже на этом этапе самостоятельно определять этапы проекта. В этом случае целесообразно выбирать модель, основанную на методе PERT, т. к. в проекте будет присутствовать вероятностная составляющая как по составу этапов и мероприятий, так и по их длительности. Полученную в ходе анализа исходную информацию удобно представить в виде таблицы. В таблицу так же целесообразно свести и информацию по ресурсам, затратам и т. п. для каждого из этапов.
3. 3. Методика построения сетевой модели 3. 3. 1. Подготовка исходных данных В ходе построения и расчета СГ целесообразно придерживаться следующего порядка работы: • составить таблицу исходных данных, содержащую перечень всех работ (этапов) проекта, последовательность и продолжительность их выполнения; • построить сетевую модель проекта; • провести упорядочение нумерации событий СГ; • провести расчет параметров сетевого графика и его, анализ, на основании которого определить, насколько рационально доставлен СГ, какие работы (этапы) в случае их невыполнения в срок могут привести к срыву всего комплекса работ, основные пути улучшения СГ проекта. 1. Составление таблицы исходных данных Начальная информация о планируемом проекте сосредоточена в техническом задании. Анализ разделов задания, в которых содержится перечень всех мероприятий, выполняемых в процессе реализации проекта, последовательность их выполнения и продолжительность каждого из них, позволяет определить, что является исходным и завершающим событием проекта, какова его конечная цель; выявить объем промежуточных работ, ведущих к завершающему событию, их взаимосвязь и возможность параллельного выполнения. Такой порядок возможен при наличии проектов-аналогов. Однако чаще бывает необходимо уже на этом этапе самостоятельно определять этапы проекта. В этом случае целесообразно выбирать модель, основанную на методе PERT, т. к. в проекте будет присутствовать вероятностная составляющая как по составу этапов и мероприятий, так и по их длительности. Полученную в ходе анализа исходную информацию удобно представить в виде таблицы. В таблицу так же целесообразно свести и информацию по ресурсам, затратам и т. п. для каждого из этапов.
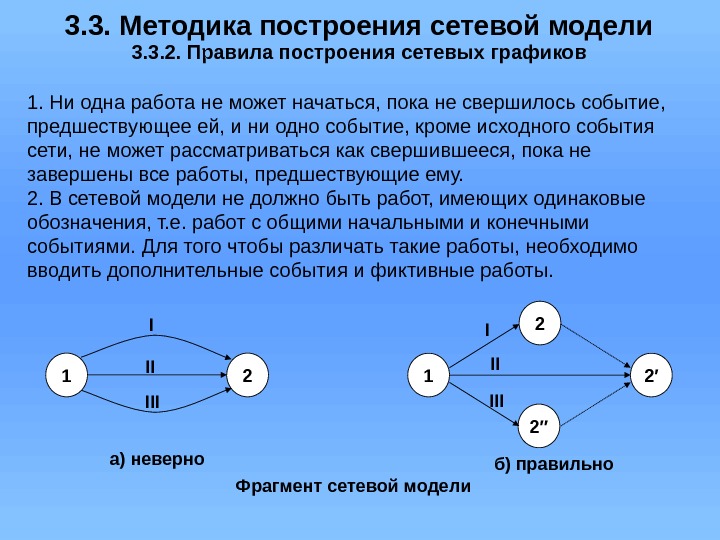
 3. 3. Методика построения сетевой модели 3. 3. 2. Правила построения сетевых графиков 1. Ни одна работа не может начаться, пока не свершилось событие, предшествующее ей, и ни одно событие, кроме исходного события сети, не может рассматриваться как свершившееся, пока не завершены все работы, предшествующие ему. 2. В сетевой модели не должно быть работ, имеющих одинаковые обозначения, т. е. работ с общими начальными и конечными событиями. Для того чтобы различать такие работы, необходимо вводить дополнительные события и фиктивные работы. 1 2 а) неверно II I III 1 2′ б) правильно. III 2″ 2 Фрагмент сетевой модели
3. 3. Методика построения сетевой модели 3. 3. 2. Правила построения сетевых графиков 1. Ни одна работа не может начаться, пока не свершилось событие, предшествующее ей, и ни одно событие, кроме исходного события сети, не может рассматриваться как свершившееся, пока не завершены все работы, предшествующие ему. 2. В сетевой модели не должно быть работ, имеющих одинаковые обозначения, т. е. работ с общими начальными и конечными событиями. Для того чтобы различать такие работы, необходимо вводить дополнительные события и фиктивные работы. 1 2 а) неверно II I III 1 2′ б) правильно. III 2″ 2 Фрагмент сетевой модели
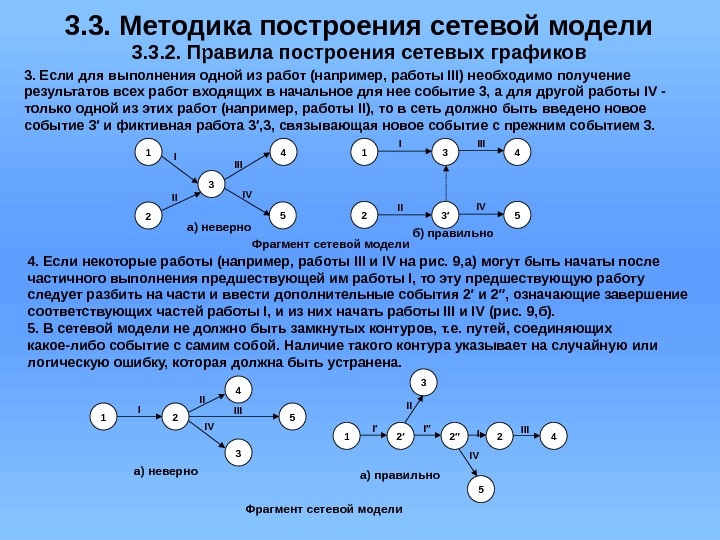
 3. 3. Методика построения сетевой модели 3. 3. 2. Правила построения сетевых графиков 3. Если для выполнения одной из работ (например, работы III) необходимо получение результатов всех работ входящих в начальное для нее событие 3, а для другой работы IV — только одной из этих работ (например, работы II), то в сеть должно быть введено новое событие 3′ и фиктивная работа 3′, 3, связывающая новое событие с прежним событием 3. 3 2 а) неверно. II I III 5 41 IV 1 2 3 3′ 4 5 I II IV б) правильно Фрагмент сетевой модели 4. Если некоторые работы (например, работы III и IV на рис. 9, а) могут быть начаты после частичного выполнения предшествующей им работы I, то эту предшествующую работу следует разбить на части и ввести дополнительные события 2′ и 2″, означающие завершение соответствующих частей работы I, и из них начать работы III и IV (рис. 9, б). 5. В сетевой модели не должно быть замкнутых контуров, т. е. путей, соединяющих какое-либо событие с самим собой. Наличие такого контура указывает на случайную или логическую ошибку, которая должна быть устранена. 1 I 2 34 5 II III а) неверно IV 1 I′ 2′ 3 4 5 II III а) правильно IV 2′′ 2 I′′ I Фрагмент сетевой модели
3. 3. Методика построения сетевой модели 3. 3. 2. Правила построения сетевых графиков 3. Если для выполнения одной из работ (например, работы III) необходимо получение результатов всех работ входящих в начальное для нее событие 3, а для другой работы IV — только одной из этих работ (например, работы II), то в сеть должно быть введено новое событие 3′ и фиктивная работа 3′, 3, связывающая новое событие с прежним событием 3. 3 2 а) неверно. II I III 5 41 IV 1 2 3 3′ 4 5 I II IV б) правильно Фрагмент сетевой модели 4. Если некоторые работы (например, работы III и IV на рис. 9, а) могут быть начаты после частичного выполнения предшествующей им работы I, то эту предшествующую работу следует разбить на части и ввести дополнительные события 2′ и 2″, означающие завершение соответствующих частей работы I, и из них начать работы III и IV (рис. 9, б). 5. В сетевой модели не должно быть замкнутых контуров, т. е. путей, соединяющих какое-либо событие с самим собой. Наличие такого контура указывает на случайную или логическую ошибку, которая должна быть устранена. 1 I 2 34 5 II III а) неверно IV 1 I′ 2′ 3 4 5 II III а) правильно IV 2′′ 2 I′′ I Фрагмент сетевой модели
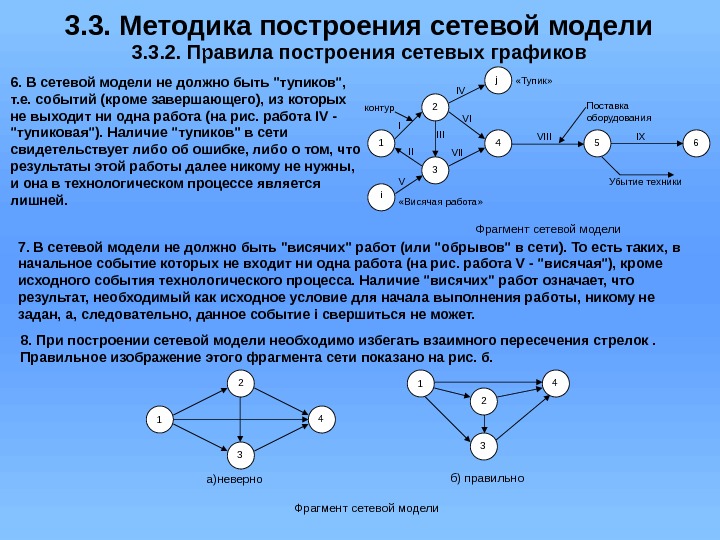
 3. 3. Методика построения сетевой модели 3. 3. 2. Правила построения сетевых графиков 6. В сетевой модели не должно быть «тупиков», т. е. событий (кроме завершающего), из которых не выходит ни одна работа (на рис. работа IV — «тупиковая»). Наличие «тупиков» в сети свидетельствует либо об ошибке, либо о том, что результаты этой работы далее никому не нужны, и она в технологическом процессе является лишней. I 1 i 2 3 4 5 j 6 IXIII II IV V VII VI VIIIконтур «Тупик» «Висячая работа» Поставка оборудования Убытие техники Фрагмент сетевой модели 8. При построении сетевой модели необходимо избегать взаимного пересечения стрелок. Правильное изображение этого фрагмента сети показано на рис. б. 7. В сетевой модели не должно быть «висячих» работ (или «обрывов» в сети). То есть таких, в начальное событие которых не входит ни одна работа (на рис. работа V — «висячая»), кроме исходного события технологического процесса. Наличие «висячих» работ означает, что результат, необходимый как исходное условие для начала выполнения работы, никому не задан, а, следовательно, данное событие i свершиться не может. б) правильно 1 2 3 4 а)неверно 1 4 2 3 Фрагмент сетевой модели
3. 3. Методика построения сетевой модели 3. 3. 2. Правила построения сетевых графиков 6. В сетевой модели не должно быть «тупиков», т. е. событий (кроме завершающего), из которых не выходит ни одна работа (на рис. работа IV — «тупиковая»). Наличие «тупиков» в сети свидетельствует либо об ошибке, либо о том, что результаты этой работы далее никому не нужны, и она в технологическом процессе является лишней. I 1 i 2 3 4 5 j 6 IXIII II IV V VII VI VIIIконтур «Тупик» «Висячая работа» Поставка оборудования Убытие техники Фрагмент сетевой модели 8. При построении сетевой модели необходимо избегать взаимного пересечения стрелок. Правильное изображение этого фрагмента сети показано на рис. б. 7. В сетевой модели не должно быть «висячих» работ (или «обрывов» в сети). То есть таких, в начальное событие которых не входит ни одна работа (на рис. работа V — «висячая»), кроме исходного события технологического процесса. Наличие «висячих» работ означает, что результат, необходимый как исходное условие для начала выполнения работы, никому не задан, а, следовательно, данное событие i свершиться не может. б) правильно 1 2 3 4 а)неверно 1 4 2 3 Фрагмент сетевой модели
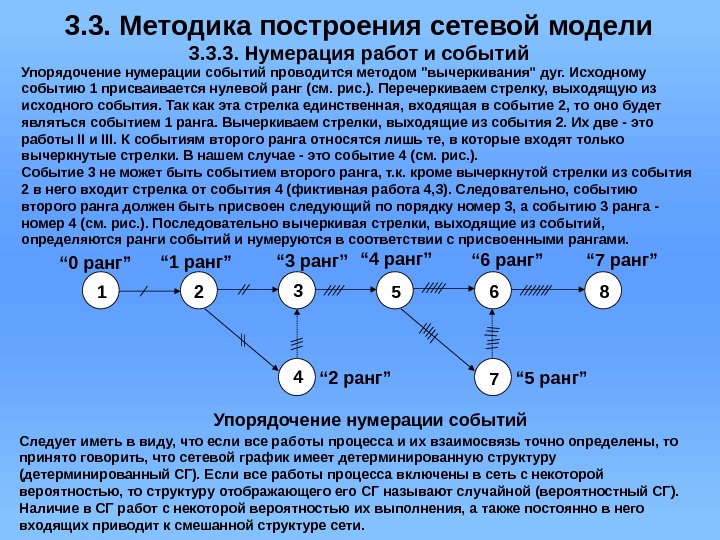
 3. 3. Методика построения сетевой модели 3. 3. 3. Нумерация работ и событий Упорядочение нумерации событий проводится методом «вычеркивания» дуг. Исходному событию 1 присваивается нулевой ранг (см. рис. ). Перечеркиваем стрелку, выходящую из исходного события. Так как эта стрелка единственная, входящая в событие 2, то оно будет являться событием 1 ранга. Вычеркиваем стрелки, выходящие из события 2. Их две — это работы II и III. К событиям второго ранга относятся лишь те, в которые входят только вычеркнутые стрелки. В нашем случае — это событие 4 (см. рис. ). Событие 3 не может быть событием второго ранга, т. к. кроме вычеркнутой стрелки из события 2 в него входит стрелка от события 4 (фиктивная работа 4, 3). Следовательно, событию второго ранга должен быть присвоен следующий по порядку номер 3, а событию 3 ранга — номер 4 (см. рис. ). Последовательно вычеркивая стрелки, выходящие из событий, определяются ранги событий и нумеруются в соответствии с присвоенными рангами. “ 0 ранг” 51 2 3 4 6 8 Упорядочение нумерации событий 7“ 1 ранг” “ 2 ранг”“ 3 ранг” “ 4 ранг” “ 5 ранг”“ 6 ранг” “ 7 ранг” Следует иметь в виду, что если все работы процесса и их взаимосвязь точно определены, то принято говорить, что сетевой график имеет детерминированную структуру (детерминированный СГ). Если все работы процесса включены в сеть с некоторой вероятностью, то структуру отображающего СГ называют случайной (вероятностный СГ). Наличие в СГ работ с некоторой вероятностью их выполнения, а также постоянно в него входящих приводит к смешанной структуре сети.
3. 3. Методика построения сетевой модели 3. 3. 3. Нумерация работ и событий Упорядочение нумерации событий проводится методом «вычеркивания» дуг. Исходному событию 1 присваивается нулевой ранг (см. рис. ). Перечеркиваем стрелку, выходящую из исходного события. Так как эта стрелка единственная, входящая в событие 2, то оно будет являться событием 1 ранга. Вычеркиваем стрелки, выходящие из события 2. Их две — это работы II и III. К событиям второго ранга относятся лишь те, в которые входят только вычеркнутые стрелки. В нашем случае — это событие 4 (см. рис. ). Событие 3 не может быть событием второго ранга, т. к. кроме вычеркнутой стрелки из события 2 в него входит стрелка от события 4 (фиктивная работа 4, 3). Следовательно, событию второго ранга должен быть присвоен следующий по порядку номер 3, а событию 3 ранга — номер 4 (см. рис. ). Последовательно вычеркивая стрелки, выходящие из событий, определяются ранги событий и нумеруются в соответствии с присвоенными рангами. “ 0 ранг” 51 2 3 4 6 8 Упорядочение нумерации событий 7“ 1 ранг” “ 2 ранг”“ 3 ранг” “ 4 ранг” “ 5 ранг”“ 6 ранг” “ 7 ранг” Следует иметь в виду, что если все работы процесса и их взаимосвязь точно определены, то принято говорить, что сетевой график имеет детерминированную структуру (детерминированный СГ). Если все работы процесса включены в сеть с некоторой вероятностью, то структуру отображающего СГ называют случайной (вероятностный СГ). Наличие в СГ работ с некоторой вероятностью их выполнения, а также постоянно в него входящих приводит к смешанной структуре сети.
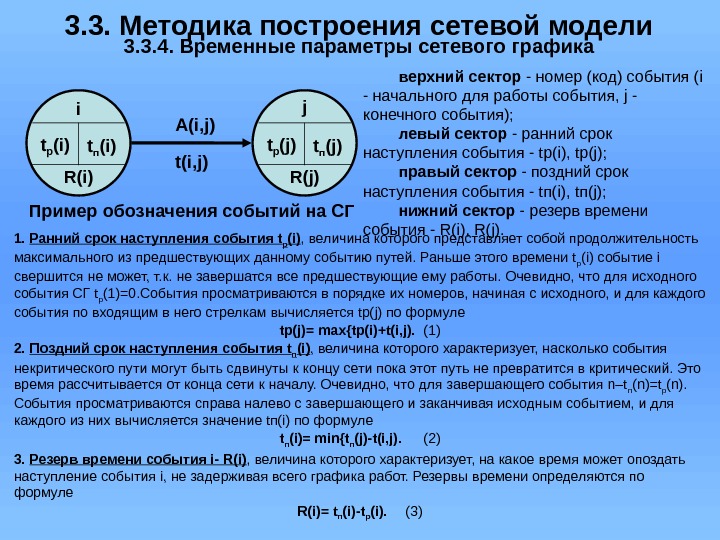
 3. 3. Методика построения сетевой модели 3. 3. 4. Временные параметры сетевого графика А(i, j)i t р (i) t п (i) R(i) t(i, j) Пример обозначения событий на СГ j t р (j) t п (j) R(j) верхний сектор — номер (код) события (i — начального для работы события, j — конечного события); левый сектор — ранний срок наступления события — tр(i), tр(j); правый сектор — поздний срок наступления события — tп(i), tп(j); нижний сектор — резерв времени события — R(i), R(j). 1. Ранний срок наступления события t р (i) , величина которого представляет собой продолжительность максимального из предшествующих данному событию путей. Раньше этого времени t р (i) событие i свершится не может, т. к. не завершатся все предшествующие ему работы. Очевидно, что для исходного события СГ t р (1)=0. События просматриваются в порядке их номеров, начиная с исходного, и для каждого события по входящим в него стрелкам вычисляется tр(j) по формуле tр(j)= max{tр(i)+t(i, j). (1) 2. Поздний срок наступления события t п (i) , величина которого характеризует, насколько события некритического пути могут быть сдвинуты к концу сети пока этот путь не превратится в критический. Это время рассчитывается от конца сети к началу. Очевидно, что для завершающего события n–t п (n)=t р (n). События просматриваются справа налево с завершающего и заканчивая исходным событием, и для каждого из них вычисляется значение tп(i) по формуле t п (i)= min{t п (j)-t(i, j). (2) 3. Резерв времени события i- R(i) , величина которого характеризует, на какое время может опоздать наступление события i, не задерживая всего графика работ. Резервы времени определяются по формуле R(i)= t п (i)-t р (i). (3)
3. 3. Методика построения сетевой модели 3. 3. 4. Временные параметры сетевого графика А(i, j)i t р (i) t п (i) R(i) t(i, j) Пример обозначения событий на СГ j t р (j) t п (j) R(j) верхний сектор — номер (код) события (i — начального для работы события, j — конечного события); левый сектор — ранний срок наступления события — tр(i), tр(j); правый сектор — поздний срок наступления события — tп(i), tп(j); нижний сектор — резерв времени события — R(i), R(j). 1. Ранний срок наступления события t р (i) , величина которого представляет собой продолжительность максимального из предшествующих данному событию путей. Раньше этого времени t р (i) событие i свершится не может, т. к. не завершатся все предшествующие ему работы. Очевидно, что для исходного события СГ t р (1)=0. События просматриваются в порядке их номеров, начиная с исходного, и для каждого события по входящим в него стрелкам вычисляется tр(j) по формуле tр(j)= max{tр(i)+t(i, j). (1) 2. Поздний срок наступления события t п (i) , величина которого характеризует, насколько события некритического пути могут быть сдвинуты к концу сети пока этот путь не превратится в критический. Это время рассчитывается от конца сети к началу. Очевидно, что для завершающего события n–t п (n)=t р (n). События просматриваются справа налево с завершающего и заканчивая исходным событием, и для каждого из них вычисляется значение tп(i) по формуле t п (i)= min{t п (j)-t(i, j). (2) 3. Резерв времени события i- R(i) , величина которого характеризует, на какое время может опоздать наступление события i, не задерживая всего графика работ. Резервы времени определяются по формуле R(i)= t п (i)-t р (i). (3)
 3. 3. Методика построения сетевой модели 3. 3. 4. Временные параметры сетевого графика А(i, j)i t р (i) t п (i) R(i) t(i, j) Пример обозначения событий на СГ j t р (j) t п (j) R(j) верхний сектор — номер (код) события (i — начального для работы события, j — конечного события); левый сектор — ранний срок наступления события — tр(i), tр(j); правый сектор — поздний срок наступления события — tп(i), tп(j); нижний сектор — резерв времени события — R(i), R(j). Расчет параметров работ проводится с использованием полученных значений параметров событий. К параметрам работ относятся: ранний срок начала работы – t рн (i, j)= t р (i); (4) поздний срок окончания работы – t по (i, j)= t п (j); (5) ранний срок окончания работы – t ро (i, j)= t р (i)+t(i, j); (6) поздний срок начала работы – t пн (i, j)= t п (j)-t(i, j); (7) полный резерв времени работы – R п (i, j)= t п (j)-t р (i)-t(i, j); (8) свободный резерв времени работы – R с (i, j)= t р (j)-t р (i)-t(i, j). (9) независимый резерв времени работы – R н (i, j)=t р (j)-t п (i)-t(i, j). (10) Для контроля правильности расчетов следует иметь в виду следующее соотношение: Rн(i, j)≤ Rс(i, j)≤ Rп(i, j). (11) Он появляется, если полный резерв предшествующей работы меньше свободного резерва данной работы, и может быть использован на данной работе независимо ни от предыдущих, ни от последующих работ.
3. 3. Методика построения сетевой модели 3. 3. 4. Временные параметры сетевого графика А(i, j)i t р (i) t п (i) R(i) t(i, j) Пример обозначения событий на СГ j t р (j) t п (j) R(j) верхний сектор — номер (код) события (i — начального для работы события, j — конечного события); левый сектор — ранний срок наступления события — tр(i), tр(j); правый сектор — поздний срок наступления события — tп(i), tп(j); нижний сектор — резерв времени события — R(i), R(j). Расчет параметров работ проводится с использованием полученных значений параметров событий. К параметрам работ относятся: ранний срок начала работы – t рн (i, j)= t р (i); (4) поздний срок окончания работы – t по (i, j)= t п (j); (5) ранний срок окончания работы – t ро (i, j)= t р (i)+t(i, j); (6) поздний срок начала работы – t пн (i, j)= t п (j)-t(i, j); (7) полный резерв времени работы – R п (i, j)= t п (j)-t р (i)-t(i, j); (8) свободный резерв времени работы – R с (i, j)= t р (j)-t р (i)-t(i, j). (9) независимый резерв времени работы – R н (i, j)=t р (j)-t п (i)-t(i, j). (10) Для контроля правильности расчетов следует иметь в виду следующее соотношение: Rн(i, j)≤ Rс(i, j)≤ Rп(i, j). (11) Он появляется, если полный резерв предшествующей работы меньше свободного резерва данной работы, и может быть использован на данной работе независимо ни от предыдущих, ни от последующих работ.
 3. 3. Методика построения сетевой модели 3. 3. 5. Анализ сетевого графика Анализ СГ проводится с целью определения, насколько рационально составлен сетевой график технологического процесса, какие работы в случае их невыполнения в срок могут привести к срыву всего комплекса работ, а также наметить основные пути улучшения сетевого графика для сокращения сроков реализации процесса в целом. (12)Отыскание критического пути СГ. Необходимый признак наличия критического пути — R(i)=0. Необходимый и достаточный признак наличия критического пути – R п (i, j)=0. Степень критичности пути L i можно оценить с помощью коэффициента напряженности пути, рассчитываемого по формуле Оценка напряженности отдельных работ. Степень сложности выполнения каждой работы некритического пути можно охарактеризовать с помощью коэффициента напряженности работы. Коэффициент напряженности работы – это отношение продолжительности несовпадающих – заключенных между одними и теми же событиями – отрезков пути, одним из которых является путь максимальной продолжительности, проходящий через данную работу, а другим критический путь (13) где t’(L кр ) – величина отрезка пути, совпадающая с критическим путем. В зависимости от значения коэффициента работы распределяются по зонам – критическая (кэф-т равен 1), подкритическая и резервная (коэф-т меньше единицы). Для удобства анализа результаты расчетов сводятся в таблицыю. )t(L )(LK ii iн , )(Lt’)t(L j)(i, R 1 j)(i, K кркр n н
3. 3. Методика построения сетевой модели 3. 3. 5. Анализ сетевого графика Анализ СГ проводится с целью определения, насколько рационально составлен сетевой график технологического процесса, какие работы в случае их невыполнения в срок могут привести к срыву всего комплекса работ, а также наметить основные пути улучшения сетевого графика для сокращения сроков реализации процесса в целом. (12)Отыскание критического пути СГ. Необходимый признак наличия критического пути — R(i)=0. Необходимый и достаточный признак наличия критического пути – R п (i, j)=0. Степень критичности пути L i можно оценить с помощью коэффициента напряженности пути, рассчитываемого по формуле Оценка напряженности отдельных работ. Степень сложности выполнения каждой работы некритического пути можно охарактеризовать с помощью коэффициента напряженности работы. Коэффициент напряженности работы – это отношение продолжительности несовпадающих – заключенных между одними и теми же событиями – отрезков пути, одним из которых является путь максимальной продолжительности, проходящий через данную работу, а другим критический путь (13) где t’(L кр ) – величина отрезка пути, совпадающая с критическим путем. В зависимости от значения коэффициента работы распределяются по зонам – критическая (кэф-т равен 1), подкритическая и резервная (коэф-т меньше единицы). Для удобства анализа результаты расчетов сводятся в таблицыю. )t(L )(LK ii iн , )(Lt’)t(L j)(i, R 1 j)(i, K кркр n н
 3. 3. Методика построения сетевой модели 3. 3. 5. Анализ сетевого графика В ходе анализа временных параметров событий и работ СГ прежде всего необходимо определить те работы на критическом пути, сокращение которых дает наибольший эффект. Нужно оценить характер этих работ, их составляющие (компоненты), определяющие их продолжительность (например) : • время, затрачиваемое на ручные операции; • машинное время; • время и содержание развертывания тестовой аппаратуры; • содержание операций тестирования; • время и содержание операций по приведение аппаратуры и т. д. Сокращение времени выполнения этих работ может быть достигнуто за счет: • повышения мастерства персонала; • за счет механизации ручных операций; • привлечением дополнительного персонала; • перепланирование работ для их параллельного выполнения (если это позволяет технология работ и наличие ресурсов); • улучшения организации проведения работ. При этом необходимо учитывать, что изменение продолжительности некоторых видов работ критического пути, может привести к образованию нового критического пути. Таким образом, сетевой график по содержанию – это логическое «проигрывание» всех работ в их диалектической взаимосвязи, обусловленности, последовательности. По форме он представляет собой графическое отражение на бумаге при помощи условных обозначений всех процессов во времени и последовательности их исполнения.
3. 3. Методика построения сетевой модели 3. 3. 5. Анализ сетевого графика В ходе анализа временных параметров событий и работ СГ прежде всего необходимо определить те работы на критическом пути, сокращение которых дает наибольший эффект. Нужно оценить характер этих работ, их составляющие (компоненты), определяющие их продолжительность (например) : • время, затрачиваемое на ручные операции; • машинное время; • время и содержание развертывания тестовой аппаратуры; • содержание операций тестирования; • время и содержание операций по приведение аппаратуры и т. д. Сокращение времени выполнения этих работ может быть достигнуто за счет: • повышения мастерства персонала; • за счет механизации ручных операций; • привлечением дополнительного персонала; • перепланирование работ для их параллельного выполнения (если это позволяет технология работ и наличие ресурсов); • улучшения организации проведения работ. При этом необходимо учитывать, что изменение продолжительности некоторых видов работ критического пути, может привести к образованию нового критического пути. Таким образом, сетевой график по содержанию – это логическое «проигрывание» всех работ в их диалектической взаимосвязи, обусловленности, последовательности. По форме он представляет собой графическое отражение на бумаге при помощи условных обозначений всех процессов во времени и последовательности их исполнения.
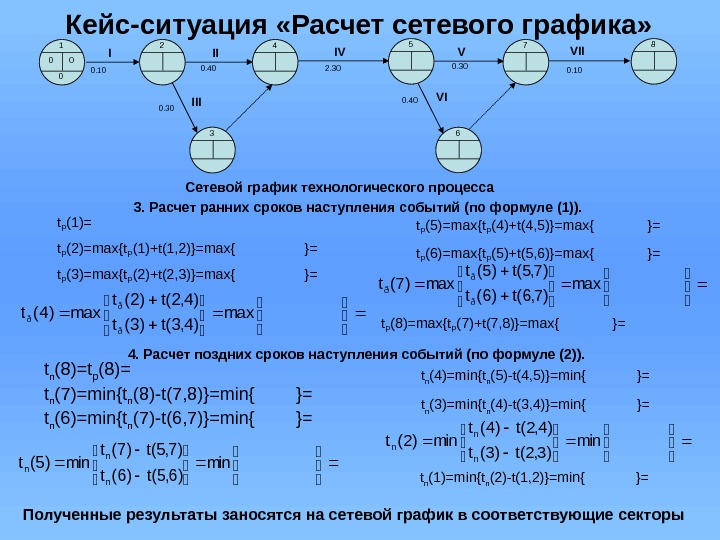
 Кейс-ситуация «Расчет сетевого графика» 1. Составление таблицы исходных данных Код работы Наименование работы Какой работе предшествует Затраты Кто выполняет Продолжительность работ, ч. , мин. I Подача тестируемой аппаратуры со склада II, III Эл. энергия, з/п Зав. складом, складских рабочих Зав. складом, рабочие склада – 2 человека 0 ч. 10 мин. II Подготовка стенда и аппаратуры к тестированию IV Эл. энергия, з/п лаборанта, специалиста по тестированию Лаборант, специалист по тестированию 0 ч. 40 мин. III Сборка схемы для проведения тестирования V З/п специалиста по тестированию Специалист по тестированию 0 ч. 30 мин. IV Тестирование образца V, VI Эл. энергия, з/п представителя ОТК, специалиста по тестированию Специалист по тестированию, представитель ОТК 2 ч. 30 мин. V Свертывание аппаратуры VII З/п специалиста по тестированию Специалист по тестированию 0 ч. 30 мин. VI Приведение аппаратуры в исходное положение VII Эл. энергия, з/п лаборанта, специалиста по тестированию Лаборант, специалист по тестированию 0 ч. 40 мин. VII Передача аппаратуры на склад для отгрузки потребителю — Эл. энергия, з/п Начальника склада, складских рабочих Начальник склада, складские рабочие 0 ч. 10 мин. Таблица 1 00 1 0 2 4 5 7 8 3 6 Сетевой график технологического процесса 0. 300. 10 0. 40 2. 30 0. 40 0. 102. Построение сетевой модели I II V VIIV III
Кейс-ситуация «Расчет сетевого графика» 1. Составление таблицы исходных данных Код работы Наименование работы Какой работе предшествует Затраты Кто выполняет Продолжительность работ, ч. , мин. I Подача тестируемой аппаратуры со склада II, III Эл. энергия, з/п Зав. складом, складских рабочих Зав. складом, рабочие склада – 2 человека 0 ч. 10 мин. II Подготовка стенда и аппаратуры к тестированию IV Эл. энергия, з/п лаборанта, специалиста по тестированию Лаборант, специалист по тестированию 0 ч. 40 мин. III Сборка схемы для проведения тестирования V З/п специалиста по тестированию Специалист по тестированию 0 ч. 30 мин. IV Тестирование образца V, VI Эл. энергия, з/п представителя ОТК, специалиста по тестированию Специалист по тестированию, представитель ОТК 2 ч. 30 мин. V Свертывание аппаратуры VII З/п специалиста по тестированию Специалист по тестированию 0 ч. 30 мин. VI Приведение аппаратуры в исходное положение VII Эл. энергия, з/п лаборанта, специалиста по тестированию Лаборант, специалист по тестированию 0 ч. 40 мин. VII Передача аппаратуры на склад для отгрузки потребителю — Эл. энергия, з/п Начальника склада, складских рабочих Начальник склада, складские рабочие 0 ч. 10 мин. Таблица 1 00 1 0 2 4 5 7 8 3 6 Сетевой график технологического процесса 0. 300. 10 0. 40 2. 30 0. 40 0. 102. Построение сетевой модели I II V VIIV III
 Кейс-ситуация «Расчет сетевого графика» 3. Расчет ранних сроков наступления событий (по формуле (1)). t P (1)= t P (2)=max{t P (1)+t(1, 2)}=max{ }= t P (3)=max{t P (2)+t(2, 3)}=max{ }= t P (5)=max{t P (4)+t(4, 5)}=max{ }= t P (6)=max{t P (5)+t(5, 6)}=max{ }= t P (8)=max{t P (7)+t(7, 8)}=max{ }= 4. Расчет поздних сроков наступления событий (по формуле (2)). t п (8)=t р (8)= t п (7)=min{t п (8)-t(7, 8)}=min{ }= t п (6)=min{t п (7)-t(6, 7)}=min{ }= t п (4)=min{t п (5)-t(4, 5)}=min{ }= t п (3)=min{t п (4)-t(3, 4)}=min{ }= t п (1)=min{t п (2)-t(1, 2)}=min{ }= Полученные результаты заносятся на сетевой график в соответствующие секторы 00 1 0 2 4 5 7 8 3 6 Сетевой график технологического процесса 0. 300. 10 0. 40 2. 30 0. 40 0. 10 I II V VIIV III max )4, 3(t)3(t )4, 2(t)2(t max)4(t ðð ð max )7, 6(t)6(t )7, 5(t)5(t max)7(t ð ð ð min )6, 5(t)6(t )7, 5(t)7(t min)5(t n n n min )3, 2(t)3(t )4, 2(t)4(t min)2(t n n n
Кейс-ситуация «Расчет сетевого графика» 3. Расчет ранних сроков наступления событий (по формуле (1)). t P (1)= t P (2)=max{t P (1)+t(1, 2)}=max{ }= t P (3)=max{t P (2)+t(2, 3)}=max{ }= t P (5)=max{t P (4)+t(4, 5)}=max{ }= t P (6)=max{t P (5)+t(5, 6)}=max{ }= t P (8)=max{t P (7)+t(7, 8)}=max{ }= 4. Расчет поздних сроков наступления событий (по формуле (2)). t п (8)=t р (8)= t п (7)=min{t п (8)-t(7, 8)}=min{ }= t п (6)=min{t п (7)-t(6, 7)}=min{ }= t п (4)=min{t п (5)-t(4, 5)}=min{ }= t п (3)=min{t п (4)-t(3, 4)}=min{ }= t п (1)=min{t п (2)-t(1, 2)}=min{ }= Полученные результаты заносятся на сетевой график в соответствующие секторы 00 1 0 2 4 5 7 8 3 6 Сетевой график технологического процесса 0. 300. 10 0. 40 2. 30 0. 40 0. 10 I II V VIIV III max )4, 3(t)3(t )4, 2(t)2(t max)4(t ðð ð max )7, 6(t)6(t )7, 5(t)5(t max)7(t ð ð ð min )6, 5(t)6(t )7, 5(t)7(t min)5(t n n n min )3, 2(t)3(t )4, 2(t)4(t min)2(t n n n
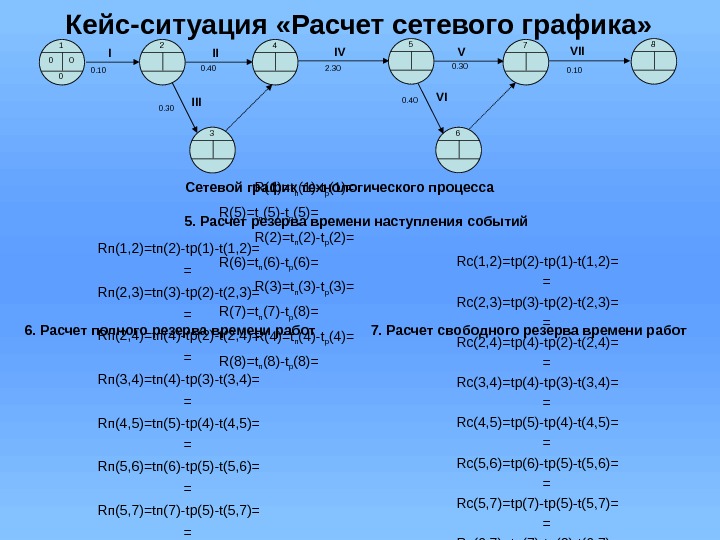
 Кейс-ситуация «Расчет сетевого графика» 5. Расчет резерва времени наступления событий R(1)=t п (1)-t р (1)= R(5)=t п (5)-t р (5)= R(2)=t п (2)-t р (2)= R(6)=t п (6)-t р (6)= R(3)=t п (3)-t р (3)= R(7)=t п (7)-t р (8)= R(4)=t п (4)-t р (4)= R(8)=t п (8)-t р (8)=6. Расчет полного резерва времени работ Rп(1, 2)=tп(2)-tр(1)-t(1, 2)= = Rп(2, 3)=tп(3)-tр(2)-t(2, 3)= = Rп(2, 4)=tп(4)-tр(2)-t(2, 4)= = Rп(3, 4)=tп(4)-tр(3)-t(3, 4)= = Rп(4, 5)=tп(5)-tр(4)-t(4, 5)= = Rп(5, 6)=tп(6)-tр(5)-t(5, 6)= = Rп(5, 7)=tп(7)-tр(5)-t(5, 7)= = Rп(6, 7)=tп(7)-tр(6)-t(6, 7)= = Rп(7, 8)=tп(8)-tр(7)-t(7, 8)= = 7. Расчет свободного резерва времени работ Rс(1, 2)=tр(2)-tр(1)-t(1, 2)= = Rс(2, 3)=tр(3)-tр(2)-t(2, 3)= = Rс(2, 4)=tр(4)-tр(2)-t(2, 4)= = Rс(3, 4)=tр(4)-tр(3)-t(3, 4)= = Rс(4, 5)=tр(5)-tр(4)-t(4, 5)= = Rс(5, 6)=tр(6)-tр(5)-t(5, 6)= = Rс(5, 7)=tр(7)-tр(5)-t(5, 7)= = Rс(6, 7)=tр(7)-tр(6)-t(6, 7)= = Rс(7, 8)=tр(8)-tр(7)-t(7, 8)= =00 1 0 2 4 5 7 8 3 6 Сетевой график технологического процесса 0. 300. 10 0. 40 2. 30 0. 40 0. 10 I II V VIIV III
Кейс-ситуация «Расчет сетевого графика» 5. Расчет резерва времени наступления событий R(1)=t п (1)-t р (1)= R(5)=t п (5)-t р (5)= R(2)=t п (2)-t р (2)= R(6)=t п (6)-t р (6)= R(3)=t п (3)-t р (3)= R(7)=t п (7)-t р (8)= R(4)=t п (4)-t р (4)= R(8)=t п (8)-t р (8)=6. Расчет полного резерва времени работ Rп(1, 2)=tп(2)-tр(1)-t(1, 2)= = Rп(2, 3)=tп(3)-tр(2)-t(2, 3)= = Rп(2, 4)=tп(4)-tр(2)-t(2, 4)= = Rп(3, 4)=tп(4)-tр(3)-t(3, 4)= = Rп(4, 5)=tп(5)-tр(4)-t(4, 5)= = Rп(5, 6)=tп(6)-tр(5)-t(5, 6)= = Rп(5, 7)=tп(7)-tр(5)-t(5, 7)= = Rп(6, 7)=tп(7)-tр(6)-t(6, 7)= = Rп(7, 8)=tп(8)-tр(7)-t(7, 8)= = 7. Расчет свободного резерва времени работ Rс(1, 2)=tр(2)-tр(1)-t(1, 2)= = Rс(2, 3)=tр(3)-tр(2)-t(2, 3)= = Rс(2, 4)=tр(4)-tр(2)-t(2, 4)= = Rс(3, 4)=tр(4)-tр(3)-t(3, 4)= = Rс(4, 5)=tр(5)-tр(4)-t(4, 5)= = Rс(5, 6)=tр(6)-tр(5)-t(5, 6)= = Rс(5, 7)=tр(7)-tр(5)-t(5, 7)= = Rс(6, 7)=tр(7)-tр(6)-t(6, 7)= = Rс(7, 8)=tр(8)-tр(7)-t(7, 8)= =00 1 0 2 4 5 7 8 3 6 Сетевой график технологического процесса 0. 300. 10 0. 40 2. 30 0. 40 0. 10 I II V VIIV III
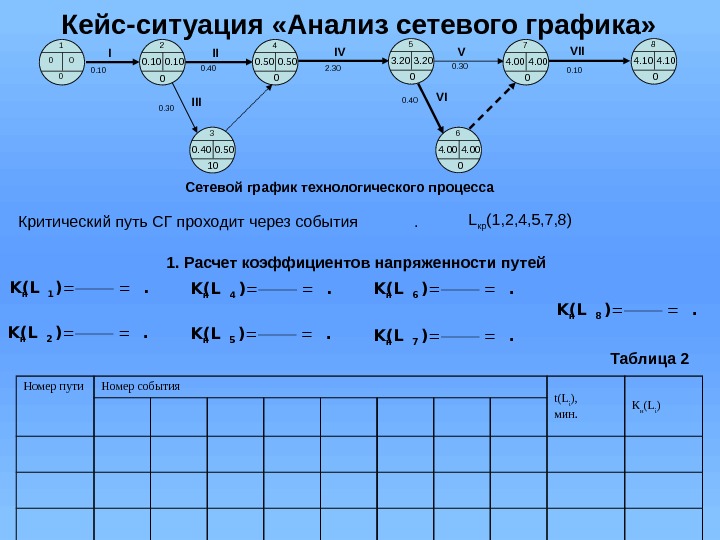
 Кейс-ситуация «Анализ сетевого графика» Критический путь СГ проходит через события . L кр (1, 2, 4, 5, 7, 8) Номер пути Номер события t(L i ), мин. К н (L i )1. Расчет коэффициентов напряженности путей Таблица 2 00 1 0 0. 10 2 0 0. 50 4 0 3. 20 5 0 4. 00 7 0 4. 10 8 0 0. 500. 40 3 10 4. 00 6 0 Сетевой график технологического процесса 0. 300. 10 0. 40 2. 30 0. 40 0. 10 I II V VIIV III. )(LK 1 н . )(LK 2 н . )(LK 4 н . )(LK 5 н . )(LK 6 н . )(LK 7 н . )(LK 8 н
Кейс-ситуация «Анализ сетевого графика» Критический путь СГ проходит через события . L кр (1, 2, 4, 5, 7, 8) Номер пути Номер события t(L i ), мин. К н (L i )1. Расчет коэффициентов напряженности путей Таблица 2 00 1 0 0. 10 2 0 0. 50 4 0 3. 20 5 0 4. 00 7 0 4. 10 8 0 0. 500. 40 3 10 4. 00 6 0 Сетевой график технологического процесса 0. 300. 10 0. 40 2. 30 0. 40 0. 10 I II V VIIV III. )(LK 1 н . )(LK 2 н . )(LK 4 н . )(LK 5 н . )(LK 6 н . )(LK 7 н . )(LK 8 н
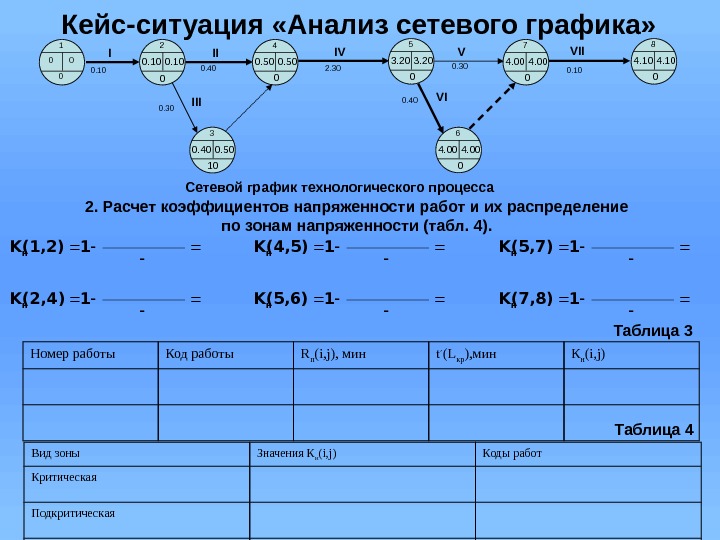
 Кейс-ситуация «Анализ сетевого графика» 2. Расчет коэффициентов напряженности работ и их распределение по зонам напряженности (табл. 4). Номер работы Код работы R п (i, j), мин t ׳ (L кр ), мин К н (i, j) Таблица 3 Вид зоны Значения К н (i, j) Коды работ Критическая Подкритическая Зона резервов Таблица 4 00 1 0 0. 10 2 0 0. 50 4 0 3. 20 5 0 4. 00 7 0 4. 10 8 0 0. 500. 40 3 10 4. 00 6 0 Сетевой график технологического процесса 0. 300. 10 0. 40 2. 30 0. 40 0. 10 I II V VIIV III 1(1, 2)K н 1(2, 4)K н 1(4, 5)K н 1(5, 6)K н 1(5, 7)K н 1(7, 8)K н
Кейс-ситуация «Анализ сетевого графика» 2. Расчет коэффициентов напряженности работ и их распределение по зонам напряженности (табл. 4). Номер работы Код работы R п (i, j), мин t ׳ (L кр ), мин К н (i, j) Таблица 3 Вид зоны Значения К н (i, j) Коды работ Критическая Подкритическая Зона резервов Таблица 4 00 1 0 0. 10 2 0 0. 50 4 0 3. 20 5 0 4. 00 7 0 4. 10 8 0 0. 500. 40 3 10 4. 00 6 0 Сетевой график технологического процесса 0. 300. 10 0. 40 2. 30 0. 40 0. 10 I II V VIIV III 1(1, 2)K н 1(2, 4)K н 1(4, 5)K н 1(5, 6)K н 1(5, 7)K н 1(7, 8)K н
 Преимущества методов сетевого планирования • Первым и самым главным является возможность определить минимальную длительность проекта; • с помощью метода критического пути можно определить, сроки выполнения каких работ являются наиболее важными для своевременного выполнения проекта. Соответственно, для оставшихся работ определяется резерв дополнительного времени, который можно затратить по своему усмотрению; • используя резерв времени, можно «маневрировать» сроками выполнения работ, избегая как чрезмерной, так и недостаточной загрузки рабочих ресурсов. Благодаря этому можно сократить общее количество задействованных рабочих ресурсов (а иногда и материальных – топлива, например) и, таким образом, сэкономить бюджет проекта; • благодаря сетевому графику с высокой степенью уверенности провести оценку, к каким последствиям приведет задержка в выполнении той или иной работы и, соответственно, направить максимальные усилия на устранение задержек критических для проекта; • на любой момент времени выполнения проекта для любого из его участников можно определить вид и объем работ, который ему следует выполнять. Соответственно, при правильном подходе всегда можно найти виновного в срыве сроков проекта.
Преимущества методов сетевого планирования • Первым и самым главным является возможность определить минимальную длительность проекта; • с помощью метода критического пути можно определить, сроки выполнения каких работ являются наиболее важными для своевременного выполнения проекта. Соответственно, для оставшихся работ определяется резерв дополнительного времени, который можно затратить по своему усмотрению; • используя резерв времени, можно «маневрировать» сроками выполнения работ, избегая как чрезмерной, так и недостаточной загрузки рабочих ресурсов. Благодаря этому можно сократить общее количество задействованных рабочих ресурсов (а иногда и материальных – топлива, например) и, таким образом, сэкономить бюджет проекта; • благодаря сетевому графику с высокой степенью уверенности провести оценку, к каким последствиям приведет задержка в выполнении той или иной работы и, соответственно, направить максимальные усилия на устранение задержек критических для проекта; • на любой момент времени выполнения проекта для любого из его участников можно определить вид и объем работ, который ему следует выполнять. Соответственно, при правильном подходе всегда можно найти виновного в срыве сроков проекта.
