Смілянська загальноосвітня школи І ІІІ ступенів

Смілянська загальноосвітня школи І – ІІІ ступенів № 11 Смілянської міської ради Черкаської області Паралельність прямих і площин у просторі Геометрія, 10 клас Профільний рівень Учитель Русецька Т. В.

Основні теми розділу • • Мимобіжні та паралельні прямі Паралельність прямої та площини Паралельність площин Паралельне проектування та його властивості • Зображення фігур у стереометрії • Методи побудови перерізів многогранників

Мета: вчити • Формулювати означення паралельних і мимобіжних прямих, паралельних прямої і площини, паралельних площин; ознаки паралельності прямих і площин; властивості паралельності прямих і площин. • Класифікувати взаємне розміщення прямих, прямих і площин, площин у просторі. • Знаходити і зображати паралельні прямі, прямі та площини на малюнках, будувати зображення фігур. • Розв’язувати задачі на застосування властивостей та ознак паралельності прямих і площин. • Застосовувати метод слідів та проекцій для побудови перерізів многогранників.

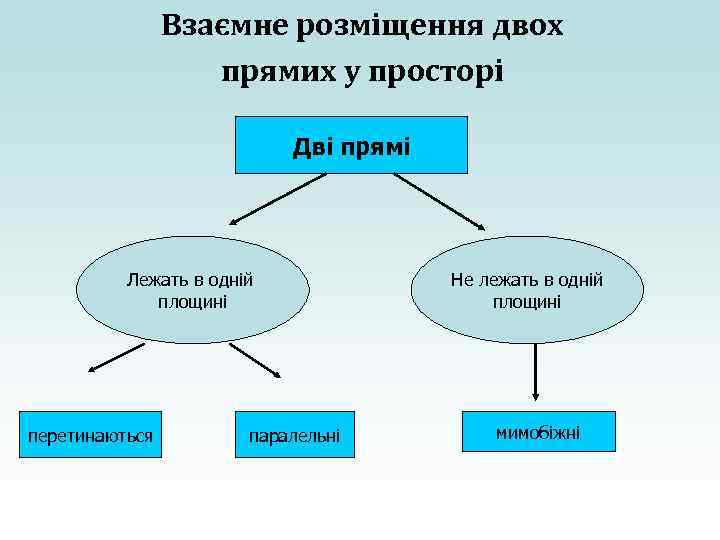Взаємне розміщення двох прямих у просторі Дві прямі Лежать в одній площині перетинаються паралельні Не лежать в одній площині мимобіжні

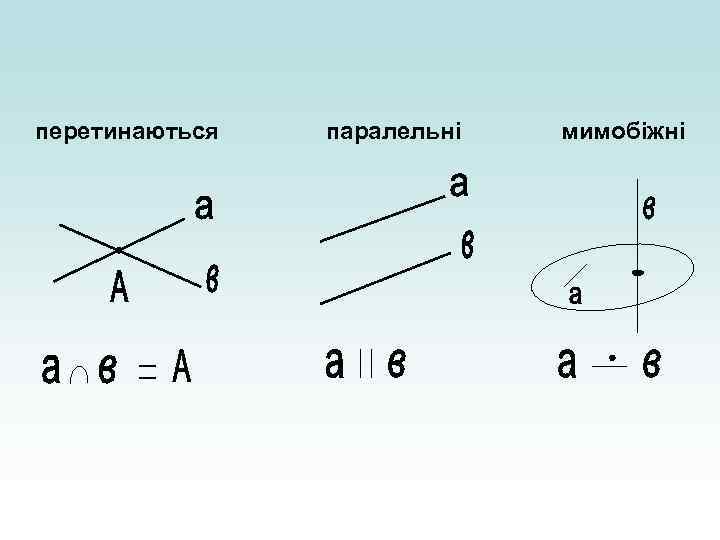перетинаються паралельні мимобіжні

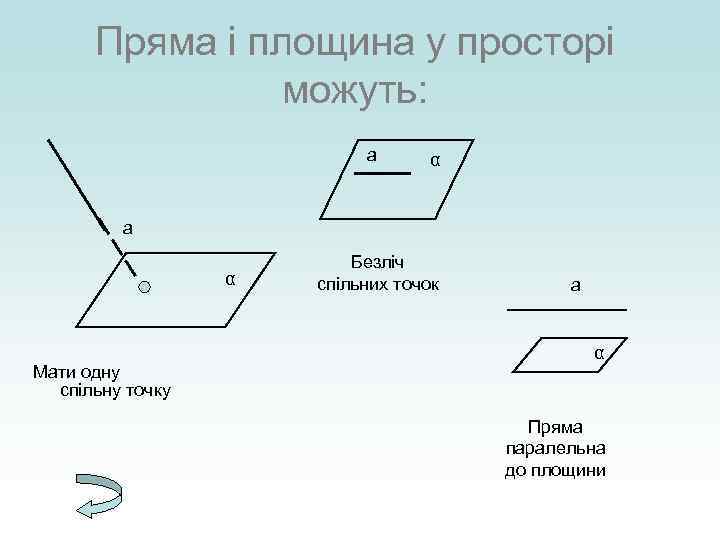Пряма і площина у просторі можуть: а α Мати одну спільну точку Безліч спільних точок а α Пряма паралельна до площини

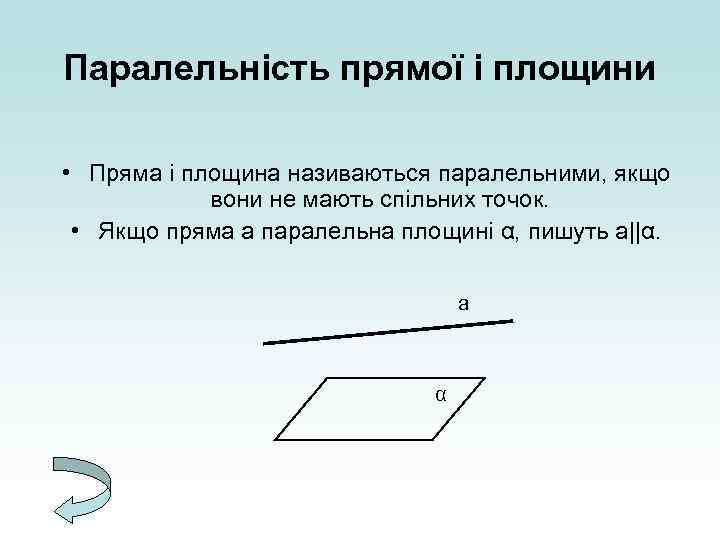Паралельність прямої і площини • Пряма і площина називаються паралельними, якщо вони не мають спільних точок. • Якщо пряма а паралельна площині α, пишуть а||α. а α

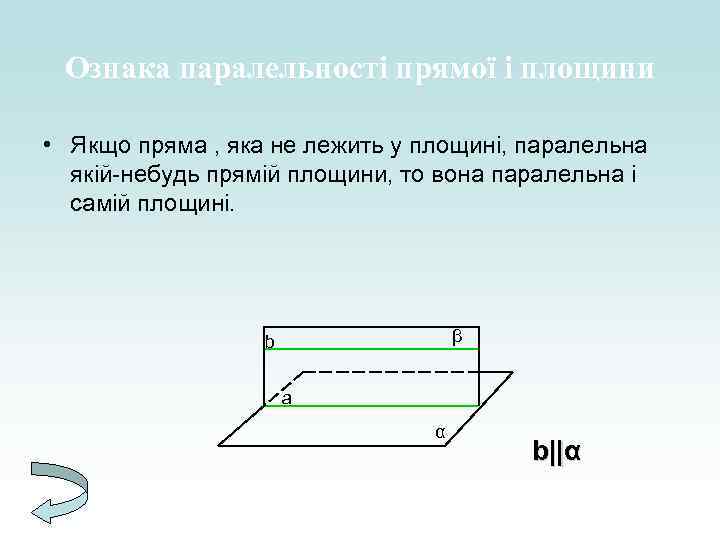Ознака паралельності прямої і площини • Якщо пряма , яка не лежить у площині, паралельна якій-небудь прямій площини, то вона паралельна і самій площині. β b a α b||α

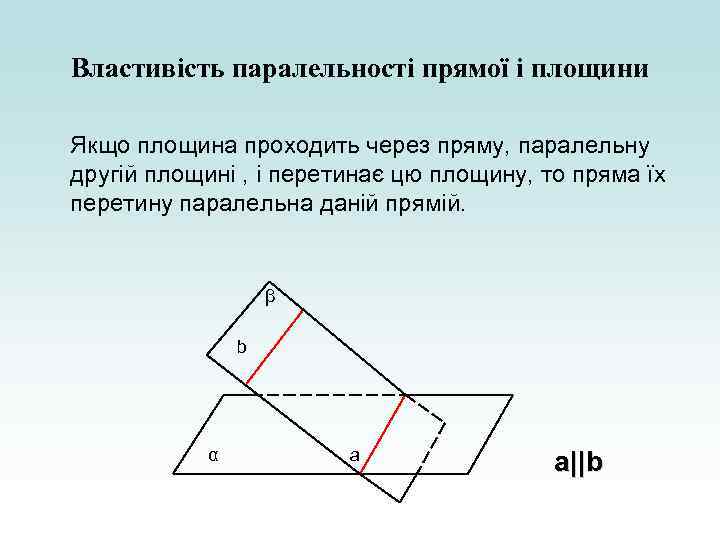Властивість паралельності прямої і площини Якщо площина проходить через пряму, паралельну другій площині , і перетинає цю площину, то пряма їх перетину паралельна даній прямій. β b α a a||b

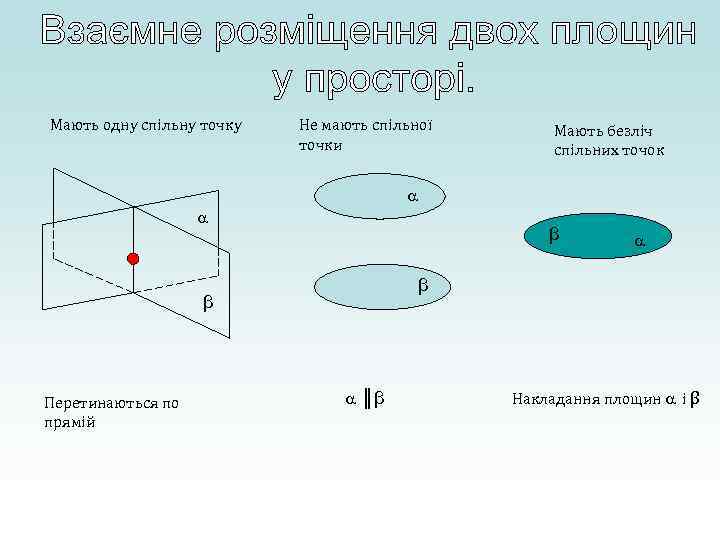Мають одну спільну точку Не мають спільної точки Мають безліч спільних точок β β β Перетинаються по прямій ║β Накладання площин і β

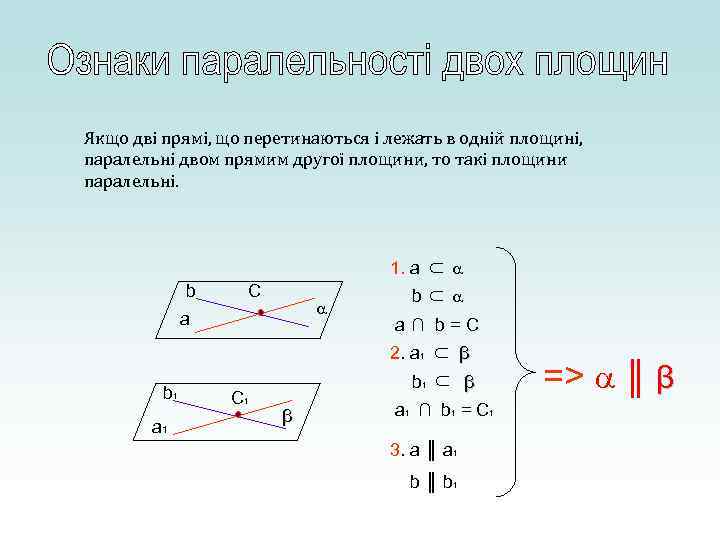1. a C a b a 1 C 1 β β a 1 ∩ b 1 = C 1 b 1 β a ∩ b=C 2. a 1 b 1 ∩ ∩ b ∩ ∩ Якщо дві прямі, що перетинаються і лежать в одній площині, паралельні двом прямим другої площини, то такі площини паралельні. 3. a ║ а 1 b ║ b 1 => ║ β

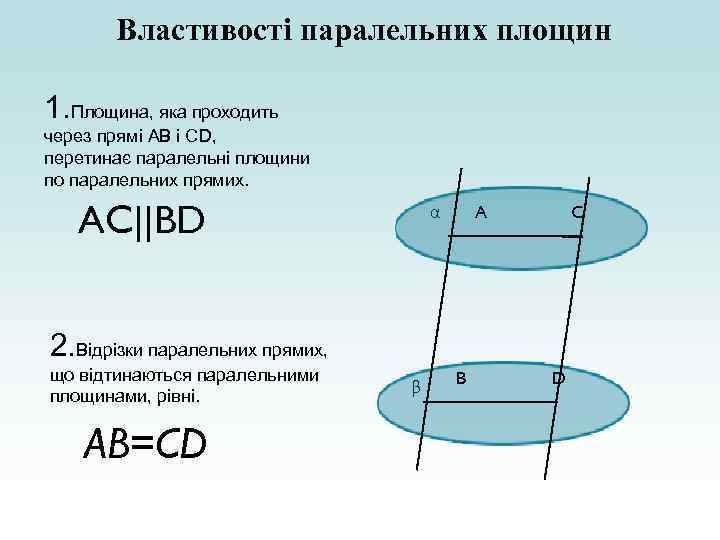Властивості паралельних площин 1. Площина, яка проходить через прямі АВ і СD, перетинає паралельні площини по паралельних прямих. AC||BD α A C 2. Відрізки паралельних прямих, що відтинаються паралельними площинами, рівні. AB=CD β B D

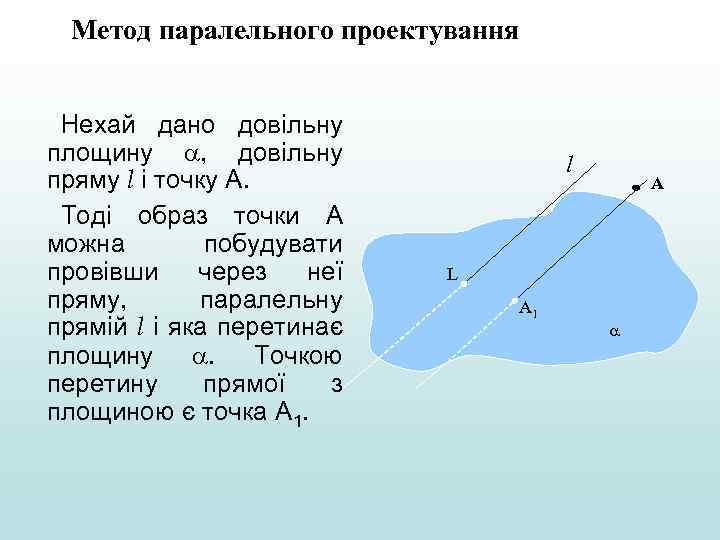Метод паралельного проектування Нехай дано довільну площину , довільну пряму l і точку А. Тоді образ точки А можна побудувати провівши через неї пряму, паралельну прямій l і яка перетинає площину . Точкою перетину прямої з площиною є точка А 1. l А L А 1

Зображення Оригінал B K C A M D B 1 A 1 K 1 M 1 C 1 D 1

B C D А Оригінал B 1 C 1 D 1 А 1 Зображення

Оригінал B K Зображення C B 1 A M D A 1 K 1 M 1 AB : BC = 1 : 2 A 1 B 1 : B 1 C 1 = 1 : 2 CD : AD = 1 : 2 C 1 D 1 : A 1 B 1 = 1 : 2 BK : KC = B 1 K 1 : K 1 C 1 AM : MD = A 1 M 1 : M 1 D 1 C 1 D 1

Тестове завдання 1. Точка М не лежить у площині прямокутника ABCD. Яке взаємне розташування прямих МА і СD ? А) Перетинаються; Б) паралельні; В) мимобіжні; Г) паралельні або мимобіжні. 2. Пряма а паралельна площині , пряма b належить площині . Яким може бути взаємне розміщення прямих а і b? А) Паралельні; Б) перетинаються; В) мимобіжні; Г) мимобіжні або паралельні. 3. Точка М лежить поза площиною трикутника АВС. Точки К, Р, Е і D – середини відрізків МА, АВ, МС і ВС відповідно. Яке взаємне розміщення прямих КР і ЕD? А) Перетинаються; Б) мимобіжні; В) паралельні; Г) мимобіжні або перетинаються.

4. Сторона АВ паралелограма ABCD належить площині , а сторона СD не належить цій площині. Яке взаємне розміщення прямої СD і площини ? А) пряма СD перетинає площину ; Б) пряма СD паралельна площині ; В) пряма СD лежить у площині. 5. Пряма а паралельна площині . Скільки площин, паралельних площині можна провести через пряму а? А) Одну; Б) дві; И) жодної; Г) безліч. 6. Як розташовані площини і , якщо пряма а перетинає площину і паралельна площині ? А) Паралельні; Б) перетинаються; В) збігаються; Г) визначити неможливо. 7. Точка М не належить жодній із паралельних площин і. Скільки всього існує площин, які проходять через точку М і паралельні площинам і ? А) Одна; Б) дві; В) жодної; Г) безліч.

8. Площини і паралельні. Пряма а перетинає площину. Як розташована пряма а відносно площини ? А) Паралельна площині; Б) лежить у площині; В) перетинає площину; Г) визначити неможливо. 9. Основи трапеції паралельні площині. Яке взаємне розміщення площини трапеції і площини ? А) Перетинаються; Б) паралельні; В) збігаються; Г) визначити неможливо. 10. Площини і паралельні. Площина по прямій а , а з площиною перетинається з площиною - по прямій b. Яке взаємне розміщення прямих а і b? А) Перетинаються; Б) мимобіжні; В) паралельні; Г) визначити неможливо.

Відповіді до тесту 1 В , 2 Г , 3 В , 4 Б , 5 А , 6 Б , 7 А , 8 В , 9 А , 10 В

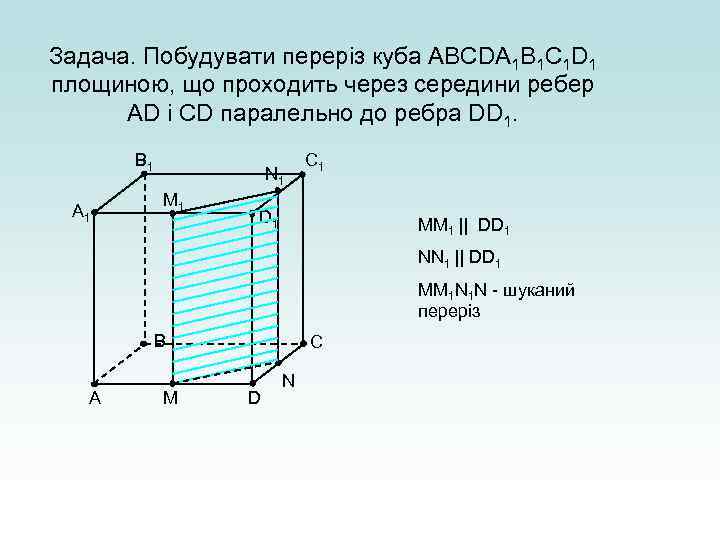Задача. Побудувати переріз куба АВСDА 1 В 1 С 1 D 1 площиною, що проходить через середини ребер АD і СD паралельно до ребра DD 1. В 1 А 1 N 1 М 1 С 1 D 1 ММ 1 || DD 1 NN 1 || DD 1 МM 1 N 1 N - шуканий переріз В А М С D N

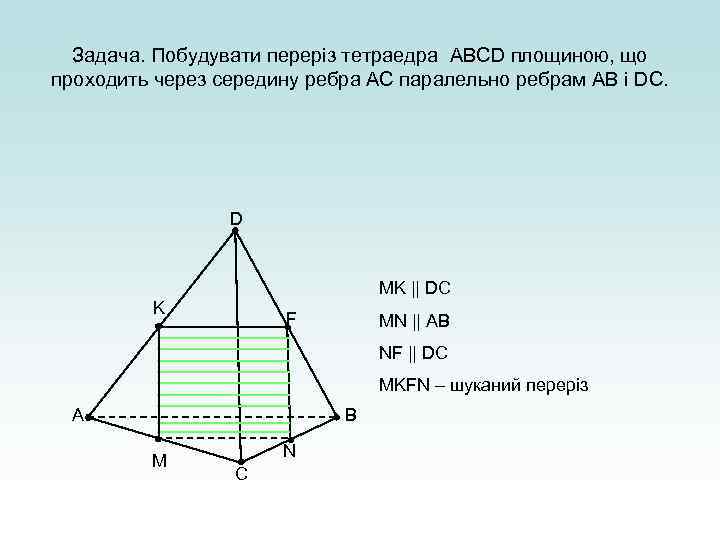Задача. Побудувати переріз тетраедра ABCD площиною, що проходить через середину ребра АС паралельно ребрам AB і DC. D MK || DC K F MN || AB NF || DC MKFN – шуканий переріз A B M N C

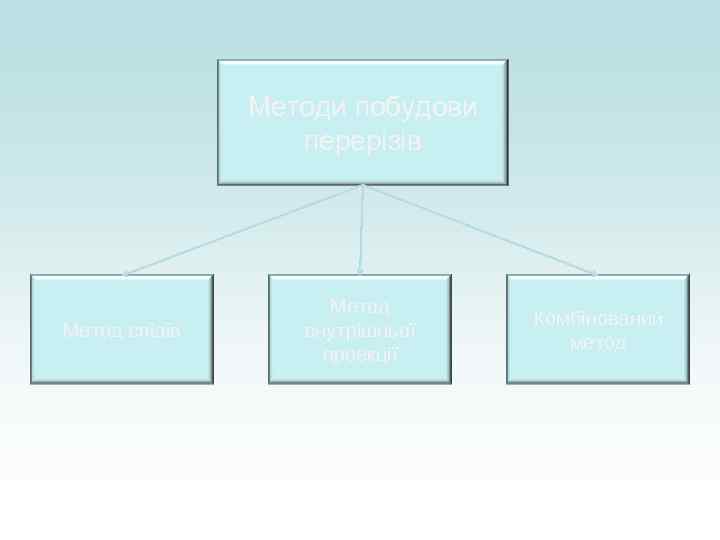Методи побудови перерізів Метод слідів Метод внутрішньої проекції Комбінований метод

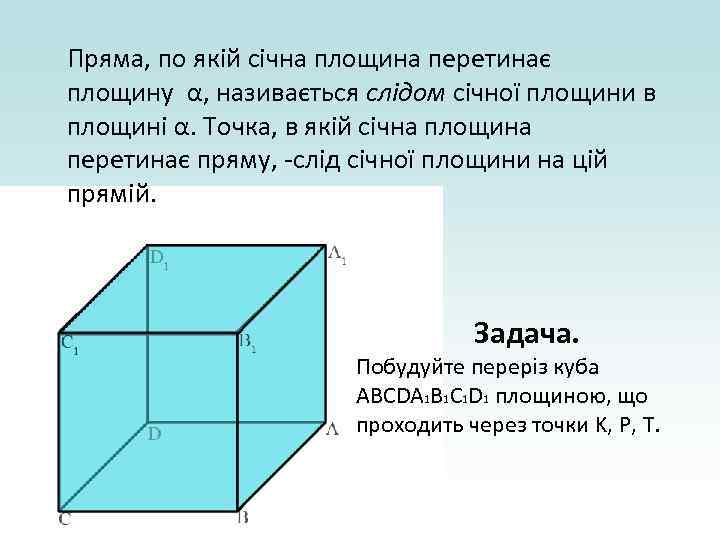Пряма, по якій січна площина перетинає площину α, називається слідом січної площини в площині α. Точка, в якій січна площина перетинає пряму, -слід січної площини на цій прямій. Задача. Побудуйте переріз куба ABCDA 1 B 1 C 1 D 1 площиною, що проходить через точки K, P, T.

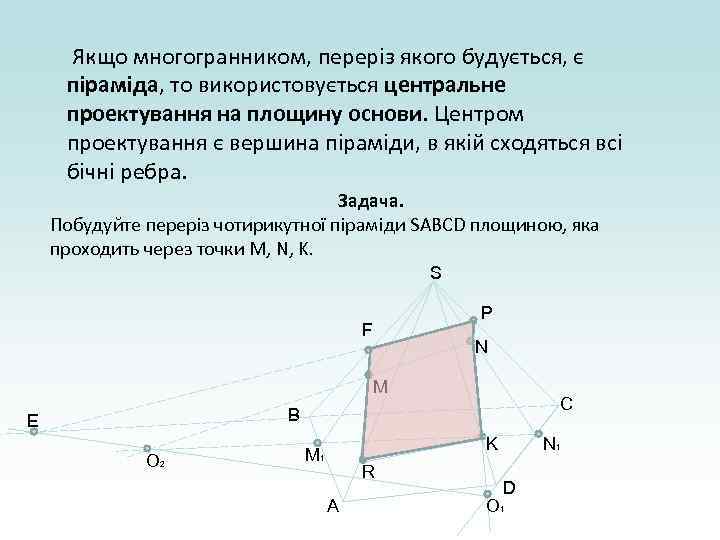Якщо многогранником, переріз якого будується, є піраміда, то використовується центральне проектування на площину основи. Центром проектування є вершина піраміди, в якій сходяться всі бічні ребра. Задача. Побудуйте переріз чотирикутної піраміди SABCD площиною, яка проходить через точки M, N, K. S P F N M C B E O 2 K M 1 R A N 1 D O 1

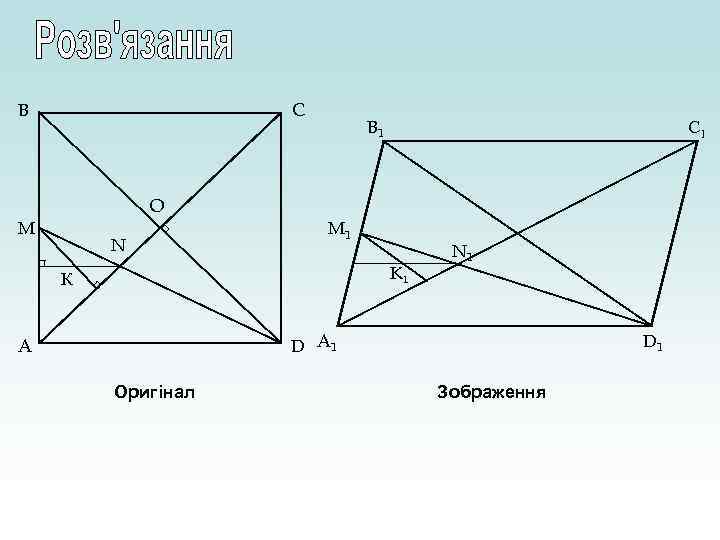
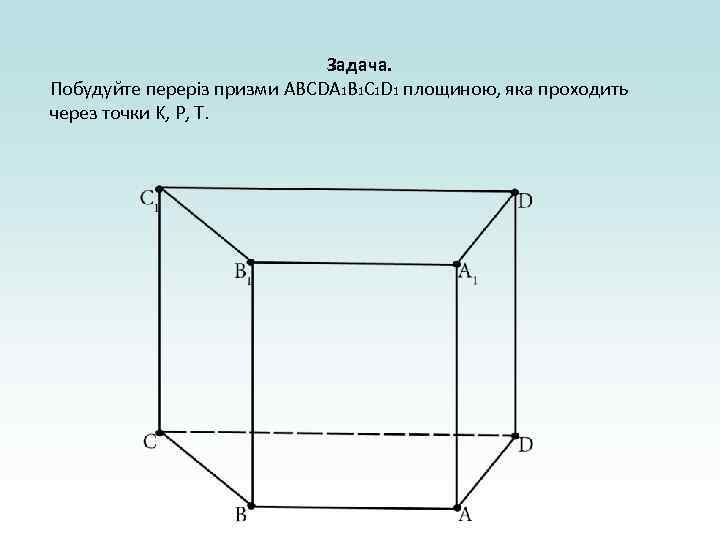Задача. Побудуйте переріз призми ABCDA 1 B 1 C 1 D 1 площиною, яка проходить через точки K, P, T.

Чотирикутник A 1 B 1 C 1 D 1 є зображенням квадрата. Точка М – середина АВ, AC і DM перетинаються у точці N. Побудувати зображення ортоцентра трикутника ANM.

B C B 1 C 1 O M N M 1 K 1 К N 1 D A 1 A Оригінал D 1 Зображення

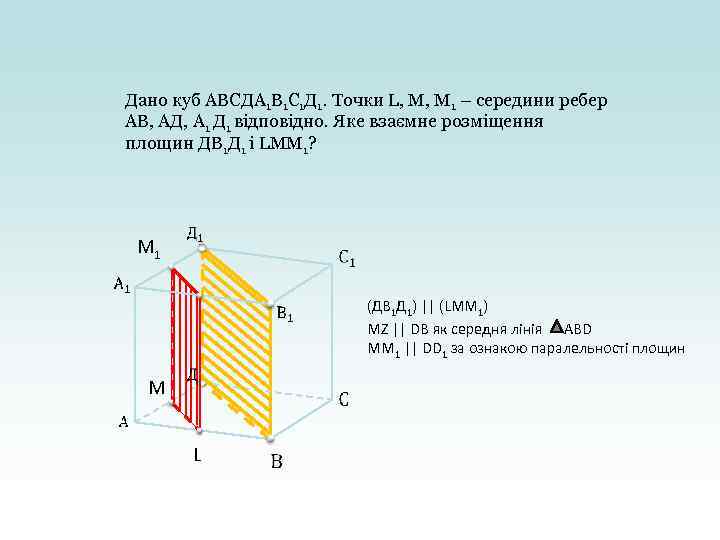Дано куб АВСДА 1 В 1 С 1 Д 1. Точки L, M, M 1 – cередини ребер АВ, АД, А 1 Д 1 відповідно. Яке взаємне розміщення площин ДВ 1 Д 1 і LMM 1? M 1 (ДВ 1 Д 1) || (LMM 1) MZ || DB як середня лінія ABD MM 1 || DD 1 за ознакою паралельності площин M L

Задача для самостійного розв’язування Дано прямокутниий паралелепіпед у якого АВ= , ВС= , =. Через вершину зроблено переріз паралелепіпеда, паралельний площині. Знайдіть площу цього перерізу. ,