Смежные углы Признаки равенства треугольников 1 По двум

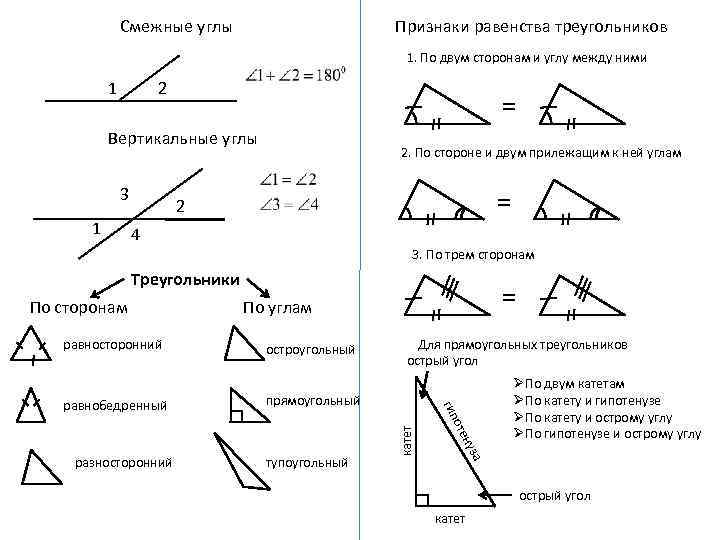Смежные углы Признаки равенства треугольников 1. По двум сторонам и углу между ними 1 2 = Вертикальные углы 3 1 2. По стороне и двум прилежащим к ней углам = 2 4 3. По трем сторонам Треугольники равносторонний Для прямоугольных треугольников острый угол прямоугольный а нуз тупоугольный оте разносторонний остроугольный гип равнобедренный = По углам катет По сторонам ØПо двум катетам ØПо катету и гипотенузе ØПо катету и острому углу ØПо гипотенузе и острому углу острый угол катет

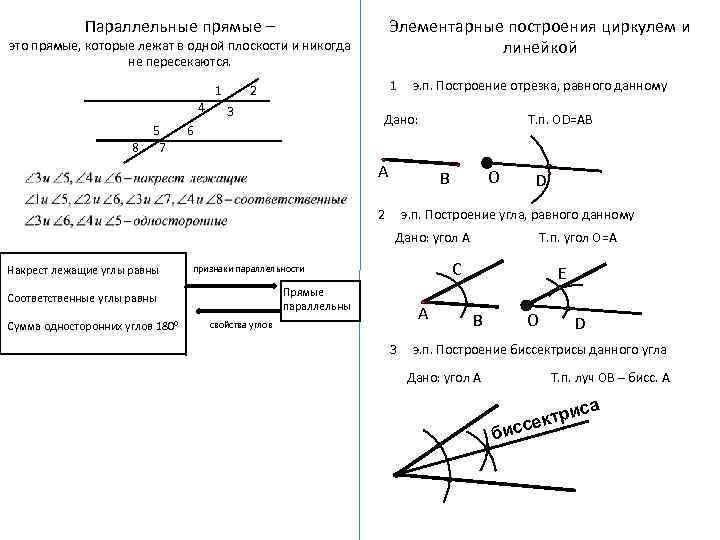Параллельные прямые – Элементарные построения циркулем и линейкой это прямые, которые лежат в одной плоскости и никогда не пересекаются. 4 8 5 7 1 1 2 3 э. п. Построение отрезка, равного данному Дано: 6 А Т. п. ОD=АВ О В 2 D э. п. Построение угла, равного данному Дано: угол А Накрест лежащие углы равны Сумма односторонних углов 180 0 С признаки параллельности Прямые параллельны Соответственные углы равны Т. п. угол О=А А свойства углов 3 E В О D э. п. Построение биссектрисы данного угла Дано: угол А Т. п. луч ОВ – бисс. А са б ри сект ис

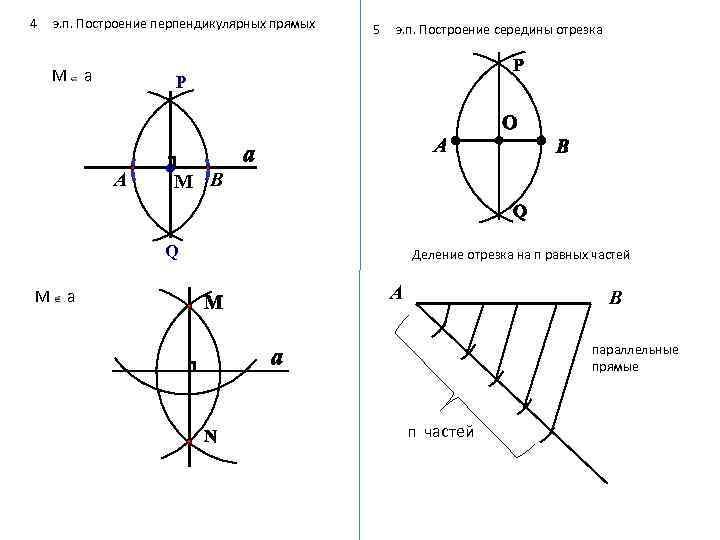4 э. п. Построение перпендикулярных прямых М а 5 э. п. Построение середины отрезка P P О А a А В М В Q Q М а Деление отрезка на п равных частей А М В параллельные прямые a N п частей

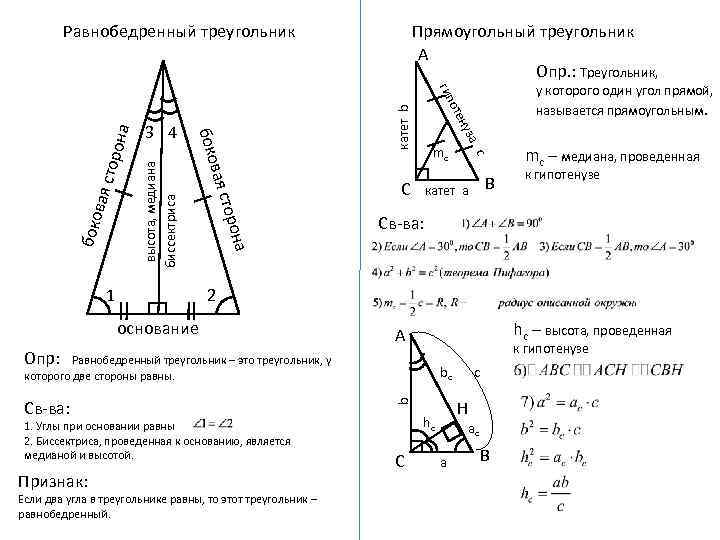высота, медиана биссектриса катет b торо н вая с с С а боко нуз mc В катет а mc – медиана, проведенная к гипотенузе Св-ва: 2 основание hc – высота, проведенная А к гипотенузе Опр: Равнобедренный треугольник – это треугольник, у которого две стороны равны. 1. Углы при основании равны 2. Биссектриса, проведенная к основанию, является медианой и высотой. Если два угла в треугольнике равны, то этот треугольник – равнобедренный. bc hc С c Н b Св-ва: Признак: у которого один угол прямой, называется прямоугольным. а н торо вая с 1 Прямоугольный треугольник А Опр. : Треугольник, оте гип 3 4 боко а Равнобедренный треугольник ac a В

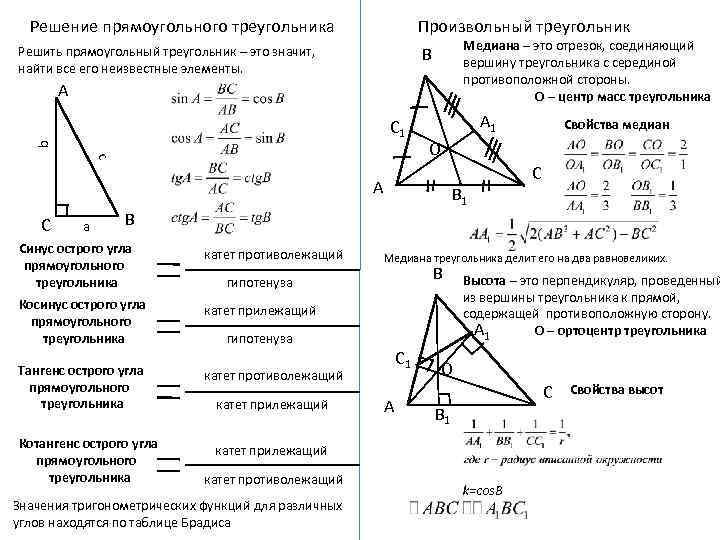Решение прямоугольного треугольника Произвольный треугольник Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. О – центр масс треугольника В Решить прямоугольный треугольник – это значит, найти все его неизвестные элементы. А b С 1 А 1 с О А С а В 1 В Синус острого угла прямоугольного треугольника катет противолежащий Косинус острого угла прямоугольного треугольника катет прилежащий Тангенс острого угла прямоугольного треугольника катет противолежащий Котангенс острого угла прямоугольного треугольника В гипотенуза С 1 А Высота – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону. О – ортоцентр треугольника А 1 О С В 1 катет прилежащий катет противолежащий Значения тригонометрических функций для различных углов находятся по таблице Брадиса С Медиана треугольника делит его на два равновеликих. гипотенуза катет прилежащий Свойства медиан k=соs. B Свойства высот

В С 1 А 1 О А Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. О – центр вписанной в треугольник окружности Соотношения между сторонами и углами произвольного треугольника В С В 1 c Свойства биссектрисы треугольника А Теорема косинусов a М N b С Теорема синусов В С 1 А А 1 О В 1 Срединный перпендикуляр– это прямая, перпендикулярная стороне треугольника, проходящая через ее середину О – центр описанной около треугольника окружности С Теорема о сумме углов треугольника. Неравенство треугольника. Напротив большей стороны треугольника лежит больший угол. Напротив большего угла треугольника лежит большая сторона. Средняя линия треугольника (MN) - это отрезок, соединяющий середины двух его сторон.

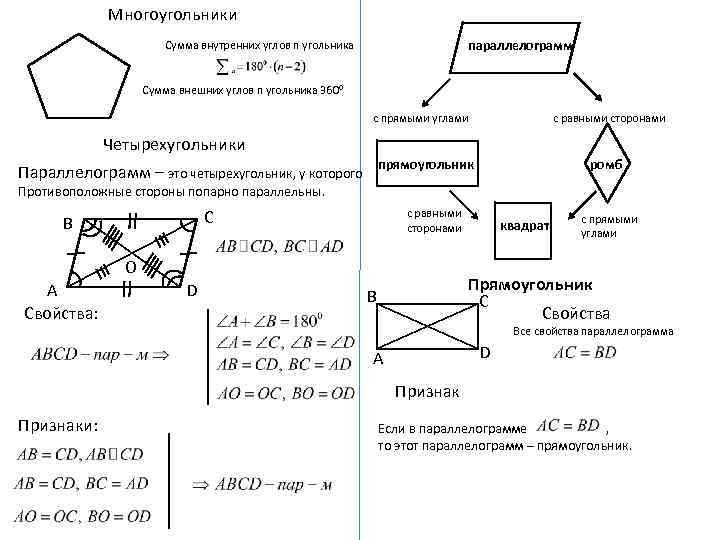Многоугольники параллелограмм Сумма внутренних углов n угольника Сумма внешних углов n угольника 3600 с прямыми углами с равными сторонами Четырехугольники прямоугольник Параллелограмм – это четырехугольник, у которого ромб Противоположные стороны попарно параллельны. С В с равными сторонами О А Cвойства: D квадрат с прямыми углами Прямоугольник С Свойства В Все свойства параллелограмма D А Признаки: Если в параллелограмме , то этот параллелограмм – прямоугольник.

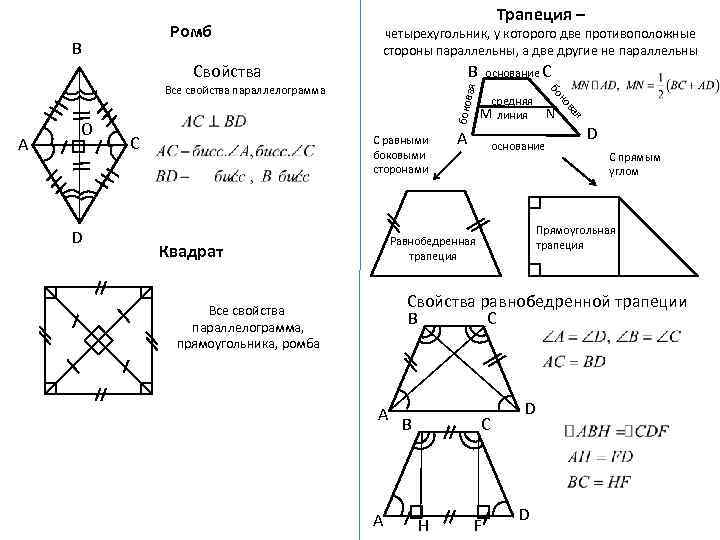Ромб В Трапеция – четырехугольник, у которого две противоположные стороны параллельны, а две другие не параллельны Свойства В ая боков С равными боковыми сторонами А основание D С прямым углом Прямоугольная трапеция Равнобедренная трапеция Квадрат N я ва D С средняя M линия ко А O бо Все свойства параллелограмма основание С Свойства равнобедренной трапеции В С Все свойства параллелограмма, прямоугольника, ромба А А В С H F D D

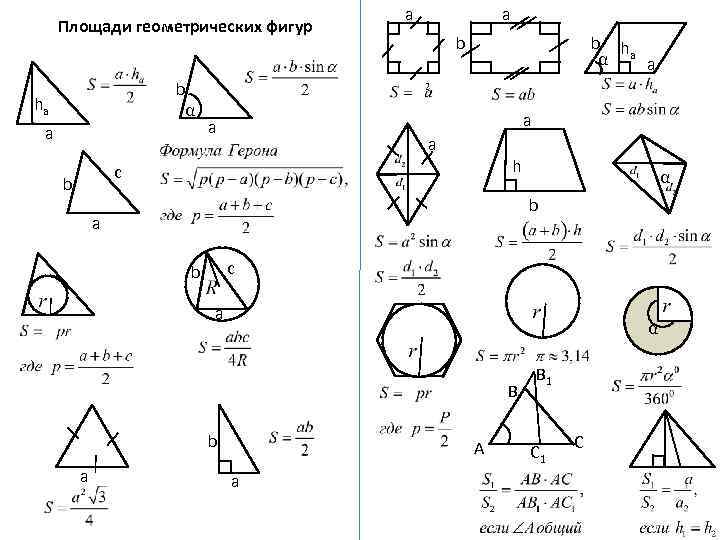Площади геометрических фигур b α hа а a a b b h α а a a h c b α b a c b a α В b a А a В 1 С

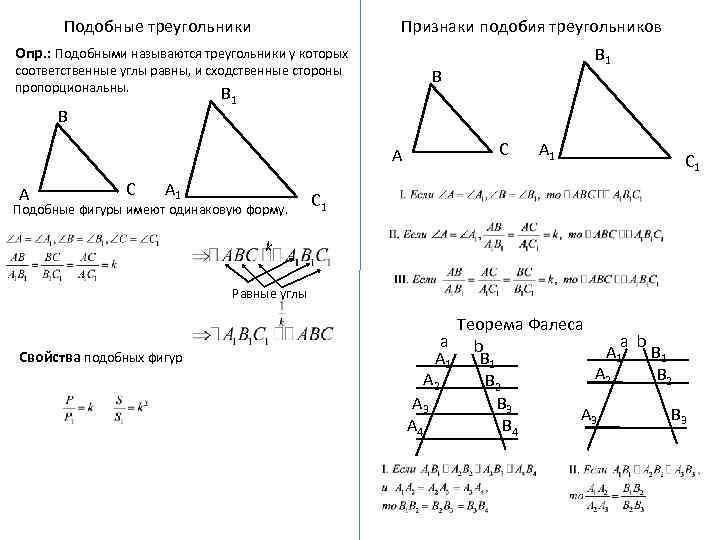Подобные треугольники Признаки подобия треугольников В 1 Опр. : Подобными называются треугольники у которых соответственные углы равны, и сходственные стороны пропорциональны. В В 1 В А А С А 1 Подобные фигуры имеют одинаковую форму. С А 1 С 1 k Равные углы Свойства подобных фигур Теорема Фалеса а b А 1 В 1 А 2 В 2 А 3 В 3 А 4 В 4

Свойства касательной к окружности (отрезков касательной) Окружность А С О D В Углы в окружности. О Свойство биссектрисы угла О Свойство серединного перпендикуляра М А А В D Е А В = А В С D С I = Е Е Н I В

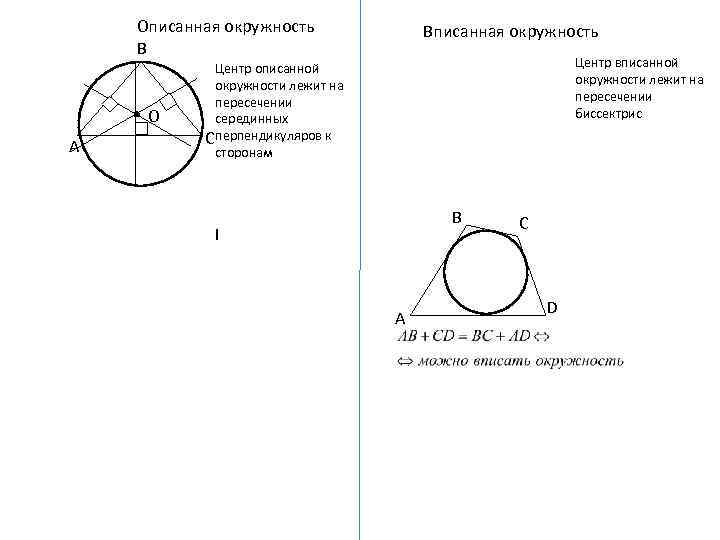Описанная окружность В О А Вписанная окружность Центр вписанной окружности лежит на пересечении биссектрис Центр описанной окружности лежит на пересечении серединных С перпендикуляров к сторонам В I А С D