fff1ea24f642ca6343a0d55a6bc6c8fb.ppt
- Количество слайдов: 18

Смежные и вертикальные углы
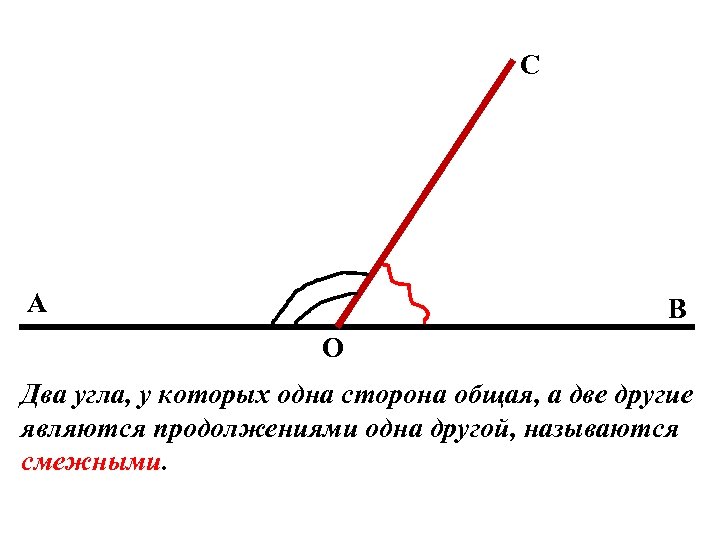
C A B O Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными.
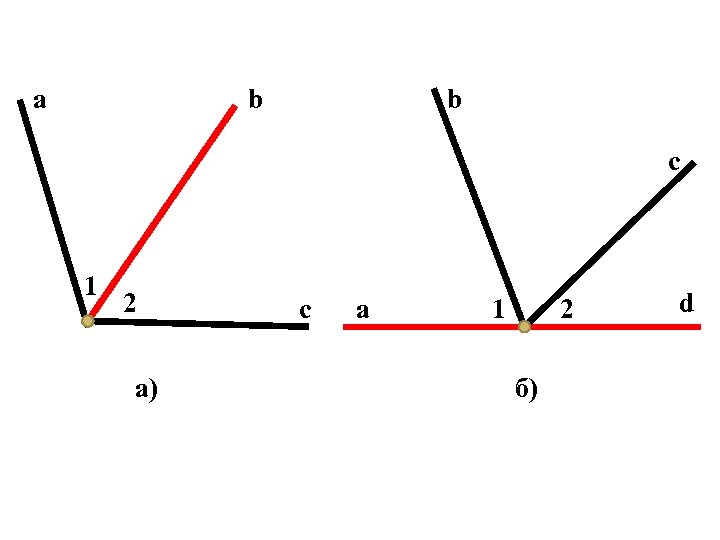
a b b c 1 2 а) c a 1 2 б) d
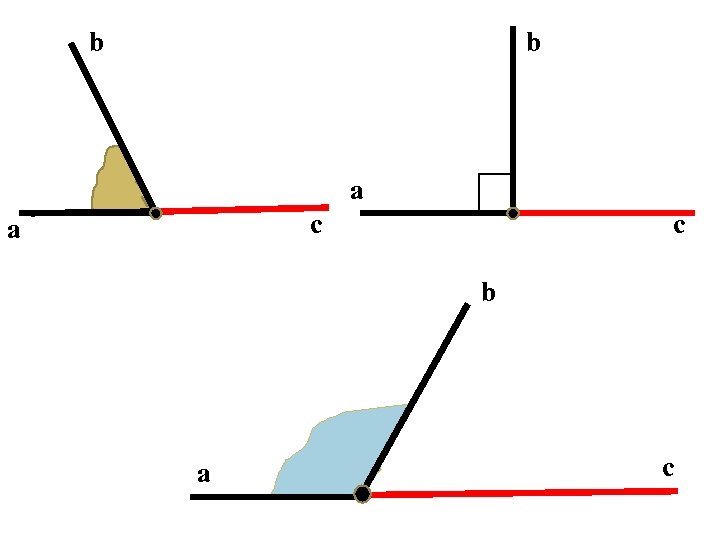
b b a c

b a Сумма смежных углов равна 1800. c Дано: <(ab) и <(bc)-смежные. Доказать, что <(ab) + <(bc)=1800. Доказательство: Луч b проходит между сторонами развернутого угла (ac) и делит его на два угла (ab) и (bc). Значит, <(ab) + <(bc)=<(ac)=1800.
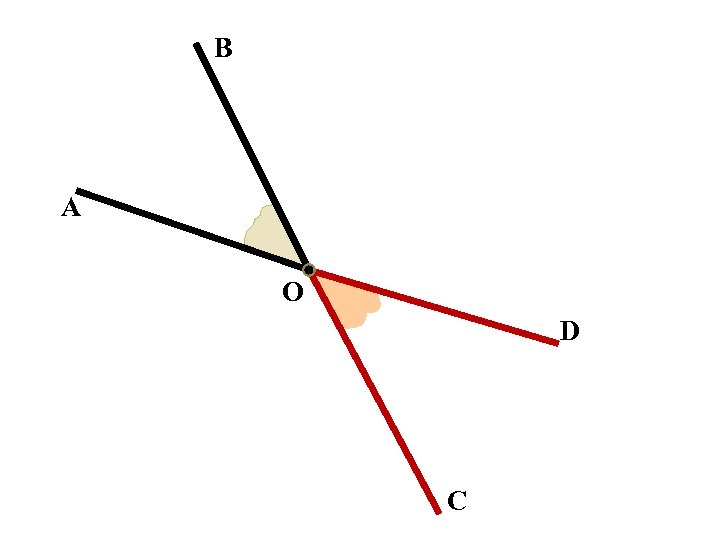
В А О D С
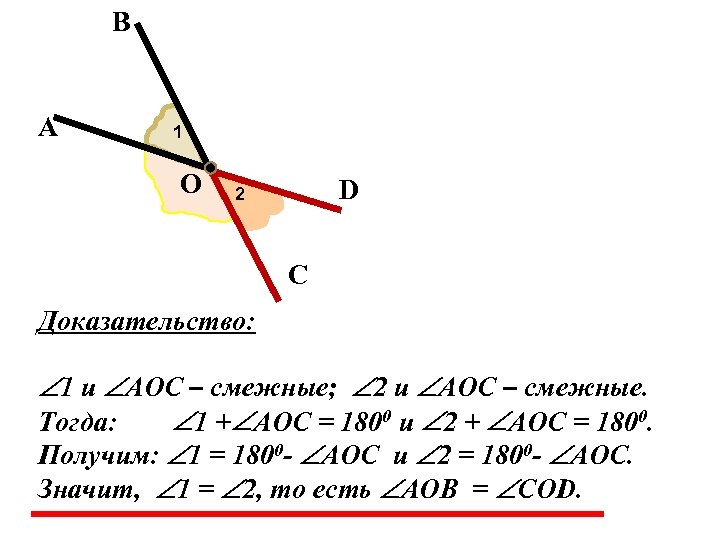
В А 1 О D 2 С Доказательство: 1 и AOC – смежные; 2 и AOC – смежные. Тогда: 1 + AOC = 1800 и 2 + AOC = 1800. Получим: 1 = 1800 - AOC и 2 = 1800 - AOC. Значит, 1 = 2, то есть AOB = COD.
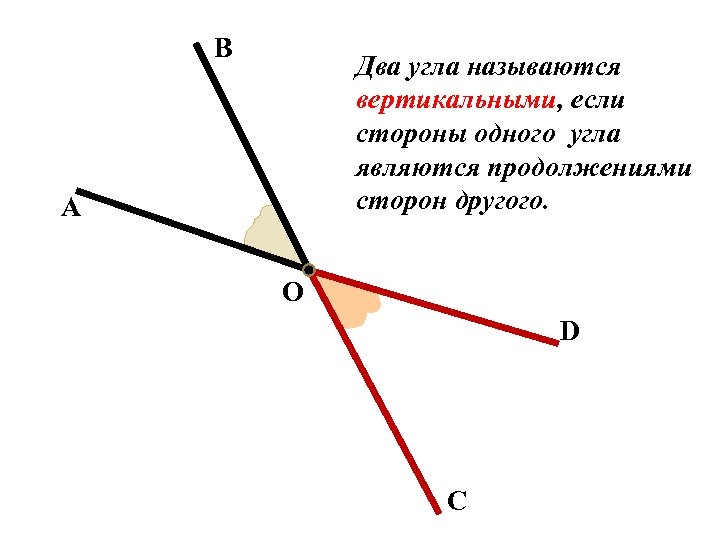
В Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого. А О D С
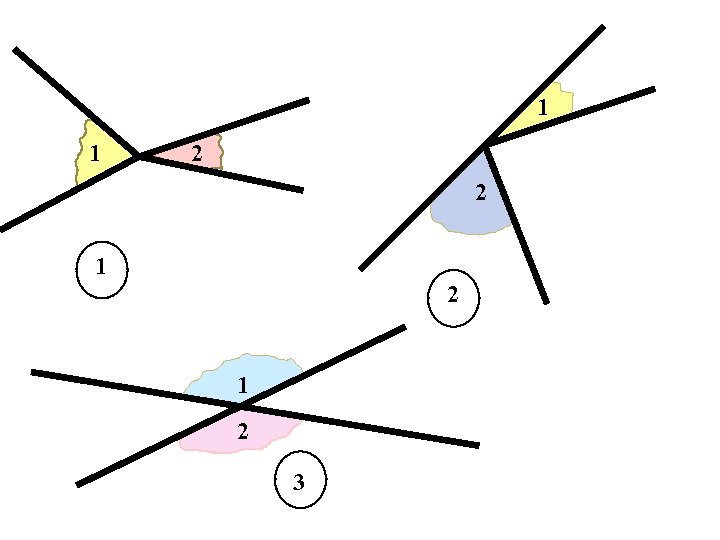
1 1 2 2 1 2 3

Задачи по готовым чертежам
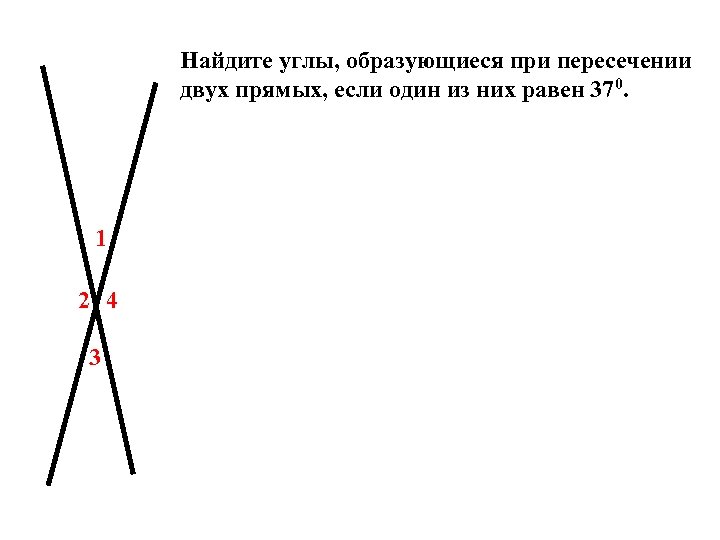
Найдите углы, образующиеся при пересечении двух прямых, если один из них равен 370. 1 2 4 3
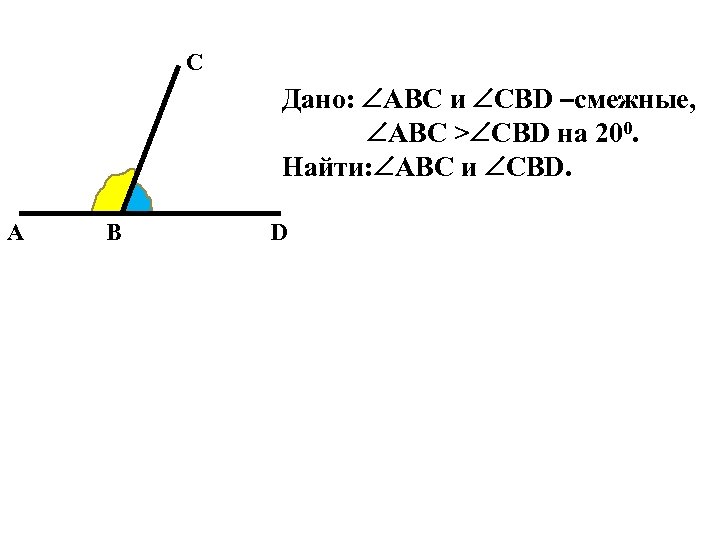
C Дано: ABC и CBD –смежные, ABC > CBD на 200. Найти: ABC и CBD. A B D
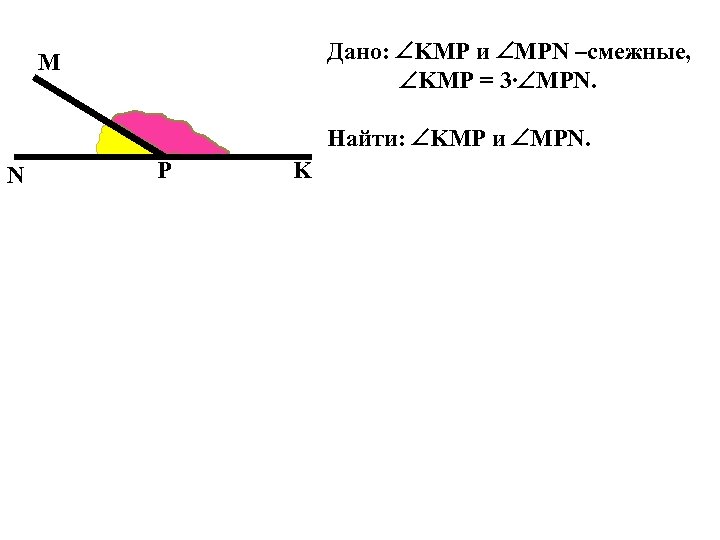
Дано: KMP и MPN –смежные, KMP = 3∙ MPN. M Найти: KMP и MPN. N P K
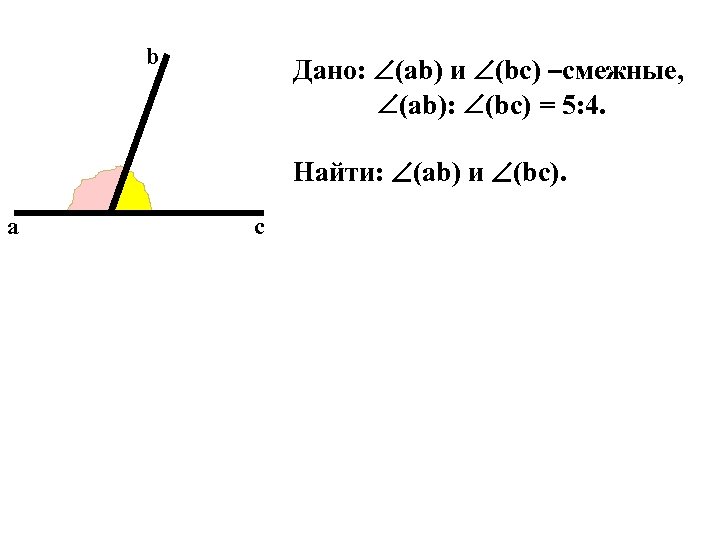
b Дано: (ab) и (bc) –смежные, (ab): (bc) = 5: 4. Найти: (ab) и (bc). a c
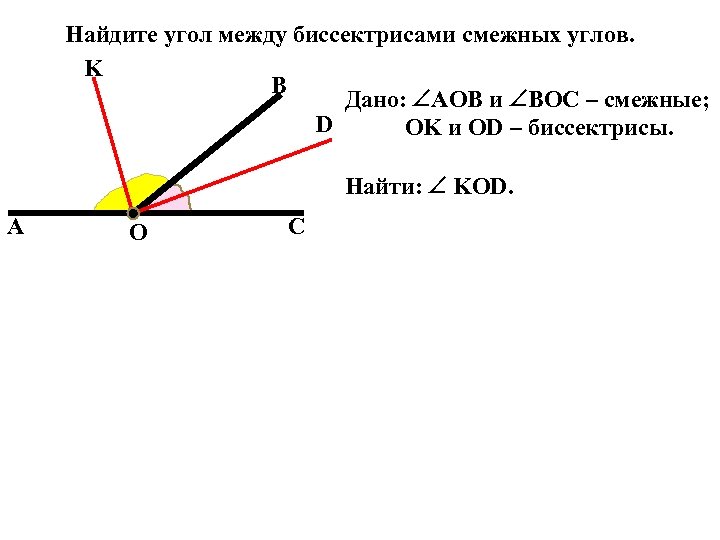
Найдите угол между биссектрисами смежных углов. K B Дано: AOB и BOC – смежные; D OK и OD – биссектрисы. Найти: KOD. A O C


Задание на дом: п. 11 № 55, 56, 61(а, г, д), № 64(а).
fff1ea24f642ca6343a0d55a6bc6c8fb.ppt