СЛУЧАЙНЫЕ ВЕЛИЧИНЫ ОСНОВНЫЕ ПОНЯТИЯ Случайная величина СВ величина

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

ОСНОВНЫЕ ПОНЯТИЯ Случайная величина (СВ)–величина, которая может принимать определённые числовые значения в зависимости от исхода опыта. (например, число глаголов в отрывке данного произведения определённого объёма) Дискретная случайная величина (ДСВ) может принимать только отделённые друг от друга значения (их конечное или счётное число). Непрерывная случайная величина (НСВ) может принимать все значения из некоторого числового промежутка.

ОСНОВНЫЕ ПОНЯТИЯ Закон распределения СВ – соответствие между возможными значениями СВ и их вероятностями. … Для ДСВ – закон распределения Х можно представить в виде таблицы : … где Многоугольник распределения – ломаная линия, последовательно соединяющая точки с координатами … …

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СВ (ИНТЕГРАЛЬНАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ) равна вероятности того, что случайная величина Х примет значение меньшее, чем (где ) Свойства: 1. F(x) – неубывающая; 2. 3. 4. - т. к это вероятность; ;

ФУНКЦИЯ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТИ НСВ (ДИФФЕРЕНЦИАЛЬНАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ) Плотностью вероятности называется первая производная от функции распределения Свойства: 1. , т. к. F(x) – неубывающая; 2. 3. Площадь фигуры под графиком плотности вероятности равна 1.

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СВ Математическое ожидание - это среднее, наиболее ожидаемое значение СВ. Для ДСВ Свойства 1. 2. 3. :

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СВ Дисперсия - математическое ожидание квадрата отклонения значений СВ от её математического ожидания. Для ДСВ находится по формуле: или Свойства : 1). 3). Среднее квадратическое отклонение 2).

ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ДСВ Биномиальный Случайная величина Х распределена по биномиальному закону, если она может принимать значения 0, 1, 2, …, n с вероятностями, которые находятся по формуле Бернулли: ( )

ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ДСВ Закон Пуассона Случайная величина Х распределена по закону Пуассона закону, если она может принимать значения 0, 1, 2, …, n с вероятностями, которые находятся по формуле Пуассона:

ЗАКОНЫ РАСПРЕДЕЛЕНИЯ НСВ Нормальное распределение (закон Гаусса) НСВ Х распределена по нормальному закону Х~N(a; σ), если её функция плотности распределения имеет вид:

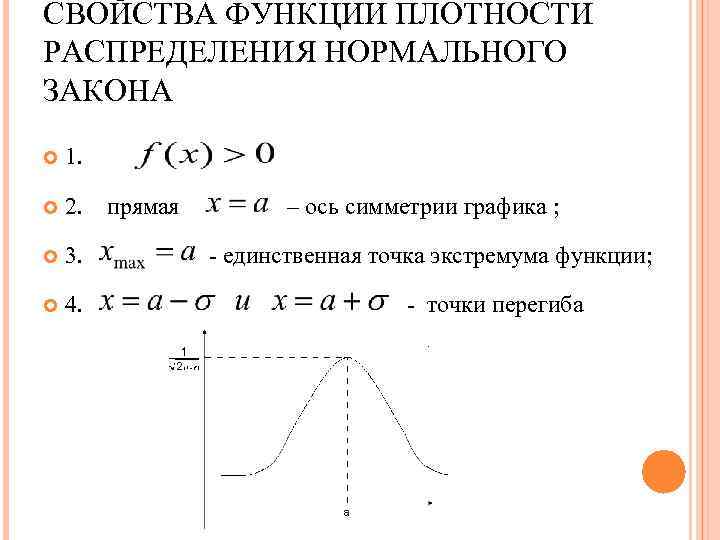СВОЙСТВА ФУНКЦИИ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ НОРМАЛЬНОГО ЗАКОНА 1. 2. 3. 4. прямая – ось симметрии графика ; - единственная точка экстремума функции; - точки перегиба

ЛОГНОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ Значение случайной лингвистической величины Х обычно складывается из независимых внутриязыковых величин. В этом случае нормально распределена не сама СВХ, а её логарифм. Функция плотности логнормального распределения имеет вид: где

ВЕРОЯТНОСТЬ ПОПАДАНИЯ НСВ В ЗАДАННЫЙ ПРОМЕЖУТОК или Если НСВ Х распределена по нормальному закону то где - функция Лапласа

СИСТЕМА ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН (ДВУМЕРНАЯ СВ) Упорядоченная пара (Х ; Y) случайных величин Х и Y называется системой двух СВ или двумерной СВ. Закон распределения двумерной СВ – соответствие между значениями (Х ; Y) и их вероятностями. СВ Х и Y называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. Две СВ Х и Y называются функционально зависимыми, если зная значение одной из них, можно точно указать значение другой. СВ Х и Y связаны стохастической зависимостью, если зная значение одной из них, можно указать закон распределения, а не точное значение другой.

ОПЕРАЦИИ НАД НЕЗАВИСИМЫМИ СЛУЧАЙНЫМИ ВЕЛИЧИНАМИ умножение на число – значения случайных величин умножаются на это число, а их вероятности не изменяются; возведение в натуральную степень – значения возводятся в степень, а вероятности не изменяются; сложение, вычитание, умножение – значения попарно складываются, а соответствующие вероятности перемножаются;

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СИСТЕМЫ ДВУХ СВ Ковариация cov(X, Y) или корреляционный момент математическое ожидание произведения отклонений этих СВ от их математических ожиданий. Коэффициент корреляции где и - средние квадратические отклонения X и Y

СВОЙСТВА КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ: коэффициент корреляции по абсолютной величине не превосходит 1: -1< <1; если Х и Y независимы, то если Х и Y связаны линейной зависимостью, т. е. Х= а Y + в, Причём где а ≠ 0, то если = 1 или = 1 при а > 0 и =0; = 1 или = -1 при а < 0 ; = -1, то Х и Y связаны линейной зависимостью. = -1,