Скачать презентацию СЛУЧАЙНЫЕ ВЕЛИЧИНЫ лекция 3 Постникова Ольга Алексеевна Скачать презентацию СЛУЧАЙНЫЕ ВЕЛИЧИНЫ лекция 3 Постникова Ольга Алексеевна

33011fed_l4_dsv.ppt

  • Количество слайдов: 41

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ лекция № 3 Постникова Ольга Алексеевна 1 СЛУЧАЙНЫЕ ВЕЛИЧИНЫ лекция № 3 Постникова Ольга Алексеевна 1

Тема. Дискретные случайные величины (ДСВ) лекция № 3 Постникова Ольга Алексеевна 2 Тема. Дискретные случайные величины (ДСВ) лекция № 3 Постникова Ольга Алексеевна 2

План: 1. Виды случайных величин. 2. Распределение дискретной случайной величины. 3. Функция распределения. 4. План: 1. Виды случайных величин. 2. Распределение дискретной случайной величины. 3. Функция распределения. 4. Числовые характеристики дискретных случайных величин. лекция № 3 Постникова Ольга Алексеевна 3

1. Виды случайных величин Одним из важнейших понятий в теории вероятностей является понятие случайной 1. Виды случайных величин Одним из важнейших понятий в теории вероятностей является понятие случайной величины. Величина называется случайной, если в результате опыта она может принимать любые заранее неизвестные значения. лекция № 3 Постникова Ольга Алексеевна 4

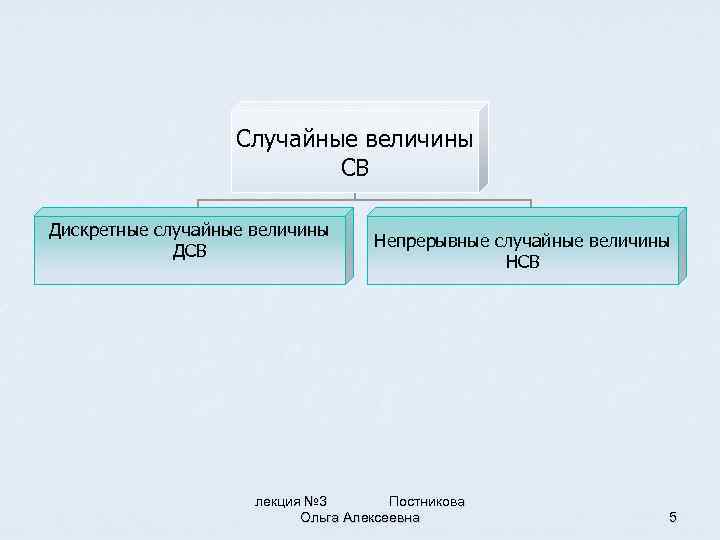Случайные величины CВ Дискретные случайные величины ДСВ Непрерывные случайные величины НСВ лекция № 3 Случайные величины CВ Дискретные случайные величины ДСВ Непрерывные случайные величины НСВ лекция № 3 Постникова Ольга Алексеевна 5

Дискретная случайная величина (ДСВ) – это случайная величина, которая принимает отдельное изолированное, счетное множество Дискретная случайная величина (ДСВ) – это случайная величина, которая принимает отдельное изолированное, счетное множество значений. Пример. Число посетителей поликлиники в течение дня. лекция № 3 Постникова Ольга Алексеевна 6

Непрерывная случайная величина (НСВ) – это случайная величина, принимающая любые значения из некоторого промежутка. Непрерывная случайная величина (НСВ) – это случайная величина, принимающая любые значения из некоторого промежутка. Пример. Масса наугад выбранной таблетки некоторого препарата является НСВ. лекция № 3 Постникова Ольга Алексеевна 7

Случайные величины обозначают заглавными буквами латинского алфавита: X, Y, Z и т. д. , Случайные величины обозначают заглавными буквами латинского алфавита: X, Y, Z и т. д. , а их значения – соответствующими строчными буквами: x, y, z и т. д. лекция № 3 Постникова Ольга Алексеевна 8

Пример. Если случайная величина X имеет три возможных значения, то они могут быть обозначены Пример. Если случайная величина X имеет три возможных значения, то они могут быть обозначены так: x 1, x 2, x 3. X: x 1, x 2, x 3. лекция № 3 Постникова Ольга Алексеевна 9

2. Распределение дискретной случайной величины Законом распределения ДСВ называют соответствие между возможными значениями и 2. Распределение дискретной случайной величины Законом распределения ДСВ называют соответствие между возможными значениями и их вероятностями. Закон распределения можно представить в виде таблицы, формулы, графически. лекция № 3 Постникова Ольга Алексеевна 10

При табличном задании закона распределения ДСВ первая строка таблицы содержит возможные значения, а вторая При табличном задании закона распределения ДСВ первая строка таблицы содержит возможные значения, а вторая – их вероятности: X x 1 x 2 … xn P p 1 p 2 … pn лекция № 3 Постникова Ольга Алексеевна 11

Приняв во внимание, что в одном испытании СВ принимает одно и только одно возможное Приняв во внимание, что в одном испытании СВ принимает одно и только одно возможное значение, получаем, что события X=x 1 , X=x 2 , …, X=xn образуют полную группу, следовательно сумма вероятностей этих событий, то есть сумма вероятностей второй строки таблицы, равна единице: p 1+p 2+…+pn=1. лекция № 3 Постникова Ольга Алексеевна 12

Пример: Вероятности того, что студент сдаст семестровый экзамен в сессию по дисциплинам А и Пример: Вероятности того, что студент сдаст семестровый экзамен в сессию по дисциплинам А и Б соответственно 0, 7 и 0, 9. Составить закон распределения числа семестровых экзаменов, которые сдаст студент. лекция № 3 Постникова Ольга Алексеевна 13

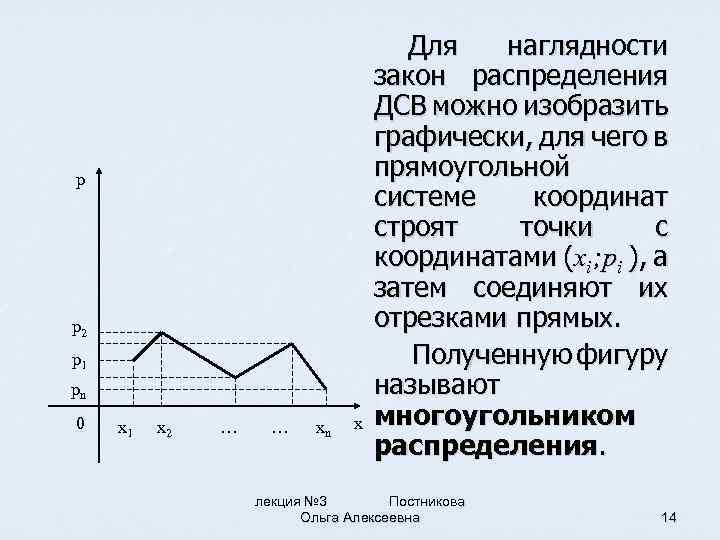p p 2 p 1 pn 0 x 1 x 2 … … xn p p 2 p 1 pn 0 x 1 x 2 … … xn x Для наглядности закон распределения ДСВ можно изобразить графически, для чего в прямоугольной системе координат строят точки с координатами (xi ; pi ), а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения. лекция № 3 Постникова Ольга Алексеевна 14

3. Функция распределения Функцией распределения случайной величины X называется функция действительной переменной x, определяемая 3. Функция распределения Функцией распределения случайной величины X называется функция действительной переменной x, определяемая равенством F(x)=P(X

Так как до значения x 1 случайная величина X не встречалась, то и вероятность Так как до значения x 1 случайная величина X не встречалась, то и вероятность события X< x 1 равна нулю. Для всех значений x 1x 2 СВ уже может принимать два возможных значения x 1 и x 2 , поэтому вероятность события X

Если дискретные значения случайной величины x 1, x 2 , … , xn расположены Если дискретные значения случайной величины x 1, x 2 , … , xn расположены в порядке возрастания, то каждому значению xi этих величин ставится в соответствие сумма вероятностей всех предыдущих значений и вероятности pi: x 1 x 2 x 3 … xn p 1+ p 2 + p 3 … p 1+ p 2 + p 3+ … + pn лекция № 3 Постникова Ольга Алексеевна 17

Нанося на график возможные значения ДСВ X и соответствующие суммы вероятностей, получаем ступенчатую фигуру, Нанося на график возможные значения ДСВ X и соответствующие суммы вероятностей, получаем ступенчатую фигуру, которая и является графиком функции распределения вероятностей. лекция № 3 Постникова Ольга Алексеевна 18

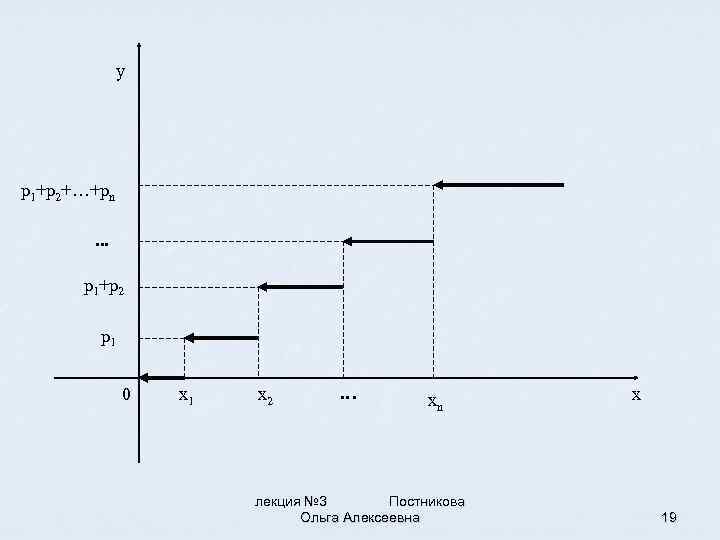y p 1+p 2+…+pn. . . p 1+p 2 p 1 0 x 1 y p 1+p 2+…+pn. . . p 1+p 2 p 1 0 x 1 x 2 … xn лекция № 3 Постникова Ольга Алексеевна x 19

Свойства функции распределения случайной величины X лекция № 3 Постникова Ольга Алексеевна 20 Свойства функции распределения случайной величины X лекция № 3 Постникова Ольга Алексеевна 20

4. Числовые характеристики дискретных случайных величин лекция № 3 Постникова Ольга Алексеевна 21 4. Числовые характеристики дискретных случайных величин лекция № 3 Постникова Ольга Алексеевна 21

1). Математическое ожидание и его свойства Математическим ожиданием ДСВ X называется сумма произведений всех 1). Математическое ожидание и его свойства Математическим ожиданием ДСВ X называется сумма произведений всех ее значений на соответствующие вероятности. лекция № 3 Постникова Ольга Алексеевна 22

Вероятностный смысл математического ожидания: Математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины. Вероятностный смысл математического ожидания: Математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины. (На числовой оси возможные значения расположены слева и справа от математического ожидания, т. е. математическое ожидание больше наименьшего и меньше наибольшего возможных значений). лекция № 3 Постникова Ольга Алексеевна 23

ПРИМЕР Математическое ожидание Если за каждый выпавший орел мы получаем 150 рублей, а при ПРИМЕР Математическое ожидание Если за каждый выпавший орел мы получаем 150 рублей, а при решке — сами отдаем 70 рублей, сколько денег мы в среднем выигрываем на каждом броске? лекция № 3 Постникова Ольга Алексеевна 24

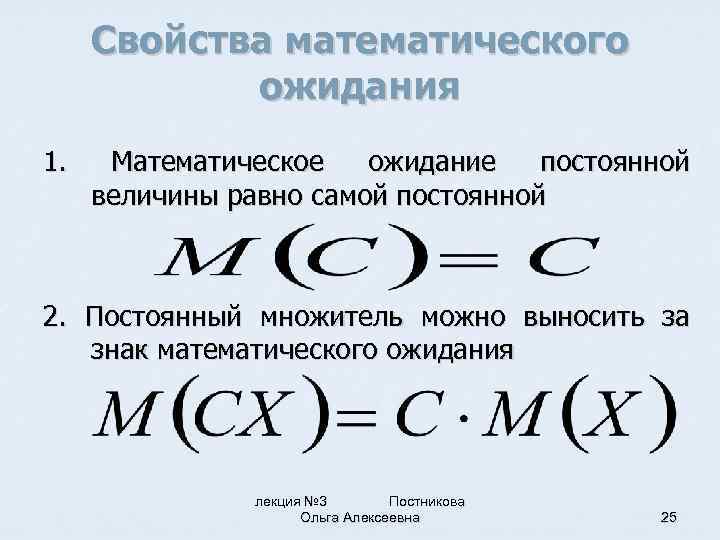Свойства математического ожидания 1. Математическое ожидание постоянной величины равно самой постоянной 2. Постоянный множитель Свойства математического ожидания 1. Математическое ожидание постоянной величины равно самой постоянной 2. Постоянный множитель можно выносить за знак математического ожидания лекция № 3 Постникова Ольга Алексеевна 25

3. Математическое ожидание суммы конечного числа случайных величин равно сумме их математических ожиданий лекция 3. Математическое ожидание суммы конечного числа случайных величин равно сумме их математических ожиданий лекция № 3 Постникова Ольга Алексеевна 26

4. Математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий. 4. Математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий. (Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина) лекция № 3 Постникова Ольга Алексеевна 27

2). Дисперсия и ее свойства Дисперсией (рассеянием) ДСВ называется математическое ожидание квадрата отклонения СВ 2). Дисперсия и ее свойства Дисперсией (рассеянием) ДСВ называется математическое ожидание квадрата отклонения СВ от ее математического ожидания лекция № 3 Постникова Ольга Алексеевна 28

Свойства дисперсии: 1. Дисперсия постоянной величины равна нулю лекция № 3 Постникова Ольга Алексеевна Свойства дисперсии: 1. Дисперсия постоянной величины равна нулю лекция № 3 Постникова Ольга Алексеевна 29

2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат лекция № 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат лекция № 3 Постникова Ольга Алексеевна 30

3. Дисперсия суммы конечного числа независимых СВ равна сумме их дисперсий лекция № 3 3. Дисперсия суммы конечного числа независимых СВ равна сумме их дисперсий лекция № 3 Постникова Ольга Алексеевна 31

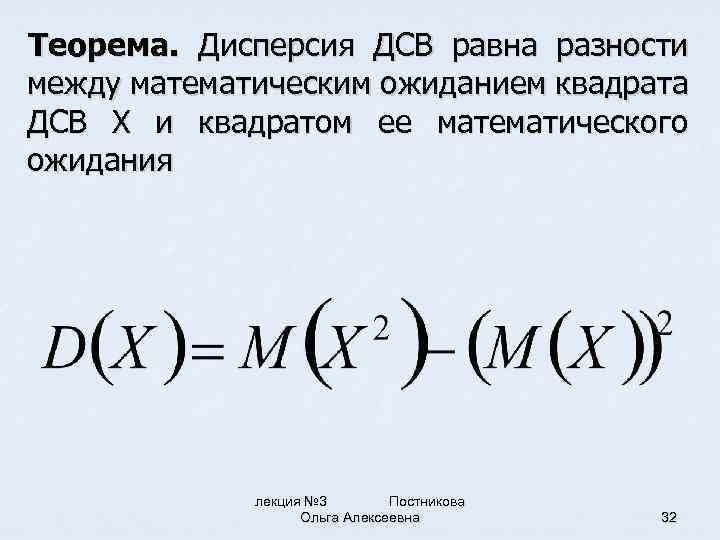Теорема. Дисперсия ДСВ равна разности между математическим ожиданием квадрата ДСВ X и квадратом ее Теорема. Дисперсия ДСВ равна разности между математическим ожиданием квадрата ДСВ X и квадратом ее математического ожидания лекция № 3 Постникова Ольга Алексеевна 32

3). Среднее квадратическое отклонение Средним квадратическим отклонением случайной величины X называется арифметическое значение корня 3). Среднее квадратическое отклонение Средним квадратическим отклонением случайной величины X называется арифметическое значение корня квадратного из ее дисперсии лекция № 3 Постникова Ольга Алексеевна 33

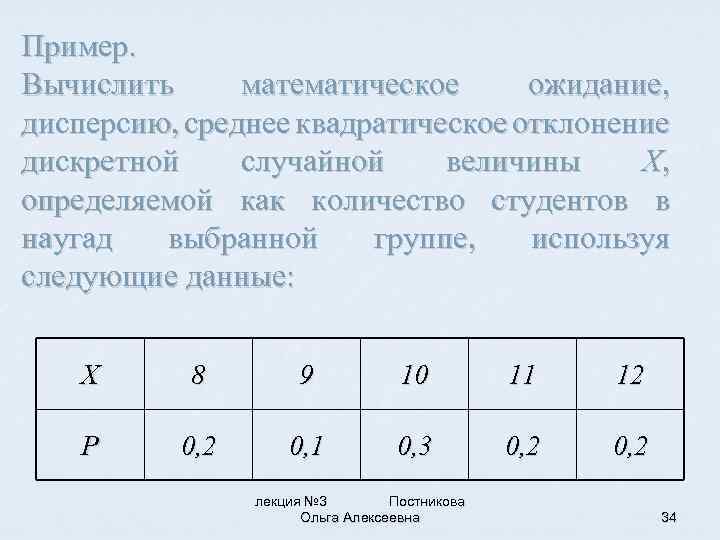Пример. Вычислить математическое ожидание, дисперсию, среднее квадратическое отклонение дискретной случайной величины X, определяемой как Пример. Вычислить математическое ожидание, дисперсию, среднее квадратическое отклонение дискретной случайной величины X, определяемой как количество студентов в наугад выбранной группе, используя следующие данные: X 8 9 10 11 12 P 0, 2 0, 1 0, 3 0, 2 лекция № 3 Постникова Ольга Алексеевна 34

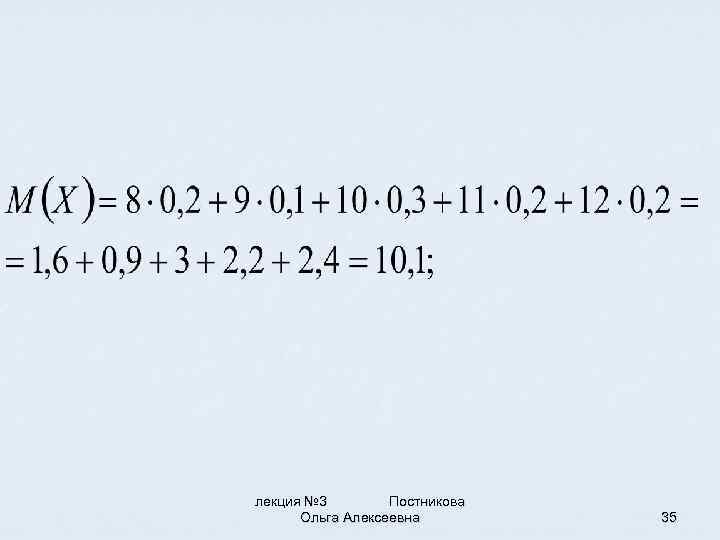лекция № 3 Постникова Ольга Алексеевна 35 лекция № 3 Постникова Ольга Алексеевна 35

лекция № 3 Постникова Ольга Алексеевна 36 лекция № 3 Постникова Ольга Алексеевна 36

Замечание. Математическое ожидание и дисперсия числа появлений события в независимых испытаниях Если вероятность появления Замечание. Математическое ожидание и дисперсия числа появлений события в независимых испытаниях Если вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания являются независимыми. Пусть эти вероятности одинаковы и равны p. Тогда вероятность не наступления события А в испытании лекция № 3 q=1 -p. Постникова Ольга Алексеевна 37

Теорема. Математическое ожидание числа появлений события А в независимых испытаниях равно произведению числа испытаний Теорема. Математическое ожидание числа появлений события А в независимых испытаниях равно произведению числа испытаний на вероятность появления события А в каждом испытании: лекция № 3 Постникова Ольга Алексеевна 38

Теорема. Дисперсия числа появлений события А в независимых испытаниях равна произведению числа испытаний на Теорема. Дисперсия числа появлений события А в независимых испытаниях равна произведению числа испытаний на вероятности появления и не появления события А в одном испытании: лекция № 3 Постникова Ольга Алексеевна 39

Пример. В пяти аптеках проверяется годовой баланс. Вероятность правильного оформления баланса в каждой аптеке Пример. В пяти аптеках проверяется годовой баланс. Вероятность правильного оформления баланса в каждой аптеке равна 0, 7. Найти математическое ожидание и дисперсию правильно оформленных балансов. Решение. По условию n=5; p=0, 7; q=1 -0, 7=0, 3. лекция № 3 Постникова Ольга Алексеевна 40

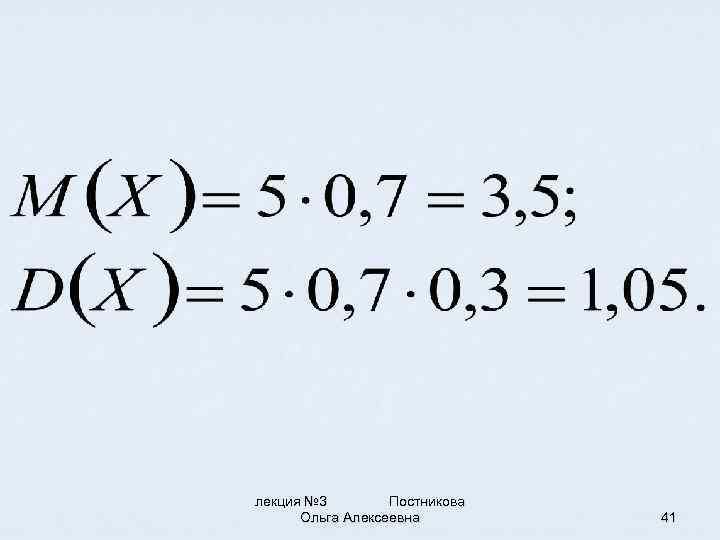лекция № 3 Постникова Ольга Алексеевна 41 лекция № 3 Постникова Ольга Алексеевна 41