Случайные величины и их числовые характеристики Понятие

Случайные величины и их числовые характеристики

Понятие случайной величины Величина называется случайной, если в результате испытания она принимает лишь одно из возможных значений, зависящее от случайных причин. n Обозначение: Х, Y, Z… n Примеры: n ¨ Число очков, выпавших на игральной кости; ¨ Число бракованных изделий в партии; ¨ Число детей, родившихся в течение суток; ¨ Дальность полета артиллерийского снаряда; ¨ Наружный диаметр трубы

Понятие случайной величины n Наиболее полным, исчерпывающим описанием случайной величины является закон ее распределения. n Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями СВ и соответствующими им вероятностями.

Виды случайных величин Случайная величина называется дискретной (прерывной), если множество ее значений конечно или счётно (т. е. их можно занумеровать натуральными числами). n Непрерывной называют случайную величину, множество значений которой есть интервал числовой оси (бесконечное несчётное множество). n

Способы задания ДСВ n Таблицей – рядом распределения n Формулой: Графически – многоугольником или полигоном распределения вероятностей n

Задача 1 n n n Партия из 8 изделий содержит 5 стандартных. Наудачу отбираются 3 изделия. Составить закон распределения числа стандартных изделий среди отобранных. Пусть Х - число стандартных деталей в выборке. Х может принимать 4 возможных значения: 0, 1, 2 и 3. Вероятность нахождения k стандартных изделий среди трех отобранных определяется формулой

Задача 1 n Варьируя значения k от 0 до 3, вычисляем вероятности: Проверка: n Строим ряд распределения: n

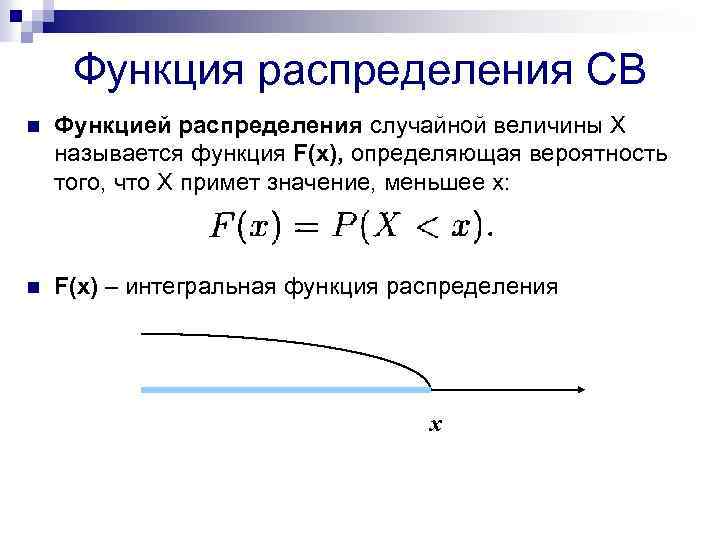Функция распределения СВ n Функцией распределения случайной величины Х называется функция F(x), определяющая вероятность того, что Х примет значение, меньшее х: n F(x) – интегральная функция распределения х

Свойства F(x) n Область значений F(x) - отрезок [0, 1]: n F(x) – неубывающая функция. Если множество значений СВ - интервал (а, b), то ¨ F(x) = 0 при х ≤ а ¨ F(x) = 1 при х ≥ b. Если множество значений СВ - вся числовая ось, то n n Вероятность того, что НСВ примет любое конкретное значение, равна нулю: Вероятность того, что НСВ примет значения из интервала (α, β), равна:

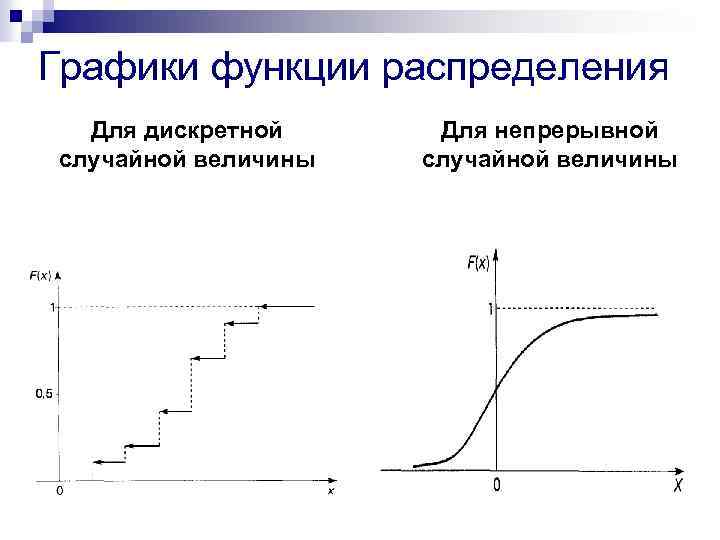Графики функции распределения Для дискретной случайной величины Для непрерывной случайной величины

Виды случайных величин По виду функции F(x) определяется и вид случайной величины: n Случайная величина называется непрерывной, если ее функция распределения непрерывна и дифференцируема всюду, кроме, может быть, отдельных точек. n Дискретной называют случайную величину с кусочнонепрерывной функцией распределения.

Плотность распределения вероятностей n Первая производная от функции распределения F(x) непрерывной случайной величины X называется плотностью распределения вероятностей и обозначается f(x): n f(x) – дифференциальная функция распределения Плотность распределения — это "скорость" изменения вероятности Р(Х < х). График плотности вероятности f(x) называется кривой распределения n n

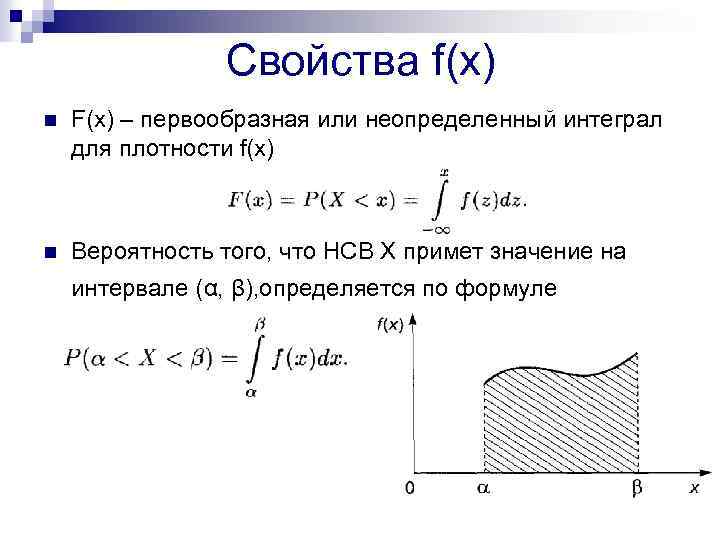Свойства f(x) n F(x) – первообразная или неопределенный интеграл для плотности f(x) n Вероятность того, что НСВ Х примет значение на интервале (α, β), определяется по формуле

Свойства f(x) n Плотность распределения является неотрицательной функцией: n Интеграл от плотности распределения по всей числовой оси равен единице: n Если множеством значений случайной величины Х является интервал (а, b), то

Задача 2 n Непрерывная случайная величина Х задана плотностью распределения на всей числовой оси n Найти вероятность того, что Х примет значение на интервале (-1, 1). Согласно свойству плотности: n

Числовые характеристики случайных величин

Числовые характеристики СВ Закон распределения полностью описывает дискретную случайную величину. Но часто достаточно знать лишь ее некоторые обобщенные характеристики. К ним относятся n математическое ожидание, n дисперсия, n среднее квадратичное отклонение.

Математическое ожидание n Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных ее значений на их вероятности: где n Математическое ожидание называют также ожидаемым значением случайной величины, средним значением случайной величины.

Свойства математического ожидания

n Случайная величина Х задана рядом распределения. Задача 3 Х 2 5 8 19 Найдите ее математическое ожидание. 0, Р 0, 2 0, 4 0, 1 3

Математическое ожидание n Математическим ожиданием непрерывной случайной величины X, возможные значения которой находятся на отрезке [а, b], называется определенный интеграл: n Если возможные значения случайной величины Х заполняют всю ось Ох,

Дисперсия СВ n Дисперсией или рассеянием случайной величины X называется математическое ожидание квадрата ее отклонения :

Свойства дисперсии

Задача 3 Х 2 5 8 19 Случайная величина Х Р 0, 2 0, 3 0, 4 0, 1 задана рядом распределения. Найдите ее дисперсию. n 1 способ – по определению: n По задаче 2 n Построим ряд распределения для квадрата отклонения (Х-МХ)2 (2 -7)2=25 (5 -7)2=4 (8 -7)2=1 (19 -7)2=12 n Р 0, 2 0, 3 0, 4 0, 1

Задача 3 n n 2 способ – по формуле Построим ряд распределения Х 2: 2 n 4 25 64 361 Р n Х 0, 2 0, 3 0, 4 0, 1 По задаче 2 Вычислим дисперсию по формуле:

Дисперсия n Дисперсией непрерывной случайной величины Х называется математическое ожидание квадрата ее отклонения: n Для НСВ Х, определенной на интервале (a, b): n Для вычисления дисперсии используют также формулу:

Среднее квадратичное отклонение СВ n Средним квадратичным отклонением или стандартом случайной величины называется арифметическое значение квадратного корня из ее дисперсии: n Стандарт является характеристикой рассеяния СВ

Основные законы распределения случайных величин

Биномиальное распределение n n n Проведем n опытов. Рассмотрим событие A, которое происходит в каждом опыте с вероятностью p. Число успехов в этой серии опытов и есть значение случайной величины X. Случайная величина называется распределенной по биномиальному закону с параметрами n и p, если может принимать лишь значения 0, 1, …, n c вероятностями , где Числовые характеристики:

Распределение Пуассона n Случайная величина Х имеет закон распределения Пуассона (закон редких явлений) с параметром λ>0, если она принимает значения 0, 1, 2, …, m, … (бесконечное, но счётное множество значений) с вероятностями n Числовые характеристики:

Равномерное распределение n НСВ имеет равномерный закон распределения на промежутке (а, b), если ее плотность вероятности постоянна на этом промежутке и равна нулю вне его: n n Числа а и b - параметры равномерного распределения Числовые характеристики n Вероятность попадания значения Х в интервал (α, β)

Нормальное распределение n Непрерывная случайная величина имеет нормальный закон распределения (закон Гаусса) с параметрами а и σ, если ее плотность вероятности имеет вид n Нормальный закон распределения с параметрами а и σ обозначается n Числовые характеристики:

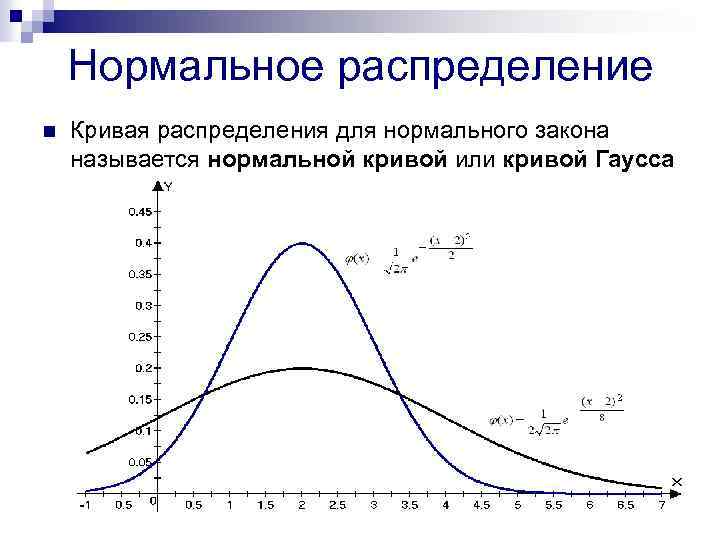Нормальное распределение n Кривая распределения для нормального закона называется нормальной кривой или кривой Гаусса

Нормальное распределение n Нормальное распределение с параметрами а = 0 и σ = 1 называется нормированным, стандартным или гауссовым; его плотность равна функции Гаусса: n Функция распределения в случае стандартного нормального распределения совпадает с функцией Лапласа:

Нормальное распределение n Вероятность попадания случайной величины Х, распределенной по нормальному закону, в интервал равна для гауссова распределения: n Вероятность отклонения случайной величины Х, распределенной по нормальному закону, от ее среднего значения а на величину, не превышающую ε, равна

Правило трёх сигм n Используя табличные значения функции Лапласа, найдем вероятность n Эту особенность нормального распределения называют «правилом трех сигм» . n «Правило трех сигм» : Если случайная величина имеет нормальный закон распределения с параметрами а и σ, то практически достоверно, что ее значения заключены в интервале