Случайной величиной называется величина, которая в результате опыта

Случайной величиной называется величина, которая в результате опыта принимает заранее неизвестное численное значение. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Т.е. значения, которые она может принимать в результате опыта, образуют множество ее возможных значений или спектр значений. Случайные величины бывают непрерывными и дискретными. Будем обозначать случайные величины Х, а их возможные значения х. Например, пусть Х - число очков, выпавших при бросании кубика. Х - случайная величина и множество ее значений будет: {1,2,3,4,5,6}

Случайная величина называется дискретной, если множество ее возможных значений cчетно (т.е. все возможные значения можно пронумеровать натуральными числами) {x1 ,x2 ,…,xn }

Дискретная случайная величина полностью определяется своим рядом распределения. Ряд распределения представляет собой таблицу, в которой указаны все возможные значения случайной величины и их вероятности:

Поскольку ряд распределения содержит все возможные значения случайной величины, то суммарная вероятность должна быть равна 1. По ряду распределения можно находить различные вероятности и строить многоугольник распределения. Многоугольник распределения – ломаная, которая соединяет точки, абсциссы которых содержит первая строка ряда распределения (значения случайной величины), а ординаты – вторая строка (вероятности этих значений).

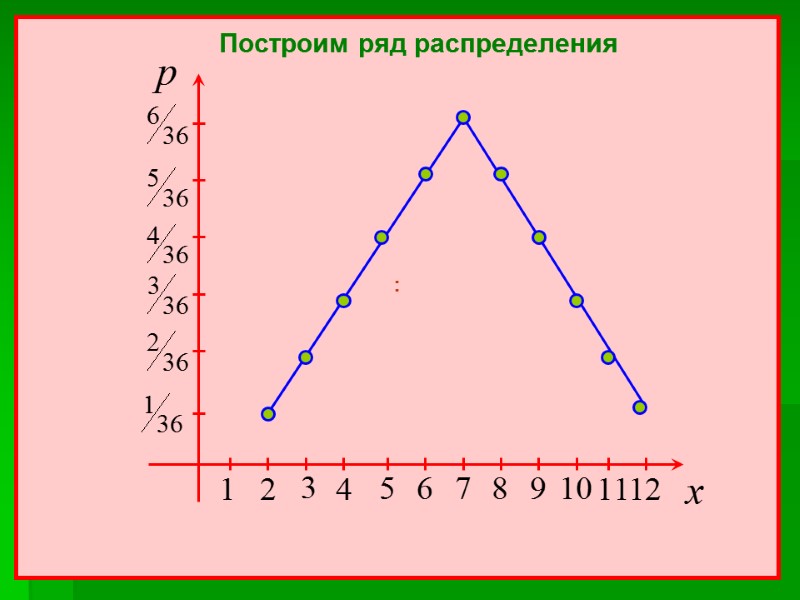
ПРИМЕР Рассмотрим опыт с бросанием двух игральных кубиков. Пусть случайная величина Х - сумма выпавших очков. Составим для нее ряд распределения: Найдем вероятность следующих событий: Р(X<5), P(X>10), P(3

Р(X<5)=P(X=2)+P(X=3)+P(X=4)= =1/36+2/36+3/36=6/36=1/6 Р(X>10)=P(X=11)+P(X=12)= =2/36+1/36=3/36=1/12 P(3

: Построим ряд распределения

МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ И ЕГО СВОЙСТВА Пусть Х - дискретная случайная величина, заданная своим рядом распределения:

Математическим ожиданием M[X] случайной величины Х называется сумма ряда

Например, в рассмотренном выше примере с двумя игральными кубиками:

Среднее арифметическое значений, принимаемых случайной величиной в длинной серии опытов, приближенно равно ее математическому ожиданию. ТЕОРЕМА

Найдем среднее арифметическое этой случайной величины: Эта теорема выражает приближенную связь между средним арифметическим и математическим ожиданием. ДОКАЗАТЕЛЬСТВО: Проведем n опытов. Пусть при этом случайная величина Х приняла значение х1 - n1 раз, х2 - n2 раз ... хm - nm раз. =

Так как отношение вида ni/n определяет частоту события в данной серии опытов, то при достаточно большом числе опытов оно приближается к вероятности этого события: =

Математическое ожидание от постоянной величины равно этой постоянной величине: М[C]=C, C=const 1 СВОЙСТВА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ

Рассмотрим ряд распределения случайной величины Х=С: Тогда математическое ожидание будет равно М[C]=C Доказательство:

Математическое ожидание суммы случайных величин Х и У равно сумме математических ожиданий этих величин: М[X+Y]=M[X]+M[Y] 2

Перегруппируем слагаемые иначе: Распишем математическое ожидание суммы двух случайных величин по определению: Доказательство: = = =

Каждую сумму разобьем на две (по a и b соответственно): Вторые суммы в каждом из слагаемых дают, соответственно, Р(Х=а) и Р(Х=b) и по определению математического ожидания имеем: = = =

Математическое ожидание суммы случайной величины Х и постоянной величины С равно сумме математического ожидания Х и самой величины С: М[X+С]=M[X]+С 3

Используем второе свойство математического ожидания: М[X+С]=M[X]+М[С] На основании первого свойства: М[С]=С Тогда М[X+С]=M[X]+С Доказательство:

Постоянную величину можно выносить за знак математического ожидания: М[k X]=k M[X], где k=cоnst. 4

Постоянную k можно вынести за знак суммы: Используем определение мат. ожидания: Доказательство: = =

Математическое ожидание произведения независимых случайных величин Х и У равно произведению математических ожиданий этих величин: М[XY]=M[X]M[Y] 5

Для независимых случайных величин: Распишем математическое ожидание по определению: Доказательство: = Тогда: =

ДИСПЕРСИЯ И ЕЕ СВОЙСТВА Дисперсия - это мера рассеяния значений случайной величины около ее математического ожидания:

Найдем математическое ожидание и дисперсию этой случайной величины. Например, пусть случайная величина Х задана рядом распределения:

Для вычисления дисперсии часто используют другую формулу:

Доказательство: Используем свойства математического ожидания:

СВОЙСТВА ДИСПЕРСИИ Дисперсия от постоянной величины равна нулю: D[C]=0, C=const 1

Доказательство: Используем второе выражение для дисперсии. Так как M[C]=C, M[C2]=C2 то D[C]=M[C2]-(M[C])2=C2-C2=0

Дисперсия суммы случайной величины Х и постоянной величины С равна дисперсии величины Х : D[X+С]=D[X] 2

Доказательство: По свойству математического ожидания: М[X+С]=M[X]+С Поэтому на основании определения дисперсии:

Постоянная величина выносится за знак дисперсии в квадрате: D[k X]=k2 D[X] 3

Доказательство: По свойству математического ожидания: Используем определение дисперсии:

4 Дисперсия всегда неотрицательна:

5 Дисперсия суммы двух случайных величин находится по формуле:

Величина KXY называется корреляционным моментом случайных величин X и Y: Корреляционный момент описывает взаимодействие двух случайных величин. Если случайные величины X и Y независимы, то их корреляционный момент равен 0.

Математическое ожидание суммы равно сумме математических ожиданий: Распишем дисперсию суммы случайных величин по определению дисперсии: Доказательство:

Перегруппируем слагаемые: Снова используем свойства математического ожидания: Под знаком математического ожидания раскрываем квадрат суммы:

Квадратный корень из дисперсии называется средним квадратичным отклонением: Дисперсия имеет размерность квадрата случайной величины, а среднее квадратичное отклонение имеет размерность самой случайной величины.