СЛОЖНЫЙ ТЕПЛООБМЕН.ppt
- Количество слайдов: 19

СЛОЖНЫЙ ТЕПЛООБМЕН Виды сложного теплообмена

Сложным теплообменом называется процесс переноса теплоты излучением, теплопроводностью и конвекцией. В связи с тем, что в сложном теплообмене главную роль играет радиационный теплообмен, то различают радиационно – кондуктивный и радиационно-конвективный виды теплообмена. Радиационно – кондуктивный теплообмен представляет собой процесс теплообмена, в котором имеют место только теплопроводность и излучение. Радиационно-конвективный теплообмен представляет собой процесс теплообмена, в котором имеют место только конвекция и излучение. Полная система уравнений сложного теплообмена в большинстве случаев не может быть решена аналитически. Поэтому в инженерной практике используют принцип независимости видов теплообмена друг от друга.

Радиационно – кондуктивный теплообмен Этот вид теплообмена является достаточно распространенным в технике. В качестве примера можно назвать теплопотери через стенки сосуда Дьюара. В наиболее простых случаях предполагают, что эти виды теплообмена не взаимодействуют друг с другом по отношению к искомой величине. Поэтому они рассматриваются отдельно, а полученные результаты суммируются. В этих задачах можно использовать все ранее изложенные методы расчета теплообмена излучением и теплопроводностью без изменений. Рассмотрим две параллельные бесконечные черные пластины, разделенные прозрачной для теплового излучения средой толщиной b с коэффициентом теплопроводности λ (рис. ). Температуры пластин обозначим соответственно

Результирующий радиационной тепловой поток складывается из и кондуктивной составляющих и равен потоку энергии и, который необходимо подвести к пластине поддержания постоянства ее температуры: Плотности потока энергии, теплопроводностью, равны: переносимой Тогда плотность результирующего потока: 1 для излучением и

Однако в ряде случаев теплопроводность и излучение взаимодействуют друг с другом. Рассмотрим тот же пример (рис. ), который дополним величиной -поток энергии, отводимый к поверхности 2. Необходимо температуру определить поверхности 1. Преобразуем уравнение энергии к виду: l l Q 2 s. T 1 + T 1 = s. T + T 2 + b b F 4 4 2 Это нелинейное уравнение может быть решено только численным методом. Решение усложняется, если необходимо учесть изменение физических свойств от температуры.
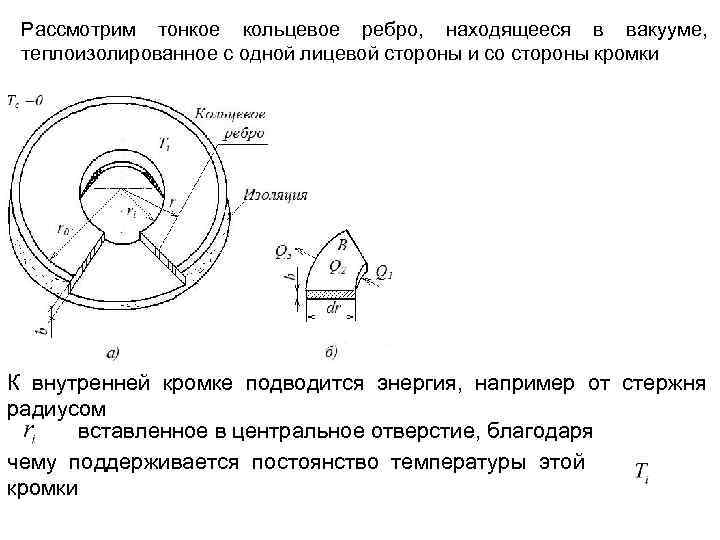
Рассмотрим тонкое кольцевое ребро, находящееся в вакууме, теплоизолированное с одной лицевой стороны и со стороны кромки К внутренней кромке подводится энергия, например от стержня радиусом вставленное в центральное отверстие, благодаря чему поддерживается постоянство температуры этой кромки

Неизолированная кольцевая поверхность является диффузносерой и имеет степень черноты Она излучает энергию в окружающее пространство с температурой На рис. обозначены: подводимый и отводимый тепловые потоки вследствие теплопроводности, – тепловой поток вследствие излучения. Требуется определить распределение температуры по радиусу кольцевого ребра. Если диск считать достаточно тонким, то локальную температуру можно принять постоянной по толщине Тогда баланс энергии для любого кольцевого элемента шириной можно представить в виде:

Если постоянные Для решения этого уравнения запишем граничные условия: – на внутренней кромке при – на внешней кромке при отсутствии теплового потока при Введем безразмерные переменные Перепишем уравнение в новых переменных:

Далее введем вспомогательные параметры – при Решение можно получить численным методом. При использовании охлаждающих ребер применяется понятие эффективности ребра – отношения энергии, действительно рассеиваемой ребром путем излучения, к энергии, которая могла. бы быть рассеяна при постоянстве температуры Для случая на рис.

Если поверхность имеет ряд ребер, то в уравнении энергии появляются интегральные члены. Радиационно-конвективный теплообмен Этот вид теплообмена также является достаточно распространенным в технике. И также как в радиационно – кондуктивном методе, в наиболее простых случаях предполагают, что эти виды теплообмена не взаимодействуют друг с другом по отношению к искомой величине. Поэтому они рассматриваются отдельно, а полученные результаты суммируются: Тогда плотность результирующего потока:
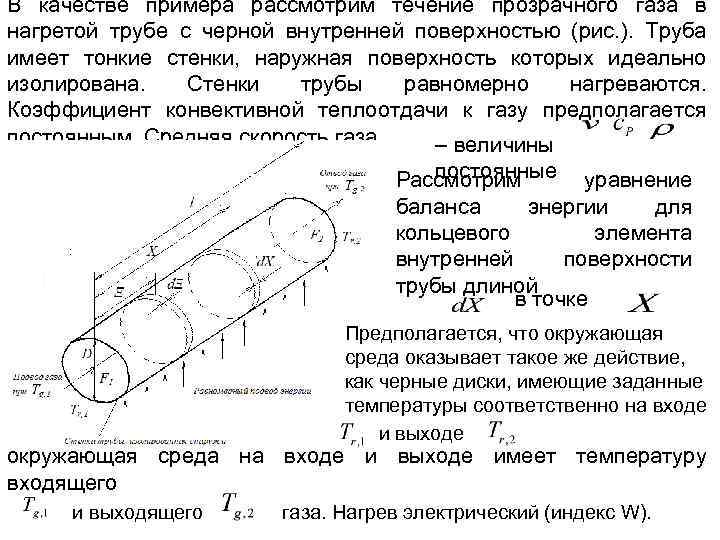
В качестве примера рассмотрим течение прозрачного газа в нагретой трубе с черной внутренней поверхностью (рис. ). Труба имеет тонкие стенки, наружная поверхность которых идеально изолирована. Стенки трубы равномерно нагреваются. Коэффициент конвективной теплоотдачи к газу предполагается постоянным. Средняя скорость газа – величины постоянные уравнение Рассмотрим баланса энергии для кольцевого элемента внутренней поверхности трубы длиной в точке : Предполагается, что окружающая среда оказывает такое же действие, как черные диски, имеющие заданные температуры соответственно на входе и выходе окружающая среда на входе и выходе имеет температуру входящего и выходящего газа. Нагрев электрический (индекс W).

Энергия, отводимая конвекцией и излучением от кольцевого элемента, расположенного на расстоянии от входа, равна: Пренебрегая теплопроводностью в осевом направлении, получим, что поток энергии, подводимой к кольцевому элементу, будет равен потоку энергии, отводимой от него энергии. уравнение баланса энергии: (1)

(2) (3) Таким образом, уравнения (1 -3) образуют систему уравнений с неизвестными: распределение местной температуры стенки по длине трубы

Теплопередача В технических устройствах (камерах сгорания теплогенерирующих устройств, теплообменниках и т. п. ) передача теплоты может осуществляться одновременно всеми видами теплообмена. Аналитических решений таких процессов не существует. Для решения применяются численные методы. В простейшем случае для плоской стенки задачу о теплопередаче можно решать с помощью термического сопротивления теплопередаче: Коэффициенты теплоотдачи и в общем случае состоят из коэффициентов конвективной теплоотдачи излучением

, называется коэффициентом теплопередачи Величина, обратная , Вт/(м 2 ∙К): Для цилиндрической стенки на 1 м длины трубы:

Для плоской оребренной стенки: – отношение площади поверхности с оребрением к площади той же поверхности без оребрения. Учитывая, что для тонких металлических стенок труб величино можно пренебречь, т. к. она существенно меньше сопротивлений теплоотдачи, тогда:

Отсюда плотность теплового потока: Таким образом, коэффициент теплопередачи представляет собой количество теплоты, переносимой от одной жидкой среды к другой через стенку площадью 1 м 2 за 1 с при разности температур в 1°К. Значение Зная всегда меньше любого из коэффициентов и одну из температур можно найти температуру поверхностей любого слоя. многослойной стенки: и т. д.

Для расчета сложного теплообмена применяются критерии (числа) Число характеризует радиационно-конвективный теплообмен. Чем меньше его значение, тем больше роль радиационного теплообмена по сравнению с конвективным. Число Больцмана - характеризует радиационно-кондуктивный теплообмен. Число Кирпичева коэффициент ослабления среды Тепловой аналог Re. обобщенный коэффициент переноса, учитывающий кондуктивный, турбулентный и радиационный перенос теплоты

Энергетический баланс на границе среды с поверхностью тела позволяет получить число Старка – Число является аналогом числа и характеризует связь между температурным полем в твердом теле и радиационным теплообменом на поверхности тела. Уравнение переноса лучистой энергии позволяет получить число Бугера – характерный размер ослабляющей среды; – среднее значение коэффициента ослабления среды. Радиационное число Нуссельта
СЛОЖНЫЙ ТЕПЛООБМЕН.ppt