Сложность арифметических операций с целыми числами Карондеев А

Сложность арифметических операций с целыми числами Карондеев А. М. ИУ 8 -104 1

Сложность алгоритма Элементарные операции Вес элементарных операций Требуемый размер памяти 2

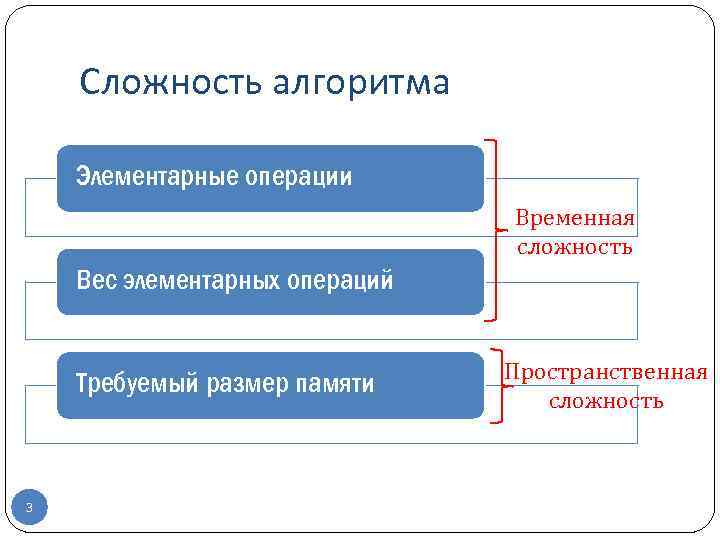Сложность алгоритма Элементарные операции Временная сложность Вес элементарных операций Требуемый размер памяти 3 Пространственная сложность

Алгебраическая сложность алгоритма Определена одна операция Вес операции равен 1 и не зависит от значений операндов Число дополнительных величин заданного типа 4

Битовая сложность алгоритма Битовые операции Вес любой битвой операции 1 Требуемое число дополнительных бит памяти 5

Сложение Битовая сложность • O(n) • Существенно зависит от всех битов входа => асимптотически лучше нельзя 6

Вычитание Битовая сложность • O(n) • Сложение с отрицательный числом 7

Умножение Битовая сложность • Mn = ? 8

Умножение столбиком Битовая сложность • Mn = O(n 2) 9

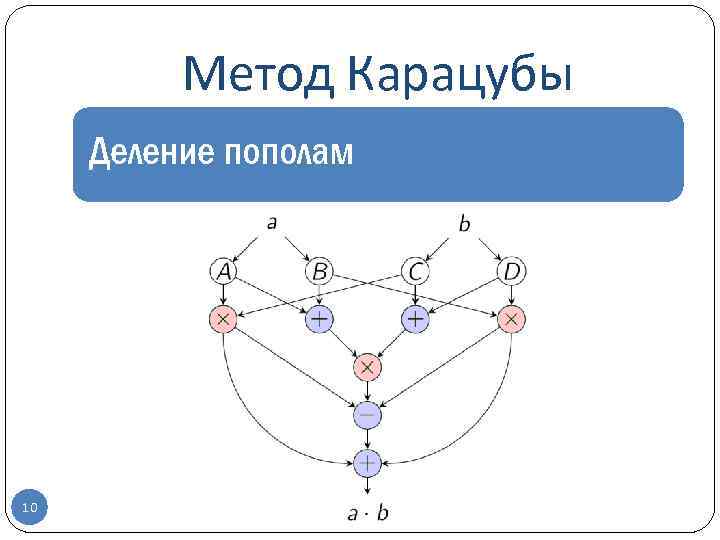Метод Карацубы Деление пополам 10

Метод Карацубы Битовая сложность • Mn = O(nlog 3) = O(n 1. 585) 2 11

Метод Тоома-Кука Битовая сложность • ∀ε > 0 Mn = O(n 1+ε) 12

Метод Шёнхаге-Штрассена 13

Метод Шёнхаге-Штрассена Основная идея • Представление числа как многочлена: 1310 = 11012 = x 3 + x 2 + 1 14

Метод Шёнхаге-Штрассена Основная идея • Представление числа как многочлена • Быстрое преобразование Фурье 15

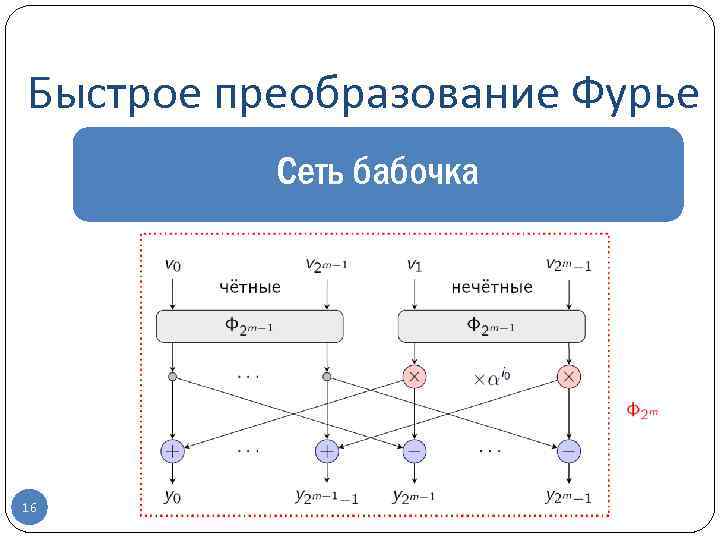Быстрое преобразование Фурье Сеть бабочка 16

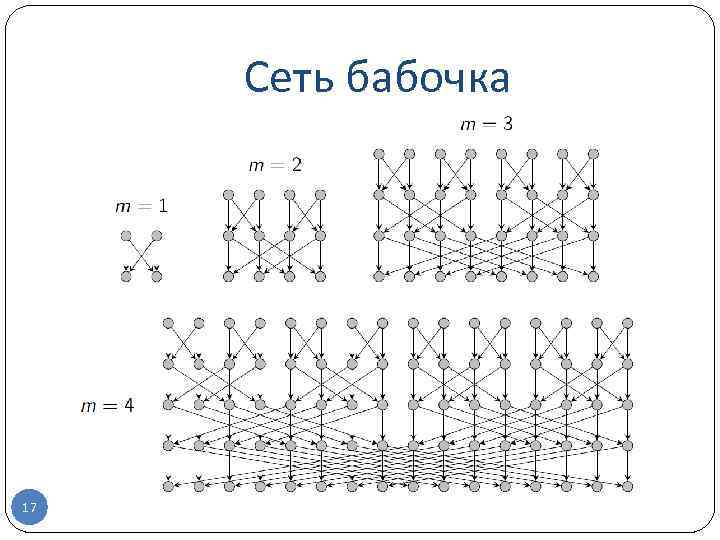Сеть бабочка 17

Метод Шёнхаге-Штрассена Битовая сложность • Mn = O(n·log 2 n) 18

Метод Фюрера Битовая сложность • Mn = O(n·log 2 n· 2 O(log *n)) 2 19

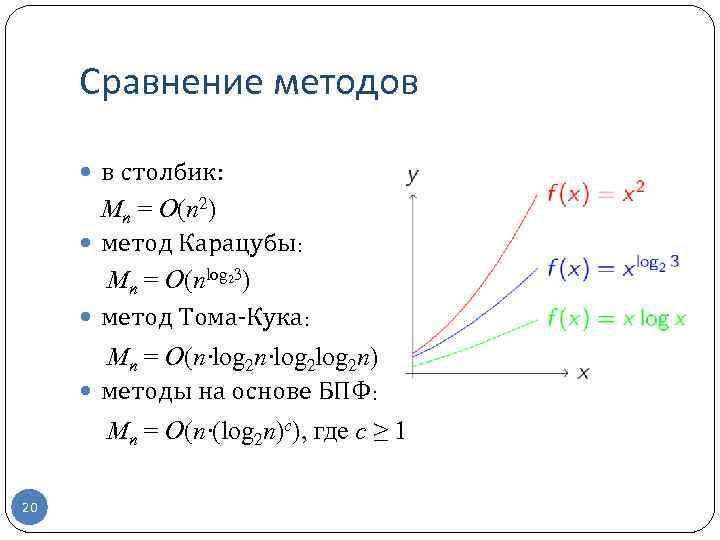Сравнение методов в столбик: Mn = O(n 2) метод Карацубы: Mn = O(nlog 23) метод Тома-Кука: Mn = O(n·log 2 log 2 n) методы на основе БПФ: Mn = O(n·(log 2 n)c), где с ≥ 1 20

Деление Битовая сложность • Сводим к умножению 21

Наибольший общий делитель Алгоритм Эвклида: O((log 2 N)2) Бинарный метод: O((log 2 N)2) 22

Наибольший общий делитель Алгоритм Эвклида: O((log 2 N)2) Бинарный метод: O((log 2 N)2) повышение быстродействия • Алгоритм Лемера 23

Спасибо за внимание 24