Лекция 7. Сложное сопротивление.ppt
- Количество слайдов: 17

Сложное сопротивление • Сложный и косой изгиб • Внецентренное растяжение (сжатие)

Вопросы для самопроверки 1. Какой изгиб называется косым? 2. Может ли балка круглого поперечного сечения испытывать косой изгиб? 3. Сочетанием каких видов изгиба является косой изгиб? 4. По каким формулам определяются нормальные напряжения в поперечных сечениях бруса при косом изгибе? 5. Как определяются перемещения точек оси балки при косом изгибе? 6. Какое сложное сопротивление называется внецентренным растяжением или сжатием?

Вопросы для самопроверки 7. Какой брус называется жестким при внецентренном растяжении или сжатии? 8. Какой брус называется гибким при внецентренном растяжении или сжатии? 9. По каким формулам определяются нормальные напряжения в поперечных сечениях бруса при внецентренном растяжении (сжатии)? 10. Как определяется положение нейтральной оси при внецентренном растяжении (сжатии)? 11. Вывод формулы для определения положения нейтральной оси при внецентренном растяжении (сжатии) 12. Что называется ядром сечения?
Вопросы для самопроверки 13. Как строится ядро сечения? 14. Построить ядро сечения для прямоугольника 15. Построить ядро сечения для круга

Сложное сопротивление Сложным называется изгиб, вызванный силами или моментами, расположенными в двух и более плоскостях, проходящих через ось балки. Эти плоскости могут, как совпадать, так и не совпадать с главными плоскостями инерции Под сложным сопротивлением подразумевают деформации бруса возникающие в результате комбинации, в различных сочетаниях, простых видов деформаций: растяжения (сжатия), среза, кручения и изгиба. В большинстве случаев в опасной точке поперечного сечения бруса касательные напряжения, либо равны нулю, либо весьма малы по сравнению с нормальными напряжениями, поэтому расчеты на прочность ведут с учетом только нормальных напряжений.
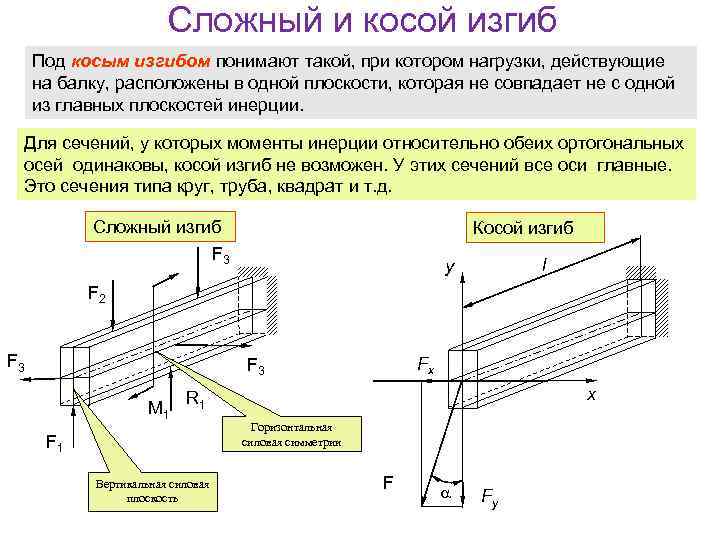
Сложный и косой изгиб Под косым изгибом понимают такой, при котором нагрузки, действующие на балку, расположены в одной плоскости, которая не совпадает не с одной из главных плоскостей инерции. Для сечений, у которых моменты инерции относительно обеих ортогональных осей одинаковы, косой изгиб не возможен. У этих сечений все оси главные. Это сечения типа круг, труба, квадрат и т. д. Сложный изгиб Косой изгиб F 3 l y F 2 F 3 Fx F 3 M 1 x R 1 F 1 Вертикальная силовая плоскость Горизонтальная силовая симметрии F Fy

Сложный и косой изгиб Напряжения при сложном изгибе Напряжения при косом изгибе здесь: MX, MY – составляющие изгибающего момента; M - полный изгибающий момент в сечении; - угол между осью y и следом плоскости действия полного момента; x и у координаты точки, в которой определяют напряжения; Ix и Iy - моменты инерции поперечного сечения. При определении знака нормального напряжения необходимо придерживаться правила, по которому момент, вызывающий деформацию растяжения в первой четверти поперечного сечения считается положительным, тогда знак напряжения определяется знаком координат точки, в которой определяется напряжение. Условие прочности при сложном изгибе Условие прочности при косом изгибе

Сложный и косой изгиб Полный изгибающий момент связан с его составляющими зависимостями: где α – угол между осью y и плоскостью действия полного момента При косом изгибе нормальные напряжения в центре тяжести поперечного сечения равны нулю Следовательно, нейтральная ось при косом изгибе, так же как и прямом изгибе проходит через центр тяжести поперечного сечения
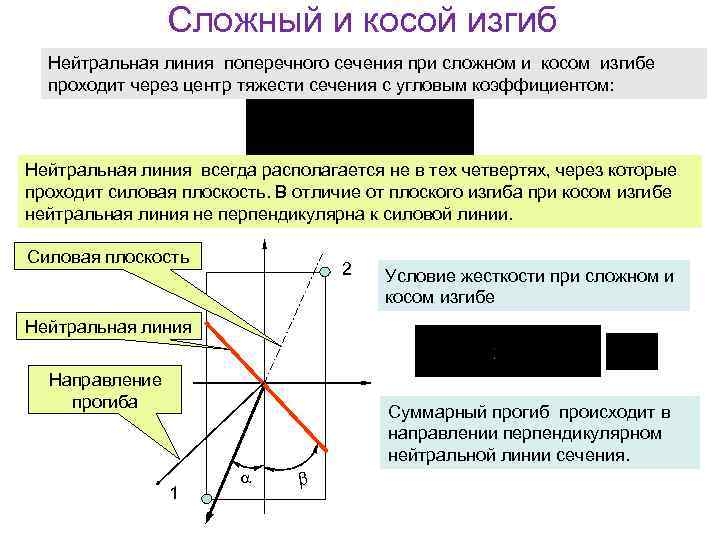
Сложный и косой изгиб Нейтральная линия поперечного сечения при сложном и косом изгибе проходит через центр тяжести сечения с угловым коэффициентом: Нейтральная линия всегда располагается не в тех четвертях, через которые проходит силовая плоскость. В отличие от плоского изгиба при косом изгибе нейтральная линия не перпендикулярна к силовой линии. Силовая плоскость 2 Условие жесткости при сложном и косом изгибе Нейтральная линия Направление прогиба Суммарный прогиб происходит в направлении перпендикулярном нейтральной линии сечения. 1
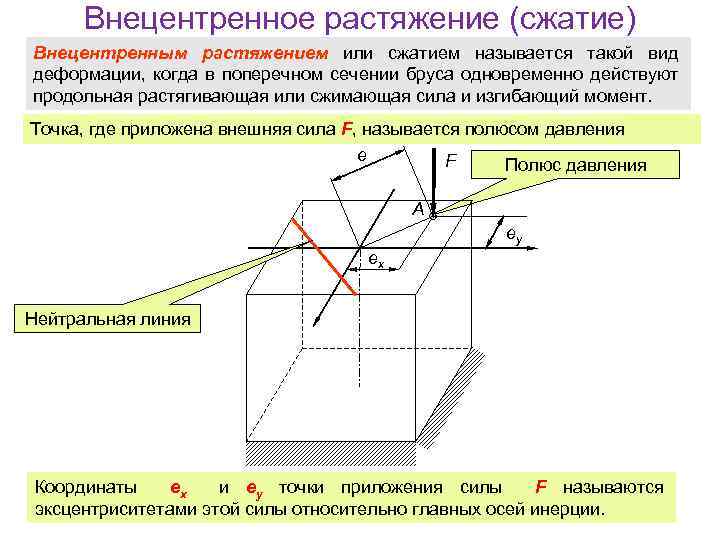
Внецентренное растяжение (сжатие) Внецентренным растяжением или сжатием называется такой вид деформации, когда в поперечном сечении бруса одновременно действуют продольная растягивающая или сжимающая сила и изгибающий момент. Точка, где приложена внешняя сила F, называется полюсом давления e F Полюс давления A ey ex Нейтральная линия Координаты ex и ey точки приложения силы F называются эксцентриситетами этой силы относительно главных осей инерции.

Внецентренное растяжение (сжатие) Внецентренно растянутый или сжатый брус, при расчете которого можно не учитывать дополнительные изгибающие моменты, равные произведениям продольных сил на прогибы, называется жестким, а брус, при расчете которого их следует учитывать, гибким Нормальные напряжения в произвольной точке сечения равно сумме напряжений от продольной силы и изгибающих моментов или : (1) Продольная сила N и изгибающие моменты могут рассматриваться как результат воздействия на брус внецентренно приложенной силы F=N (2) Получим Подставим в формулу (1) выражения: (3)

Внецентренное растяжение (сжатие) Формулу (3) можно представить в следующем виде (4) где радиусы инерции поперечного сечения бруса относительно главных центральных осей инерции Для определения положения нейтральной линии приравняем нулю выражение (4): (5) Выражение (5) представляет собой выражение нейтральной оси Выражение (5) является уравнением прямой, т. к. координаты x и y входят в него в первой степени
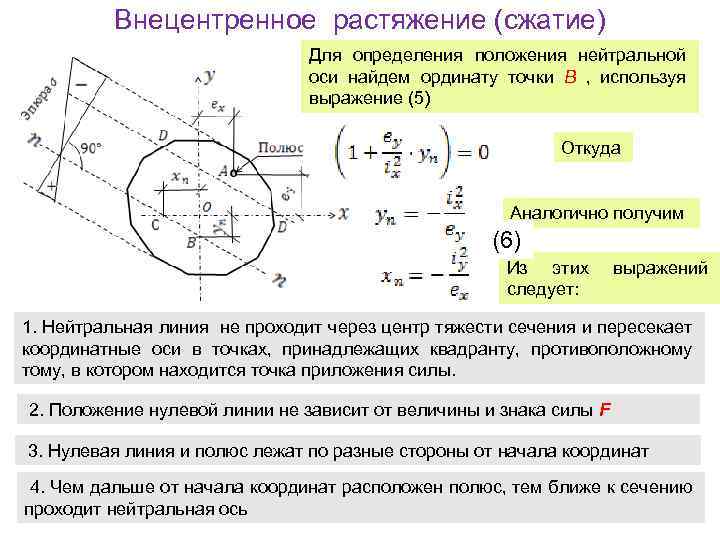
Внецентренное растяжение (сжатие) Для определения положения нейтральной оси найдем ординату точки В , используя выражение (5) Откуда Аналогично получим (6) Из этих следует: выражений 1. Нейтральная линия не проходит через центр тяжести сечения и пересекает координатные оси в точках, принадлежащих квадранту, противоположному тому, в котором находится точка приложения силы. 2. Положение нулевой линии не зависит от величины и знака силы F 3. Нулевая линия и полюс лежат по разные стороны от начала координат 4. Чем дальше от начала координат расположен полюс, тем ближе к сечению проходит нейтральная ось

Внецентренное растяжение (сжатие) 5. Если полюс расположен на одной из главных центральных осей инерции, то нулевая линия перпендикулярна к этой оси При внецентренном растяжении и сжатии нормальные напряжения в каждой точке поперечного сечения бруса, как и при изгибе, прямо пропорциональны расстоянию от этой точки до нейтральной оси Наибольшие напряжения возникают в точках поперечного сечения, наиболее удаленных от нейтральной оси Для определения положения опасных точек в сечении следует параллельно нейтральной оси провести линии, касающиеся контура сечения Ядром сечения называется некоторая центральная область, обладающая тем свойством, что сжимающая сила, приложенная в любой ее точке, вызывает во всех точках поперечного сечения бруса сжимающие напряжения, т. е. напряжения одного знака

Ядро сечения Если сила приложена за пределами ядра сечения, то в поперечном сечении возникают и сжимающие, и растягивающие напряжения Если сила приложена на границе ядра сечения, то нулевая линия касается контура сечения (в месте касания нормальные напряжения равны нулю) При расчете внецентренно сжатых элементов по эксцентриситету сжимающей силы, не вычисляя величин напряжений, устанавливать возникнут ли в поперечном сечении растягивающие напряжения или нет Порядок построения ядра сечения 1. Определение положения центра тяжести сечения и главных центральных осей 2. Определение главных моментов инерции и квадратов радиусов инерции 3. Если сечение имеет вид многоугольника, то вершины его углов последовательно рассматривать как полюсы и для каждого такого полюса определять положение нулевой линии (контур, ограниченный нулевыми линиями, образует ядро сечения) 4. Если многоугольное сечение имеет внутренние углы, то эти углы при обходе вершин не рассматривают как полюсы

Ядро сечения Построим ядро сечения для прямоугольника Примем в качестве полюса вершину А 1 По формулам (6) найдем отрезки, отсекаемые соответствующей этому полюсу нулевой линией a 1 на осях координат: По значениям этих отрезков построена нулевая линия a 1 Учитывая симметрию прямоугольного сечения относительно координатных осей строим остальные нулевые линии при соответствующих полюсах Построенные нулевые линии образуют заштрихованное ядро сечения
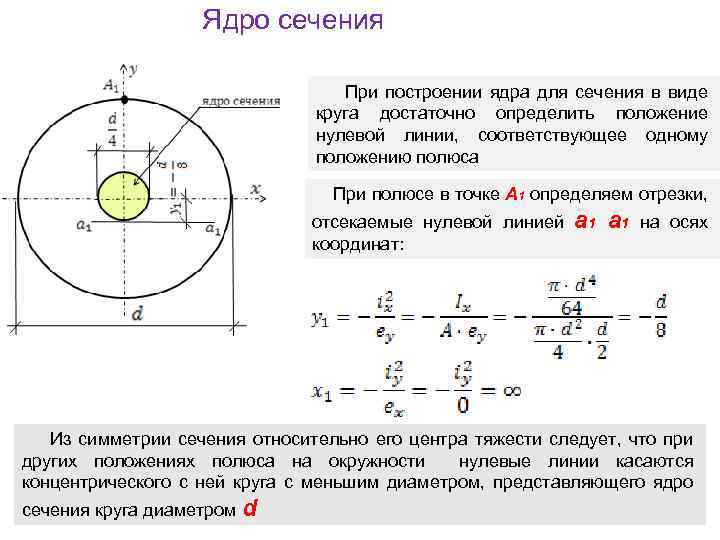
Ядро сечения При построении ядра для сечения в виде круга достаточно определить положение нулевой линии, соответствующее одному положению полюса При полюсе в точке А 1 определяем отрезки, отсекаемые нулевой линией координат: a 1 на осях Из симметрии сечения относительно его центра тяжести следует, что при других положениях полюса на окружности нулевые линии касаются концентрического с ней круга с меньшим диаметром, представляющего ядро сечения круга диаметром d
Лекция 7. Сложное сопротивление.ppt