Сложение элементов симметрии дисконтинуума Как и в случае

Сложение элементов симметрии дисконтинуума Как и в случае точечных групп, взаимодействие двух элементов симметрии бесконечных фигур приводит к возникновению третьего элемента. Элементы симметрии дисконтинуума: 1. центр инверсии (симметрии): 2. плоскость зеркального отражения: 3. оси симметрии: 4. трансляция: 5. плоскости скользящего отражения : 6. винтовые оси :

Последовательное отражение в двух параллельных плоскостях Теорема 1. Последовательное отражение в двух параллельных плоскостях симметрии равносильно трансляции с параметром равным удвоенному расстоянию между плоскостями. Теорема 1 а (обратная). Любую трансляцию можно заменить двумя последовательными отражениями в параллельных плоскостях симметрии, отстоящих друг от друга на расстоянии, равном половине параметра трансляции. AO=OB и BP=PC AC=AO+OB+BP+PC=2 a= t. Если есть плоскость симметрии, то обязательно будет и вторая, но наличие трансляции не означает существования двух плоскостей!

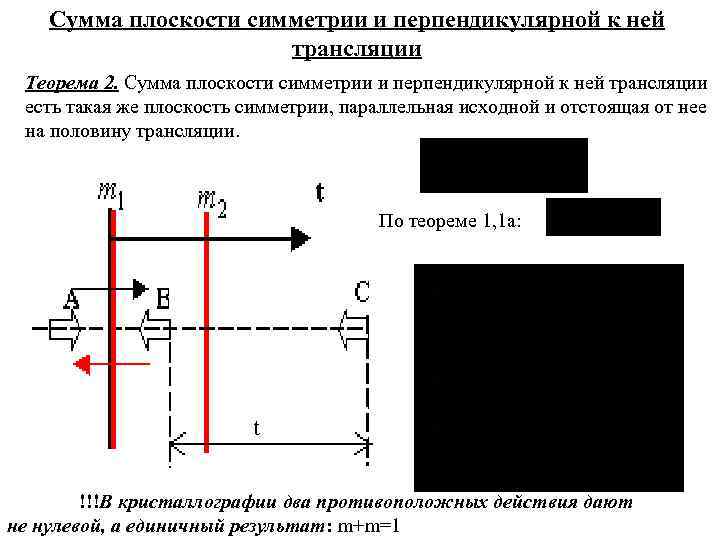Сумма плоскости симметрии и перпендикулярной к ней трансляции Теорема 2. Сумма плоскости симметрии и перпендикулярной к ней трансляции есть такая же плоскость симметрии, параллельная исходной и отстоящая от нее на половину трансляции. По теореме 1, 1 а: t !!!В кристаллографии два противоположных действия дают не нулевой, а единичный результат: m+m=1

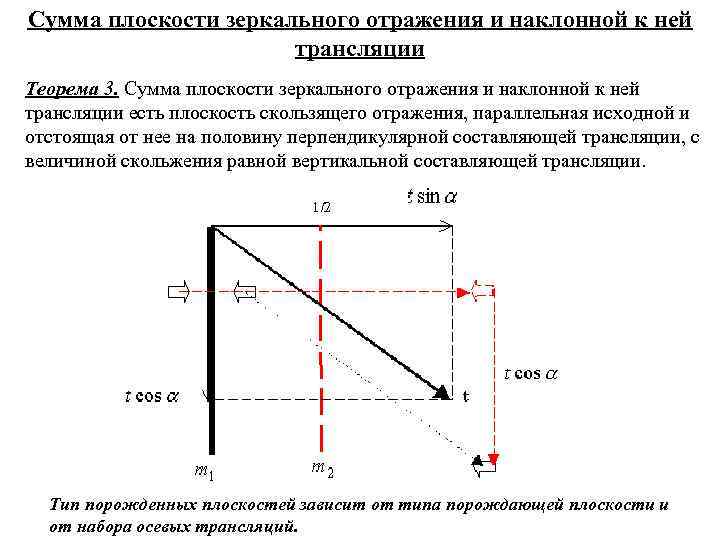Сумма плоскости зеркального отражения и наклонной к ней трансляции Теорема 3. Сумма плоскости зеркального отражения и наклонной к ней трансляции есть плоскость скользящего отражения, параллельная исходной и отстоящая от нее на половину перпендикулярной составляющей трансляции, с величиной скольжения равной вертикальной составляющей трансляции. Тип порожденных плоскостей зависит от типа порождающей плоскости и от набора осевых трансляций.

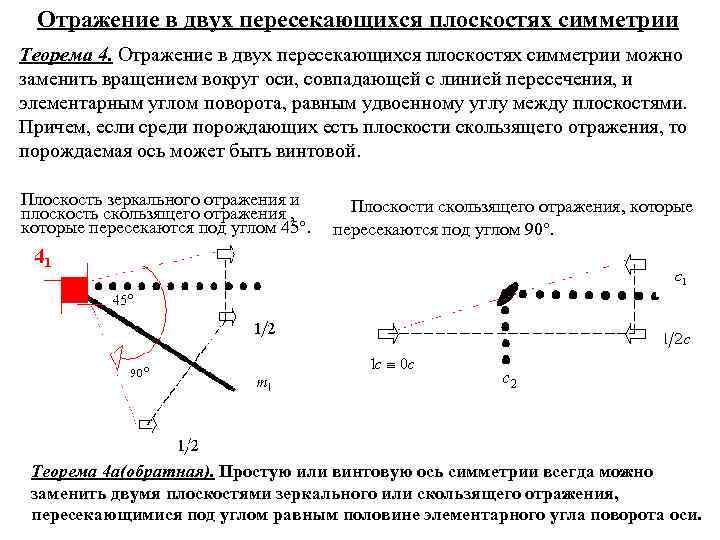Отражение в двух пересекающихся плоскостях симметрии Теорема 4. Отражение в двух пересекающихся плоскостях симметрии можно заменить вращением вокруг оси, совпадающей с линией пересечения, и элементарным углом поворота, равным удвоенному углу между плоскостями. Причем, если среди порождающих есть плоскости скользящего отражения, то порождаемая ось может быть винтовой. Плоскость зеркального отражения и плоскость скользящего отражения , которые пересекаются под углом 45. Плоскости скользящего отражения, которые пересекаются под углом 90. Теорема 4 а(обратная). Простую или винтовую ось симметрии всегда можно заменить двумя плоскостями зеркального или скользящего отражения, пересекающимися под углом равным половине элементарного угла поворота оси.

Сумма оси симметрии и перпендикулярной к ней трансляции Теорема 5. Сумма оси симметрии и перпендикулярной к ней трансляции есть такая же ось симметрии, параллельная исходной и отстоящая от нее на расстоянии равном в направлении, составляющем с трансляцией угол. Где, N - элементарный угол поворота оси симметрии. По теореме 4 : 2=m 1+m 2 По теореме 1 а: t= m 1+m 3 В результате получаем: 2+t = m 1+m 2+ m 1+m 3 = =1+ m 2+ m 3 =1+N=N Вновь полученная ось лежит в направлении, составляющем с трансляцией угол равный на расстоянии

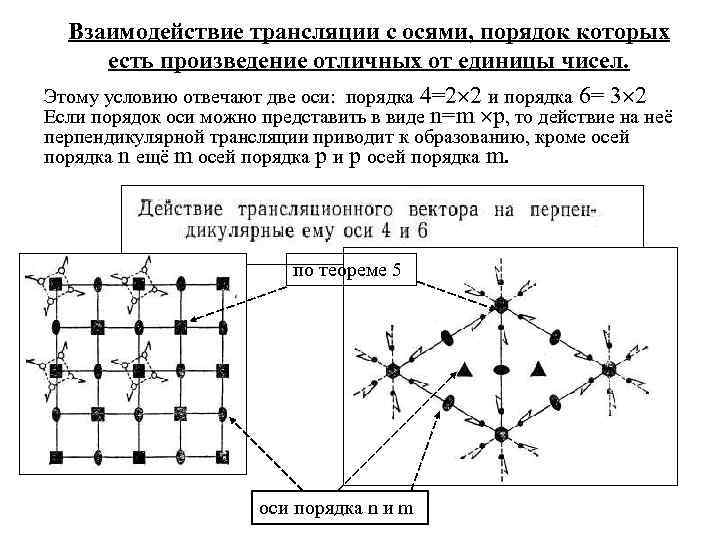Взаимодействие трансляции с осями, порядок которых есть произведение отличных от единицы чисел. Этому условию отвечают две оси: порядка 4=2 2 и порядка 6= 3 2 Если порядок оси можно представить в виде n=m p, то действие на неё перпендикулярной трансляции приводит к образованию, кроме осей порядка n ещё m осей порядка p и p осей порядка m. по теореме 5 оси порядка n и m