Словари Линейные алгоритмы выполнения операций со словарём

Словари. Линейные алгоритмы выполнения операций со словарём.

Определение • Структура данных, обеспечивающая выполнение операций ПРИНАДЛЕЖАТЬ, ВСТАВИТЬ и УДАЛИТЬ, будет называться словарем. • Алгоритмы для каждой из операций будем рассматривать на примере 2 -3 дерева

Вставка нового элемента в 2 -3 дерево • Чтобы в 2 -3 -дерево вставить новый элемент а, надо найти место для нового листа l, который будет содержать а. Для этого ищут элемент а в дереве. Если дерево содержит более одного элемента, то поиск а окончится в узле f, имеющем двух или трех сыновей, которые являются листьями. • Если из узла f выходит только два листа l 1 и l 2, то l делаем сыном узла f. Если a

• Теперь предположим, что у f уже есть три листа l 1 и l 2 и l 3. Сделаем I надлежащим сыном узла f. Теперь f имеет четырех сыновей. Чтобы сохранить 2 -3 свойство, образуем новый узел g. Два левых сына оставим сыновьями узла f, а два правых переделаем в сыновей узла g. Затем сделаем g братом узла f, сделав его сыном отца узла f. Если отец узла f имел двух сыновей, то на этом мы остановимся. Если же трех, то надо рекурсивно повторять эту процедуру до тех пор, пока у всех узлов в дереве останется не более трех сыновей. Если у корня окажется четыре сына, образуем новый корень с двумя новыми сыновьями, каждый из которых будет иметь в качестве двух своих сыновей двух из четырех сыновей старого корня.

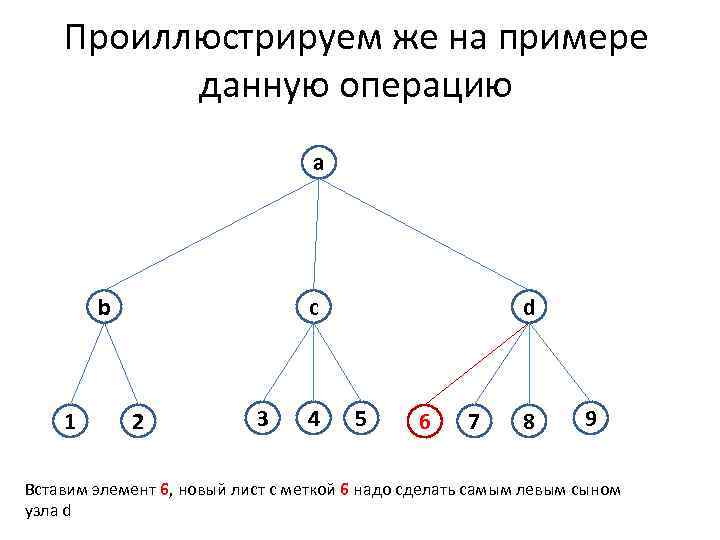Проиллюстрируем же на примере данную операцию a b 1 c 2 3 4 d 5 6 7 8 9 Вставим элемент 6, новый лист с меткой 6 надо сделать самым левым сыном узла d

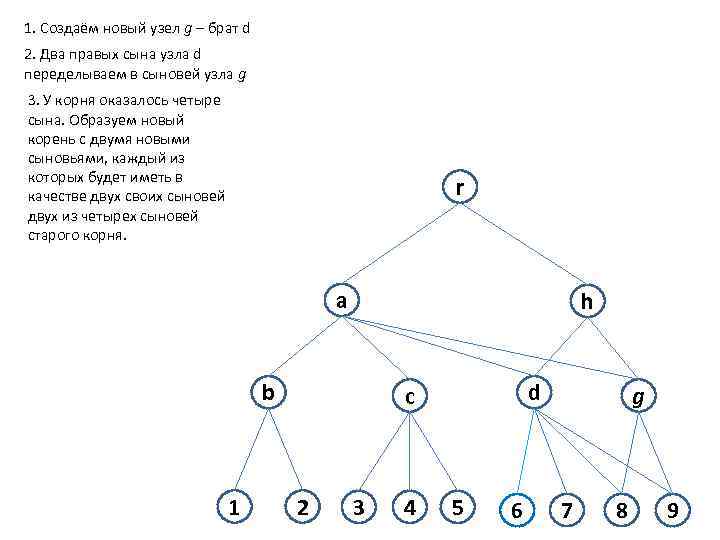1. Создаём новый узел g – брат d 2. Два правых сына узла d переделываем в сыновей узла g 3. У корня оказалось четыре сына. Образуем новый корень с двумя новыми сыновьями, каждый из которых будет иметь в качестве двух своих сыновей двух из четырех сыновей старого корня. r a h b 1 d c 2 3 4 5 6 g 7 8 9

Теорема • Данный алгоритм вставляет новый элемент в 2 -3 -дерево с n листьями за время, не превосходящее О (log n). Более того, этот алгоритм сохраняет порядок исходных листьев и структуру 2 -3 -дерева.

Удаление элемента из 2 -3 дерева • Элемент а можно удалить из 2 -3 -дерева способом, по существу обратным к вставке. Пусть а — метка листа l. Рассмотрим отдельно три случая. • Случай 1. Если l — корень, удаляем его. (В этом случае а был единственным элементом в дереве. ) • Случай 2. Если l — сын узла, имеющего трех сыновей, удаляем его. • Случай 3. Если l — сын узла, имеющего двух сыновей s и I, то может быть одно из двух: а) f — корень; удаляем l и f и делаем корнем второго сына s; б) f — не корень. Допустим, что f имеет брата слева от себя. Случай, когда брат находится справа, рассматривается аналогично. Если у g только два сына, делаем узел s самым правым сыном узла g, удаляем l и рекурсивно вызываем процедуру удаления, чтобы удалить f. Если у g три сына, то самого правого сына делаем левым сыном узла f и удаляем l.

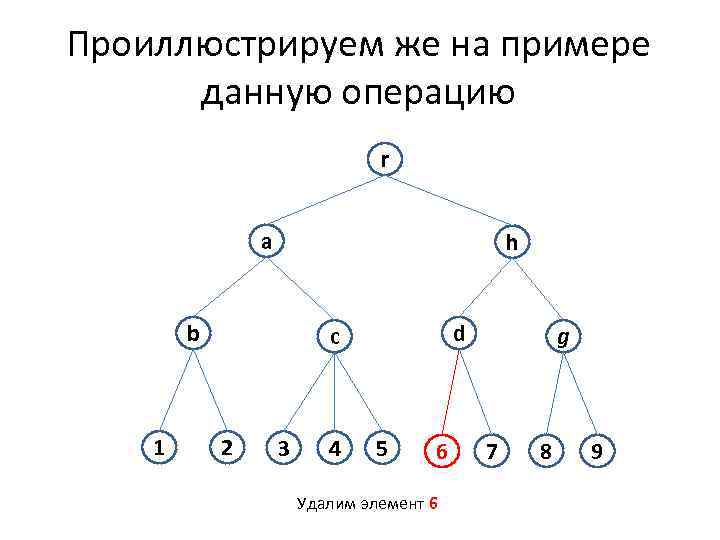Проиллюстрируем же на примере данную операцию r a h b 1 d c 2 3 4 5 6 Удалим элемент 6 g 7 8 9

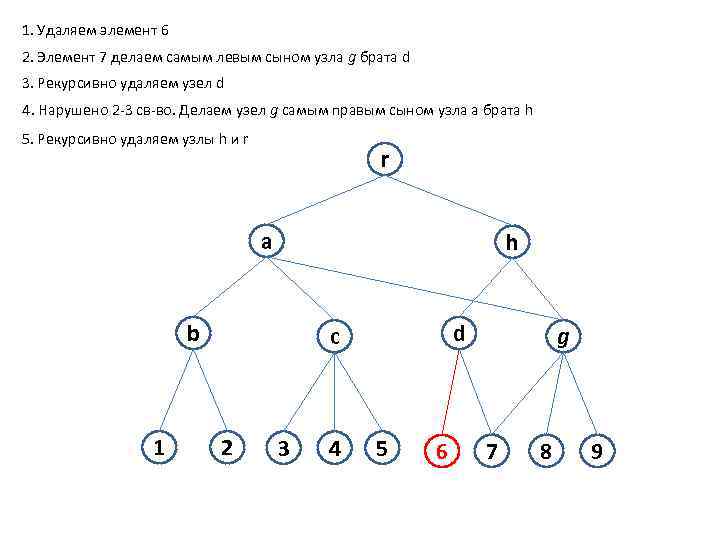1. Удаляем элемент 6 2. Элемент 7 делаем самым левым сыном узла g брата d 3. Рекурсивно удаляем узел d 4. Нарушено 2 -3 св-во. Делаем узел g самым правым сыном узла a брата h 5. Рекурсивно удаляем узлы h и r r a h b 1 d c 2 3 4 5 6 g 7 8 9

Операция ПРИНАДЛЕЖАТЬ • Для выполнения операции ПРИНАДЛЕЖАТЬ достаточен следующий алгоритм: • Вход. 2 -3 Дерево Т для множества S и элемент а. • Выход. "Да", если a принадлежит S, и "нет" в противном случае. • Метод. Если дерево Т пусто, выдать "нет. " В противном случае пусть г — корень дерева Т. Тогда алгоритм состоит из единственного вызова ПОИСК(а, г) рекурсивной процедуры ПОИСК, приведенной ниже

procedure ПОИСК(а, г): • if любой сын узла г является листом then return г • else • begin • пусть s[i]- будет i-м сыном узла г; • if a<=L[r] then return ПОИСК(а, s[1]) • else • if у г два сына или a<=M[r] then return ПОИСК(а, s[2]) • else return ПОИСК(а, s[3]) • end

• Итак, операции ПРИНАДЛЕЖАТЬ, ВСТАВИТЬ и УДАЛИТЬ на 2 -3 -дереве с n листьями можно выполнить не более чем за О (log n) шагов. Следовательно, 2 -3 -дерево может служить словарем с производительностью О (n log n), ибо оно может обеспечить выполнение последовательности из n операций ПРИНАДЛЕЖАТЬ, ВСТАВИТЬ и УДАЛИТЬ не более чем за О (n log n) шагов.

Сливаемые деревья. Линейные алгоритмы выполнения операций со сливаемыми деревьями.

Определение • Структура данных, обеспечивающая выполнение операций ВСТАВИТЬ, УДАЛИТЬ, MIN, ОБЪЕДИНИТЬ, будет называться сливаемым деревом. • Операции ВСТАВИТЬ и УДАЛИТЬ мы уже рассмотрели. Рассмотрим же теперь оставшиеся операции MIN и ОБЪЕДИНИТЬ.

Операция MIN • Для выполнения этой операции потребуется единственная функция НАИМЕНЬШИЙ. • Каждый внутренний узел дерева Т пометим значением НАИМЕНЬШИЙ[v], т. е. значением наименьшего элемента, хранящегося в поддереве с корнем v. • Наименьший элемент множества S можно найти, если следующим образом двигаться вниз по дереву Т, начиная от его корня. Находясь во внутреннем узле v, переходим к сыну узла v, помеченному наименьшим значением функции НАИМЕНЬШИЙ. Следовательно, если Т содержит n листьев, то операция MIN занимает О (log n) шагов.

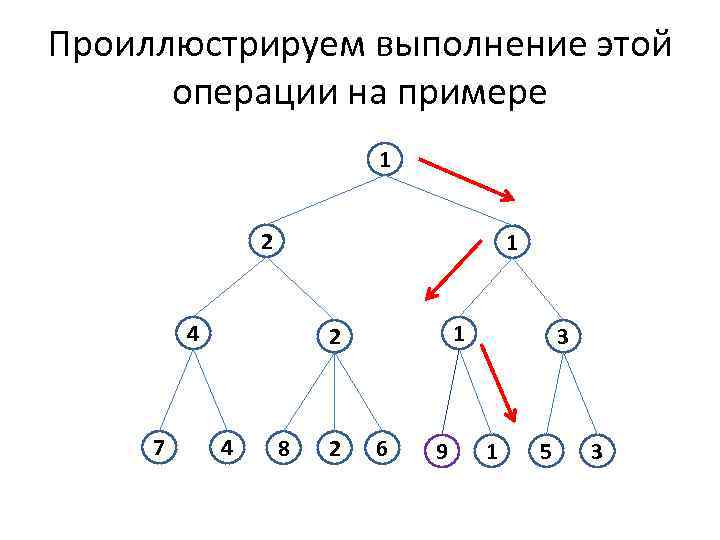Проиллюстрируем выполнение этой операции на примере 1 2 1 4 7 1 2 4 8 2 6 9 3 1 5 3

Операция ОБЪЕДЕНИТЬ • Каждое множество представлено отдельным 2 -3 -деревом. Чтобы слить два множества S 1 и S 2, вызываем процедуру ИМПЛАНТАЦИЯ(T 1, Т 2), приведенную ниже, где Т 1 и Т 2 — это 2 -3 -деревья, представляющие S 1 и S 2.

Procedure ИМПЛАНТАЦИЯ(Т 1, Т 2) • • • • if ВЫСОТА(Т 1) = ВЫСОТА(Т 2) then begin образовать новый корень г; сделать КОРЕНЬ[T 1] и КОРЕНЬ[Т 2] соответственно левым и правым сыновьями узла г; end else wig положим ВЫСОТА(T 1) > ВЫСОТА(Т 2) otherwise переставить T 1 с Т 2 и "левый" с "правым" in begin пусть v—такой узел на самом правом пути в T 1, что ГЛУБИНА(v) = ВЫСОТА(Т 1) —ВЫСОТА(Т 2); пусть f—отец узла v; сделать КОРЕНЬ[T 2] сыном узла f, расположенным непосредственно справа от v; if у f сейчас четыре сына then ДОБАВСЫНА(f) end

procedure ДОБАВСЫНА (v) • • • • begin образовать новый узел v‘; сделать двух самых правых сыновей узла v левым и правым сыновьями узла v‘; if у v нет отца then begin образовать новый корень г; сделать v левым, а v' правым сыном корня г end else begin пусть f—отец узла v; сделать v' сыном узла f, расположенным непосредственно справа от v; if теперь у f четыре сына then ДОБАВСЫНА(f) end

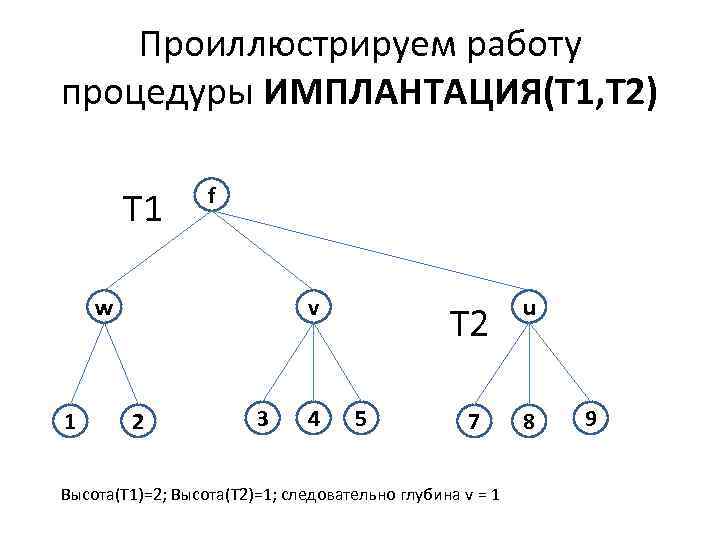Проиллюстрируем работу процедуры ИМПЛАНТАЦИЯ(Т 1, Т 2) T 1 f w 1 v 2 3 4 T 2 5 u 7 8 Высота(Т 1)=2; Высота(Т 2)=1; следовательно глубина v = 1 9

• Процедура ИМПЛАНТАЦИЯ соединяет T 1 и Т 2 в одно 2 -3 дерево за время О(h 1—h 2) (при h 1>h 2).

Сцепляемые очереди. Линейные алгоритмы выполнения операций со сцепляемыми очередями.

Определение • Структура данных, обеспечивающая выполнение операций ВСТАВИТЬ, УДАЛИТЬ, НАЙТИ, СЦЕПИТЬ, РАСЦЕПИТЬ, будет называться сцепляемой очередью. • Операции ВСТАВИТЬ и УДАЛИТЬ мы уже рассмотрели. Операция НАЙТИ осуществляется рассмотренной процедурой ПОИСК. Рассмотрим же теперь оставшиеся операции СЦЕПИТЬ и РАСЦЕПИТЬ.

Операция СЦЕПИТЬ • Операции СЦЕПИТЬ(S 1, S 2) на вход подаются такие две последовательности S 1 и S 2, что каждый элемент из S 1 меньше каждого элемента из S 2; на выход она выдает конкатенацию этих последовательностей, т. е. S 1 S 2. Если S 1 и S 2 представлены соответственно 2 -3 -деревьями T 1 и T 2, то мы хотим соединить T 1 и Т 2 в одно дерево Т, листьями которого являются листья дерева T 1 в их первоначальном порядке и следующие за ними листья дерева Т 2 в их первоначальном порядке. Это можно осуществить, вызвав процедуру ИМПЛАНТАЦИЯ(T 1, Т 2).

Операция РАСЦЕПИТЬ • Операция РАСЦЕПИТЬ(а, S) разбивает S на два множества S 1={b|b<=a и b принадлежащих S} и S 2={b|b>a и b принадлежащих S}. Для ее реализации определим процедуру ДЕЛЕНИЕ (а, Т), которая расцепляет 2 -3 -дерево Т на два такие 2 -3 -дерева T 1 и Т 2, что метки всех листьев в T 1 не больше а, а метки всех листьев в Т 2 больше а.

procedure ДЕЛЕНИЕ(a, T) • • • • • begin на пути из узла КОРЕНЬ[T] к листу с меткой а удалить все узлы, кроме этого листа; comment В данный момент дерево Т оказалось разделенным на два леса—левый, состоящий из всех деревьев, листья которых лежат слева от а, и из узла с меткой а, и правый, состоящий из всех деревьев, листья которых лежат справа от а; while в левом лесу более одного дерева do begin пусть T’ и Т"—два самых правых дерева в левом лесу; ИМПЛАНТАЦИЯ ( Т’, T”) end; while в правом лесу более одного дерева do begin пусть T’ и Т"—два самых левых дерева в правом лесу; ИМПЛАНТАЦИЯ(T’, T”) end

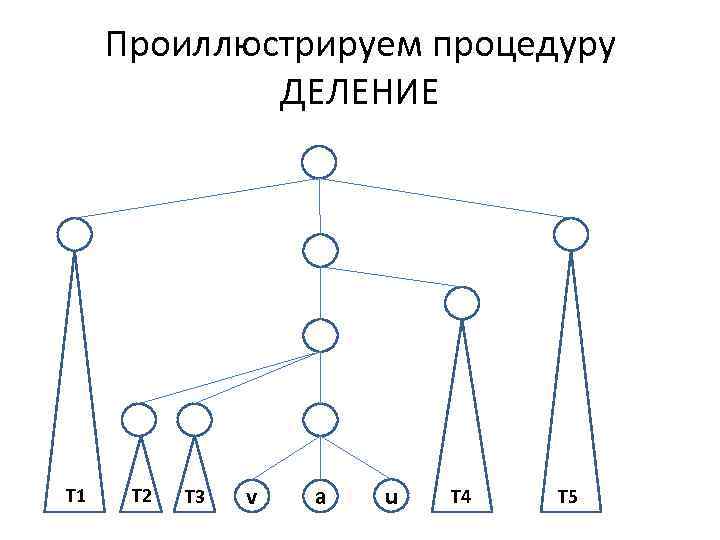Проиллюстрируем процедуру ДЕЛЕНИЕ Т 1 T 2 T 3 v a u T 4 T 5

Теорема • Процедура ДЕЛЕНИЕ разбивает 2 -3 -дерево Т по листу а так, что все листья слева от а и сам лист а оказываются в одном 2 -3 дереве, а все листья справа от а — в другом. Эта процедура занимает время О (ВЫСОТА(Т)). Порядок листьев cохраняется.