Slides to accompany Weathington Cunningham Pittenger 2010

Slides to accompany Weathington, Cunningham & Pittenger (2010), Chapter 13: Between-Subjects Factorial Designs 1

Objectives • Two-variable design • GLM and two-variable design • Advantages of 2 -variable design • Main effects • Interactions • Designing a two-variable study 2

Two-Variable Design • Relationship between two IV and a DV – How much does each IV influence DV? – How much do the IVs together influence DV? 3

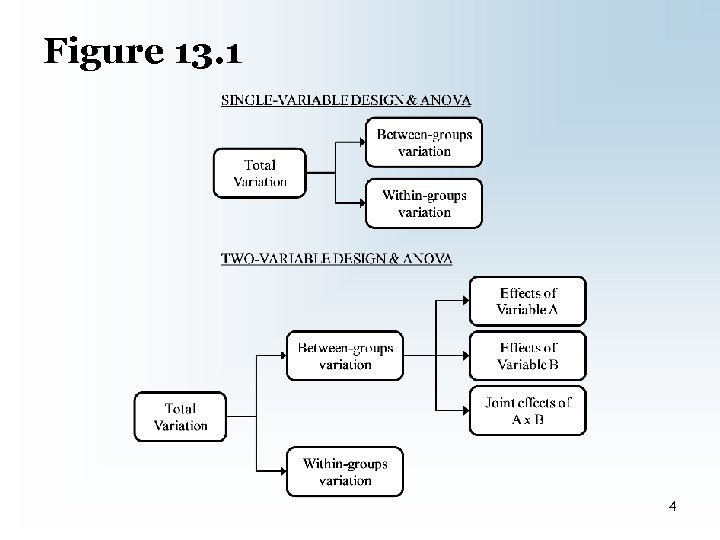Figure 13. 1 4

GLM and Two-Variable Design • Single-variable, Xij = µ + αj + εij • Now, Xij = µ + αj + βk + αβjk + εijk 5

Advantages of 2 -Variable Design • Efficiency – Fewer people, more power to examine more questions simultaneously – See Table 13. 1 • Can consider interaction of variables – Influence of variable combinations • Increased power – W-g variance < in one-group design 6

A Bit More on Interactions • Pattern of results unexplainable by a single IV by itself – Compare Figure 13. 2 with 13. 3 7

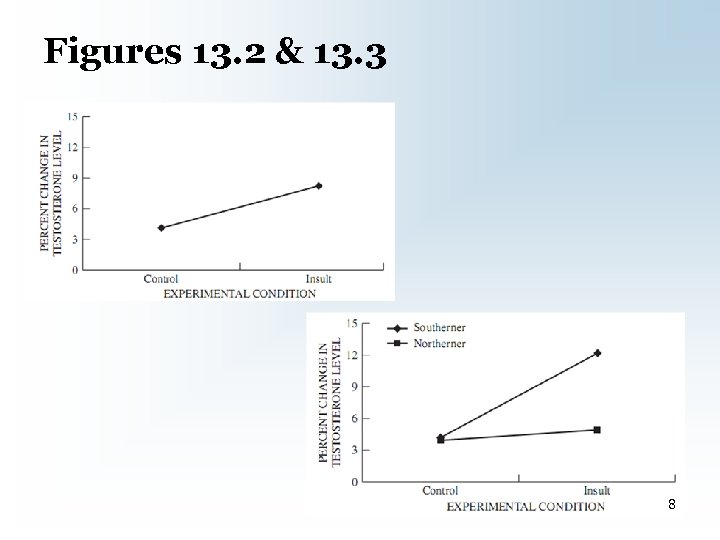Figures 13. 2 & 13. 3 8

Variables, Levels, Cells • Factorial design = study with independent groups for each possible combination of levels of the IV – e. g. , A x B, 2 x 2, 3 x 4 • Can have more than 2 variables (A x B x C) – Here we consider A x B 9

Example • From text, “Reaction to Product Endorsement” • DV = Willingness to buy • IV A = source credibility (high vs. low) • IV B = type of review (strong, ambiguous, and weak) • 2 x 3 factorial design (Figure 13. 4) • Interaction of A x B 10

Main Effects • Effect of one IV on the DV, holding the other IV constant • Special form of b-g variance • Two-factor design has two main effects – Fig. 13. 8 and 13. 9(a) = significant findings – Fig. 13. 9(b) = nonsignificant findings 11

Figure 13. 8 12

Figure 13. 9 13

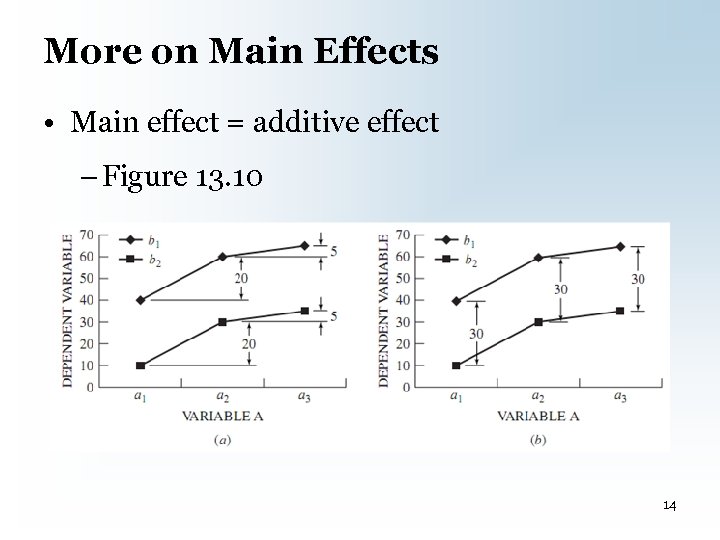More on Main Effects • Main effect = additive effect – Figure 13. 10 14

More on Interactions • Interaction = interplay between two variables – Figures 13. 11 and 13. 12 • When you have a significant interaction, interpret mean differences carefully 15

Figure 13. 11 16

Figure 13. 12 17

Designing a Factorial Study • Each participant in only one IV combo condition • At least 2 levels of each IV – Sometimes more levels is better • Best to have a DV with an interval or ratio scale (easier than nominal/ordinal) • Try for equal n across each tx condition 18

Estimating Sample Size • Can be accomplished with power analysis • See the appropriate table in Appendix B – Effect size estimate, f – Desired power – Three F-ratios in a two-factor design: A, B, Ax. B • Plan for sample size needed for weakest effect – Formula for estimating n’ is Equation 13. 2 19

Interpreting Interactions • Residual = effect of interaction after removing influence of the main effects Δij = Mij – Mai – Mbj + Moverall – If interaction not statistically significant then residual (Δij) will be close to 0 – Stronger interactions lead to larger residuals in multiple treatment conditions 20

Interpreting Interactions • Residuals represent the effects of the interaction on the DV that are not explained by the individual main effects alone • When no interaction is present, the residuals for each treatment condition will be close to or equal to 0 • Table 13. 7 and Figure 13. 14 illustrate 21

Table 13. 7 22

Figure 13. 14 23

What is Next? • **instructor to provide details 24