Sld 8. Drzewa.12.2012.ppt
- Количество слайдов: 22
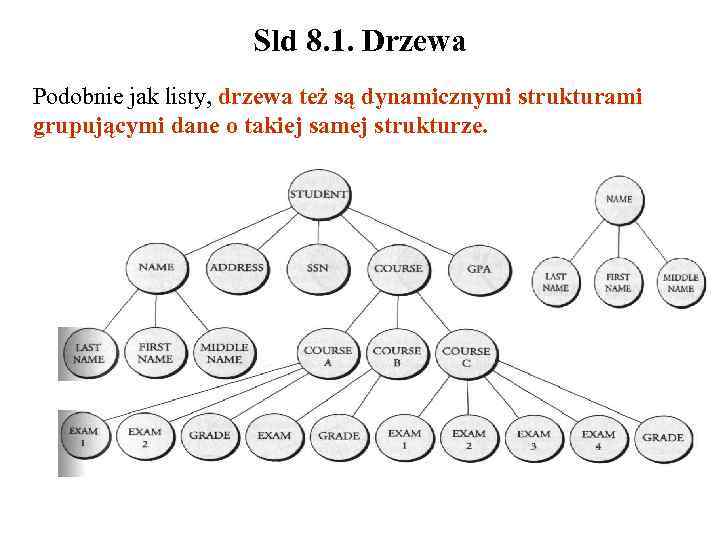
Sld 8. 1. Drzewa Podobnie jak listy, drzewa też są dynamicznymi strukturami grupującymi dane o takiej samej strukturze.

Sld 8. 2. Drzewa • Drzewo składa się z korzenia (przedstawianego, podobnie jak w matematyce i informatyce, zwykle u góry rysunku) oraz gałęzi prowadzących z korzenia do kolejnych węzłów. • W każdym węźle sprawdzany jest pewien warunek dotyczący danej obserwacji, i na jego podstawie wybierana jest jedna z gałęzi prowadząca do kolejnego węzła piętro niżej. • Na dole znajdują się liście, w których odczytujemy do której z klas należy przypisać daną obserwację. Klasyfikacja danej obserwacji polega na przejściu od korzenia do liścia i przypisaniu do tej obserwacji klasy zapisanej w danym liściu.

Sld 8. 3. Drzewa • Schemat drzewa, w którym każdy wierzchołek ma co najwyżej trzy wierzchołki potomne (następniki), został pokazany na rysunku. • Ograniczenie liczby wierzchołków potomnych wynika ze statycznego charakteru struktury wierzchołka drzewa: struktura zawiera stałą liczbę wskaźników do wierzchołków potomnych. • Możliwości nawigacji po strukturze drzewa są ograniczone. Można się poruszać wzdłuż ścieżek od korzenia do liści. Nawigacja wzdłuż ścieżek w kierunku od liści do korzenia jest możliwa, jeśli struktura wierzchołka zostanie wyposażona w dodatkowy wskaźnik do wierzchołka poprzednika.

Sld 8. 4. Drzewa binarne Przypadkiem szczególnym drzew są drzewa binarne, to znaczy takie drzewa, w których każdy wierzchołek ma co najwyżej dwa wierzchołki potomne. W miejsce jednego wskaźnika następny (jak w liście jednokierunkowej) mamy do czynienia z dwoma wskaźnikami o nazwach lewy i prawy, będącymi wskaźnikami do lewej i prawej gałęzi drzewa binarnego. Podstawowa komórka do konstrukcji drzewa binarnego ma postać: struct wezel { int info; // lub dowolny inny typ danych struct wezel *lewy, *prawy; }
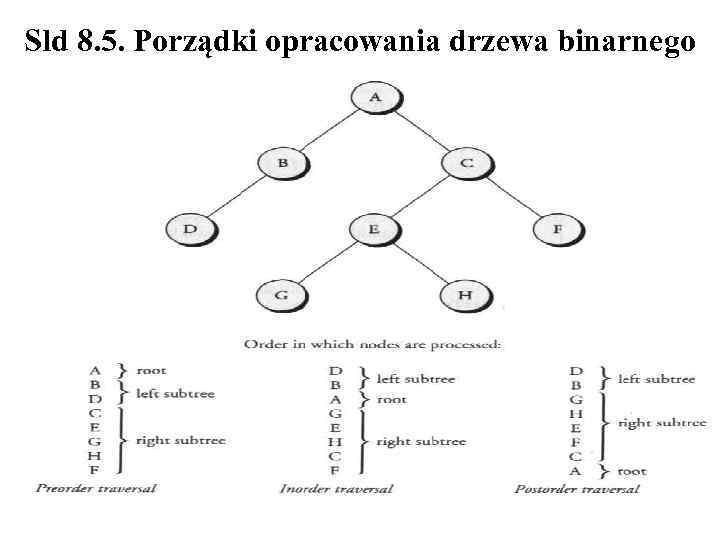
Sld 8. 5. Porządki opracowania drzewa binarnego

8. 6. Porządki opracowania drzewa binarnego Istnieje 6 sposobów przejścia drzewa binarnego: VLR, LVR, LRV, VRL, RVL, RLV, gdzie: Visit - "odwiedź" węzeł, Left - idź w lewo, Right - idź w prawo. Wyróżnia się 3 pierwsze: • VLR - pre-order, przejście wzdłużne • LVR - in-order, przejście poprzeczne • LRV - post-order, przejście wsteczne • • W przypadku gdy dane drzewo jest binarnym drzewem AST przejścia określa się również: pre-order - prefiksowym, gdyż wynik odwiedzania poszczególnych węzłów jest trawestacją wyrażenia zawartego w strukturze AST do postaci przedrostkowej (notacji Łukasiewicza) in-order - infiksowym, gdyż trawestuje wyrażenie do postaci wrostkowej post-order - postfiksowym, gdyż trawestuje wyrażenie do postaci przyrostkowej (odwrotnej notacji polskiej)
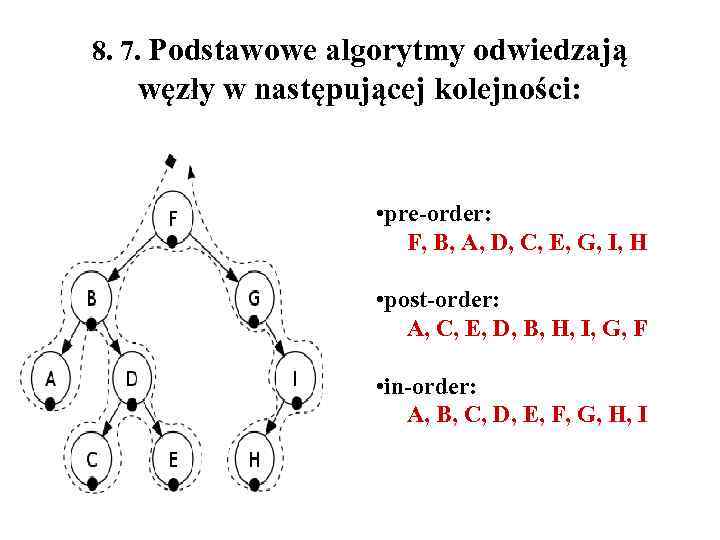
8. 7. Podstawowe algorytmy odwiedzają węzły w następującej kolejności: • pre-order: F, B, A, D, C, E, G, I, H • post-order: A, C, E, D, B, H, I, G, F • in-order: A, B, C, D, E, F, G, H, I
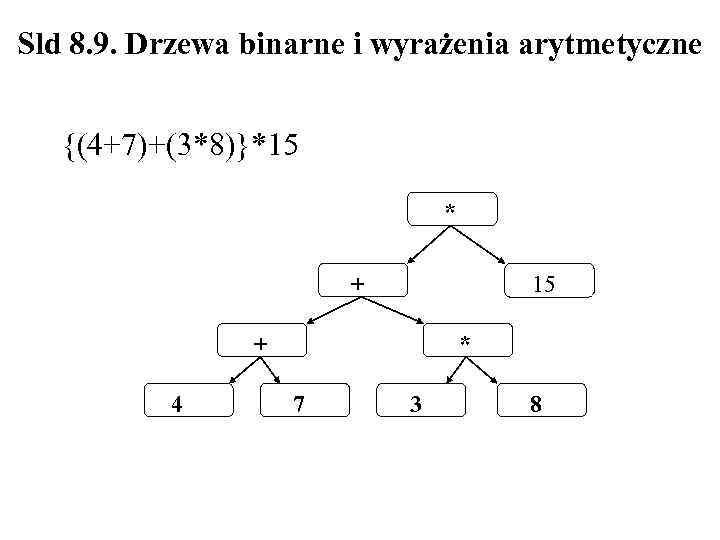
Sld 8. 9. Drzewa binarne i wyrażenia arytmetyczne {(4+7)+(3*8)}*15 * + 15 + * 4 7 3 8
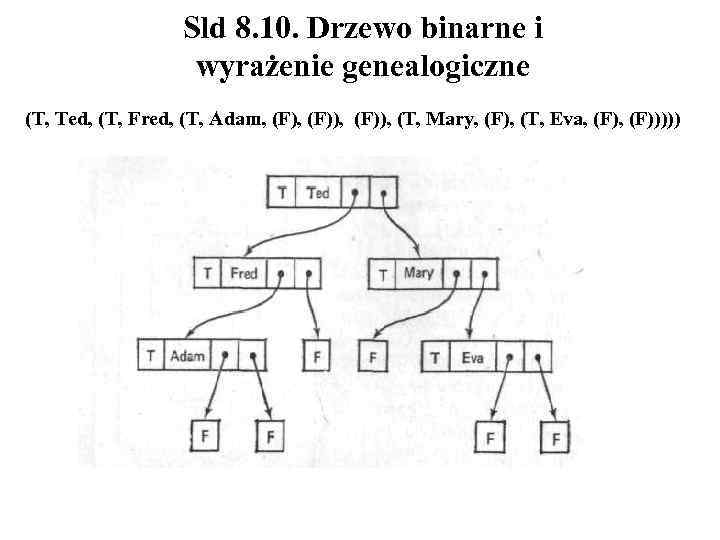
Sld 8. 10. Drzewo binarne i wyrażenie genealogiczne (T, Ted, (T, Fred, (T, Adam, (F)), (T, Mary, (F), (T, Eva, (F)))))

Sld 8. 11. Typy węzłów w drzewie opisującym wyrażenie arytmetyczne Struktura danych jest zwykłym drzewem binarnym, posiadającym dwa pola przeznaczone do przechowywania danych (operator i val) oraz tradycyjne wskaźniki do lewego i prawego odgałęzienia drzewa. Typy węzłów: 1. 2. wartości (listek drzewa) i operatora arytmetycznego, wiążącego w ogólnym przypadku trzy typy węzłów:
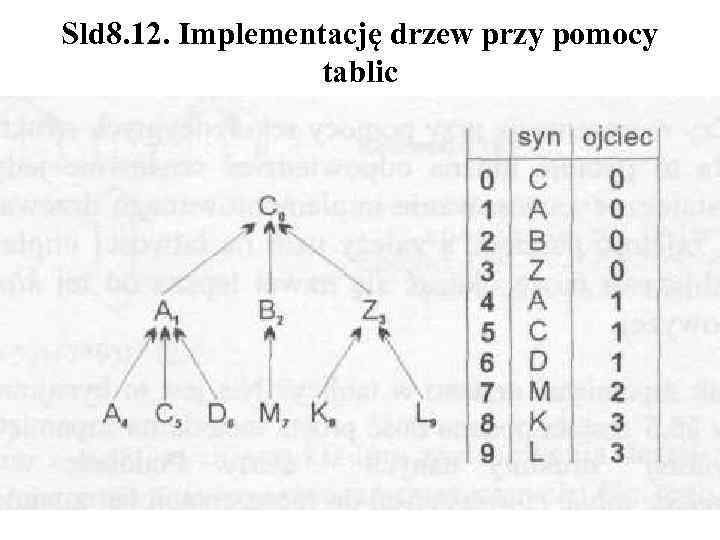
Sld 8. 12. Implementację drzew przy pomocy tablic

Sld 8. 13. Tworzenie stosu dla drzewa binarnego wyrażenia arytmetycznego W taki sposób pracują kompilatory w momencie obliczania wyrażeń za pośrednictwem stosu. Jedyną różnicą jest to, że nie są odkładane na stos kolejne poddrzewa, ale już obliczone fragmenty dowolnie w zasadzie skomplikowanych wyrażeń arytmetycznych.

Sld 8. 14. Odwrotna Notacja Polska - ONT Typowe wyrażenie arytmetyczne, zapisane w powszechnie używanej postaci (zwanej po polsku wrostkową), da się również przedstawić wyrażenia beznawiasowego - w tzw. Odwrotnej Notacji Polskiej (ONP, postfiksowej, zaproponował polski matematyk Jan Łukasiewicz). Zamiast pisać a op b używamy formy: ab op. Operator występuje po swoich argumentach. Operacja arytmetyczna jest łatwa do odtworzenia w postaci klasycznej, jeśli wiemy, ile operandów wymaga dany operator. Do tworzenia drzewa użyjemy stosu. ((4+7)+(3*8))*15 4 7 + 3 8 * + 15 * Analiza wyrażenia beznawiasowego odbywa się w następujący sposób: • Czytamy argumenty znak po znaku, odkładając je na stos. • W momencie pojawienia się jakiegoś operatora ze stosu zdejmowana jest odpowiednia dlań liczba argumentów - wynik operacji kładziony jest na stos jako kolejny argument.
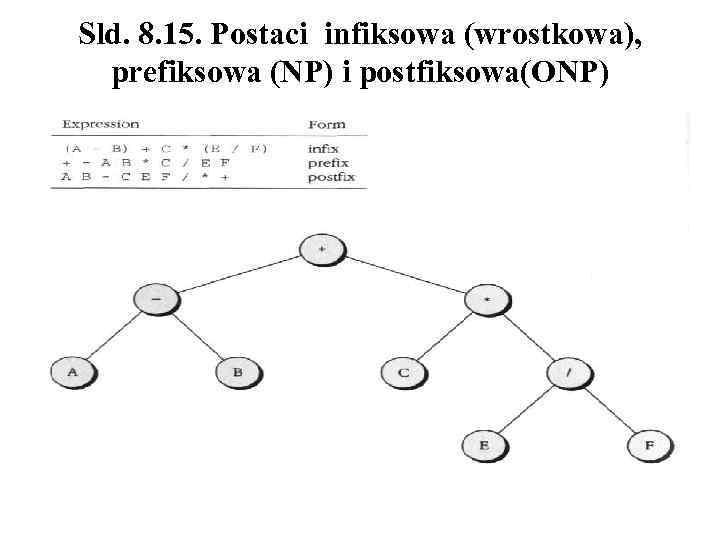
Sld. 8. 15. Postaci infiksowa (wrostkowa), prefiksowa (NP) i postfiksowa(ONP)
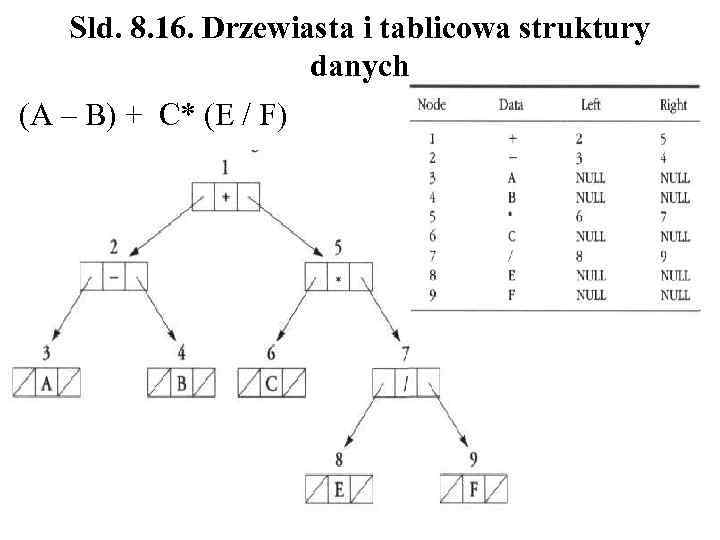
Sld. 8. 16. Drzewiasta i tablicowa struktury danych (A – B) + C* (E / F)
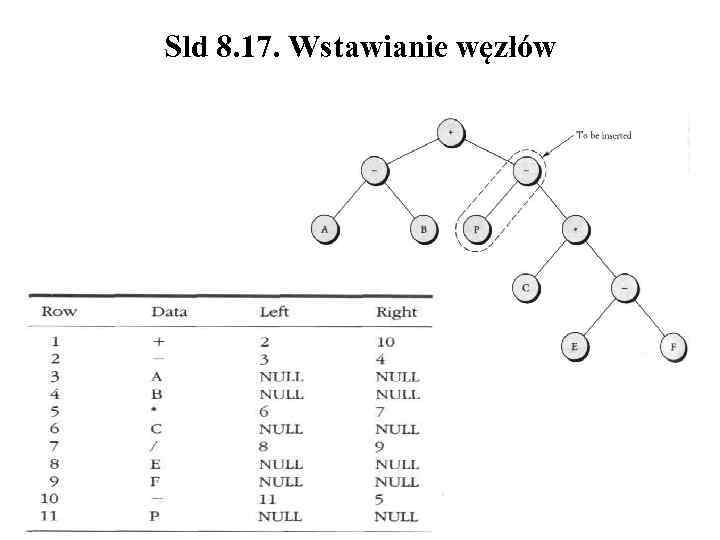
Sld 8. 17. Wstawianie węzłów
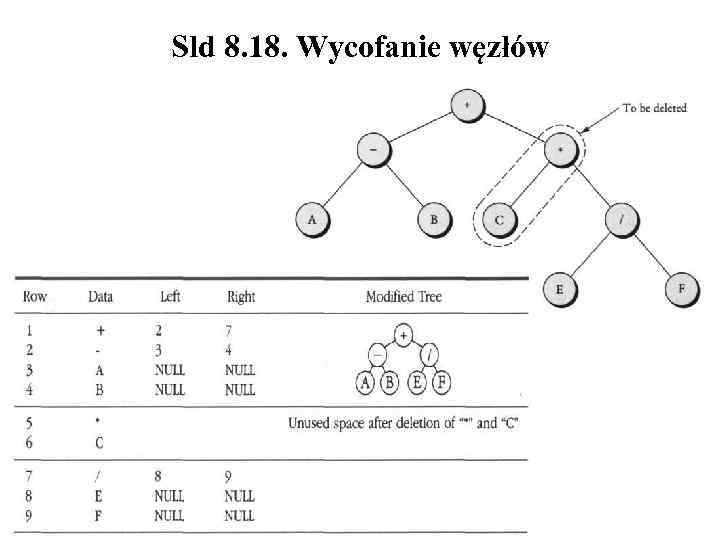
Sld 8. 18. Wycofanie węzłów
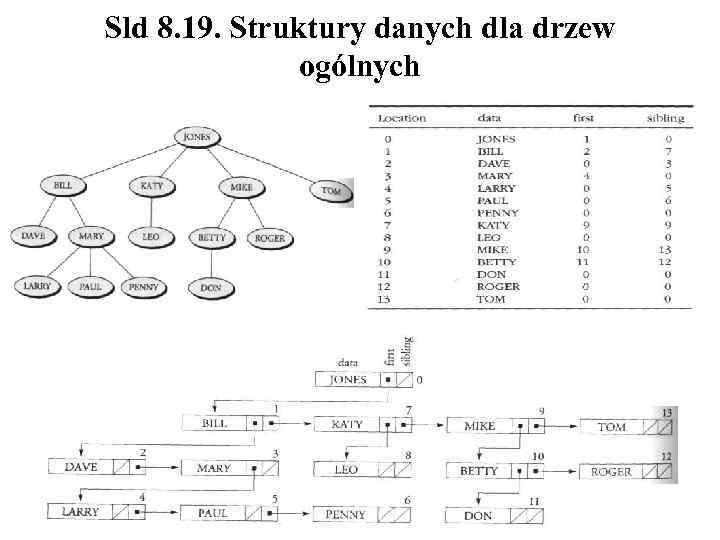
Sld 8. 19. Struktury danych dla drzew ogólnych

Sld 8. 20. Uniwersalna Struktura Słownikowa USS Z problemem weryfikacji ortograficznej (edytor tekstu) są ściśle związane następujące pytania: • jakich struktur danych używać do reprezentacji słownika? • jak zapamiętać słownik na dysku? • jak wczytać słownik „bazowy" do pamięci? • jak uaktualniać zawartość słownika?

Sld 8. 21. Uniwersalna Struktura Słownikowa - USS • USS należy do typu struktur danych, która przez swoją naturę automatycznie zapewnia kompresję danych w pamięci komputera, nie ograniczając dostępu do zapamiętanych informacji. • Idea USS opiera się na następującej obserwacji: wiele słów posiada te same rdzenie (przedrostki), różniąc się jedynie końcówkami (przyrostkami).

Sld 8. 22. Kompresja danych zaletą Uniwersalnej Struktury Słownikowej Grupa słów: KROWA, KROKUS, KROSNO, KRAWIEC, KROKODYL Z 31 znaków do zapamiętania potrzebujemy tylko 20

Sld 8. Drzewa.12.2012.ppt