Sld 3 1 Złożoność algorytmów Są dwa podstawowe

Sld 3. 1. Złożoność algorytmów Są dwa podstawowe kryteria oceny programu: • Złożoność czasowa (obliczeniowa) - czas wykonania (znowu się „ zawiesił", czy też coś liczy? !) • Złożoność pamięciowa - zajętość pamięci (już dość komunikatów typu: Insufficient memory- save your work : • Ang. Brak pamięci - zachowaj swoje dane: dość częsty komunikat w pewnym edytorze tekstów dla systemu MS-Windows. ).

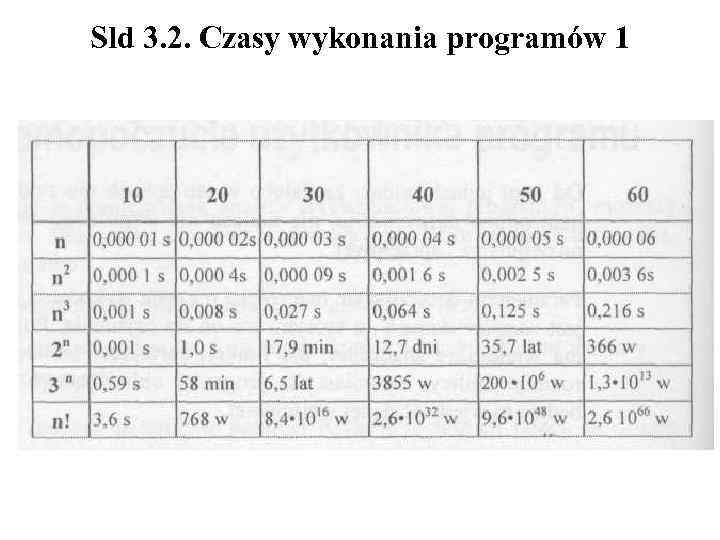Sld 3. 2. Czasy wykonania programów 1

Sld. 3. 3. Klasy złożoności • Klasa P - Problem jest problemem wielomianowym, jeśli należy do klasy O(f (n)), gdzie f (n) jest albo wielomianem, albo jest ograniczone przez wielomian (n, n 2, n 3, . . . ). Taki problem może być rozwiązany na deterministycznej maszynie Turinga za wielomianowy czas. • Klasa NP - Problem nie jest problemem wielomianowym, jeśli należy do klasy O(f (n)), gdzie f (n) nie opisuje się wielomianem, a jest eksponentą (2 n, an, n!, . . . ). Taki problem może być rozwiązany na niedeterministycznej maszynie Turinga za wielomianowy czas.

Sld 3. 3. Czasy wykonania programów 2 T NP y = n! n y=2 y = n 3 y = n 2 P y=n n

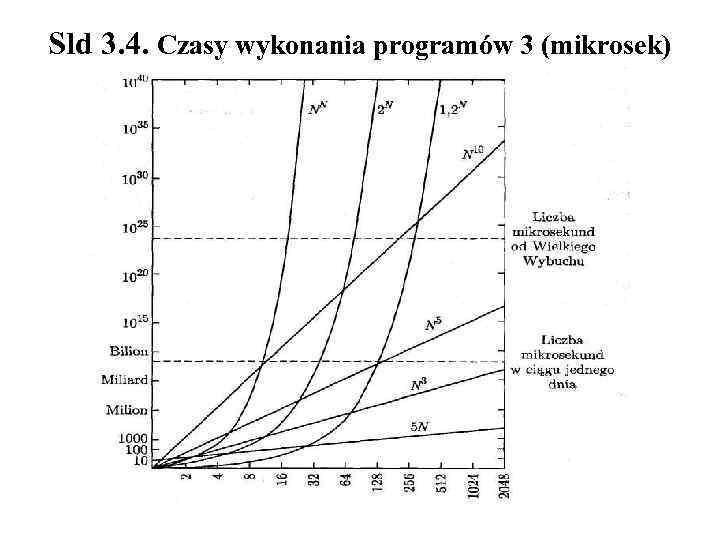Sld 3. 4. Czasy wykonania programów 3 (mikrosek)

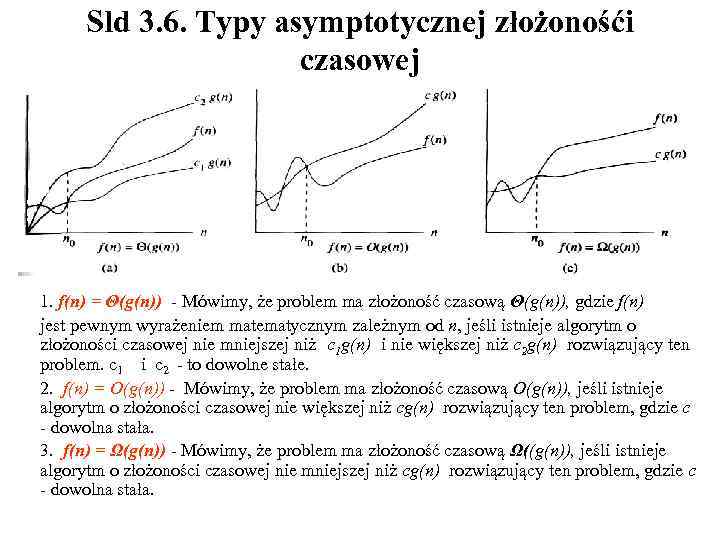Sld 3. 6. Typy asymptotycznej złożonośći czasowej 1. f(n) = Θ(g(n)) - Mówimy, że problem ma złożoność czasową Θ(g(n)), gdzie f(n) jest pewnym wyrażeniem matematycznym zależnym od n, jeśli istnieje algorytm o złożoności czasowej nie mniejszej niż c 1 g(n) i nie większej niż c 2 g(n) rozwiązujący ten problem. c 1 i c 2 - to dowolne stałe. 2. f(n) = O(g(n)) - Mówimy, że problem ma złożoność czasową O(g(n)), jeśli istnieje algorytm o złożoności czasowej nie większej niż cg(n) rozwiązujący ten problem, gdzie c - dowolna stała. 3. f(n) = Ω(g(n)) - Mówimy, że problem ma złożoność czasową Ω((g(n)), jeśli istnieje algorytm o złożoności czasowej nie mniejszej niż cg(n) rozwiązujący ten problem, gdzie c - dowolna stała.

Sld 3. 7. Złożonośći algorytmów • • log n - złożoność logarytmiczna n - złożoność liniowa n log n - złożoność liniowo-logarytmiczna n 2– złożoność kwadratowa n 3, n 4, n 5. . . – złożonośći wielomianowe n log n – złożoność podwykladnicza 2 n, a n – złożonośći wykładnicze n ! - złożoność silnia

Sld 3. 8. Przykład 1: funkcja silnia • 0 ! = 1, n! = n*(n- 1)! gdzie n ≥ 1 int silnia(int n) { if (n==O) return 1; else return n*silnia(n-l); } T(n) = tc + T(n -1), T(n-1) = tc+T(n-2), T(n-2) = tc+T(n-3), Λ T(1) = tc+T(0), T(0) = tc - czas wykonania jednej instrukcji porównania. Jeśli dodamy to stronami, to mamy: T(n) + T(n - 1)+Λ +T(0) = (n + 1)tc + T(n - 1)+Λ +T(0), co daje następującą zależność: T(n) = (n +1) tc O(n)

Sld 3. 9. Złożoność teoretyczna (klasą algorytmu) • Złożoność teoretyczna - to typ funkcji matematycznej, występującej w zależności określającej złożoność praktyczną programu, która odgrywa w niej najważniejszą rolę wpływając najsilniej na czas wykonywania programu.

Sld 3. 10. Własności złożoności teoretycznej Funkcja O jest wielkością, której można używać w równaniach matematycznych. Oto kilka własności, które mogą posłużyć do znacznego uproszczenia wyrażeń je zawierających: c· • c · O(f(n)) = O(f(n)); • O(f(n)) + O(f(n)) = O(f(n)); • O(O(f(n))) = O(f(n)); • O(f(n)) · O(g(n)) = O(f(n) · g(n)); • O(f(n) · g(n)) = f(n) · O(g(n));

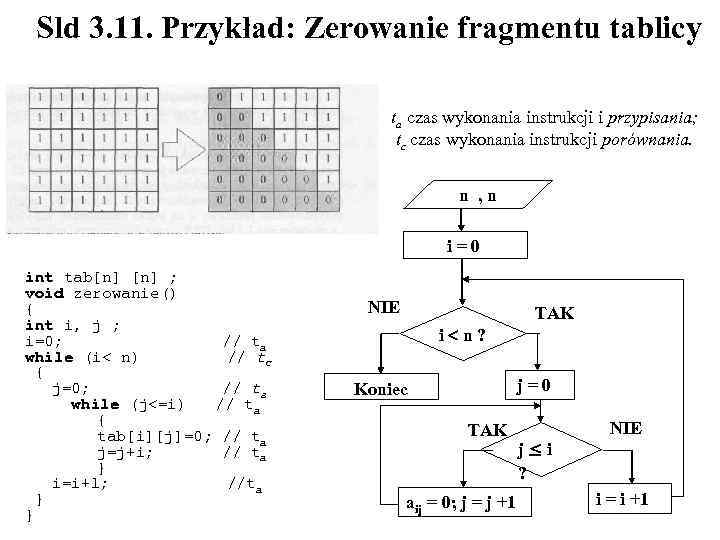Sld 3. 11. Przykład: Zerowanie fragmentu tablicy ta czas wykonania instrukcji i przypisania; tc czas wykonania instrukcji porównania. n , n i = 0 int tab[n] ; void zerowanie() { int i, j ; i=0; // ta while (i< n) // tc { j=0; // ta while (j<=i) // ta { tab[i][j]=0; // ta j=j+i; // ta } i=i+l; //ta } } NIE TAK i n ? j = 0 Koniec TAK aij = 0; j = j +1 NIE j ≤ i ? i = i +1

Sld 3. 12. Przykład: Zerowanie fragmentu tablicy 2 • Korzystając z powyższej uwagi oraz informacji zawartych w liniach komentarza możemy napisać: • Po usunięciu sumy z wewnętrznego nawiasu otrzymamy: • Przypomnijmy jeszcze użyteczny wzór na sumę szeregu liczb naturalnych od 1 do. N: • Po jego zastosowaniu w równaniu (*) otrzymamy: • Ostateczne uproszczenie wyrażenia powinno nam dać: • . . . co sugeruje od razu, że analizowany program jest klasy O(n 2).

Sld 3. 13. Wpadamy w pułapkę • Naszym problemem jest czasem nieznajomość zawartości tablicy, a ta jest potrzebna do otrzymania ostatecznego wyniku! Nie możemy zastosować funkcji matematycznej do wartości nieokreślonej. Wpadamy w pułapkę. • Nasze obliczenia doprowadziły do momentu, w którym zauważamy brak pełnej informacji o rozważanym problemie. Jedynym rozwiązaniem wydaje się zwrócenie do jakiegoś matematyka, aby ten, po przyjęciu dużej ilości założeń, przeprowadził analizę statystyczną zadania i doprowadził do ostatecznego wyniku w satysfakcjonującej nas postaci.

Sld 3. 14. Różne typy złożoności obliczeniowej Trzy podstawowe typy złożoności obliczeniowej dla przypadków: 1. najgorszego (pesymistycznego), 2. najlepszego i 3. średniego (typowego, oczekiwanego).

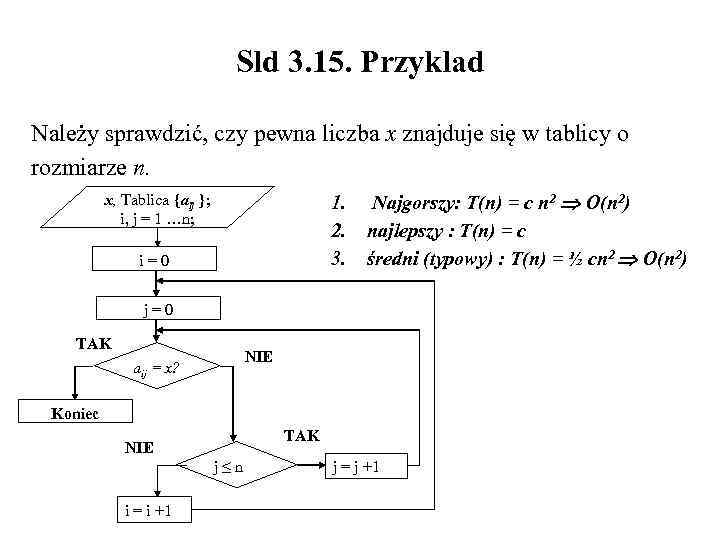Sld 3. 15. Przyklad Należy sprawdzić, czy pewna liczba x znajduje się w tablicy o rozmiarze n. x, Tablica {aij }; i, j = 1 …n; 1. 2. 3. i = 0 Najgorszy: T(n) = c n 2 O(n 2) najlepszy : T(n) = c średni (typowy) : T(n) = ½ cn 2 O(n 2) j = 0 TAK NIE aij = x? Koniec TAK NIE j ≤ n i = i +1 j = j +1

Sld 3. 16. Uprościć obliczenia złożoności obliczeniowej • W analizie programu zwracamy uwagę tylko na najbardziej „czasochłonne" operacje (np. instrukcje porównań). • Wybieramy jeden wiersz programu znajdujący się w najgłębiej położonej instrukcji iteracyjnej (pętle w pętlach, a te jeszcze w innych pętlach. . . ), a następnie obliczamy, ile razy się on wykona. Z tego wyniku dedukujemy złożoność teoretyczną.

Sld 3. 17. Analiza programów rekurencyjnych -Funkcja Ackermanna • Jest to wspaniały przykład ukazujący, jak pozornie niegroźna „z wyglądu" funkcja rekurencyjna może być kosztowna w użyciu. int A(int n, int p) { if (n==0) return 1; if ((p==0)&&(n>=l)) if (n— 1) return 2; else return n+2; if ((p>=l)&& (n>=l)) return A(A(n-1, p), p-1); }

Sld 3. 18. Problem stopu 1

Sld 3. 19. Problem stopu 1 Nie jesteśmy w stanie ustalić rzeczy tak prostej jak ta, czy program zawsze kończy działanie. Więcej, nie możemy nawet stwierdzić, czy zatrzymuje się dla wybranych danych wejściowych! Rozważmy następujący algorytm A: 1. Dopóki X ≠ 1, dopóty wykonuj X ← X - 2. Zatrzymaj się. Algorytm ten zmniejsza stopniowo wartość zmiennej wejściowej X o 2 aż dojdzie do 1. Algorytm A kończy swoje działanie tylko dla liczb nieparzystych. Zmniejszając liczbę parzystą o 2, „miniemy" jedynkę i wpadniemy w ciąg nieskończony: 0, -2, -4, -6, . . . Zagadnienie zakończenia działania wystarczy sprawdzić, czy zmienna X jest nieparzysta i w zależności od tego udzielić odpowiedzi.

Sld 3. 20. Problem stopu 2 Algorytm B: 1. Dopóki X ≠ 1, dopóty wykonuj: (a) jeśli X jest liczbą parzystą, to ustaw X ← X/2; (b) w przeciwnym razie ustaw X ← 3 X + 1. 2. Zatrzymaj się. Dla liczby 7 algorytm B wyprodukuje sekwencję: 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1. Dla dowolnej liczby całkowitej dodatniej, nawet na silnym komputerze, algorytm albo zakończy szybko swoje działanie, albo będzie produkował bez końca chaotyczny ciąg zaskakująco dużych liczb. W drugim przypadku, nie doczekawszy się zatrzymania algorytmu, będziemy zmuszeni w końcu przerwać obliczenia. Nie zauważymy też, żeby sekwencja się powtarzała, co oznaczałoby, że algorytm nigdy się nie zatrzyma. W rzeczywistości, algorytm B został już przetestowany dla wielu liczb na dużych i szybkich komputerach. Nikomu nie udało się dowieść, że dla jakiejś liczby B nie kończy działania.

Sld 3. 21. Obliczenia są nieobliczalne! • Nierozstrzygalność weryfikacji i problemu stopu stanowią właściwie tło dla znacznie głębszego rezultatu, zwanego • twierdzeniem Rice'a. Nie potrafimy zweryfikować programów, czy się zatrzymują. Z twierdzenia Rice'a wiemy, że nie możemy zadecydować o żadnej nietrywialnej własności obliczeń. Przyjmijmy, że interesuje nas własność programów spełniająca dwa warunki: (i) nie wszystkie programy mają tę własność oraz (ii)jest niezależna od składni programu, tzn. jest to własność samego algorytmu, a nie jego konkretnej implementacji. Czy program zatrzymuje się przed upływem określonego czasu, czy zawsze podaje na wyjściu liczby - ? . Z twierdzenia Rice'a wynika, że żadnej z tych własności nie da się rozstrzygnąć. Wszystkie są nierozstrzygalne.