Sld 1 1 Proces programowania 1 Tworzenie algorytmu

Sld. 1. 1. Proces programowania 1) Tworzenie algorytmu. 2) Napisanie programu (kodu). Jest tworzony tekst źródłowy programu, mający postać pliku tekstowego, wprowadzanego do komputera przy pomocy zwykłego edytora tekstowego. Generalnie efektem pracy programisty jest plik lub zespół plików opisujących w formie symbolicznej sposób zachowania się programu wynikowego. Opis ten jest kodowany w języku programowania. 3) Produkowanie kodu wykonywalnego. Kompilator dokonuje analizy poprawności i produkuje kod wykonywalny, zapisany w postaci zrozumiałej przez komputer. 4) Realizacja kodu wykonywalnego pod kontrolą systemu operacyjnego komputera.

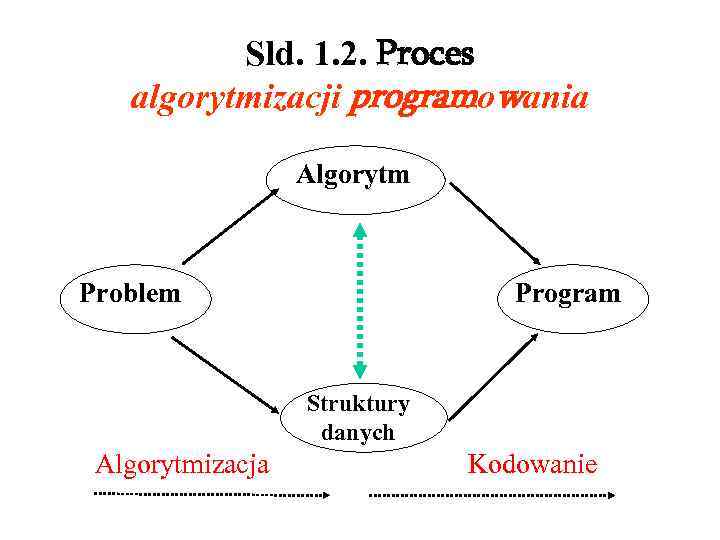Sld. 1. 2. Proces algorytmizacji programowania Algorytm Problem Program Struktury danych Algorytmizacja Kodowanie

Sld. 1. 3. Błędy i poprawność algorytmizacji programowania • Sam pomysł algorytmu, jego uważne skonstruowanie oraz zapisanie jako programu nie oznacza wcale końca. Przyjmy się następującym przykładom: • Kilka lat temu starsza pani, w wieku 107 lat, dostała komputerowo wyprodukowany list pochodzący od lokalnej instytucji edukacyjnej pewnego duńskiego okręgu administracyjnego i zawierajacy formularz rejestracyjny do pierwszej klasy szkoły podstawowej. Okazało się, że w bazie danych ludności pole „wiek" miało tylko dwie cyfry. • Zagadnienie poprawności objawiło się przy okazji tzw. problemu roku 2000, inaczej zwanego pluskwą milenijną. Jego objawy zaczną wychodzić na jaw na przełomie wieków, gdy komputery, używające dotąd dwóch cyfr do zapisywania roku, musiały działać na datach z polem roku o wartościach 00.

Sld. 1. 4. Błędy i poprawność algorytmizacji programowania W styczniu 1990 roku przestała nagle funkcjonować jedna z większych centrali telefonicznych AT&T znajdująca się w Nowym Jorku. Spowodowało to potężną awarię krajowego systemu telefonicznego AT&T. Przez Obsługiwanych przez te centralę nie dawała się nawiązać. W wyniku tego, firma straciła ponad 60 milionów dolarów, nie wspominając ogromnych strat, które dotknęły linie lotnicze, hotele, banki oraz wszystkie inne instytucje, których funkcjonowanie zależy w sposób znaczący od działania sieci telefonicznej. Awaria była spowodowana przez wadę oprogramowania, której nie zauważono, mimo stosowania złożonych metod testowania oprogramowania. Błąd znajdował się w pojedynczym programiku, to spowodował wielką lawinę błędów, która objęła cały system, czego rezultatem było unieruchomienie całej sieci.

Sld. 1. 5. Błędy i poprawność algorytmizacji programowania W czerwcu 1996 roku, na niecałą minutę po pierwszym starcie, francuska rakieta Ariane 5 uległa samozniszczeniu, co spowodowało pośrednie i bezpośrednie straty wielkości wielu bilionów dolarów oraz wielomiesięczne opóźnienie programu kosmicznego Ariane. Według komisji dochodzeniowej awaria była spowodowana przez „całkowitą utratę sterowności i informacji o wysokości w 37 sekund po odpaleniu głównego silnika". Stało się to w wyniku błędów w specyfikacji i projekcie oprogramowania systemu informacji inercyjnych. Błąd, jak się okazało, znajdował się w wierszu kodu wykonującym próbę załadowania 64 -bitowej liczby do komórki 16 -bitowej, co powodowało przepełnienie.

Sld. 1. 6. Problem wież w Hanoi Ta klasyczna łamigłówka polega na przełożeniu n krążków z drążka A na drążek C poprzez pomocniczy drążek B , przestrzegając dwóch reguł: • w jednym ruchu można przenieść tylko jeden krążek, • większy krążek nie może leżeć na mniejszym. Łamigłówkę, znaną też pod nazwą wieża Brahmy, wymyślił w 1883 r. francuski matematyk Edouard Lucas zainspirowany następującą hinduską legendą, która nawiązuje do kształtu świątyń w południowej Azji:

Sld. 1. 7. Problem wież w Hanoi • W wielkiej świątyni Brahmy, pod kopułą wyznaczającą środek świata, znajduje się płytka z brązu, na której umocowane są trzy diamentowe igły wysokie na łokieć i cienkie jak talia osy. Na jednej z tych igieł w momencie stworzenia świata umieszczono 64 krążkize szczerego złota. Największy z nich leży na. płytce z brązu, a pozostałe jeden na drugim, malejąco od największego do najmniejszego. Jest to wieża Brahmy. We dnie i w nocy bez przerwy kapłani przekładają krążki z jednej diamentowej igły na drugą, przestrzegając niewzruszonych praw Brahmy. Prawa te wymagają, aby kapłan na służbie brał tylko jeden krążek naraz i umieszczał go na jednej z igieł w ten sposób, aby nigdy nie znalazł się pod nim krążek mniejszy. Gdy 64 krążki zostaną przełożone z igły, na której znajdowały się w momencie stworzenia świata, na jedną z dwóch pozostałych igieł, wtedy wieża, świątynia i bramini rozsypią się w proch i w jednym okamgnieniu nastąpi koniec świata.

Sld. 1. 8. ZŁOŻONOŚĆ problemu wież w Hanoi 264 = 18446744073709551616 : 24 godzin x 10 kapłani = 76861433640456465 dni = 215 902 903 484 428 lat

Sld 1. 9. DEFINICJE ALGORYTMA • Skończony ciąg reguł, które aplikuje się na skończonej liczbie danych, pozwalający rozwiązywać zbliżone do siebie klasy problemów. • Zespół reguł charakterystycznych dla pewnych obliczeń lub czynności informatycznych. Termin “ALGORYTM’ pochodzi od nazwiska perskiego pisarzamatematyka Abu Ja'far Mohammed ibn Miisa al-Khowarizmi" (IX wieku n. e. ). Jego nazwisko pisane było po łacinie jako Algorismus. Jego zasługą jest dostarczenie reguł wyjaśniających krok po kroku zasady operacji arytmetycznych wykonywanych na liczbach dziesiętnych.

Sld 1. 10. Języki programowania • Języki przeznaczone do zapisu algorytmуw noszą nazwę “językуw programowania”. • Zapis algorytmu w konkretnym języku programowanianosi nazwę “programu”. • Algorytm może być wykonywany przez każdego, kto “rozumie” język, w ktуrym zapisano algorytm. Wykonawca algorytmu nie musi znać jego istoty. • Języki programowania są kompromisem pomiędzy językiem naturalnym (zrozumiałym dla człowieka), a wyrażeniami bliskimi konstrukcji komputera (bajty, bity, adresy, etc. ) • Algorytmu operują na danych. Dane (tj. informacja) reprezentują abstrakcyjny model świata rzeczywistego. Dane dostępne dla programu stanowią wybrany zbiór danych o świecie rzeczywistym. • Formy przedstawiania danych, tj struktury danych, mają istotne znacznie dla efektywności działania algorytmu.

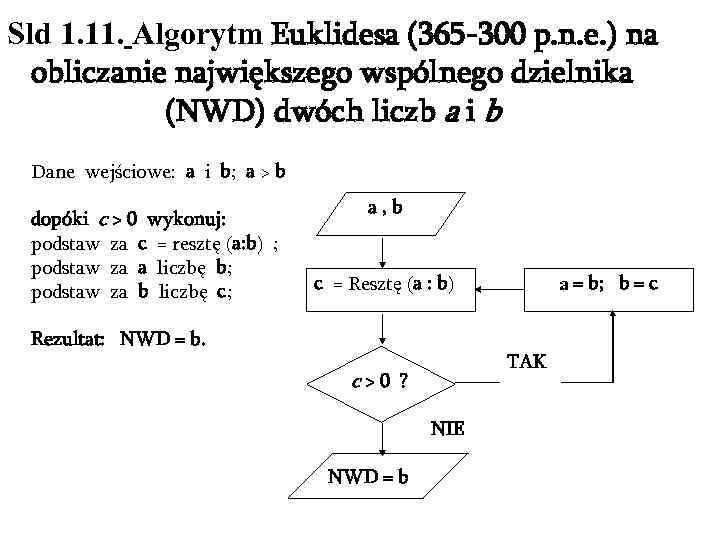Sld 1. 11. Algorytm Euklidesa (365 -300 p. n. e. ) na obliczanie największego wspólnego dzielnika (NWD) dwóch liczb a i b Dane wejściowe: a i b; a > b dopóki c > 0 wykonuj: podstaw za c = resztę (a: b) ; podstaw za a liczbę b; podstaw za b liczbę c; dopóki c > 0 wykonuj: Rezultat: NWD = b. podstaw za c = resztę (a: b) ; podstaw za a liczbę b; podstaw za b liczbę c; a , b c = Resztę (a : b) Rezultat: NWD = b. TAK c > 0 ? NIE NWD = b a = b; b = c

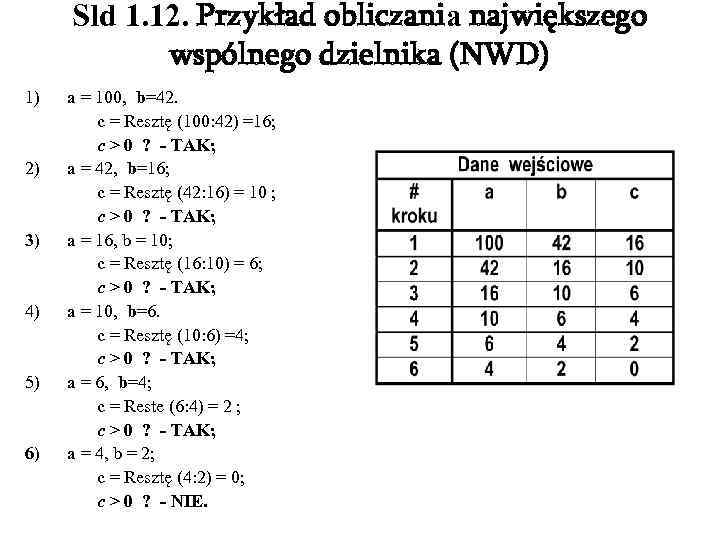Sld 1. 12. Przykład obliczania największego wspólnego dzielnika (NWD) 1) a = 100, b=42. c = Resztę (100: 42) =16; c > 0 ? - TAK; 2) a = 42, b=16; c = Resztę (42: 16) = 10 ; c > 0 ? - TAK; 3) a = 16, b = 10; c = Resztę (16: 10) = 6; c > 0 ? - TAK; 4) a = 10, b=6. c = Resztę (10: 6) =4; c > 0 ? - TAK; 5) a = 6, b=4; c = Reste (6: 4) = 2 ; c > 0 ? - TAK; 6) a = 4, b = 2; c = Resztę (4: 2) = 0; c > 0 ? - NIE.

Sld 1. 13. Algorytm Newtona y a x 2 x 4 x 3 x 1 b x x 1= a+½(b - a); y > 0; x 2= a+½(x 1 - a); y < 0; x 3= x 2+½(x 1 - x 2); y > 0; x 4= x 2+½(x 3 - x 2); y > 0; . .

Sld 1. 14. Charakterystyczny cechy algorytmów 1 Algorytm jest przepisem podającym rozwiązanie określonego problemu, mający podstawowe cechy: 1. Skończoność – zapewnienie osiągnięcie rozwiązania w skończonej liczbie krokуw. 2. Kompletność – uwzględnienie wszystkich przypadkуw podczas wykonywanie algorytmu. 3. Jednoznaczność – osiąganie zawsze identycznych wynikуw dla tych samych danych startowych.

Sld. 1. 15. Charakterystyczny cechy algorytmów 2 4) Każdy algorytm posiada dane wejściowe pochodzące z dobrze zdefiniowanego zbioru (np. algorytm Euklidesa operuje na dwóch liczbach całkowitych); 5) produkuje pewien wynik; 6) jest precyzyjnie zdefiniowany (każdy krok algorytmu musi być jednoznacznie określony).

Sld. 1. 16. Sposoby zapisu algorytmów 1. Zapis słowny. Staramy się określić sposób rozwiązania postawionego zagadnienia. 2. Lista kroków. Staramy się zapisać kolejne operacje w postaci kolejnych kroków, które należy wykonać. Budowa listy kroków obejmuje następujące elementy: • sformułowanie zagadnienia (zadanie algorytmu), • określenie zbioru danych potrzebnych do rozwiązania zagadnienia; • określenie przewidywanego wyniku (wyników), • zapis kolejnych, ponumerowanych kroków, które należy wykonać, aby przejść od punktu początkowego (dane) do końcowego (otrzymanie wyników). 3. Zapisy blokowe. Schematy blokowe i graf algorytmu.

Sld. 1. 17. Rodzaje algorytmów 1. Algorytm liniowy 2. Algorytm z rozgałęzieniem (warunkowy) 3. Algorytm z powtórzeniami (cykliczny) 4. Algorytm kombinowany (z rozgałęzieniami i powtórzeniami)

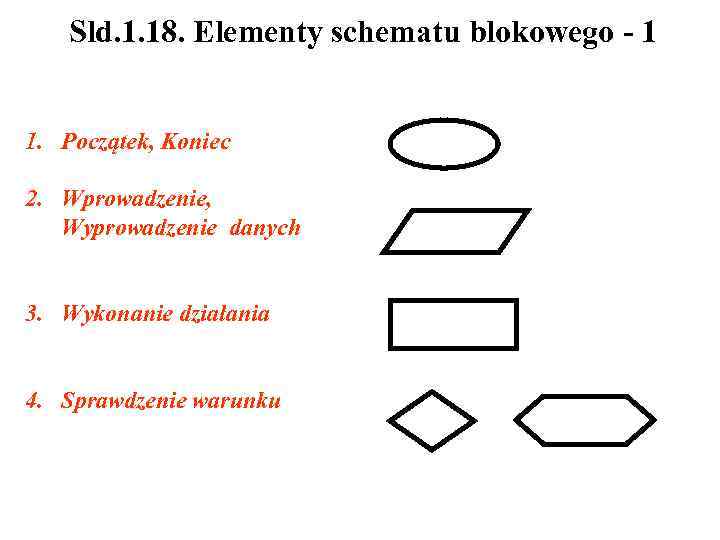Sld. 1. 18. Elementy schematu blokowego - 1 1. Początek, Koniec 2. Wprowadzenie, Wyprowadzenie danych 3. Wykonanie działania 4. Sprawdzenie warunku

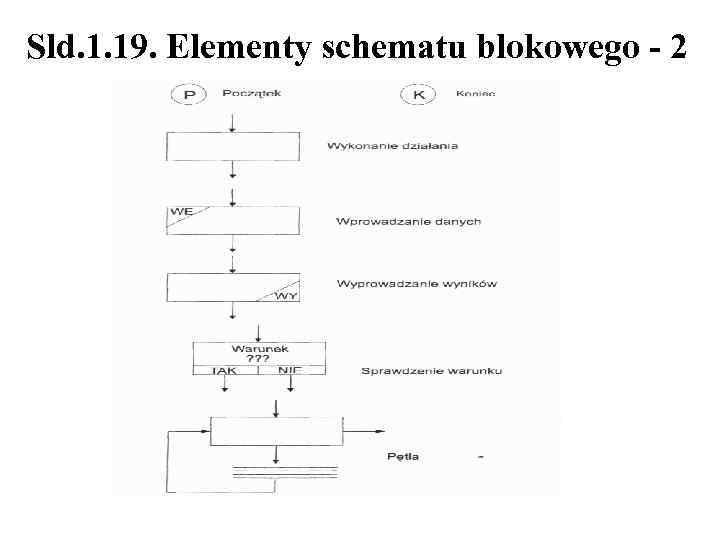Sld. 1. 19. Elementy schematu blokowego - 2

Sld. 1. 20. Elementy struktury algorytmów Każdy algorytm może być zbudowany jako kombinacja trzech podstawowych konstrukcji: 1. Sekwencji – operacje muszą być wykonywane w poprawnej kolejności, tylko jeden raz, istnieje tylko jedno wejście i jedno wyjście. 2. Selekcji (wybór) – wszystkie możliwości warunku w bloku decyzyjnym muszą być uwzględnione. 3. Cyklu (pętli) – operacje mogą być wykonywane wielokrotnie, przynajmniej jeden raz (post-check) albo wcale (pre-check), cykl nie może być nieskończony

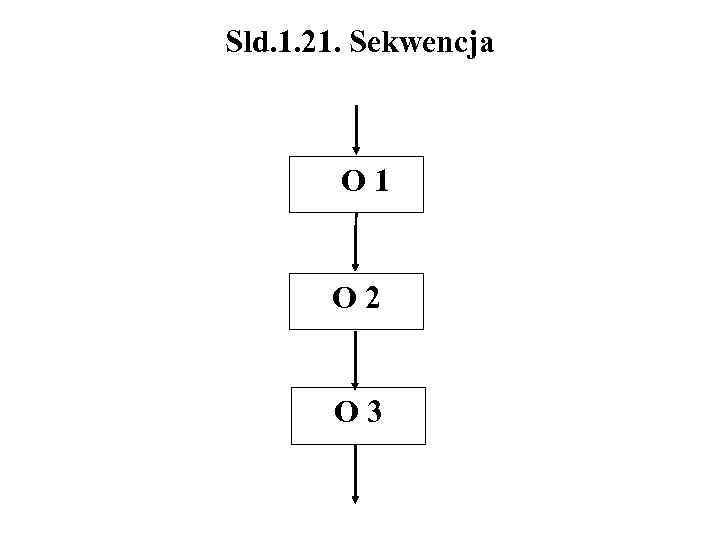Sld. 1. 21. Sekwencja O 1 O 2 O 3

Sld. 1. 20. Algorytm liniowy Najprostsza forma algorytmu, to algorytm liniowy. Ma on postać ciągu kroków, które muszą zostać bezwarunkowo wykonane jeden po drugim. Algorytm taki nie zawiera żadnych warunków ani rozgałęzień - zaczyna się od podania zestawu danych, następnie wykonywane są kolejne kroki wykonawcze, aż dochodzimy do wyniku. Przykładem może tu być dodanie lub pomnożenie dwóch liczb. 1. Sformułowanie zadania: Oblicz sumę dwóch liczb naturalnych a, b. Wynik oznacz przez S. 2. Dane wejściowe: w danymi wejściowymi są dwie liczby a, b. 3. Cel obliczeń (co ma być wynikiem): obliczenie sumy S = a + b. 4. Dodatkowe ograniczenia: na przykład warunek dla danych wejściowych, aby dane a i b były liczbami naturalnymi. Jednak konieczność sprawdzenia takiego warunku sprawia, że algorytm przestaje być liniowy.

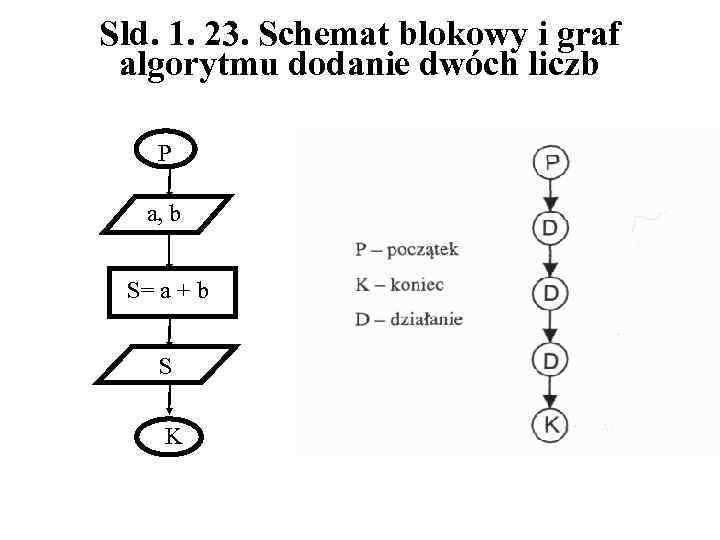Sld. 1. 23. Schemat blokowy i graf algorytmu dodanie dwóch liczb P a, b S= a + b S K

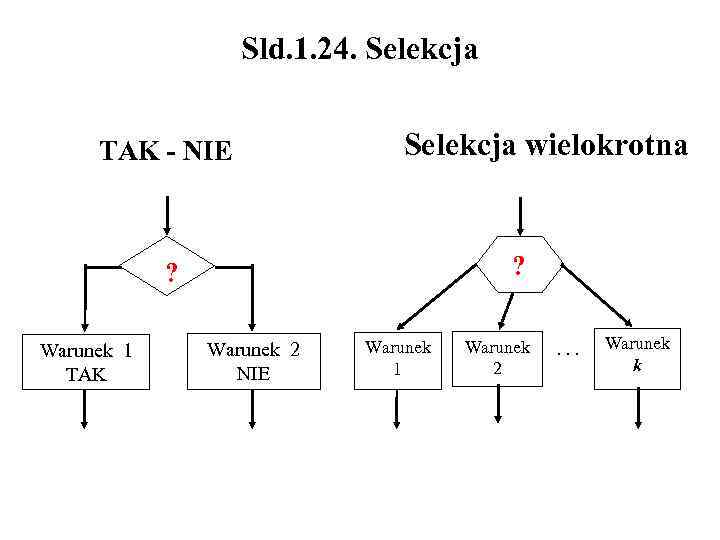Sld. 1. 24. Selekcja TAK - NIE Selekcja wielokrotna ? ? Warunek 1 TAK Warunek 2 NIE Warunek 1 Warunek . . . 2 Warunek k

Sld. 1. 25. Algorytm z rozgałęzieniem Większość algorytmów zawiera rozgałęzienia będące efektem sprawdzenia warunków. Wyrażenia warunkowe umożliwiają wykonanie zadania dla wielu wariantów danych i rozważenie różnych przypadków. Prosty przykład algorytmu z warunkiem (z rozgałęzieniem), to rozwiązanie równania liniowego. Sformułowanie zadania: Znajdź rozwiązanie równania liniowego postaci a*x + b = 0. Wynikiem jest wartość liczbowa lub stwierdzenie, dlaczego nie ma jednoznacznego rozwiązania Kolejne kroki rozwiązania będą wyglądać następująco: 1. Wprowadź dane a i b. 2. Sprawdź czy a = 0. Jeśli tak wykonaj punkt 3, jeśli nie - przejdź do punktu 4. 3. Sprawdź czy b = 0. Jeśli tak, równanie jest tożsamościowe (ma nieskończenie wiele rozwiązań), w przeciwnym przypadku równanie jest sprzeczne, czyli nie ma rozwiązania. 4. Oblicz wartość x jako -b dzielone przez a.

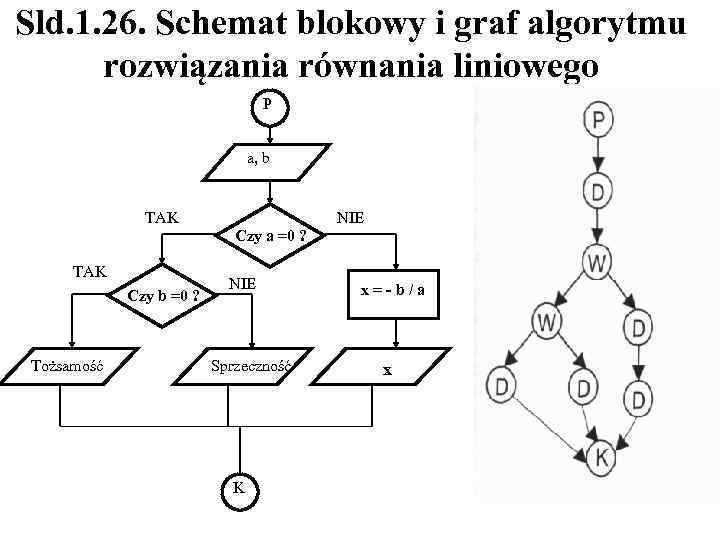Sld. 1. 26. Schemat blokowy i graf algorytmu rozwiązania równania liniowego P a, b TAK NIE Czy a =0 ? TAK Czy b =0 ? Tożsamość NIE Sprzeczność K x = - b / a x

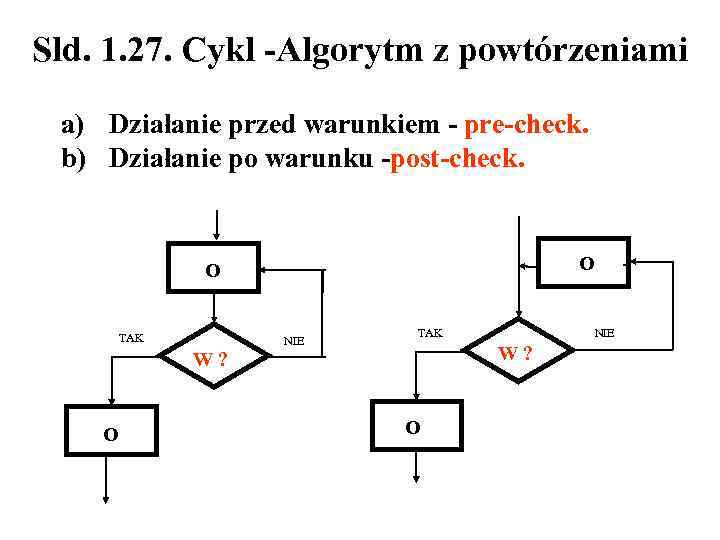Sld. 1. 27. Cykl -Algorytm z powtórzeniami a) Działanie przed warunkiem - pre-check. b) Działanie po warunku -post-check. O O TAK NIE TAK W ? O NIE O

Sld. 1. 28. Cykl - Algorytm z powtórzeniami Powtarzanie pewnych działań ma dwojaką postać: 1. liczba powtórzeń jest z góry określona (przez rozpoczęciem cyklu) lub 2. liczba powtórzeń jest nieznana (zależny od spełnienia pewnego warunku). Pierwszy przypadek najczęściej związany jest z działaniami na macierzach, drugi z obliczeniami typu iteracyjnego (iteracja to inaczej powtarzanie określonych fragmentów obliczeń w celu uzyskania właściwego wyniku). Przykładem algorytmu macierzowego jest obliczanie średniej arytmetycznej n danych liczb rzeczywistych.

Sld. 1. 29. Obliczanie średniej arytmetycznej n danych liczb rzeczywistych W algorytmie musimy opisać kolejne dodawania jako stopniowe uzupełnianie sumy do wartości końcowej. Oto kolejne kroki: 1. Wprowadź n (ile jest liczb) 2. Jeśli n = 0, zakończ działanie, gdyż nie ma żadnych liczb. 3. Ustal początkową wartość sumy S = 0 oraz licznika i = 1 4. Dodaj i-tą liczbę S = S + a, (za pierwszym razem a 1, za drugim a 2 i tak dalej) 5. Zwiększ i o jeden i = i + 1 6. Sprawdź czy i = n. Jeśli nie, wróć do punktu 4. 7. Suma została obliczona. Liczymy średnią: Średnia = S/n

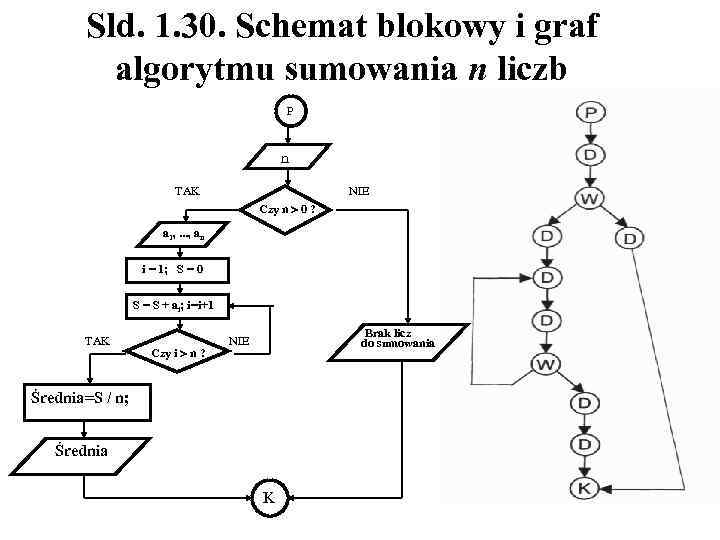Sld. 1. 30. Schemat blokowy i graf algorytmu sumowania n liczb P n TAK NIE Czy n 0 ? a 1, . . . , an i = 1; S = 0 S = S + ai; i=i+1 TAK Czy i n ? NIE Średnia=S / n; Średnia K Brak licz do sumowania

Sld. 1. 31. Programowanie strukturalne polega na budowaniu algorytmów (i programów) z użyciem tylko trzech konstrukcji: 1. sekwencji, 2. selekcji i 3. cyklu.

Sld. 1. 32. Zalety strukturalnego algorytmu ь redukcja liczby błędów ь zmniejszenie czasu tworzenia algorytmu ь łatwość podziału algorytmu na odrębne moduły ь łatwość wprowadzania modyfikacji ь większe możliwości weryfikacji algorytmu

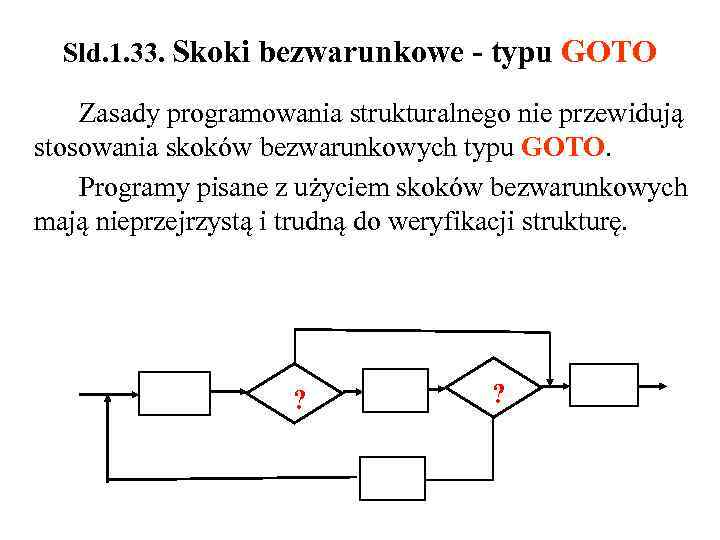Sld. 1. 33. Skoki bezwarunkowe - typu GOTO Zasady programowania strukturalnego nie przewidują stosowania skoków bezwarunkowych typu GOTO. Programy pisane z użyciem skoków bezwarunkowych mają nieprzejrzystą i trudną do weryfikacji strukturę. ?

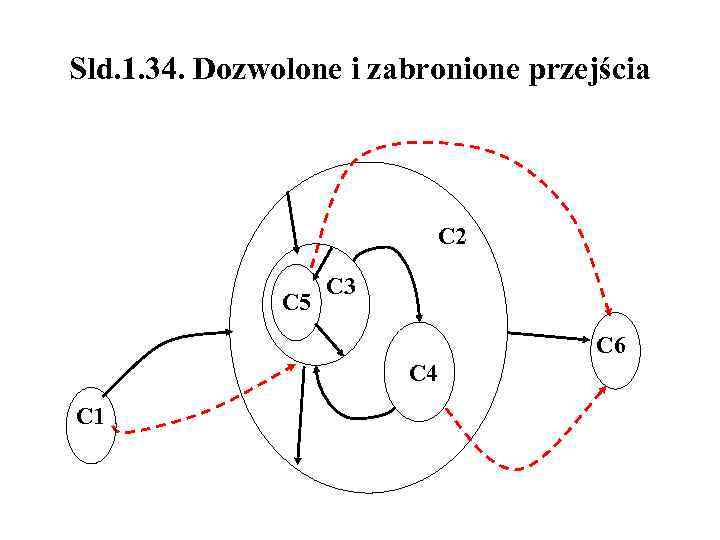Sld. 1. 34. Dozwolone i zabronione przejścia C 2 C 5 C 3 C 6 C 4 C 1

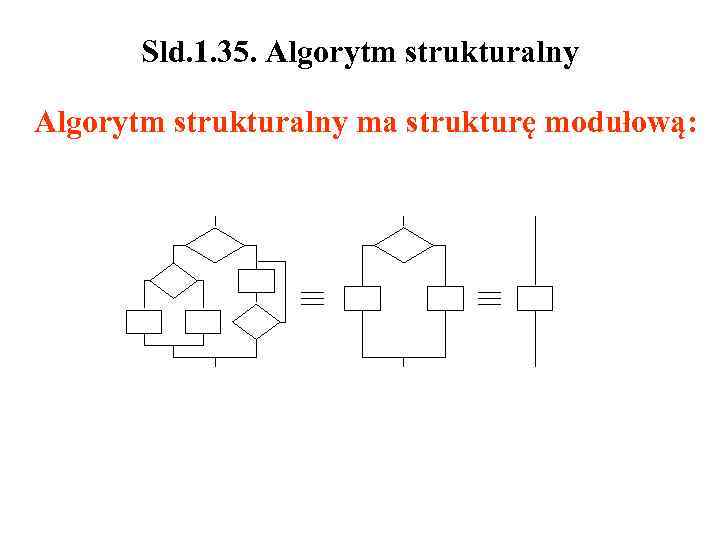Sld. 1. 35. Algorytm strukturalny ma strukturę modułową:

Sld. 1. 36. Grafy algorytmów • • Graf składa się z węzłów i gałęzi i symbolizuje przepływ informacji. W przypadku algorytmów graf można wykorzystać, aby w uproszczonej formie zilustrować liczbę różnych dróg prowadzących do określonego w zadaniu celu. Graf pozwala wykryć ścieżki, które nie prowadzą do punktu końcowego, co stanowi podstawową cechę poprawnego algorytmu. Graf ma postać uproszczonego schematu algorytmu, gdzie widać tylko węzły oraz gałęzie. Węzły symbolizują kolejne czynności Gałęzie stanowią przejścia pomiędzy węzłami. Pierwszy węzeł w grafie to węzeł startowy, ostatni - węzeł końcowy. Liczba możliwych realizacji algorytmu ma swoje odbicie w liczbie dróg, którymi można przejść między węzłami początkowym i końcowym. W klasycznym grafie występują cztery typy węzłów – początkowy, - końcowy, - węzły oznaczające działanie, - węzły z rozgałęzieniem, które stanowi wynik analizy warunku.

Sld. 1. 37. Graf algorytmu liniowego • Graf algorytmu liniowego obejmuje tylko jedną drogę od węzła początkowego do końcowego. • Każdy węzeł oznacza działanie i ma jedno wejście i jedno wyjście.

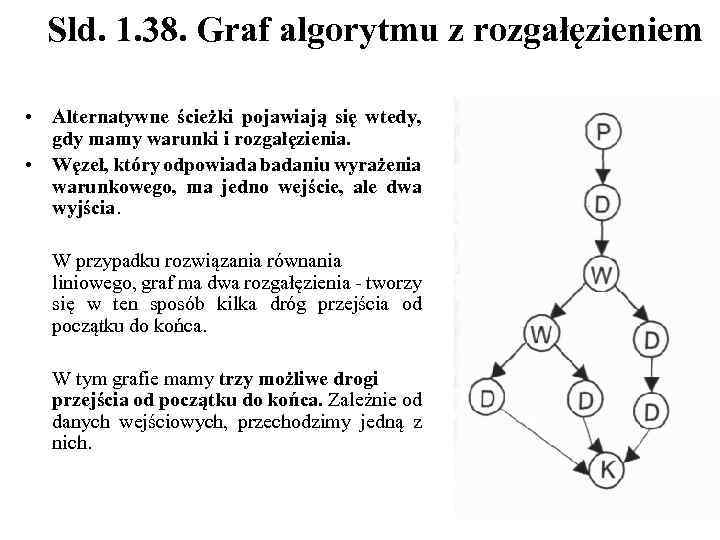Sld. 1. 38. Graf algorytmu z rozgałęzieniem • Alternatywne ścieżki pojawiają się wtedy, gdy mamy warunki i rozgałęzienia. • Węzeł, który odpowiada badaniu wyrażenia warunkowego, ma jedno wejście, ale dwa wyjścia. W przypadku rozwiązania równania liniowego, graf ma dwa rozgałęzienia - tworzy się w ten sposób kilka dróg przejścia od początku do końca. W tym grafie mamy trzy możliwe drogi przejścia od początku do końca. Zależnie od danych wejściowych, przechodzimy jedną z nich.

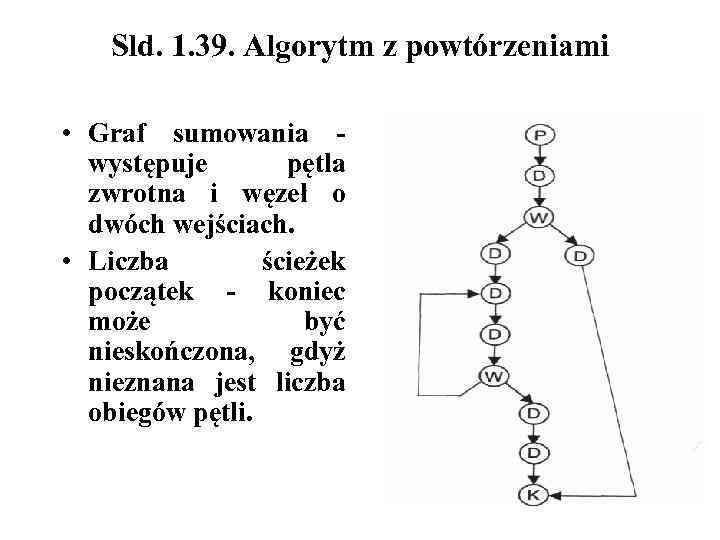Sld. 1. 39. Algorytm z powtórzeniami • Graf sumowania - występuje pętla zwrotna i węzeł o dwóch wejściach. • Liczba ścieżek początek - koniec może być nieskończona, gdyż nieznana jest liczba obiegów pętli.

Sld. 1. 40. Analiza grafu algorytmu • Graf - to schemat kontrolny służący do sprawdzenia algorytmu. • Jeśli w grafie znajdzie się ścieżka, która nie doprowadza do węzła końcowego, to mamy do czynienia z niepoprawnym grafem. Najwidoczniej jakaś sytuacja nie została przewidziana przez twórcę algorytmu podczas analizy zagadnienia i ścieżka kończy się bez doprowadzenia działania do końca. W programie przygotowanym na podstawie takiego algorytmu mamy wówczas do czynienia z przerwaniem działania i komunikatem o zaistnieniu jakiegoś błędu w działaniu (np. próby dzielenia przez zero). • Węzeł grafu może mieć dwa wejścia, jeśli ilustruje pętlę. Wtedy liczba ścieżek początek - koniec może być nieskończona, gdyż nieznana jest liczba obiegów pętli.

Sld. 1. 41. Proces koncepcji programów 1) Algorytm. • 2) Program. Jest tworzony tzw. tekst źródłowy programu, mający postać pliku tekstowego, wprowadzanego do komputera przy pomocy zwykłego edytora tekstowego. Efektem pracy programisty jest plik lub zespół plików opisujących w formie symbolicznej sposób zachowania się programu wynikowego. Opis ten jest kodowany w tzw. języku programowania. • 3) Kod wykonywalny. Kompilator dokonuje analizy poprawności i produkuje tzw. kod wykonywalny, zapisany w postaci zrozumiałej przez komputer. Plik zawierający kod wykonywalny jest następnie wykonywany pod kontrolą systemu operacyjnym komputera

Sld. 1. 42. Poziomy abstrakcji opisu algorytmu Dwie skrajne pozycje: • zbliżyć się do maszyny (język asemblera: nieczytelny dla nieprzygotowanego odbiorcy); • zbliżyć się do człowieka (opis słowny: maksymalny poziom abstrakcji zakładający poziom inteligencji odbiorcy niemożliwy aktualnie do „wbudowania" w maszynę. Problemy, nad którymi biedzą się specjaliści od sztucznej inteligencji usiłujący je rozwiązywać przy pomocy komputerów).

Sld. 1. 43. Poprawność algorytmów 1 • Jedną z możliwych ścieżek, którymi można dojść do stwierdzenia formalnej poprawności algorytmu, jest stosowanie metody niezmienników (metoda Floyda). Mając dany algorytm, możemy łatwo wyróżnić w nim pewne kluczowe punkty, w których dzieją się interesujące dla danego algorytmu rzeczy. • Ważne są 1) momenty inicjalizacji zmiennych, którymi będzie operować procedura, 2) testy zakończenia algorytmu, 3) „pętla główna". . . W każdym z tych punktów możliwe jest określenie pewnych zawsze prawdziwych warunków - tzw. niezmienników. Dowód formalnej poprawności algorytmu może być uproszczony do stwierdzenia zachowania prawdziwości niezmienników dla dowolnych danych wejściowych.

Sld. 1. 44. Poprawność algorytmów 2 Dwa typowe sposoby stosowane w praktyce dla dowodu formalnej poprawności algorytmu to: • sprawdzanie stanu punktów kontrolnych przy pomocy debuggera (odczytujemy wartości pewnych „ważnych" zmiennych i sprawdzamy, czy zachowują się „poprawnie" dla pewnych „reprezentacyjnych" danych wejściowych). • formalne udowodnienie (np. przez indukcję matematyczną) zachowania niezmienników dla dowolnych danych wejściowych.

Literatura 1. P. Wróblewski. Algorytmy. Struktury danych i techniki programowania. Helion. 2001.