Slant Asymptotes What are slant asymptotes 5

Slant Asymptotes

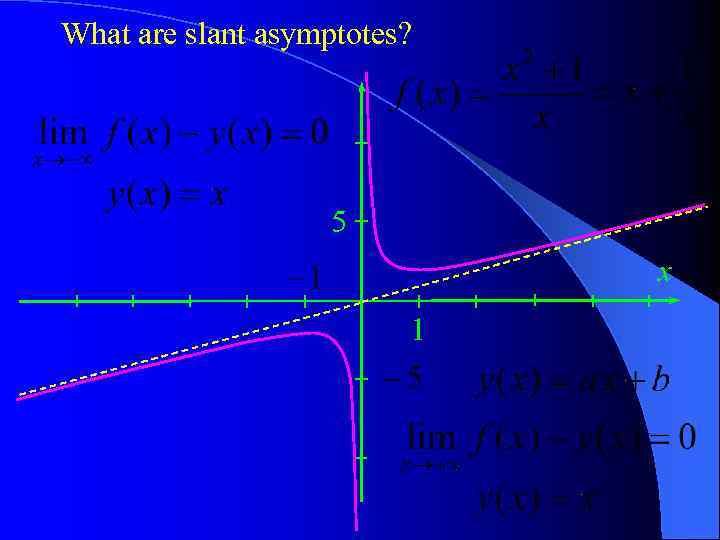What are slant asymptotes? 5 x 1

Question 1 (November 2007 Exam, Q 5). Find the asymptote of at Solution: We have to find a straight line such that Answer:

Question 2 (November 2009 Exam, Q 7). What is the asymptote of at Solution: We have to find a straight line ax + b such that Answer:

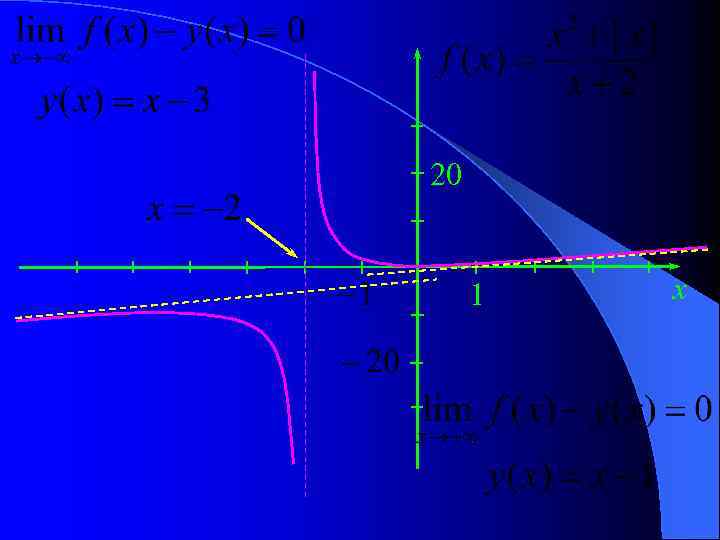20 1 x

A general property of asymptotes. If y(x) = a x + b is the asymptote for f (x) at and z(x) = c x + d is the asymptote for g(x) at then is the asymptote for at

Question 3 (October 2011 Exam, Q 19). Find the asymptotes to the graph of Solution. First we find asymptotes for To find the asymptotes we have to find constants a and b, such that and after that c and d, such that

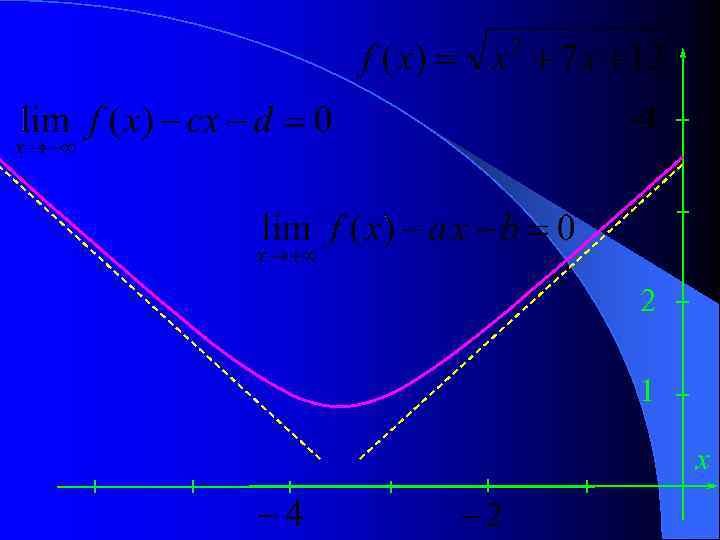2 1 x

Divide and multiply by That yields Divide numerator and denominator by x to obtain

Thus, to obtain zero limit we have to set and The function increases, as Therefore, we have to set and hence Thus, the asymptote of at is given by Using the same method we obtain the asymptote at

Hence, the asymptote of at is given by at it is given by Answer:

Calculus Ch. 3. Continuity of a function A function f (x) is continuous at a point x = a if This property is important because it helps to find limits of compound functions g(h(x)). If we know that the function g(. ) is continuous, then For example,

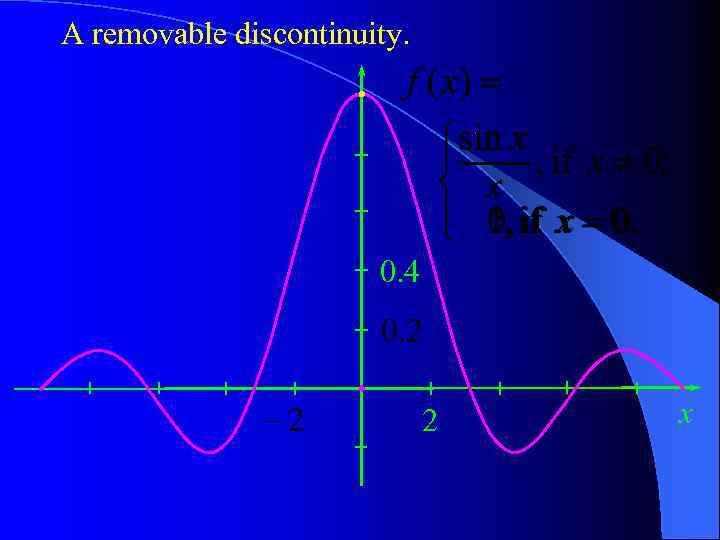A removable discontinuity. 0. 4 2 x

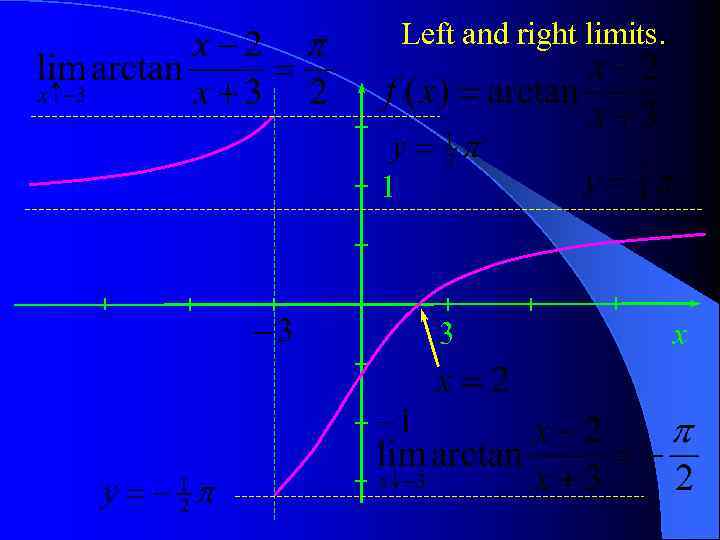Left and right limits. 1 3 x

Question 4 (November 2011 Exam, Q 3). It is known that the function f (x) is continuous for all x; Find a + b + c if Solution. Since the function is continuous, we must have Answer: a + b + c = 14.

Question 5 (October 2011 Exam, Q 23). Find t so that the function is continuous for all real x. a) -4 b) -2 c) 0 d) 1 e) 4. Solution: The first function is defined only for x < 4. The second function is defined for all x outside the interval [-2; 0].