Слайд лекция Четырехугольники без диагоналей Сущность метода Оценка

Слайд лекция «Четырехугольники без диагоналей. Сущность метода. Оценка точности цепи четырехугольников» для студентов специальности «Геодезия и картография» разработана доцентом каф. МД и Г Бесимбаевой О. Г.

План лекции 1. Сущность способа четырехугольников без диагоналей. 2. Оценка точности вычисленных сторон. 3. Оценка точности цепи четырехугольников. 4. Построение строительной сетки способом четырехугольников без диагоналей

Значительное сокращение объема измерений линий в условиях промышленных и строительных площадок обеспечивает применение метода четырехугольников без диагоналей для определения части сторон аналитическим путем. В четырехугольнике ADCB (рисунок 1) достаточно измерить углы и две стороны, образующие любой угол. Две другие стороны вычисляют по формулам, выводимым из построения DD 1||CB и DВ 1||DC.

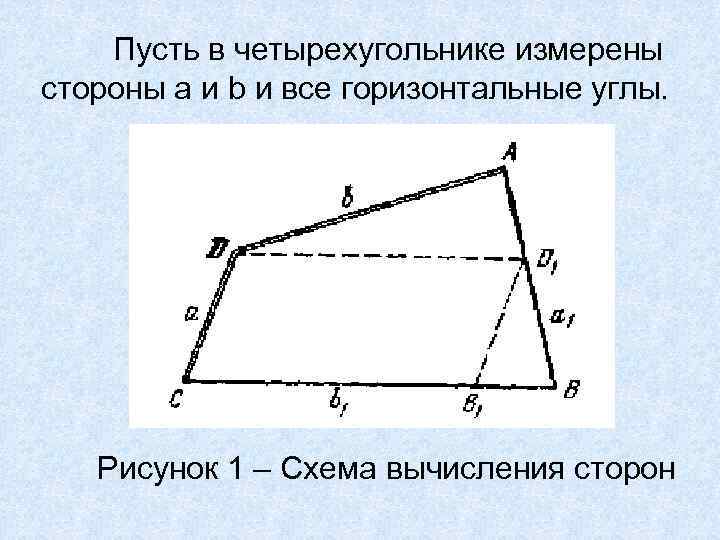
Пусть в четырехугольнике измерены стороны а и b и все горизонтальные углы. Рисунок 1 – Схема вычисления сторон

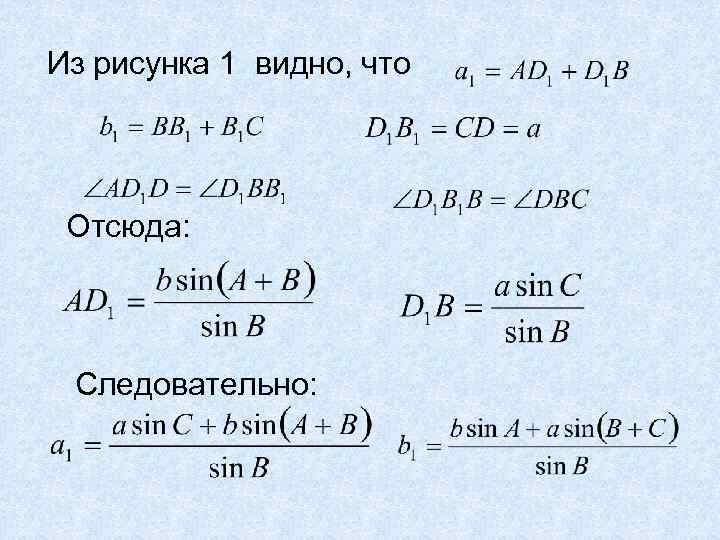
Из рисунка 1 видно, что Отсюда: Следовательно:

Для вычисления сторон цепи четырехугольников (рисунок 2), в которых измерены все углы, достаточно в каждом четырехугольнике, кроме начального, измерить только одну сторону (показана двойной линией) и в качестве второй стороны использовать вычисленную из предыдущего четырехугольника.

Рисунок 2 Цепь четырехугольников без диагоналей В цепи из n четырехугольников достаточно измерить n+1 сторону. Так, в цепи на рисунке 2 при измерении шести сторон десять определяют аналитически.

В сети четырехугольников соотношение вычисляемых и измеряемых сторон еще выгоднее. Для сети на рисунке 3 нужно измерить только восемь сторон для вычисления 24. Рисунок 3 Сеть четырехугольников

Оценка точности вычисленных сторон Обозначим средние квадратические погрешности при равноточном измерении углов в четырехугольнике и предварительном их уравнивании за условие фигуры (см. рисунок 1) mβ погрешности измерения сторон mα и mb, погрешности вычисленных сторон ma 1 и mb 1.

Погрешности вычисленных сторон для прямоугольных четырехугольников будут равны: При этом относительные погрешности вычисленных сторон будут равны

Погрешности вычисленных сторон для квадрата будут равны Средняя квадратическая погрешность вычисленного дирекционного угла стороны а 1 четырехугольника определяется по формуле где m. Ta погрешность дирекционного угла исходной стороны а.

На точность определения вычисляемых сторон влияет форма четырехугольника. Учитывая только погрешности измерения углов, из этих формул получаем для ромба (а = a 1 = b =b 1 ; A +В = 180°; С +D = 180°) погрешность вычисленной стороны ma 1

Значение угла A, при котором mα 1 = min, получим, приравняв нулю частную производную от mα 1 по А; после соответствующих преобразований получим: Так как равенство возможно при A =90=270.

Следовательно, наивыгоднейшая форма четырехугольника это квадрат, обеспечивающий минимальные погреш ности в определяемых сторонах и наибольший продвиг в сетях из четырехугольников без диагоналей. При помощи коэффициента в формуле можно определить снижение точности вычисления сторон в четырехугольнике в зависимости от величины его углов (таблица 1).

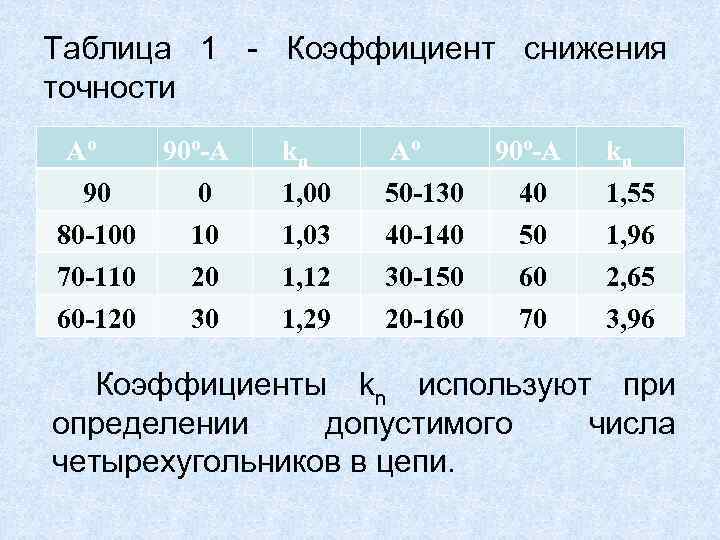
Таблица 1 Коэффициент снижения точности Аº 90 80 -100 70 -110 60 -120 90º-А 0 10 20 30 kn 1, 00 Аº 50 -130 90º-А 40 kn 1, 55 1, 03 1, 12 1, 29 40 -140 30 -150 20 -160 50 60 70 1, 96 2, 65 3, 96 Коэффициенты kn используют при определении допустимого числа четырехугольников в цепи.

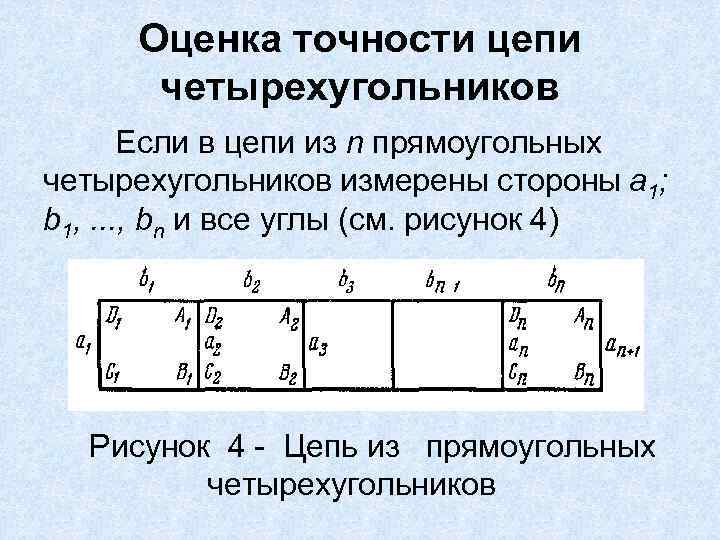
Оценка точности цепи четырехугольников Если в цепи из n прямоугольных четырехугольников измерены стороны а 1; b 1, . . . , bn и все углы (см. рисунок 4) Рисунок 4 Цепь из прямоугольных четырехугольников

Погрешность определения стороны аn+1 Относительная погрешность стороны аn+1 Для цепи, состоящей из четырехугольников, близких к квадратам

По формулам можно вычислить погрешности любой из промежуточных сторон цепи. Необходимо оп ределить допустимое число прямоугольных четырехугольников в цепи n, при котором будет выдержана заданная точность стороны аn,

Для цепи, состоящей из четырехугольников произвольной формы, n, вычисленное по ранее приведенной формуле, необходимо разделить на сумму коэффициентов снижения точности выбранную из таблицы 1.

Построение строительной сетки способом четырехугольников без диагоналей Применение способа четырех угольников без диагоналей позволяет построить строительную сетку в любых производственных условиях, на открытых и застроенных площадках, при минимальной затрате времени на полевые и камеральные работы.

Построение сетей из четырехугольников без диагоналей с применением светодальномеров производят в такой последовательности 1. Составляют проект сети с привязкой ее к исходным пунктам. 2. Закрепляют пункты постоянными и временными знаками.

3. Между исходными пунктами (триангуляции или полигонометрии старших разрядов) прокладывают ходы светодальномерной полигонометрии необходимой точности по направлениям, разделяющим проектируемую сеть на секции, состоящие из 12— 25 четырехугольников (рисунок 5). Таким образом, ходы прокладывают только по границам (периметрам) секции.

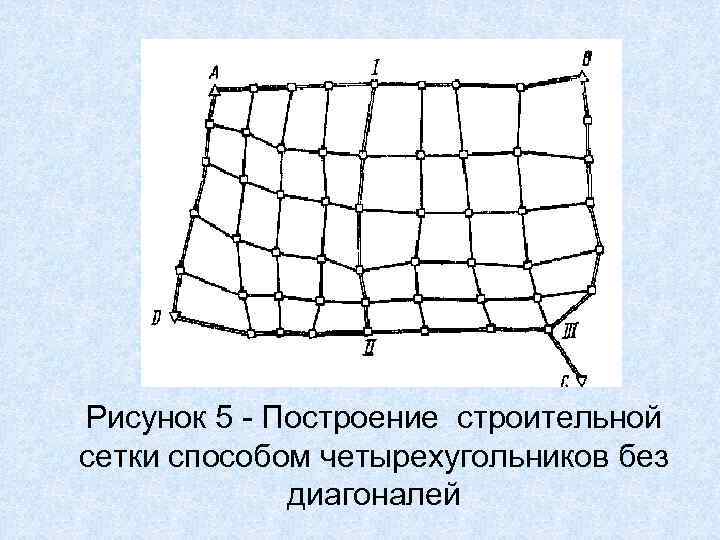
Рисунок 5 Построение строительной сетки способом четырехугольников без диагоналей

4. Измеряют горизонтальные углы на пунктах сети внутри секций (между четырьмя направлениями на каждом пункте). По мере замыкания полигонов должна составляться схема сети, в которой записывают измеренные углы, для подсчета по ней невязок в полигонах. Подробные схемы следует также составлять и по основным ходам, прокладываемым на границах секций.

5. Определяют высоты пунктов сети. Высоты пунктов полигонометрии определяют нивелированием с точностью, предусмотренной проектом работ. 6. Производят камеральную обработку полигонометрических ходов и получают уравненные плоские координаты пунктов ходов, стороны которых являются исходными для вычислений длин сторон сети четырехугольников.

7. Горизонтальные углы, измеренные на пунктах сети, уравнивают внутри секций совместно по методу полигонов В. В. Попова (как свободную сеть). 8. Вычисляют длины сторон сети, используя в качестве исходных не уравненные длины сторон, определенные в основных ходах полигонометрии.

Вначале последовательно вычис ляют стороны цепи четырехугольников, примыкающих к границе секции, начиная с первого четырехугольника цепи, в котором определены длины двух сторон а 1 и b 1. Связующая сторона a 2, вычисленная в первом четырехугольнике, используется в качестве исходной во втором и т. д. Одновременно вычисляют проме жуточные стороны.

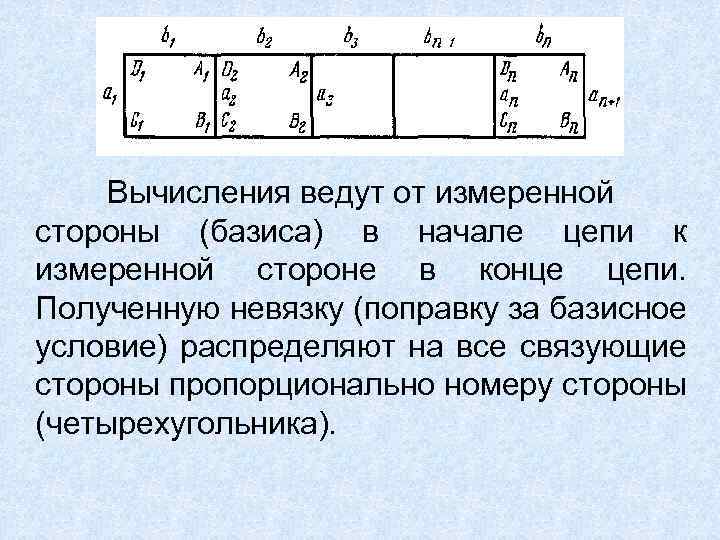
Вычисления ведут от измеренной стороны (базиса) в начале цепи к измеренной стороне в конце цепи. Полученную невязку (поправку за базисное условие) распределяют на все связующие стороны пропорционально номеру стороны (четырехугольника).

После решения последнего четырехугольника в цепи вычисляют свободный член базисного условия — невязку цепи по формуле После вычисления сторон четырехугольников в первой цепи вычисляют в этой же последовательности стороны второй цепи.

При этом промежуточные стороны b 1, b 2, . . . , bn, полученные при решении одной цепи четырехугольников, в свою очередь, используют как исходные при решении второй цепи и т. д. После решения последней цепи четырехугольников в секции вычисляют невязки промежуточных сторон по формуле

В вычисленные значения сторон вводят предварительные поправки по формулам где n — число связующих сторон в цепи; N — номер стороны; siвыч — вычисленная сторона; siизм, — измеренная сторона.

9. Вычисляют дирекционные углы сторон сети. В большинстве случаев уравненные дирекционные углы четырехугольников достаточно вычислить приближенным способом в такой последовательности: 1) Определить дирекционные углы сторон первых цепей четырехугольников, примыкающих к основным полигонометрическим ходам, по формуле

2) Так как дирекционный угол каждой связующей стороны вычисляют дважды (из смежных четырехугольников), то окончательное значение его можно получить как среднее арифметическое по формуле 3) Дирекционные углы проме жуточных сторон четырехугольников вычисляют аналогично.

Вычисления производят на схеме, в которую выписывают: а)исходные дирекционные углы (красной тушью); б)уравненные углы четырехугольников (черной тушью). По мере вычисления дирекционных углов их значения выписывают на схему внутри тех четырехугольников, в которых они вычислены. Средние значения дирекционных углов выписывают красной тушью.

10. Вычисляют приращения между пунктами сети и совместно уравновешивают их внутри секций. Приращения координат по сторонам четырехугольников вычисляют по обычным формулам. Одновременно подсчитывают свободные члены координатных условий в каждом замкнутом четырехугольнике.

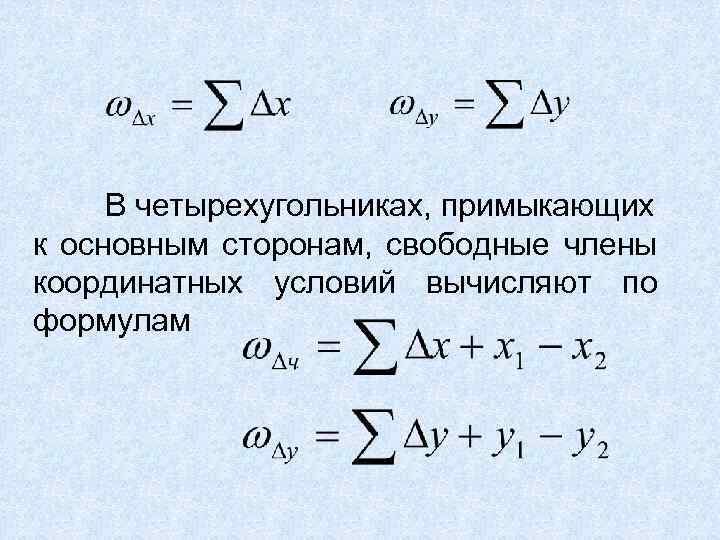
В четырехугольниках, примыкающих к основным сторонам, свободные члены координатных условий вычисляют по формулам

11. Вычисляют рабочие координаты пунктов сети по методу узлов В. В. Попова. 12. Высоты пунктов сети вычисляют также методом узлов В. В. Попова по способу последовательных приближений (поразрядно). В отдельных случаях требуется более высокая точность координат пунктов полигонометрических сетей. Для этого необходимо выполнить строгое уравнивание пунктов сети, расположенных внутри секций.

Способ четырехугольников, особенно с применением электрооптических светодальномеров, в значительной степени облегчает труд геодезистов, выполняющих работы по построению геодезической основы.

Контрольные задания для СРС 1. Формулы вычисления сторон. 2. Погрешности вычисленных сторон ma 1 и mb 1. 3. Коэффициент снижения точности. 4. Допустимое число прямоугольных четырехугольников в цепи. 5. Вычисление свободного члена базисного условия. 6. Вычисление свободных членов координатных условий.

Рекомендуемая литература: 1 Сундуков Я. А. Геодезические работы при возведении крупных промышленных сооружений и высотных зданий. М. , Недра, 1980 343 с. Стр. 41 48. 2 Андреева Ф. В. и др. Геодезическое обеспечение жилищно гражданского и промышленного строительства. М. Недра, 1988 270 с. Стр. 42 51.