Скрещивающиеся прямые 10 класс Задача 1

Скрещивающиеся прямые. 10 класс

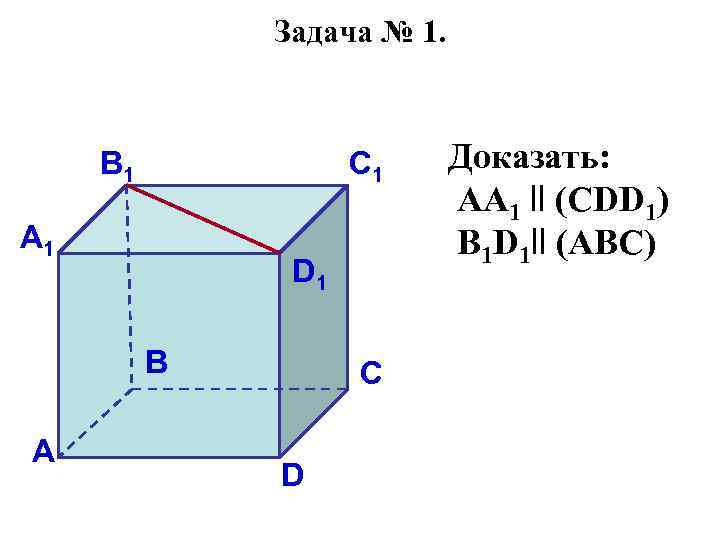Задача № 1. B 1 C 1 A 1 D 1 B A C D Доказать: АА 1 ll (CDD 1) B 1 D 1 ll (ABC)

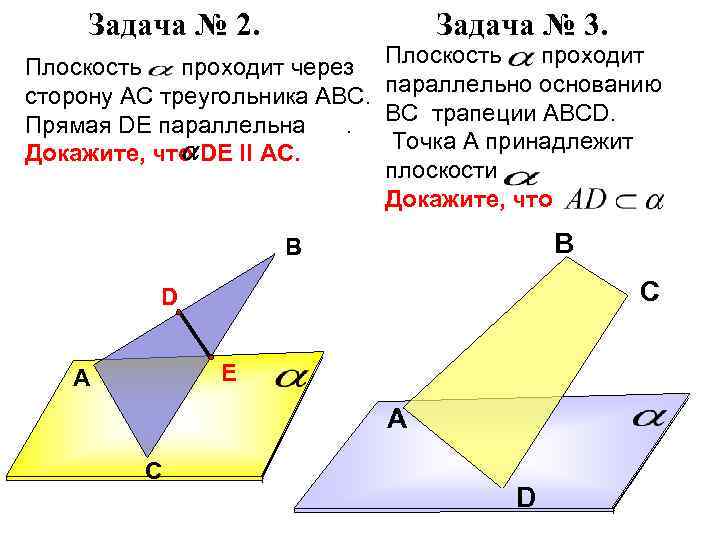Задача № 2. Задача № 3. Плоскость проходит через сторону АС треугольника АВС. Прямая DE параллельна. a Докажите, что DE II АС. Плоскость проходит параллельно основанию ВС трапеции АВСD. Точка А принадлежит плоскости. Докажите, что В В С D E A A С D

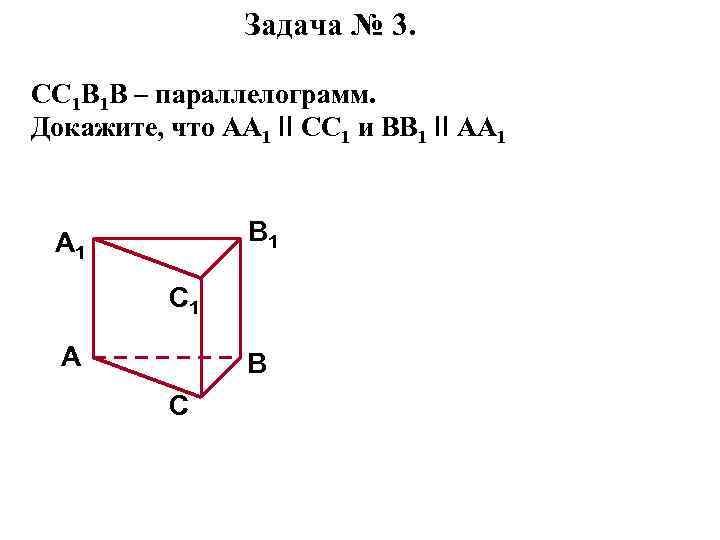Задача № 3. CС 1 B 1 B – параллелограмм. Докажите, что АА 1 II СС 1 и ВВ 1 II АА 1 B 1 A 1 C 1 A B C

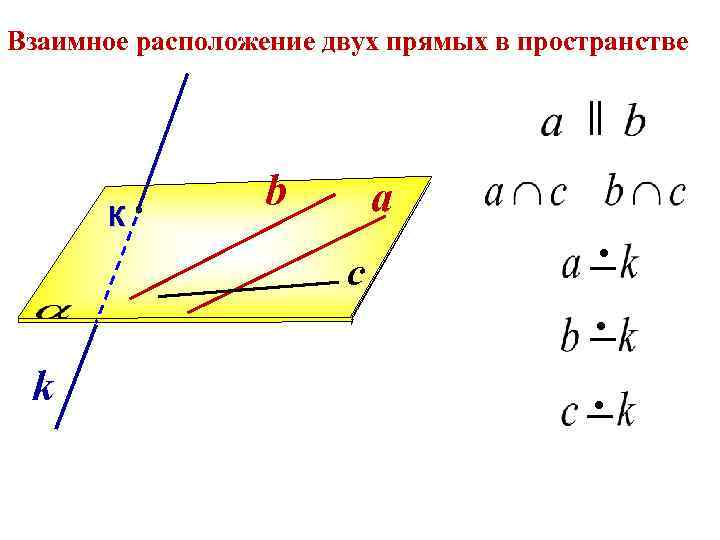Взаимное расположение двух прямых в пространстве II К b a с k ● _ _ ●

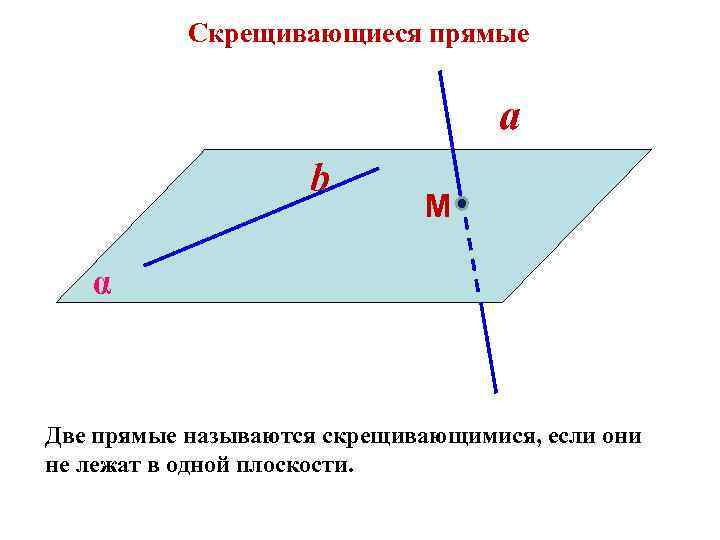Скрещивающиеся прямые a b М α Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

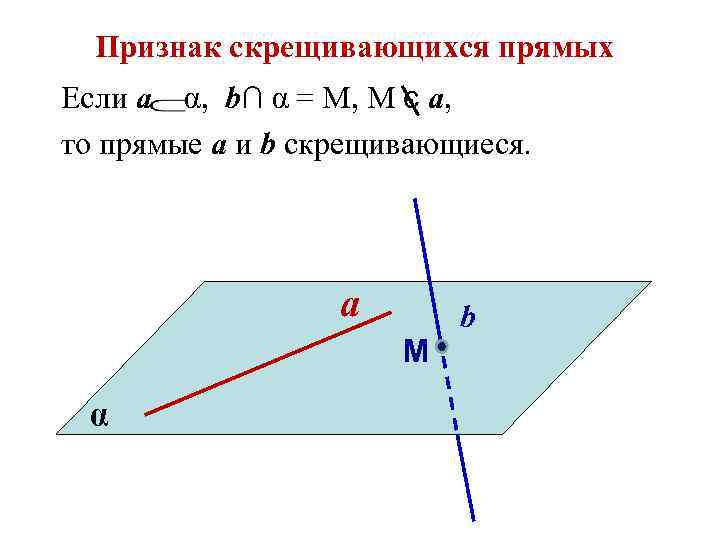Признак скрещивающихся прямых Если а α, b∩ α = M, M є a, то прямые a и b скрещивающиеся. a M α b

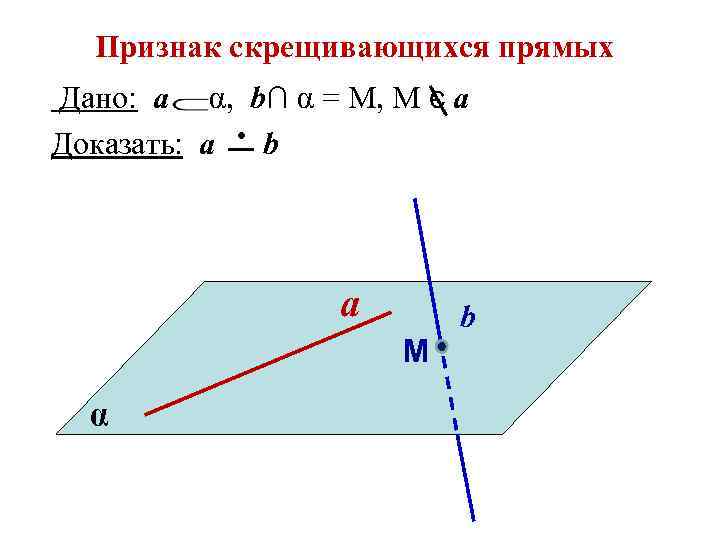Признак скрещивающихся прямых Дано: а α, b∩ α = M, M є a ● _b Доказать: a a M α b

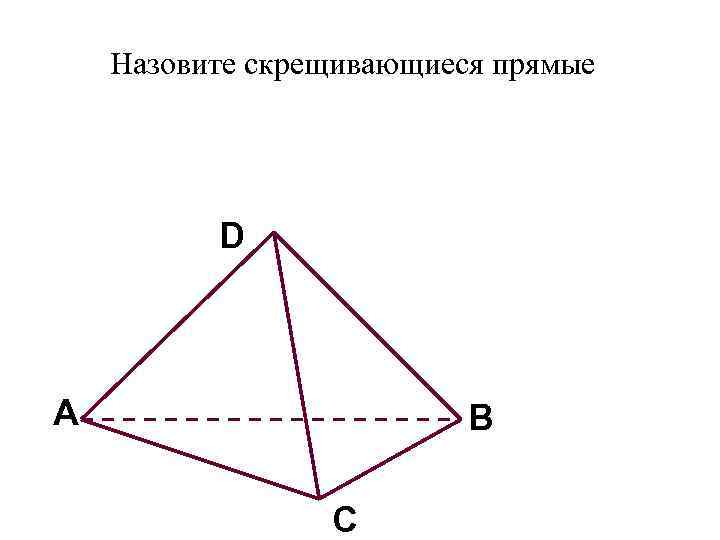Назовите скрещивающиеся прямые D A B C

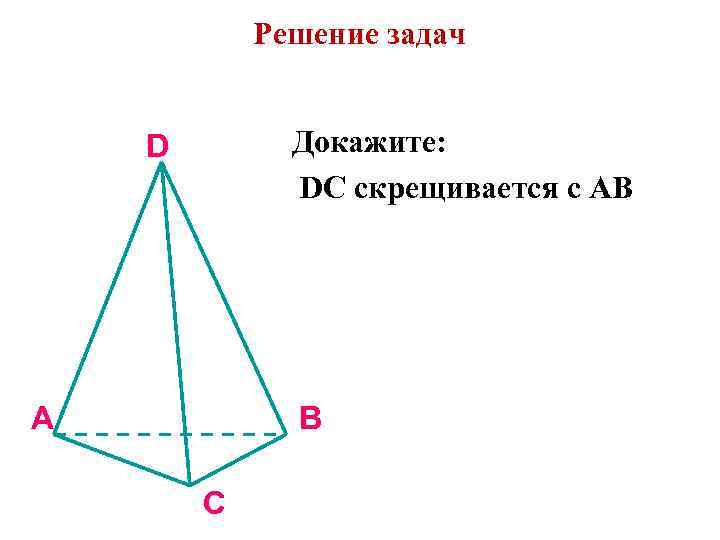Решение задач Докажите: DC скрещивается с AB D A B C

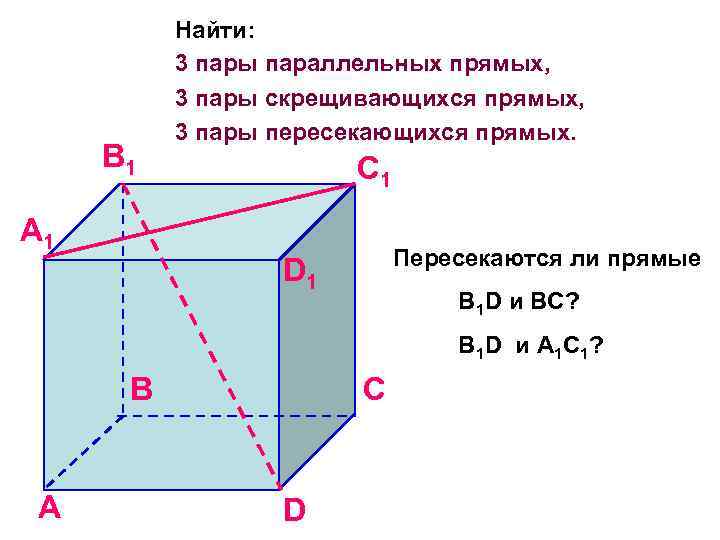B 1 A 1 Найти: 3 пары параллельных прямых, 3 пары скрещивающихся прямых, 3 пары пересекающихся прямых. C 1 Пересекаются ли прямые D 1 B 1 D и BC? B 1 D и A 1 C 1? B A C D

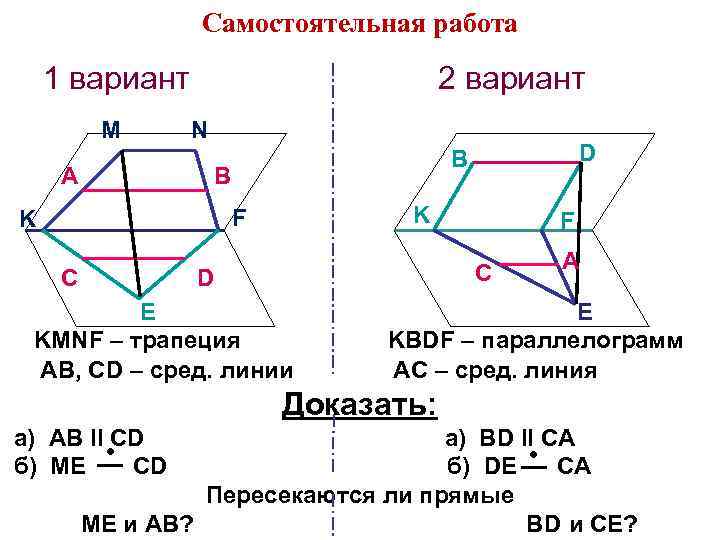Самостоятельная работа 1 вариант M A 2 вариант N B K F K C E KMNF – трапеция АВ, СD – сред. линии _ F A C D а) AB ll ● CD б) ME CD D B E KBDF – параллелограмм АС – сред. линия Доказать: _ а) BD ll CA ● б) DE CA Пересекаются ли прямые ME и AB? BD и CЕ?

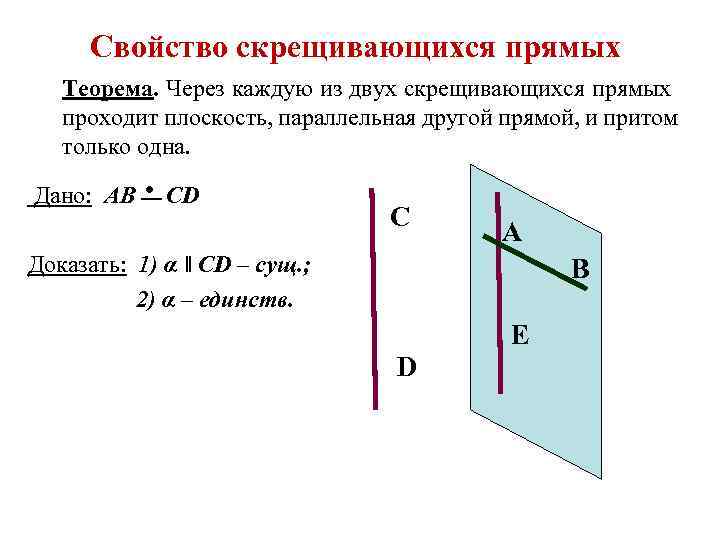Свойство скрещивающихся прямых Теорема. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна. ● Дано: AB _ CD С A Доказать: 1) α ǁ CD – cущ. ; 2) α – единств. В Е D

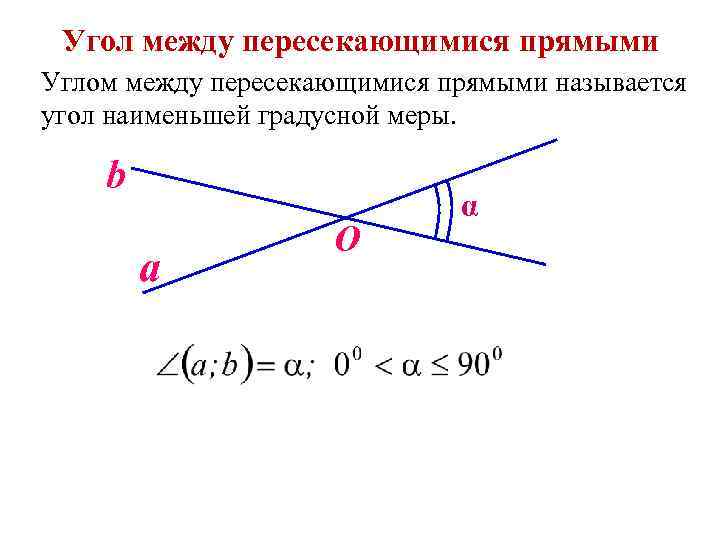Угол между пересекающимися прямыми Углом между пересекающимися прямыми называется угол наименьшей градусной меры. b a O α

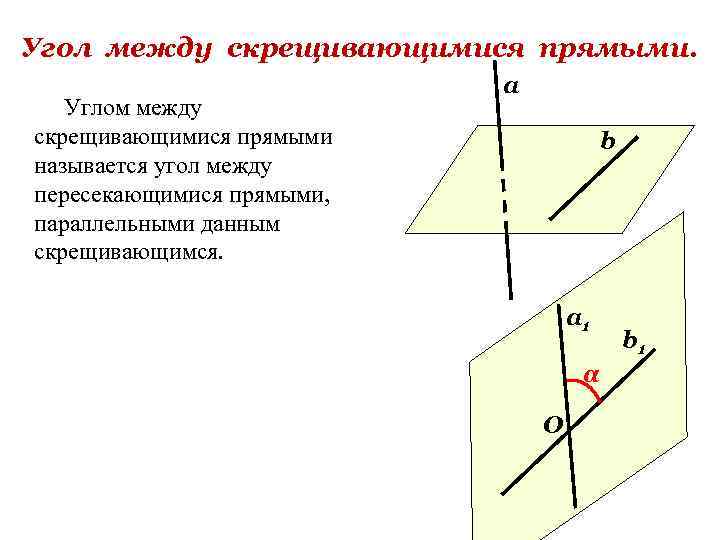Угол между скрещивающимися прямыми. Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, параллельными данным скрещивающимся. а b a 1 α О b 1

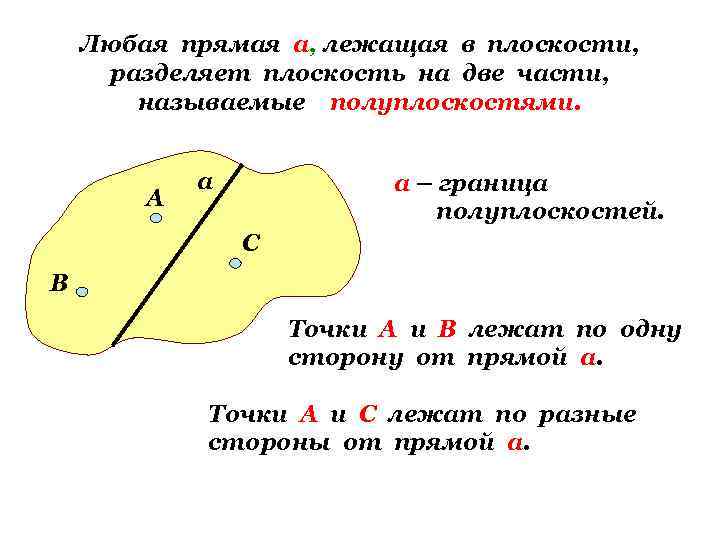Любая прямая а, лежащая в плоскости, разделяет плоскость на две части, называемые полуплоскостями. А а а – граница полуплоскостей. С В Точки А и В лежат по одну сторону от прямой а. Точки А и С лежат по разные стороны от прямой а.

Работа с учебником п. 8 стр. 17. Два луча называются сонаправленными, если: 1) они II и лежат в одной полуплоскости; 2) они совпадают; 3) один из них содержит другой;

Теорема об углах с сонаправленными сторонами Если стороны двух углов соответственно сонаправлены, то такие углы равны. Дано: с сонаправленными сторонами. А О Доказать: О 1 В В 1 А 1

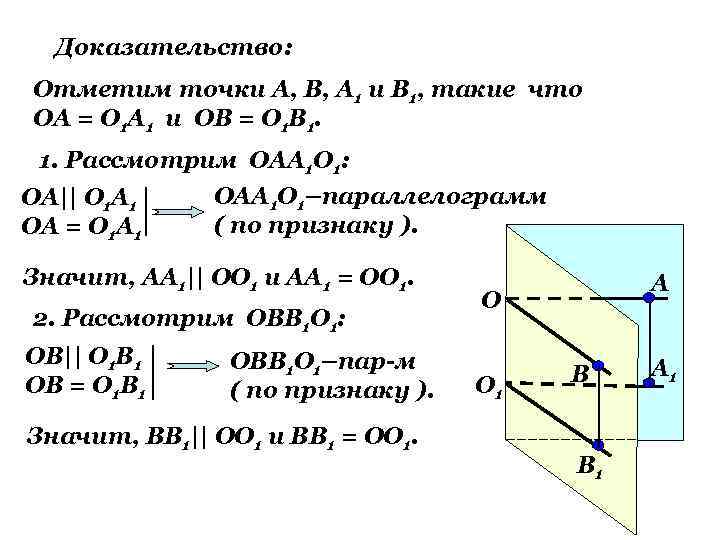Доказательство: Отметим точки А, В, А 1 и В 1, такие что ОА = О 1 А 1 и ОВ = О 1 В 1. 1. Рассмотрим ОАА 1 О 1: ОА|| О 1 А 1 ОА = О 1 А 1 ОАА 1 О 1–параллелограмм ( по признаку ). Значит, АА 1|| ОО 1 и АА 1 = ОО 1. 2. Рассмотрим ОВВ 1 О 1: ОВ|| О 1 В 1 ОВ = О 1 В 1 ОВВ 1 О 1–пар-м ( по признаку ). Значит, ВВ 1|| ОО 1 и ВВ 1 = ОО 1. А О О 1 В В 1 А 1

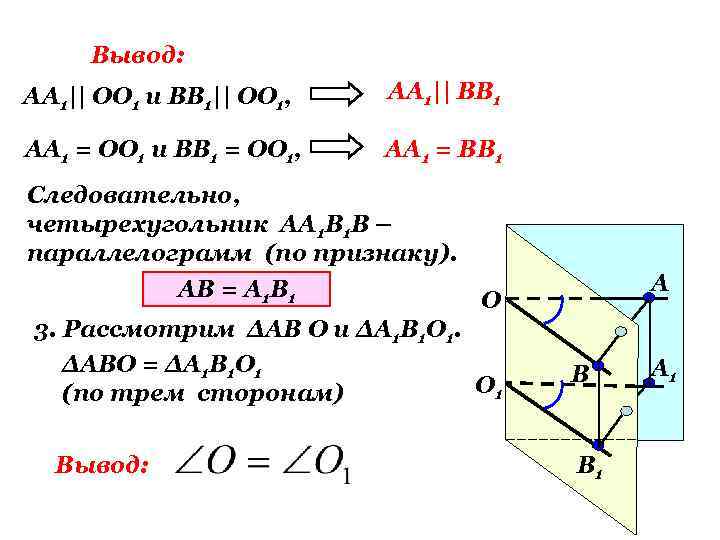Вывод: АА 1|| ОО 1 и ВВ 1|| ОО 1, АА 1|| ВВ 1 АА 1 = ОО 1 и ВВ 1 = ОО 1, АА 1 = ВВ 1 Следовательно, четырехугольник АА 1 В 1 В – параллелограмм (по признаку). АВ = А 1 В 1 О 3. Рассмотрим ∆АВ О и ∆А 1 В 1 О 1. ∆АВО = ∆А 1 В 1 О 1 (по трем сторонам) Вывод: А В В 1 А 1

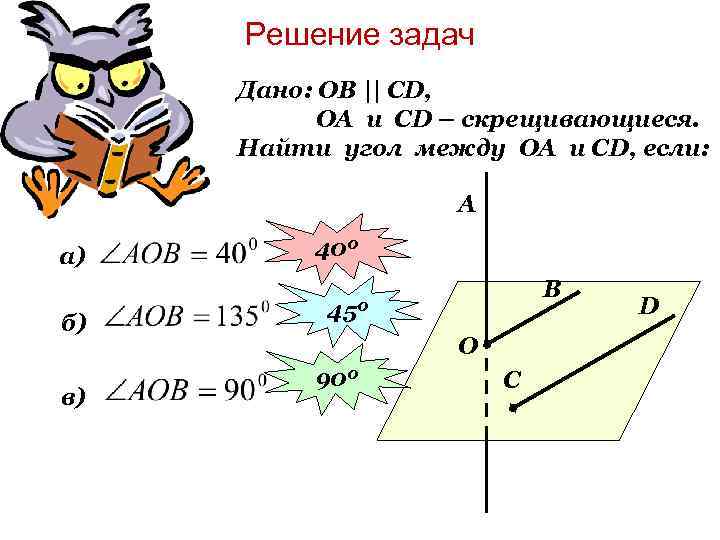Решение задач Дано: ОВ || СD, ОА и СD – скрещивающиеся. Найти угол между ОА и СD, если: A а) б) в) 400 В 450 О 900 C D

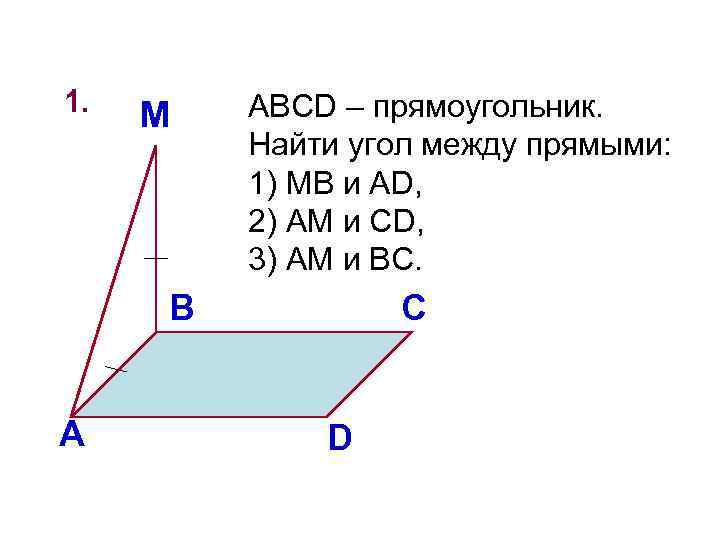1. M ABCD – прямоугольник. Найти угол между прямыми: 1) MB и AD, 2) AM и CD, 3) AM и BC. В А С D

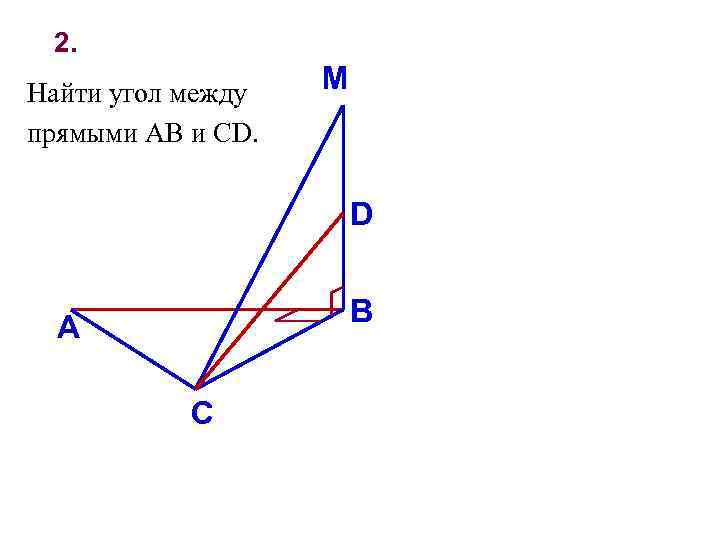2. Найти угол между прямыми AB и CD. M D В А С

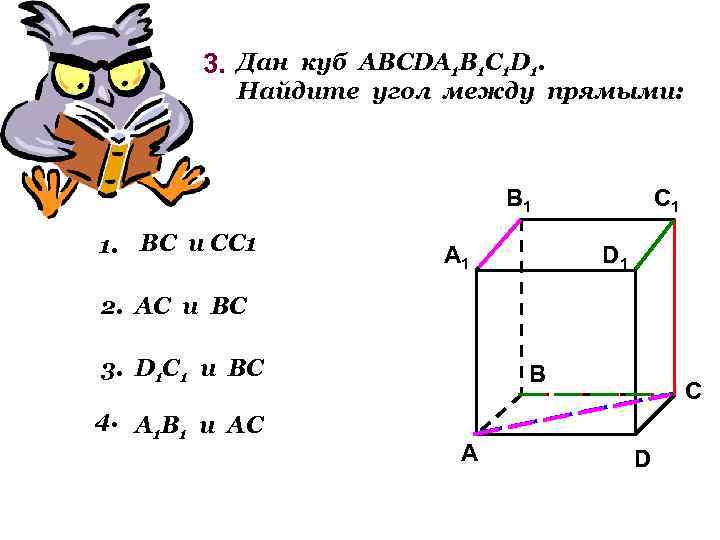3. Дан куб АВСDА 1 В 1 С 1 D 1. Найдите угол между прямыми: B 1 1. ВС и СС 1 A 1 C 1 D 1 2. АС и ВС 3. D 1 С 1 и ВС 4. А 1 В 1 и АС B A C D

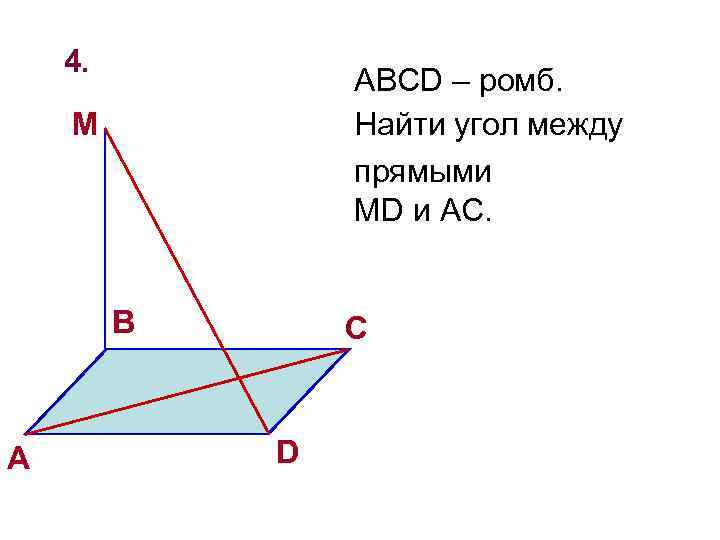4. ABCD – ромб. Найти угол между прямыми MD и AC. M B A C D

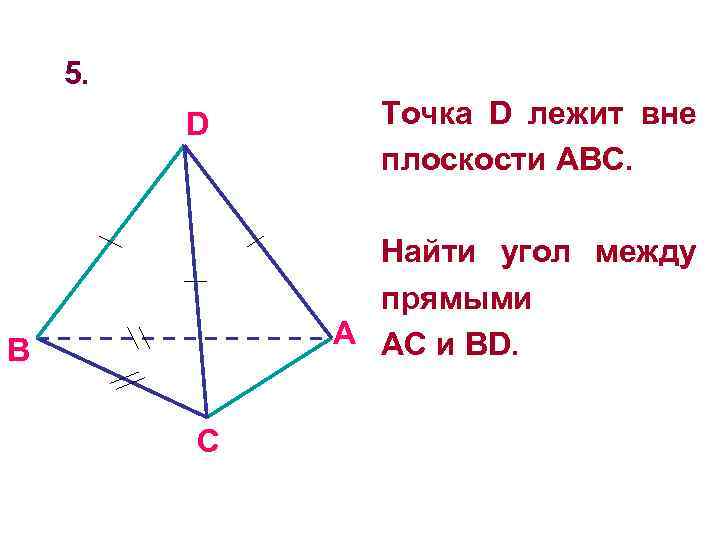5. D Точка D лежит вне плоскости АВС. Найти угол между прямыми A AC и BD. B C

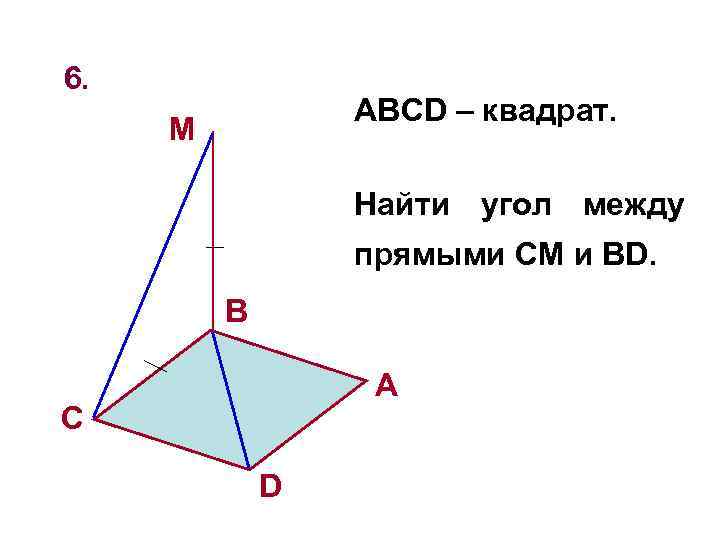6. ABCD – квадрат. M Найти угол между прямыми CM и BD. B A C D