Скорости сейсмических волн и плотность Vp


















Скорость-плотность.ppt
- Количество слайдов: 51
 Скорости сейсмических волн и плотность Vp = (( +2 )/ ) = (K+4 /3) Скорость продольных волн Vs = ( / ) Скорость поперечных волн Коэффициент Пуассона K/ =Vp 2 -(4/3)Vs 2
Скорости сейсмических волн и плотность Vp = (( +2 )/ ) = (K+4 /3) Скорость продольных волн Vs = ( / ) Скорость поперечных волн Коэффициент Пуассона K/ =Vp 2 -(4/3)Vs 2
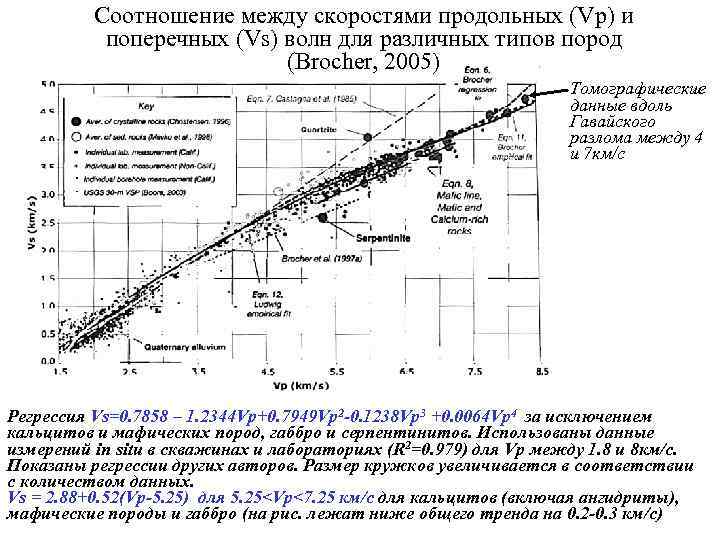
 Соотношение между скоростями продольных (Vp) и поперечных (Vs) волн для различных типов пород (Brocher, 2005) Томографические данные вдоль Гавайского разлома между 4 и 7 км/с Регрессия Vs=0. 7858 – 1. 2344 Vp+0. 7949 Vp 2 -0. 1238 Vp 3 +0. 0064 Vp 4 за исключением кальцитов и мафических пород, габбро и серпентинитов. Использованы данные измерений in situ в скважинах и лабораториях (R 2=0. 979) для Vp между 1. 8 и 8 км/с. Показаны регрессии других авторов. Размер кружков увеличивается в соответствии с количеством данных. Vs = 2. 88+0. 52(Vp-5. 25) для 5. 25
Соотношение между скоростями продольных (Vp) и поперечных (Vs) волн для различных типов пород (Brocher, 2005) Томографические данные вдоль Гавайского разлома между 4 и 7 км/с Регрессия Vs=0. 7858 – 1. 2344 Vp+0. 7949 Vp 2 -0. 1238 Vp 3 +0. 0064 Vp 4 за исключением кальцитов и мафических пород, габбро и серпентинитов. Использованы данные измерений in situ в скважинах и лабораториях (R 2=0. 979) для Vp между 1. 8 и 8 км/с. Показаны регрессии других авторов. Размер кружков увеличивается в соответствии с количеством данных. Vs = 2. 88+0. 52(Vp-5. 25) для 5. 25
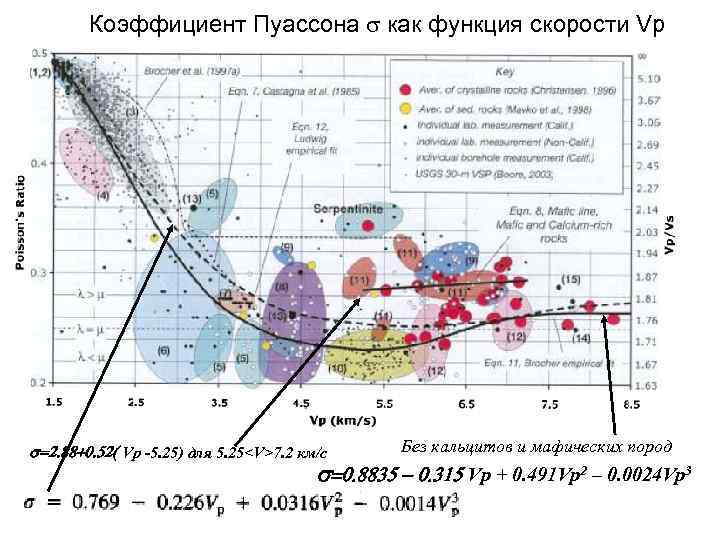
 Коэффициент Пуассона s как функция скорости Vp =2. 88+0. 52( Vp -5. 25) для 5. 25
Коэффициент Пуассона s как функция скорости Vp =2. 88+0. 52( Vp -5. 25) для 5. 25
 Идентификация групп пород для предыдущего рисунка.
Идентификация групп пород для предыдущего рисунка.
 Сравнение измеренной и рассчитанной по регрессиям скорости Vs для различных типов кристаллических пород Vp измерены, Vs – рассчитаны. Vs=0. 785 -1. 2344 Vp+0. 7949 Vp 2 -0. 1238 Vp 3+0. 0064 Vp 4 (6) Vs=0. 9409 + 2. 0947 Vp – 0. 8206 Vp 2+ 0. 2683 Vp 3 – 0. 0251 Vp 4 (12)
Сравнение измеренной и рассчитанной по регрессиям скорости Vs для различных типов кристаллических пород Vp измерены, Vs – рассчитаны. Vs=0. 785 -1. 2344 Vp+0. 7949 Vp 2 -0. 1238 Vp 3+0. 0064 Vp 4 (6) Vs=0. 9409 + 2. 0947 Vp – 0. 8206 Vp 2+ 0. 2683 Vp 3 – 0. 0251 Vp 4 (12)
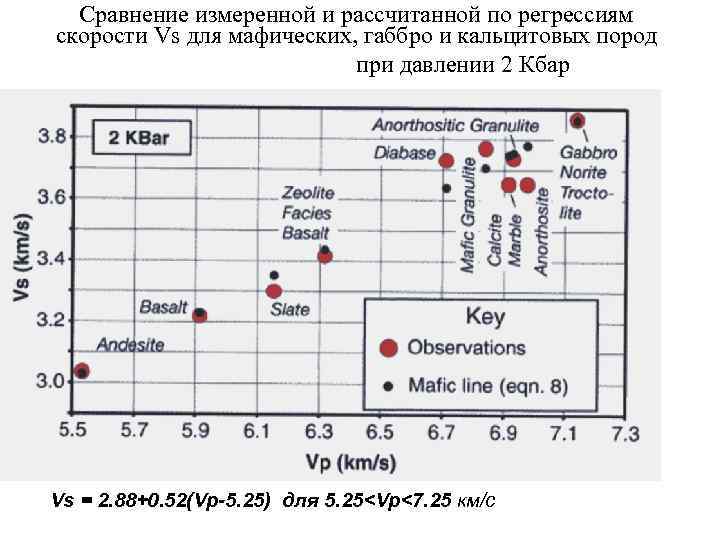
 Сравнение измеренной и рассчитанной по регрессиям скорости Vs для мафических, габбро и кальцитовых пород при давлении 2 Кбар Vs = 2. 88+0. 52(Vp-5. 25) для 5. 25
Сравнение измеренной и рассчитанной по регрессиям скорости Vs для мафических, габбро и кальцитовых пород при давлении 2 Кбар Vs = 2. 88+0. 52(Vp-5. 25) для 5. 25
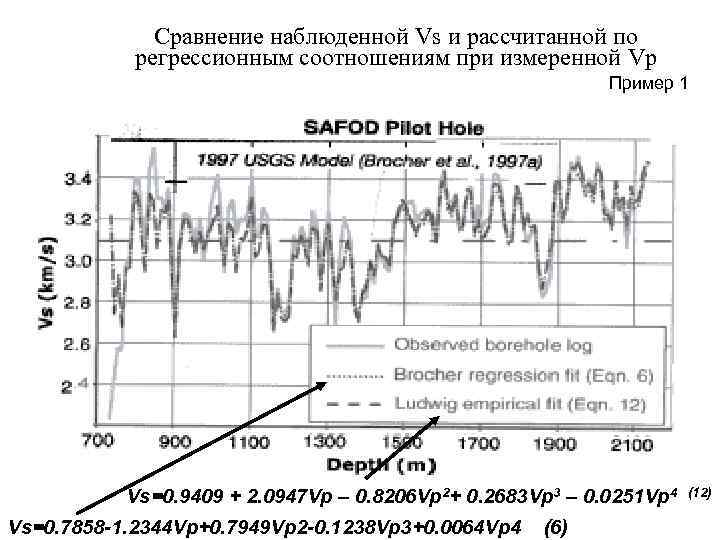
 Сравнение наблюденной Vs и рассчитанной по регрессионным соотношениям при измеренной Vp Пример 1 Vs=0. 9409 + 2. 0947 Vp – 0. 8206 Vp 2+ 0. 2683 Vp 3 – 0. 0251 Vp 4 (12) Vs=0. 7858 -1. 2344 Vp+0. 7949 Vp 2 -0. 1238 Vp 3+0. 0064 Vp 4 (6)
Сравнение наблюденной Vs и рассчитанной по регрессионным соотношениям при измеренной Vp Пример 1 Vs=0. 9409 + 2. 0947 Vp – 0. 8206 Vp 2+ 0. 2683 Vp 3 – 0. 0251 Vp 4 (12) Vs=0. 7858 -1. 2344 Vp+0. 7949 Vp 2 -0. 1238 Vp 3+0. 0064 Vp 4 (6)
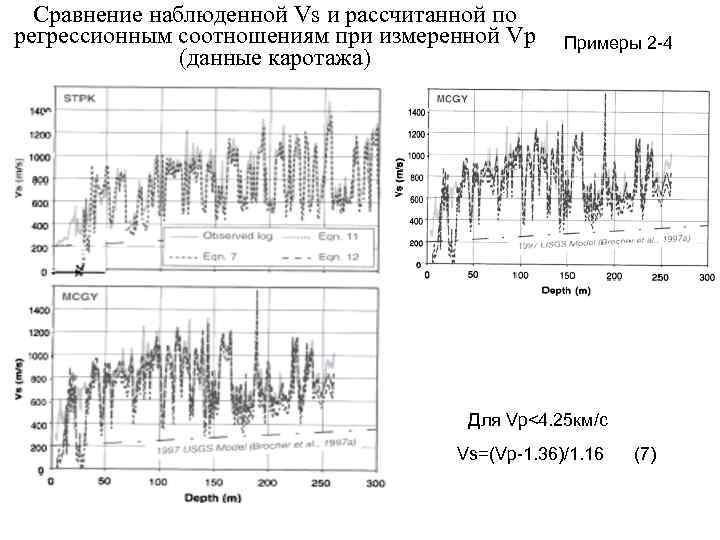
 Сравнение наблюденной Vs и рассчитанной по регрессионным соотношениям при измеренной Vp Примеры 2 -4 (данные каротажа) Для Vp<4. 25 км/с Vs=(Vp-1. 36)/1. 16 (7)
Сравнение наблюденной Vs и рассчитанной по регрессионным соотношениям при измеренной Vp Примеры 2 -4 (данные каротажа) Для Vp<4. 25 км/с Vs=(Vp-1. 36)/1. 16 (7)
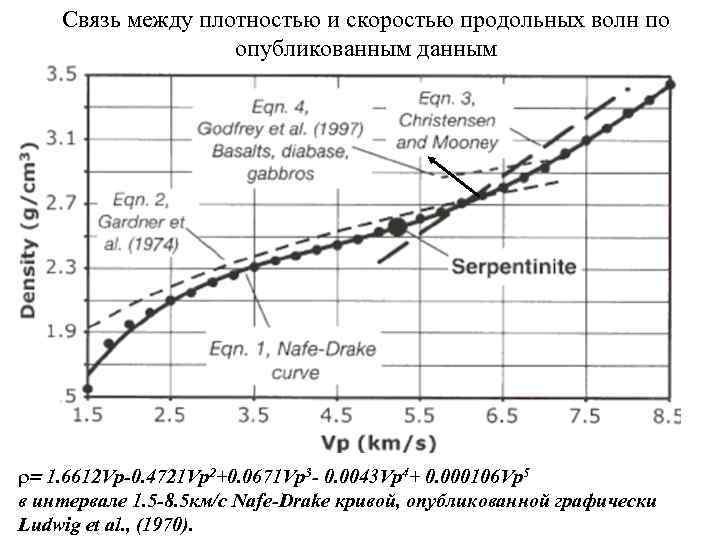
 Связь между плотностью и скоростью продольных волн по опубликованным данным = 1. 6612 Vp-0. 4721 Vp 2+0. 0671 Vp 3 - 0. 0043 Vp 4+ 0. 000106 Vp 5 в интервале 1. 5 -8. 5 км/с Nafe-Drake кривой, опубликованной графически Ludwig et al. , (1970).
Связь между плотностью и скоростью продольных волн по опубликованным данным = 1. 6612 Vp-0. 4721 Vp 2+0. 0671 Vp 3 - 0. 0043 Vp 4+ 0. 000106 Vp 5 в интервале 1. 5 -8. 5 км/с Nafe-Drake кривой, опубликованной графически Ludwig et al. , (1970).
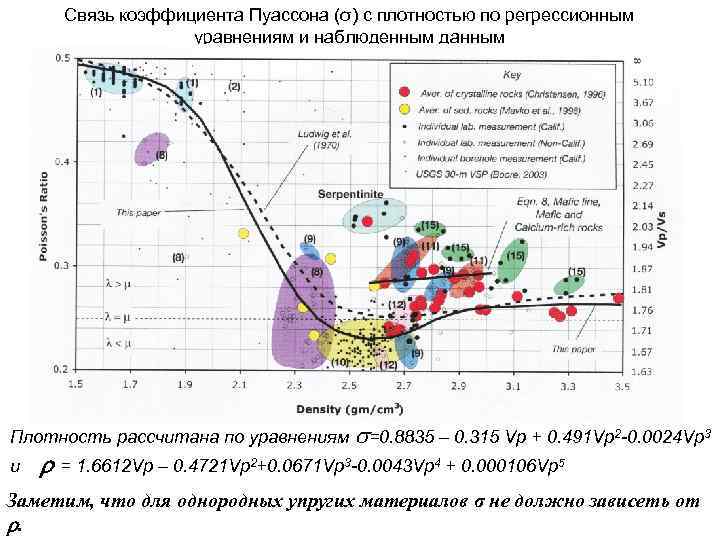
 Связь коэффициента Пуассона (σ) с плотностью по регрессионным уравнениям и наблюденным данным Плотность рассчитана по уравнениям =0. 8835 – 0. 315 Vp + 0. 491 Vp 2 -0. 0024 Vp 3 и = 1. 6612 Vp – 0. 4721 Vp 2+0. 0671 Vp 3 -0. 0043 Vp 4 + 0. 000106 Vp 5 Заметим, что для однородных упругих материалов σ не должно зависеть от .
Связь коэффициента Пуассона (σ) с плотностью по регрессионным уравнениям и наблюденным данным Плотность рассчитана по уравнениям =0. 8835 – 0. 315 Vp + 0. 491 Vp 2 -0. 0024 Vp 3 и = 1. 6612 Vp – 0. 4721 Vp 2+0. 0671 Vp 3 -0. 0043 Vp 4 + 0. 000106 Vp 5 Заметим, что для однородных упругих материалов σ не должно зависеть от .
 Идентификация групп пород для предыдущего рисунка.
Идентификация групп пород для предыдущего рисунка.
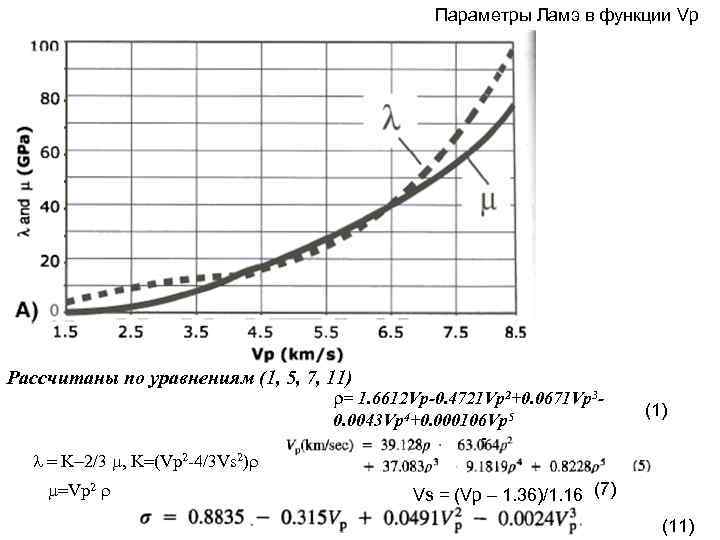
 Параметры Ламэ в функции Vp Рассчитаны по уравнениям (1, 5, 7, 11) = 1. 6612 Vp-0. 4721 Vp 2+0. 0671 Vp 3 - (1) 0. 0043 Vp 4+0. 000106 Vp 5 - = K-2/3 , K=(Vp 2 -4/3 Vs 2) - =Vp 2 Vs = (Vp – 1. 36)/1. 16 (7) (11)
Параметры Ламэ в функции Vp Рассчитаны по уравнениям (1, 5, 7, 11) = 1. 6612 Vp-0. 4721 Vp 2+0. 0671 Vp 3 - (1) 0. 0043 Vp 4+0. 000106 Vp 5 - = K-2/3 , K=(Vp 2 -4/3 Vs 2) - =Vp 2 Vs = (Vp – 1. 36)/1. 16 (7) (11)
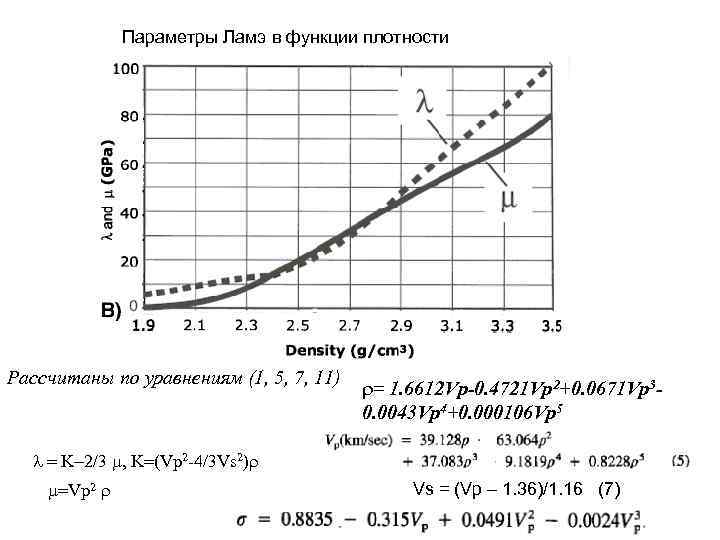
 Параметры Ламэ в функции плотности Рассчитаны по уравнениям (1, 5, 7, 11) = 1. 6612 Vp-0. 4721 Vp 2+0. 0671 Vp 3 - 0. 0043 Vp 4+0. 000106 Vp 5 = K-2/3 , K=(Vp 2 -4/3 Vs 2) =Vp 2 Vs = (Vp – 1. 36)/1. 16 (7)
Параметры Ламэ в функции плотности Рассчитаны по уравнениям (1, 5, 7, 11) = 1. 6612 Vp-0. 4721 Vp 2+0. 0671 Vp 3 - 0. 0043 Vp 4+0. 000106 Vp 5 = K-2/3 , K=(Vp 2 -4/3 Vs 2) =Vp 2 Vs = (Vp – 1. 36)/1. 16 (7)
 Способы определения вещественного состава по сейсмическим данным
Способы определения вещественного состава по сейсмическим данным
 Корреляционные зависимости между значениями скоростей Р- и S-волн, плотностью и содержаниями основных породообразующих окислов (по А. Л. Алейникову и др. 1991; С. Н. Кашубину, 1984) Основаны на измерениях по образцам горных пород Определяемые параметры: Корреляционное уравнение Коэффициент корреляции, Интервал изменения Плотность, г/см 3 ρ = 0. 18 Vp + 0. 40(Vp/Vs) + 1. 02 0. 93 2. 56 -3. 15 Содержание кремнезема, % ΣSi. O 2 = 152. 4 - 20. 82(Vp/Vs) - 2. 58(K/ρ) 0. 97 44 -76 Содержание окиси магния, % ΣMg. O = 0. 0109(K/ρ)2 + 0. 6588(K/ρ) + 18. 01(Vp/Vs)2 - 77. 5(Vp/Vs) + 55. 28 0. 94 1. 0 -11. 5 Содержание окиси кальция, % ΣCa. O = 1. 122(K/ρ) - 0. 89(Vp/Vs) - 17. 98 0. 94 0. 3 -14. 6 Суммарное содержание окислов железа, % ΣFe. O = 33. 225(Vp/Vs)2 - 106. 8(Vp/Vs) - 0. 0759(K/ρ)2 + 4. 343(K/ρ) + 33. 59 0. 88 2. 0 -15. 0 Примечания: Значения Vp и Vs в км/с; К/ρ = (Vp)2 - 4/3(Vs)2.
Корреляционные зависимости между значениями скоростей Р- и S-волн, плотностью и содержаниями основных породообразующих окислов (по А. Л. Алейникову и др. 1991; С. Н. Кашубину, 1984) Основаны на измерениях по образцам горных пород Определяемые параметры: Корреляционное уравнение Коэффициент корреляции, Интервал изменения Плотность, г/см 3 ρ = 0. 18 Vp + 0. 40(Vp/Vs) + 1. 02 0. 93 2. 56 -3. 15 Содержание кремнезема, % ΣSi. O 2 = 152. 4 - 20. 82(Vp/Vs) - 2. 58(K/ρ) 0. 97 44 -76 Содержание окиси магния, % ΣMg. O = 0. 0109(K/ρ)2 + 0. 6588(K/ρ) + 18. 01(Vp/Vs)2 - 77. 5(Vp/Vs) + 55. 28 0. 94 1. 0 -11. 5 Содержание окиси кальция, % ΣCa. O = 1. 122(K/ρ) - 0. 89(Vp/Vs) - 17. 98 0. 94 0. 3 -14. 6 Суммарное содержание окислов железа, % ΣFe. O = 33. 225(Vp/Vs)2 - 106. 8(Vp/Vs) - 0. 0759(K/ρ)2 + 4. 343(K/ρ) + 33. 59 0. 88 2. 0 -15. 0 Примечания: Значения Vp и Vs в км/с; К/ρ = (Vp)2 - 4/3(Vs)2.
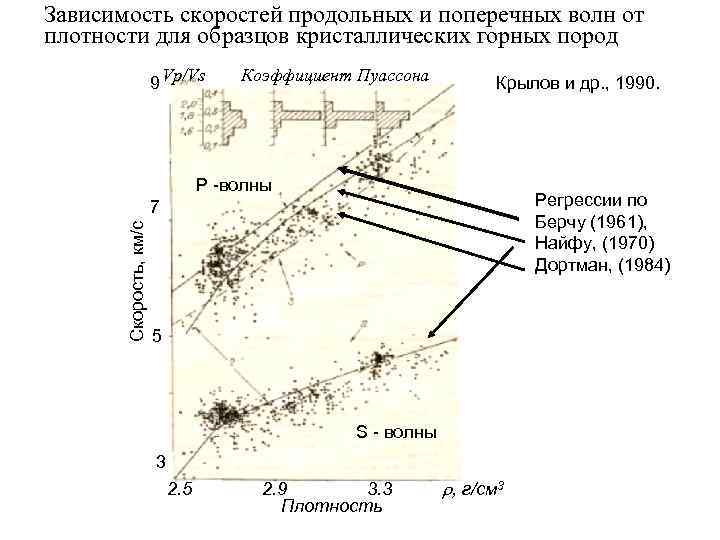
 Зависимость скоростей продольных и поперечных волн от плотности для образцов кристаллических горных пород 9 Vp/Vs Коэффициент Пуассона Крылов и др. , 1990. P -волны 7 Регрессии по Берчу (1961), Скорость, км/с Найфу, (1970) Дортман, (1984) 5 S - волны 3 2. 5 2. 9 3. 3 , г/см 3 Плотность
Зависимость скоростей продольных и поперечных волн от плотности для образцов кристаллических горных пород 9 Vp/Vs Коэффициент Пуассона Крылов и др. , 1990. P -волны 7 Регрессии по Берчу (1961), Скорость, км/с Найфу, (1970) Дортман, (1984) 5 S - волны 3 2. 5 2. 9 3. 3 , г/см 3 Плотность
 Зависимость плотности от скорости продольных (Vp) и поперечных (Vs) волн для кристаллических горных пород при давлении 1 Кбар (А) и 5 Кбар (Б). Vs A Изолинии: плотности коэффициента Пуассона Существенно, что в области 5. 5 -6. 5 км/с значения плотности не Б зависят от Vs. Vp
Зависимость плотности от скорости продольных (Vp) и поперечных (Vs) волн для кристаллических горных пород при давлении 1 Кбар (А) и 5 Кбар (Б). Vs A Изолинии: плотности коэффициента Пуассона Существенно, что в области 5. 5 -6. 5 км/с значения плотности не Б зависят от Vs. Vp
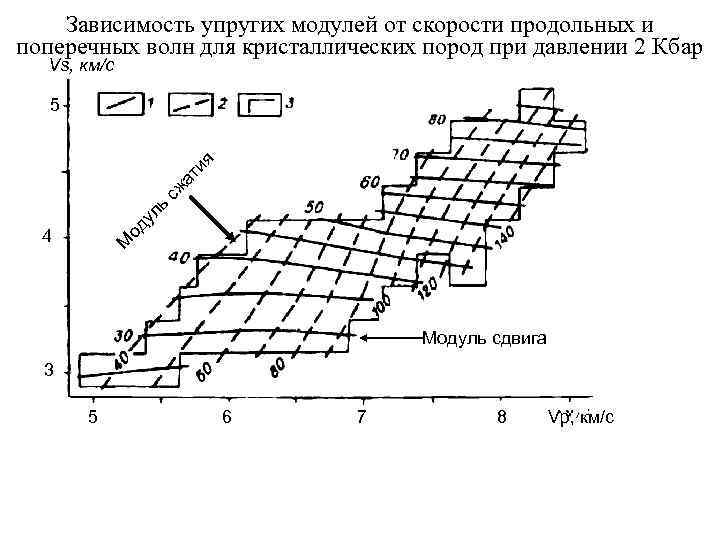
 Зависимость упругих модулей от скорости продольных и поперечных волн для кристаллических пород при давлении 2 Кбар Vs, км/с 5 ия ат сж ь ул од 4 М Модуль сдвига 3 5 6 7 8 Vp, км/с
Зависимость упругих модулей от скорости продольных и поперечных волн для кристаллических пород при давлении 2 Кбар Vs, км/с 5 ия ат сж ь ул од 4 М Модуль сдвига 3 5 6 7 8 Vp, км/с
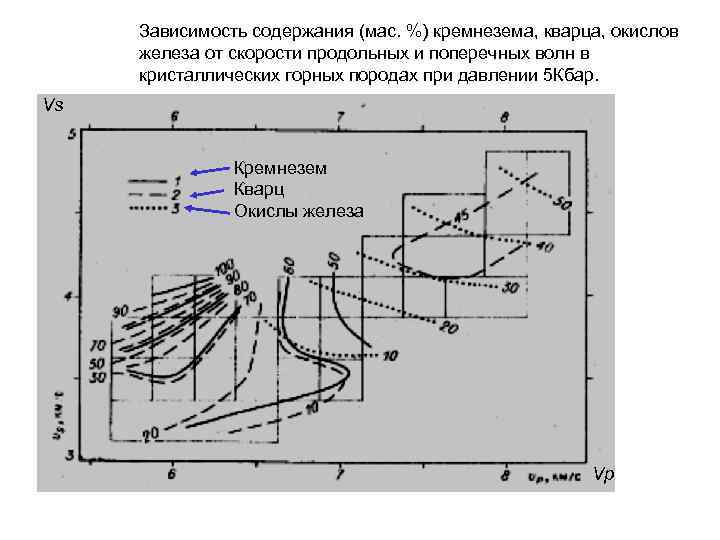
 Зависимость содержания (мас. %) кремнезема, кварца, окислов железа от скорости продольных и поперечных волн в кристаллических горных породах при давлении 5 Кбар. Vs Кремнезем Кварц Окислы железа Vp
Зависимость содержания (мас. %) кремнезема, кварца, окислов железа от скорости продольных и поперечных волн в кристаллических горных породах при давлении 5 Кбар. Vs Кремнезем Кварц Окислы железа Vp
 Обобщенные зависимости упругих параметров от глубины для БРЗ Vs Vp Коэффициент Плотность G K Пуассона
Обобщенные зависимости упругих параметров от глубины для БРЗ Vs Vp Коэффициент Плотность G K Пуассона
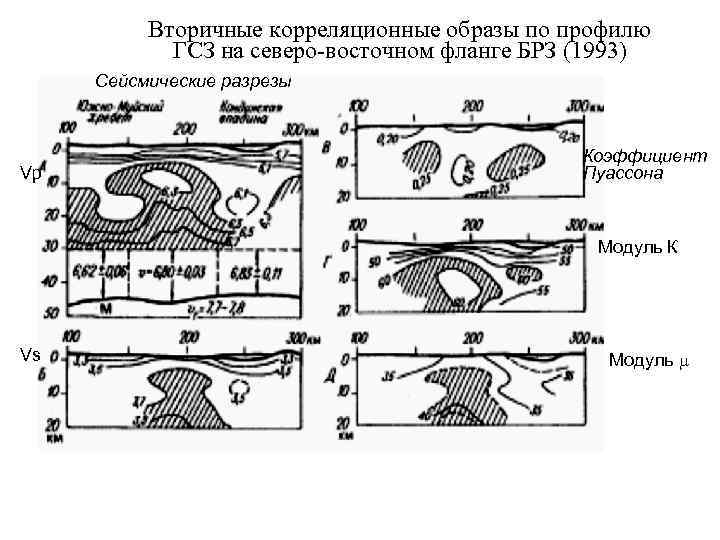
 Вторичные корреляционные образы по профилю ГСЗ на северо-восточном фланге БРЗ (1993) Сейсмические разрезы Коэффициент Vp Пуассона Модуль К Vs Модуль
Вторичные корреляционные образы по профилю ГСЗ на северо-восточном фланге БРЗ (1993) Сейсмические разрезы Коэффициент Vp Пуассона Модуль К Vs Модуль
 Коэффициент Пуассона и сейсмология кристаллических пород (Nikolas I. Christensen, 1996)
Коэффициент Пуассона и сейсмология кристаллических пород (Nikolas I. Christensen, 1996)
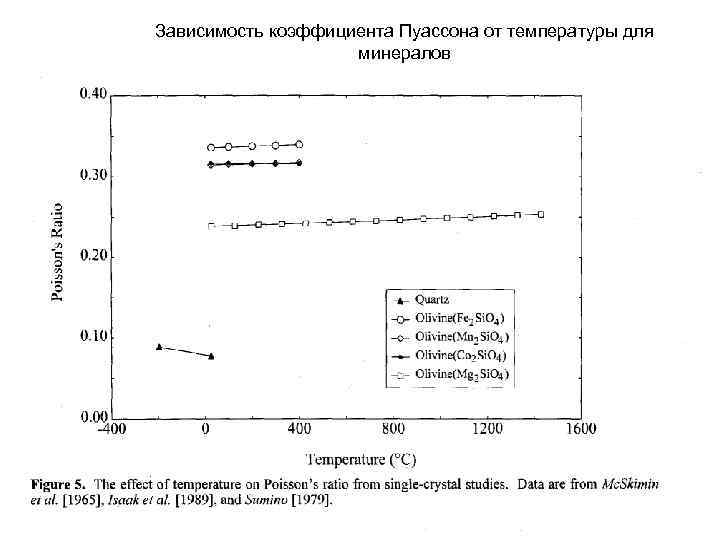
 Зависимость коэффициента Пуассона от температуры для минералов
Зависимость коэффициента Пуассона от температуры для минералов
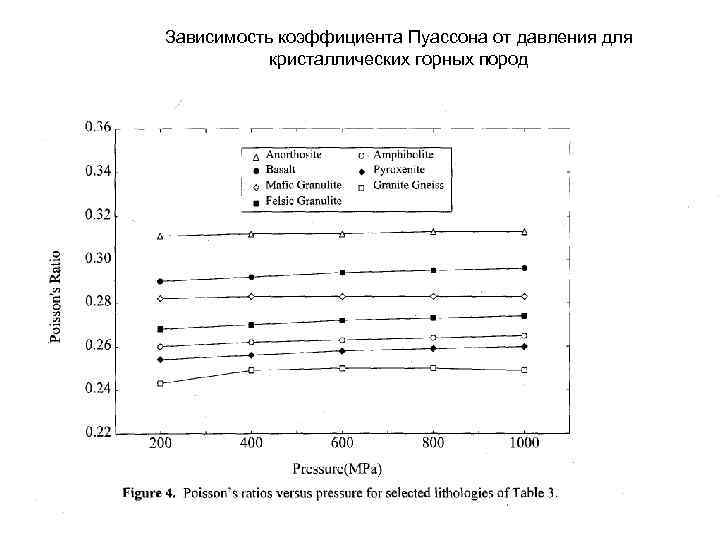
 Зависимость коэффициента Пуассона от давления для кристаллических горных пород
Зависимость коэффициента Пуассона от давления для кристаллических горных пород
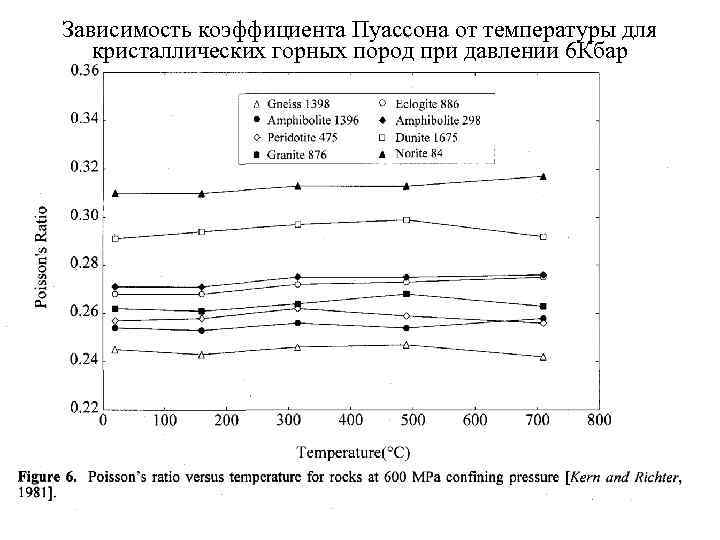
 Зависимость коэффициента Пуассона от температуры для кристаллических горных пород при давлении 6 Кбар
Зависимость коэффициента Пуассона от температуры для кристаллических горных пород при давлении 6 Кбар
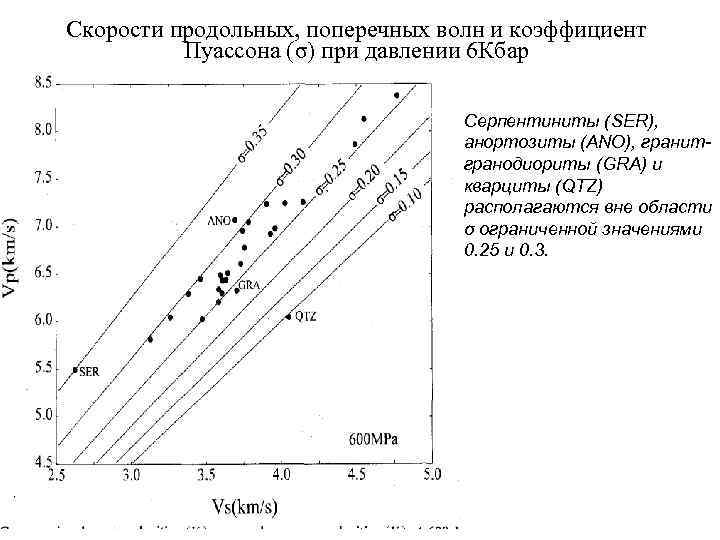
 Скорости продольных, поперечных волн и коэффициент Пуассона (σ) при давлении 6 Кбар Серпентиниты (SER), анортозиты (ANO), гранит- гранодиориты (GRA) и кварциты (QTZ) располагаются вне области σ ограниченной значениями 0. 25 и 0. 3.
Скорости продольных, поперечных волн и коэффициент Пуассона (σ) при давлении 6 Кбар Серпентиниты (SER), анортозиты (ANO), гранит- гранодиориты (GRA) и кварциты (QTZ) располагаются вне области σ ограниченной значениями 0. 25 и 0. 3.
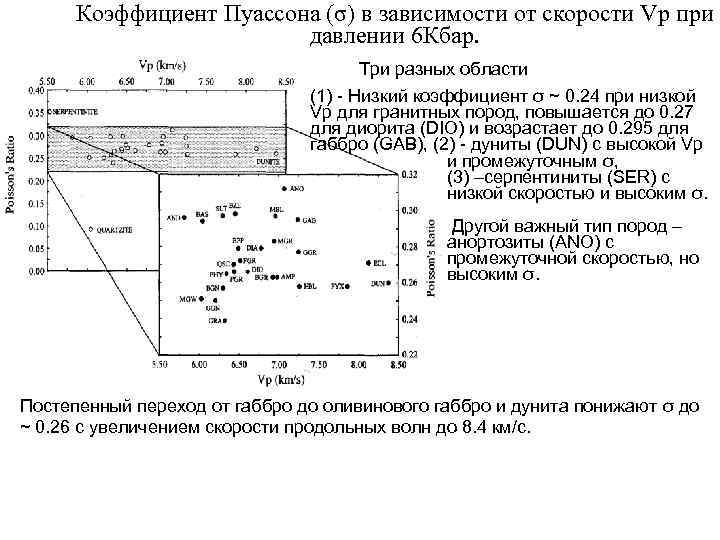
 Коэффициент Пуассона (σ) в зависимости от скорости Vp при давлении 6 Кбар. Три разных области (1) - Низкий коэффициент σ ~ 0. 24 при низкой Vp для гранитных пород, повышается до 0. 27 для диорита (DIO) и возрастает до 0. 295 для габбро (GAB), (2) - дуниты (DUN) с высокой Vp и промежуточным σ, (3) –серпентиниты (SER) с низкой скоростью и высоким σ. Другой важный тип пород – анортозиты (ANO) с промежуточной скоростью, но высоким σ. Постепенный переход от габбро до оливинового габбро и дунита понижают σ до ~ 0. 26 с увеличением скорости продольных волн до 8. 4 км/с.
Коэффициент Пуассона (σ) в зависимости от скорости Vp при давлении 6 Кбар. Три разных области (1) - Низкий коэффициент σ ~ 0. 24 при низкой Vp для гранитных пород, повышается до 0. 27 для диорита (DIO) и возрастает до 0. 295 для габбро (GAB), (2) - дуниты (DUN) с высокой Vp и промежуточным σ, (3) –серпентиниты (SER) с низкой скоростью и высоким σ. Другой важный тип пород – анортозиты (ANO) с промежуточной скоростью, но высоким σ. Постепенный переход от габбро до оливинового габбро и дунита понижают σ до ~ 0. 26 с увеличением скорости продольных волн до 8. 4 км/с.
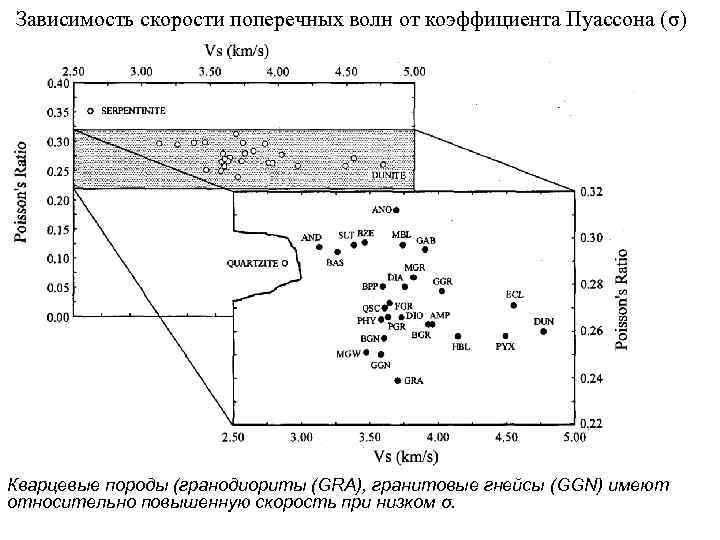
 Зависимость скорости поперечных волн от коэффициента Пуассона (σ) Кварцевые породы (гранодиориты (GRA), гранитовые гнейсы (GGN) имеют относительно повышенную скорость при низком σ.
Зависимость скорости поперечных волн от коэффициента Пуассона (σ) Кварцевые породы (гранодиориты (GRA), гранитовые гнейсы (GGN) имеют относительно повышенную скорость при низком σ.
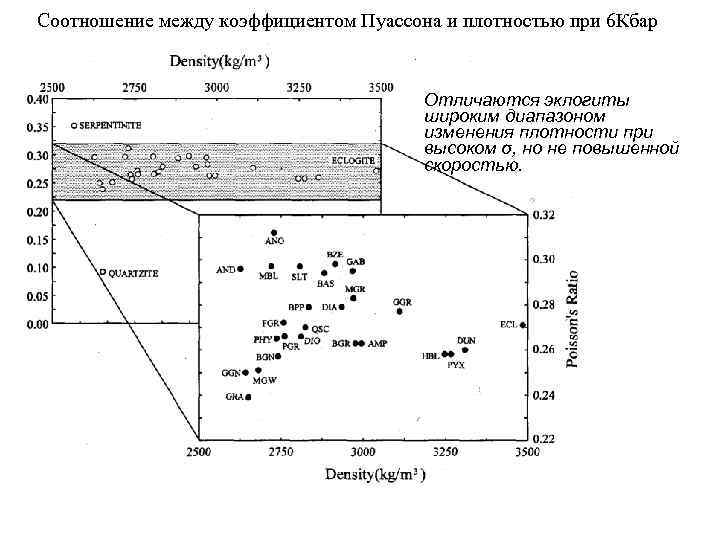
 Соотношение между коэффициентом Пуассона и плотностью при 6 Кбар Отличаются эклогиты широким диапазоном изменения плотности при высоком σ, но не повышенной скоростью.
Соотношение между коэффициентом Пуассона и плотностью при 6 Кбар Отличаются эклогиты широким диапазоном изменения плотности при высоком σ, но не повышенной скоростью.
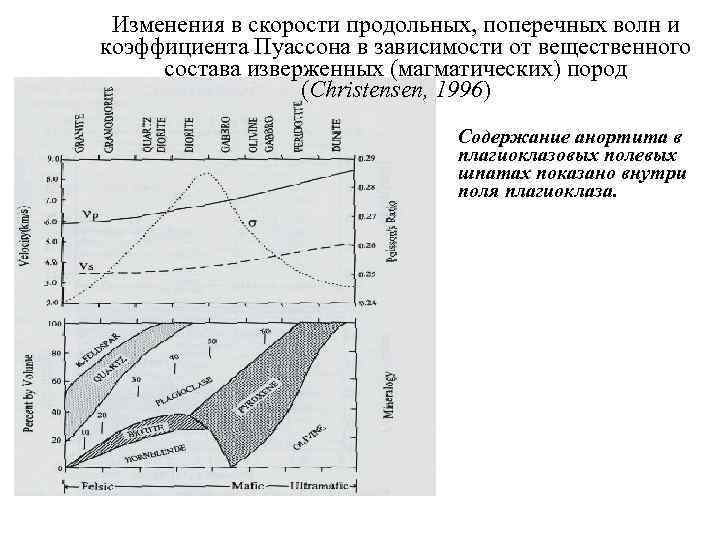
 Изменения в скорости продольных, поперечных волн и коэффициента Пуассона в зависимости от вещественного состава изверженных (магматических) пород (Christensen, 1996) Содержание анортита в плагиоклазовых полевых шпатах показано внутри поля плагиоклаза.
Изменения в скорости продольных, поперечных волн и коэффициента Пуассона в зависимости от вещественного состава изверженных (магматических) пород (Christensen, 1996) Содержание анортита в плагиоклазовых полевых шпатах показано внутри поля плагиоклаза.
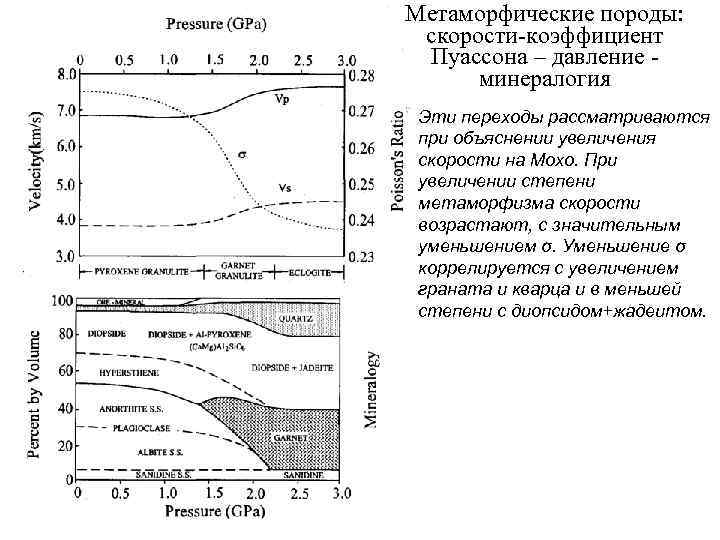
 Метаморфические породы: скорости-коэффициент Пуассона – давление - минералогия Эти переходы рассматриваются при объяснении увеличения скорости на Мохо. При увеличении степени метаморфизма скорости возрастают, с значительным уменьшением σ. Уменьшение σ коррелируется с увеличением граната и кварца и в меньшей степени с диопсидом+жадеитом.
Метаморфические породы: скорости-коэффициент Пуассона – давление - минералогия Эти переходы рассматриваются при объяснении увеличения скорости на Мохо. При увеличении степени метаморфизма скорости возрастают, с значительным уменьшением σ. Уменьшение σ коррелируется с увеличением граната и кварца и в меньшей степени с диопсидом+жадеитом.
 Выводы Зависимость плотности от скорости продольных и поперечных волн отличается многообразием для различных регионов. Общая регрессия для таких параметров, обеспечивающая достаточно высокую точность расчета плотности по сейсмическим данным, отсутствует. Задача решается отдельно для каждой из геологических структур. Необходимо использование сейсмических, петрологических данных и измерений на образцах горных пород при соответствующих условиях температуры и давления. Однако, при этом существует проблема учета масштаба. В естественных условиях геофизика имеет дело с большими объемами на много порядков превышающих образцы при лабораторных измерениях.
Выводы Зависимость плотности от скорости продольных и поперечных волн отличается многообразием для различных регионов. Общая регрессия для таких параметров, обеспечивающая достаточно высокую точность расчета плотности по сейсмическим данным, отсутствует. Задача решается отдельно для каждой из геологических структур. Необходимо использование сейсмических, петрологических данных и измерений на образцах горных пород при соответствующих условиях температуры и давления. Однако, при этом существует проблема учета масштаба. В естественных условиях геофизика имеет дело с большими объемами на много порядков превышающих образцы при лабораторных измерениях.
 Фактор порового давления на распределение скоростей продольных и поперечных волн и коэффициента Пуассона
Фактор порового давления на распределение скоростей продольных и поперечных волн и коэффициента Пуассона
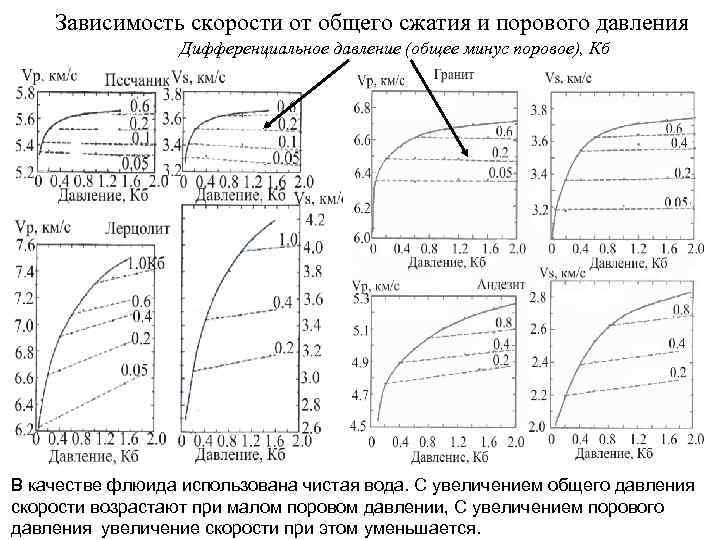
 Зависимость скорости от общего сжатия и порового давления Дифференциальное давление (общее минус поровое), Кб В качестве флюида использована чистая вода. С увеличением общего давления скорости возрастают при малом поровом давлении, С увеличением порового давления увеличение скорости при этом уменьшается.
Зависимость скорости от общего сжатия и порового давления Дифференциальное давление (общее минус поровое), Кб В качестве флюида использована чистая вода. С увеличением общего давления скорости возрастают при малом поровом давлении, С увеличением порового давления увеличение скорости при этом уменьшается.
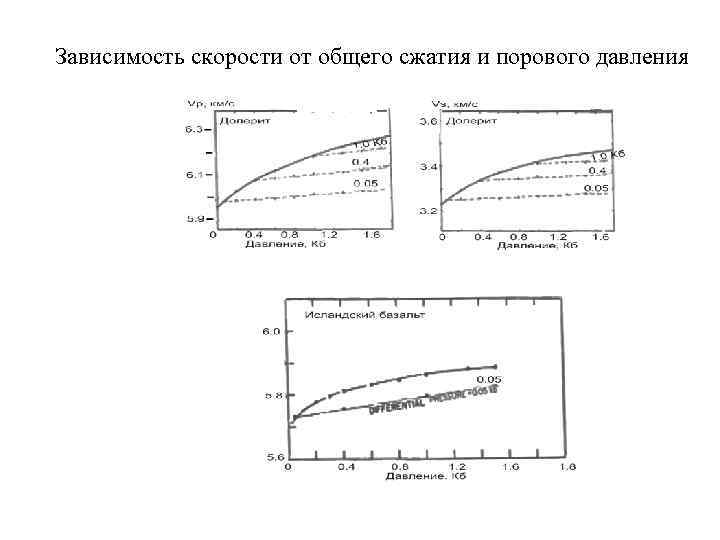
 Зависимость скорости от общего сжатия и порового давления
Зависимость скорости от общего сжатия и порового давления
 Различие влияния пористости на скорость продольных волн в осадочных и кристаллических породах Повышенное влияние пористости на скорость кристаллических пород обусловлено различным характером пористости. В кристаллических породах пористость трещинная (высокий коэффициент сжатия - вытянутости), в осадочных – поровая (низкое сжатие –поры изометричны). Уменьшение скорости продольных волн при 100 МПа общего давления обусловленного увеличенным поровым давлением 95 МПа.
Различие влияния пористости на скорость продольных волн в осадочных и кристаллических породах Повышенное влияние пористости на скорость кристаллических пород обусловлено различным характером пористости. В кристаллических породах пористость трещинная (высокий коэффициент сжатия - вытянутости), в осадочных – поровая (низкое сжатие –поры изометричны). Уменьшение скорости продольных волн при 100 МПа общего давления обусловленного увеличенным поровым давлением 95 МПа.
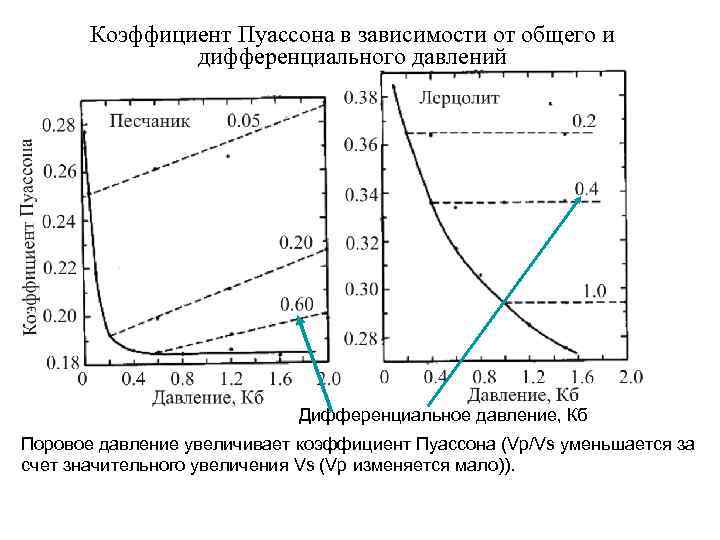
 Коэффициент Пуассона в зависимости от общего и дифференциального давлений Дифференциальное давление, Кб Поровое давление увеличивает коэффициент Пуассона (Vp/Vs уменьшается за счет значительного увеличения Vs (Vp изменяется мало)).
Коэффициент Пуассона в зависимости от общего и дифференциального давлений Дифференциальное давление, Кб Поровое давление увеличивает коэффициент Пуассона (Vp/Vs уменьшается за счет значительного увеличения Vs (Vp изменяется мало)).
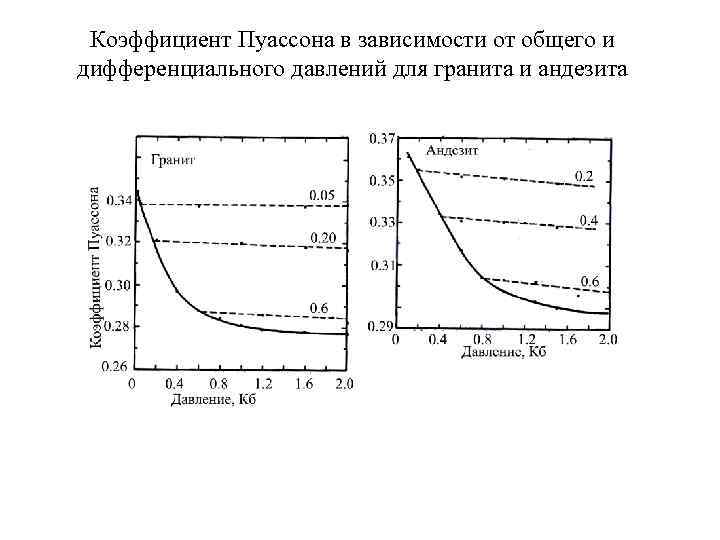
 Коэффициент Пуассона в зависимости от общего и дифференциального давлений для гранита и андезита
Коэффициент Пуассона в зависимости от общего и дифференциального давлений для гранита и андезита
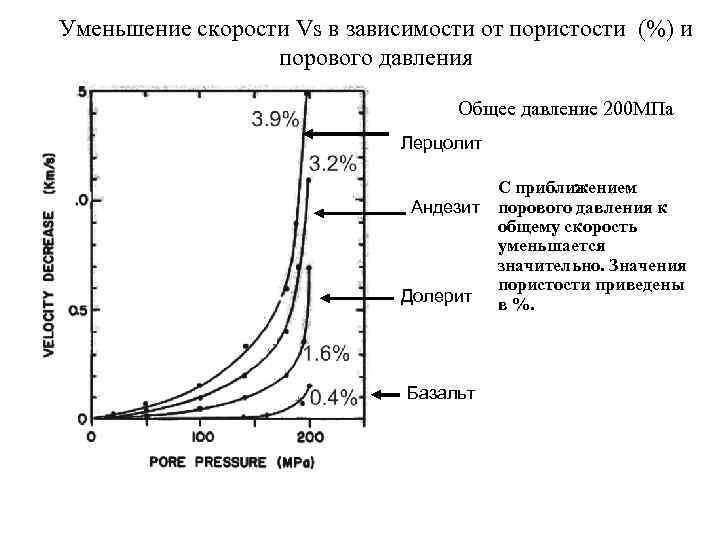
 Уменьшение скорости Vs в зависимости от пористости (%) и порового давления Общее давление 200 МПа Лерцолит С приближением Андезит порового давления к общему скорость уменьшается значительно. Значения пористости приведены Долерит в %. Базальт
Уменьшение скорости Vs в зависимости от пористости (%) и порового давления Общее давление 200 МПа Лерцолит С приближением Андезит порового давления к общему скорость уменьшается значительно. Значения пористости приведены Долерит в %. Базальт
 Концептуальная модель континентальной коры: Для континентальной коры вероятно, что многие из скоростных структур образованы давлением. Если водонасыщенные поры до глубины несколько км связаны с поверхностью, понижение скорости можно объяснить гидростатическим давлением. На большей глубине, где поры не связаны с поверхностью, давление определяется метаморфическими процессами, приводящими к увеличению порового давления и значительному уменьшению скоростей. Этим можно объяснить присутствие в коре волноводов на глубине 10 -20 км. Среднекоровые границы, как например, Конрада (где наблюдается) увеличение скоростей разделяют более напряженную верхнюю часть изверженных и метаморфических пород от нижних сухих. Скорости будут резко возрастать и электрическое сопротивление уменьшаться.
Концептуальная модель континентальной коры: Для континентальной коры вероятно, что многие из скоростных структур образованы давлением. Если водонасыщенные поры до глубины несколько км связаны с поверхностью, понижение скорости можно объяснить гидростатическим давлением. На большей глубине, где поры не связаны с поверхностью, давление определяется метаморфическими процессами, приводящими к увеличению порового давления и значительному уменьшению скоростей. Этим можно объяснить присутствие в коре волноводов на глубине 10 -20 км. Среднекоровые границы, как например, Конрада (где наблюдается) увеличение скоростей разделяют более напряженную верхнюю часть изверженных и метаморфических пород от нижних сухих. Скорости будут резко возрастать и электрическое сопротивление уменьшаться.
 Несколько главных вопросы возникают относительно порового флюида в в континентальной коре. Каковы вертикальные и латеральные распределения флюидов? До какой глубины поровые флюиды не остаются связанными через системы трещин с поверхностью? Какие геологические процессы являются ответственными за сохранение поровых флюидов на глубине? Являются ли водные флюиды или CO 2 более важными в качестве поровых флюидов в нижней части континентальный коры? Ответы на эти вопросы имеют важные значения для сейсмических свойств коры, так же как и другие физические свойства. Это тесно связано и с электрическими свойствами.
Несколько главных вопросы возникают относительно порового флюида в в континентальной коре. Каковы вертикальные и латеральные распределения флюидов? До какой глубины поровые флюиды не остаются связанными через системы трещин с поверхностью? Какие геологические процессы являются ответственными за сохранение поровых флюидов на глубине? Являются ли водные флюиды или CO 2 более важными в качестве поровых флюидов в нижней части континентальный коры? Ответы на эти вопросы имеют важные значения для сейсмических свойств коры, так же как и другие физические свойства. Это тесно связано и с электрическими свойствами.
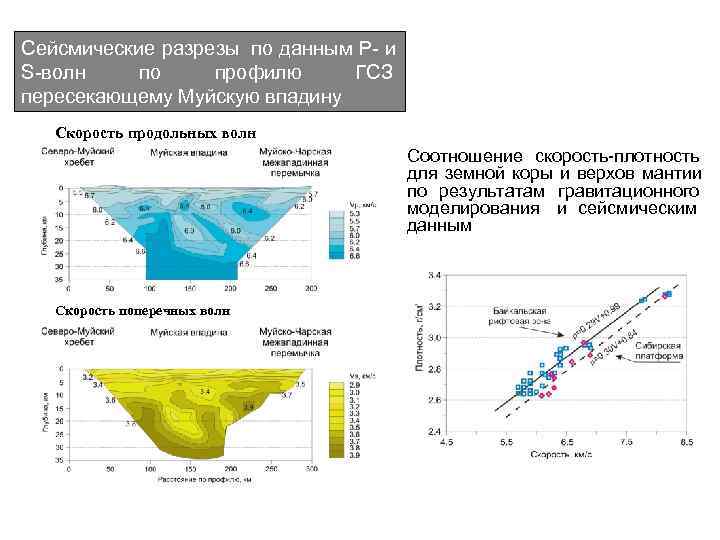
 Сейсмические разрезы по данным Р- и S-волн по профилю ГСЗ пересекающему Муйскую впадину Cкорость продольных волн Соотношение скорость-плотность для земной коры и верхов мантии по результатам гравитационного моделирования и сейсмическим данным Скорость поперечных волн
Сейсмические разрезы по данным Р- и S-волн по профилю ГСЗ пересекающему Муйскую впадину Cкорость продольных волн Соотношение скорость-плотность для земной коры и верхов мантии по результатам гравитационного моделирования и сейсмическим данным Скорость поперечных волн
 По совокупности экспериментальных данных ГСЗ, гравитационного моделирования и лабораторных измерений на образцах пород можно сделать попытку изучить состав и состояние вещества на глубине. Для этого предлагается использовать коэффициент петрофизической (химической) неоднородности (η) [ Буллен, 1955 ] , который определяется изменениями модуля сжатия и плотности с глубиной. Параметр петрофизической (химической) неоднородности К. Булленом была предложена следующая зависимость: η = K/ p –(1/g) Ф/ z, где Ф=К/ρ=Vp 2 -(4/3)Vs 2 К - модуль сжатия, р – литостатическое давление, g – ускорение силы тяжести, ρ – плотность, z – глубина, Vp, Vs – скорости продольных и поперечных волн. Теоретически величина η равна единице для однородных областей и отличается от единицы при отклонениях от однородности и при фазовых переходах.
По совокупности экспериментальных данных ГСЗ, гравитационного моделирования и лабораторных измерений на образцах пород можно сделать попытку изучить состав и состояние вещества на глубине. Для этого предлагается использовать коэффициент петрофизической (химической) неоднородности (η) [ Буллен, 1955 ] , который определяется изменениями модуля сжатия и плотности с глубиной. Параметр петрофизической (химической) неоднородности К. Булленом была предложена следующая зависимость: η = K/ p –(1/g) Ф/ z, где Ф=К/ρ=Vp 2 -(4/3)Vs 2 К - модуль сжатия, р – литостатическое давление, g – ускорение силы тяжести, ρ – плотность, z – глубина, Vp, Vs – скорости продольных и поперечных волн. Теоретически величина η равна единице для однородных областей и отличается от единицы при отклонениях от однородности и при фазовых переходах.
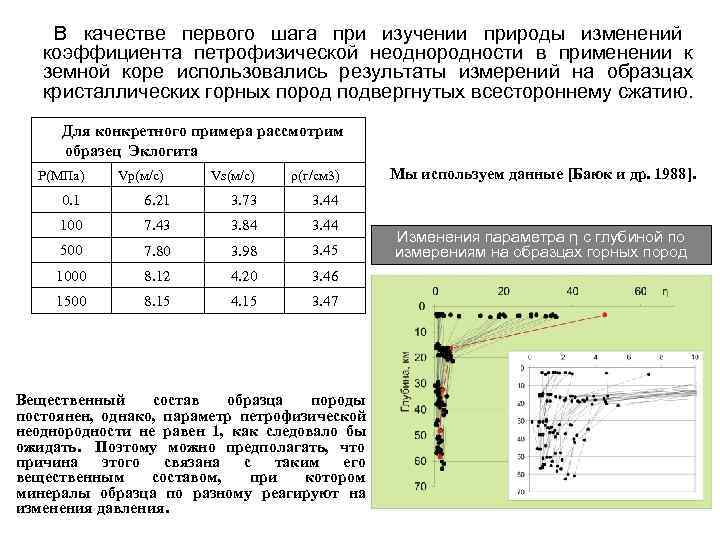
 В качестве первого шага при изучении природы изменений коэффициента петрофизической неоднородности в применении к земной коре использовались результаты измерений на образцах кристаллических горных пород подвергнутых всестороннему сжатию. Для конкретного примера рассмотрим образец Эклогита P(МПа) Vp(м/с) Vs(м/с) ρ(г/см 3) Мы используем данные [Баюк и др. 1988]. 0. 1 6. 21 3. 73 3. 44 100 7. 43 3. 84 3. 44 Изменения параметра η с глубиной по 500 7. 80 3. 98 3. 45 измерениям на образцах горных пород 1000 8. 12 4. 20 3. 46 1500 8. 15 4. 15 3. 47 Вещественный состав образца породы постоянен, однако, параметр петрофизической неоднородности не равен 1, как следовало бы ожидать. Поэтому можно предполагать, что причина этого связана с таким его вещественным составом, при котором минералы образца по разному реагируют на изменения давления.
В качестве первого шага при изучении природы изменений коэффициента петрофизической неоднородности в применении к земной коре использовались результаты измерений на образцах кристаллических горных пород подвергнутых всестороннему сжатию. Для конкретного примера рассмотрим образец Эклогита P(МПа) Vp(м/с) Vs(м/с) ρ(г/см 3) Мы используем данные [Баюк и др. 1988]. 0. 1 6. 21 3. 73 3. 44 100 7. 43 3. 84 3. 44 Изменения параметра η с глубиной по 500 7. 80 3. 98 3. 45 измерениям на образцах горных пород 1000 8. 12 4. 20 3. 46 1500 8. 15 4. 15 3. 47 Вещественный состав образца породы постоянен, однако, параметр петрофизической неоднородности не равен 1, как следовало бы ожидать. Поэтому можно предполагать, что причина этого связана с таким его вещественным составом, при котором минералы образца по разному реагируют на изменения давления.
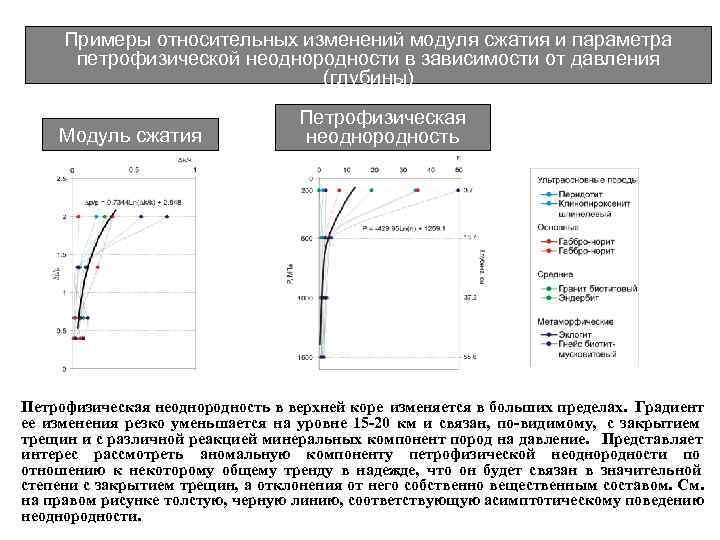
 Примеры относительных изменений модуля сжатия и параметра петрофизической неоднородности в зависимости от давления (глубины) Петрофизическая Модуль сжатия неоднородность Петрофизическая неоднородность в верхней коре изменяется в больших пределах. Градиент ее изменения резко уменьшается на уровне 15 -20 км и связан, по-видимому, с закрытием трещин и с различной реакцией минеральных компонент пород на давление. Представляет интерес рассмотреть аномальную компоненту петрофизической неоднородности по отношению к некоторому общему тренду в надежде, что он будет связан в значительной степени с закрытием трещин, а отклонения от него собственно вещественным составом. См. на правом рисунке толстую, черную линию, соответствующую асимптотическому поведению неоднородности.
Примеры относительных изменений модуля сжатия и параметра петрофизической неоднородности в зависимости от давления (глубины) Петрофизическая Модуль сжатия неоднородность Петрофизическая неоднородность в верхней коре изменяется в больших пределах. Градиент ее изменения резко уменьшается на уровне 15 -20 км и связан, по-видимому, с закрытием трещин и с различной реакцией минеральных компонент пород на давление. Представляет интерес рассмотреть аномальную компоненту петрофизической неоднородности по отношению к некоторому общему тренду в надежде, что он будет связан в значительной степени с закрытием трещин, а отклонения от него собственно вещественным составом. См. на правом рисунке толстую, черную линию, соответствующую асимптотическому поведению неоднородности.
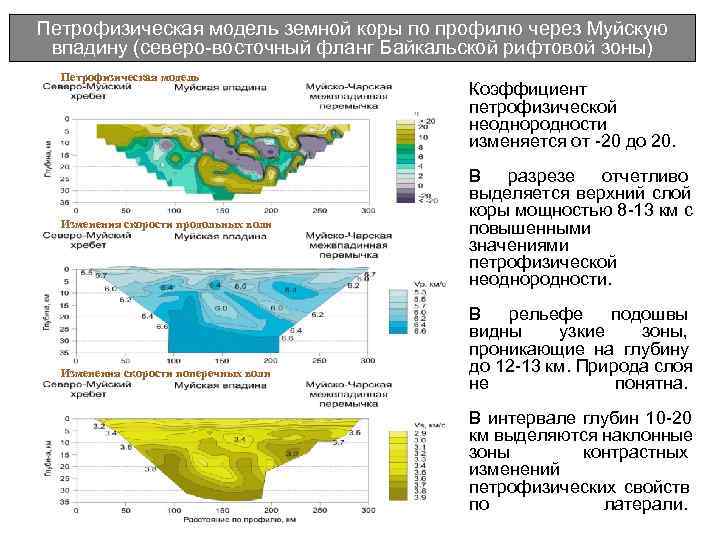
 Петрофизическая модель земной коры по профилю через Муйскую впадину (северо-восточный фланг Байкальской рифтовой зоны) Петрофизическая модель Коэффициент петрофизической неоднородности изменяется от -20 до 20. В разрезе отчетливо выделяется верхний слой коры мощностью 8 -13 км с Изменения скорости продольных волн повышенными значениями петрофизической неоднородности. В рельефе подошвы видны узкие зоны, проникающие на глубину Изменения скорости поперечных волн до 12 -13 км. Природа слоя не понятна. В интервале глубин 10 -20 км выделяются наклонные зоны контрастных изменений петрофизических свойств по латерали.
Петрофизическая модель земной коры по профилю через Муйскую впадину (северо-восточный фланг Байкальской рифтовой зоны) Петрофизическая модель Коэффициент петрофизической неоднородности изменяется от -20 до 20. В разрезе отчетливо выделяется верхний слой коры мощностью 8 -13 км с Изменения скорости продольных волн повышенными значениями петрофизической неоднородности. В рельефе подошвы видны узкие зоны, проникающие на глубину Изменения скорости поперечных волн до 12 -13 км. Природа слоя не понятна. В интервале глубин 10 -20 км выделяются наклонные зоны контрастных изменений петрофизических свойств по латерали.
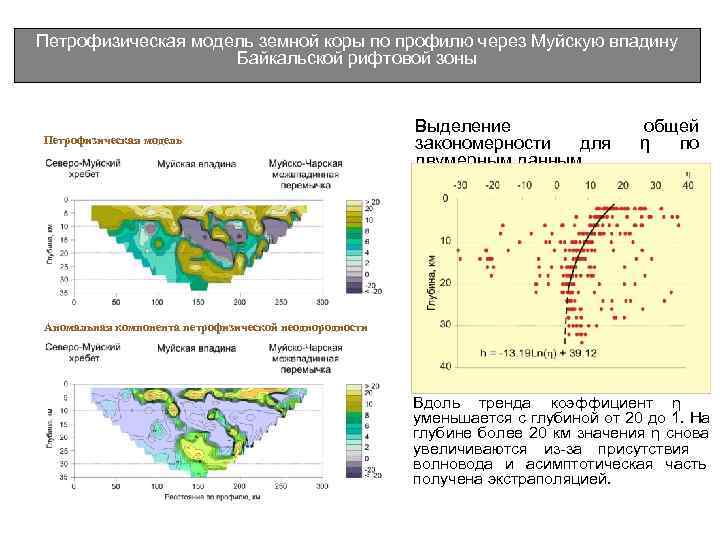
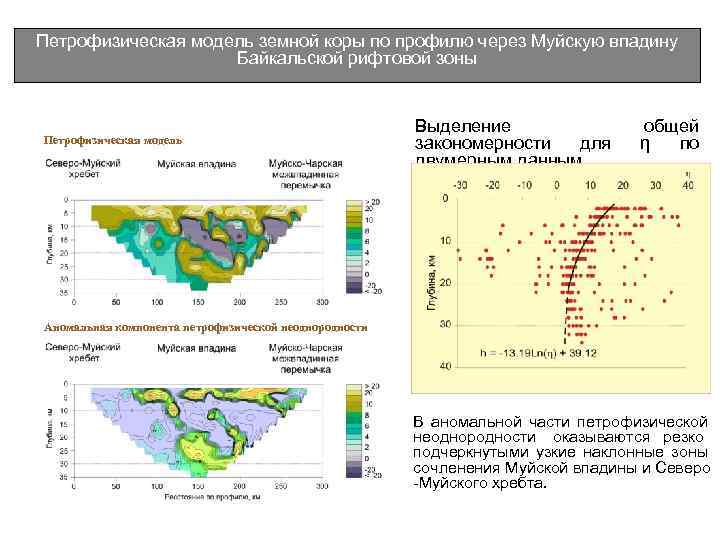
 Петрофизическая модель земной коры по профилю через Муйскую впадину Байкальской рифтовой зоны Выделение общей Петрофизическая модель закономерности для η по двумерным данным Аномальная компонента петрофизической неоднородности Вдоль тренда коэффициент η уменьшается с глубиной от 20 до 1. На глубине более 20 км значения η снова увеличиваются из-за присутствия волновода и асимптотическая часть получена экстраполяцией.
Петрофизическая модель земной коры по профилю через Муйскую впадину Байкальской рифтовой зоны Выделение общей Петрофизическая модель закономерности для η по двумерным данным Аномальная компонента петрофизической неоднородности Вдоль тренда коэффициент η уменьшается с глубиной от 20 до 1. На глубине более 20 км значения η снова увеличиваются из-за присутствия волновода и асимптотическая часть получена экстраполяцией.
 Петрофизическая модель земной коры по профилю через Муйскую впадину Байкальской рифтовой зоны Выделение общей Петрофизическая модель закономерности для η по двумерным данным Аномальная компонента петрофизической неоднородности В аномальной части петрофизической неоднородности оказываются резко подчеркнутыми узкие наклонные зоны сочленения Муйской впадины и Северо -Муйского хребта.
Петрофизическая модель земной коры по профилю через Муйскую впадину Байкальской рифтовой зоны Выделение общей Петрофизическая модель закономерности для η по двумерным данным Аномальная компонента петрофизической неоднородности В аномальной части петрофизической неоднородности оказываются резко подчеркнутыми узкие наклонные зоны сочленения Муйской впадины и Северо -Муйского хребта.
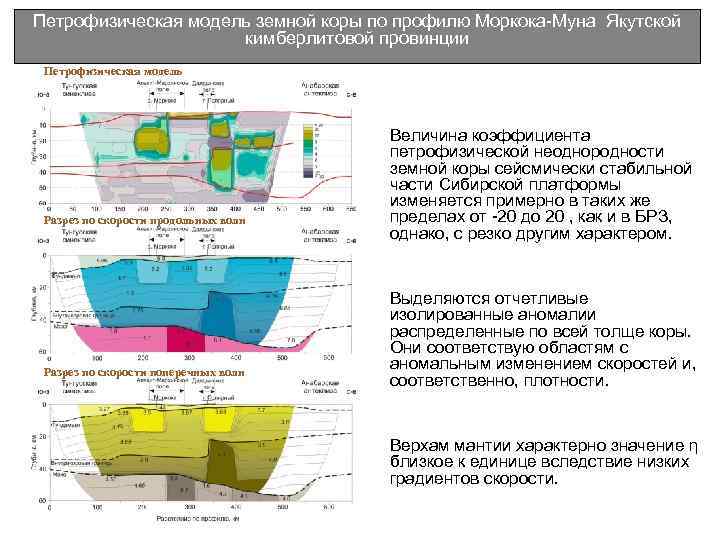
 Петрофизическая модель земной коры по профилю Моркока-Муна Якутской кимберлитовой провинции Петрофизическая модель Величина коэффициента петрофизической неоднородности земной коры сейсмически стабильной части Сибирской платформы изменяется примерно в таких же Разрез по скорости продольных волн пределах от -20 до 20 , как и в БРЗ, однако, с резко другим характером. Выделяются отчетливые изолированные аномалии распределенные по всей толще коры. Они соответствую областям с Разрез по скорости поперечных волн аномальным изменением скоростей и, соответственно, плотности. Верхам мантии характерно значение η близкое к единице вследствие низких градиентов скорости.
Петрофизическая модель земной коры по профилю Моркока-Муна Якутской кимберлитовой провинции Петрофизическая модель Величина коэффициента петрофизической неоднородности земной коры сейсмически стабильной части Сибирской платформы изменяется примерно в таких же Разрез по скорости продольных волн пределах от -20 до 20 , как и в БРЗ, однако, с резко другим характером. Выделяются отчетливые изолированные аномалии распределенные по всей толще коры. Они соответствую областям с Разрез по скорости поперечных волн аномальным изменением скоростей и, соответственно, плотности. Верхам мантии характерно значение η близкое к единице вследствие низких градиентов скорости.
 Петрофизическая модель земной коры по профилю Маркока-Муна Якутской кимберлитовой провинции Петрофизическая модель Выделение общей закономерности для η по двумерным данным Аномальная компонента петрофизической неоднородности
Петрофизическая модель земной коры по профилю Маркока-Муна Якутской кимберлитовой провинции Петрофизическая модель Выделение общей закономерности для η по двумерным данным Аномальная компонента петрофизической неоднородности
 Выводы 1. Значительные изменения коэффициента петрофизической неоднородности, измеренного на образцах горных пород предполагают его зависимость от трещиноватости и минеральной неоднородности, реагирующих на изменение давления. Существенно, что его величина уменьшается с ростом давления приближаясь к теоретическому значению для однородной среды близкому к единице. 2. Аналогичная закономерность выявляется и в земной коре по данным сейсмогравитационного моделирования. Так, в Байкальской рифтовой зоне эта неоднородность в целом уменьшается с глубиной от 20 -30 до 2 -3, стабилизируясь в интервале глубин 10 -20 км, где размещается наибольшее количество очагов землетрясений. В сейсмически стабильной Якутской кимберлитовой провинции тренд этой величины в земной коре оказывается практически постоянным около 2 -3. Вместе с тем, на фоне общего уменьшения наблюдаются значительные локальные аномалии. 3. Допуская, что общий тренд уменьшения коэффициента петрофизической неоднородности в земной коре с глубиной связан, главным образом, с закрытием трещин, можно выделить отклонения от него, которые могут быть связаны с изменениями вещественного состава. Характер распределения таких аномалий в земной коре сейсмически активной Байкальской рифтовой зоны и стабильной части Сибирской платформы имеют принципиально различный характер, подчеркивая различия в геодинамическом состоянии этих структур.
Выводы 1. Значительные изменения коэффициента петрофизической неоднородности, измеренного на образцах горных пород предполагают его зависимость от трещиноватости и минеральной неоднородности, реагирующих на изменение давления. Существенно, что его величина уменьшается с ростом давления приближаясь к теоретическому значению для однородной среды близкому к единице. 2. Аналогичная закономерность выявляется и в земной коре по данным сейсмогравитационного моделирования. Так, в Байкальской рифтовой зоне эта неоднородность в целом уменьшается с глубиной от 20 -30 до 2 -3, стабилизируясь в интервале глубин 10 -20 км, где размещается наибольшее количество очагов землетрясений. В сейсмически стабильной Якутской кимберлитовой провинции тренд этой величины в земной коре оказывается практически постоянным около 2 -3. Вместе с тем, на фоне общего уменьшения наблюдаются значительные локальные аномалии. 3. Допуская, что общий тренд уменьшения коэффициента петрофизической неоднородности в земной коре с глубиной связан, главным образом, с закрытием трещин, можно выделить отклонения от него, которые могут быть связаны с изменениями вещественного состава. Характер распределения таких аномалий в земной коре сейсмически активной Байкальской рифтовой зоны и стабильной части Сибирской платформы имеют принципиально различный характер, подчеркивая различия в геодинамическом состоянии этих структур.

