c7df58c54065b8d268f2bee5de30557c.ppt
- Количество слайдов: 23
 Školska godina 2006. /2007. Eksperimentalne metode moderne fizike Laseri Dr. sc. Nikola Godinovic (Nikola. Godinovic@fesb. hr)
Školska godina 2006. /2007. Eksperimentalne metode moderne fizike Laseri Dr. sc. Nikola Godinovic (Nikola. Godinovic@fesb. hr)
 Priča Vrlo brzo nakon što su izumljeni 1960. godine, laseri su postali novi izvori svjetlosti u znanstvenim laboratorijima širom svijeta. Danas se laseri koriste posvuda, u širokom spektru aplikacija poput prijenosa podataka, nadgledanja, zavarivanja, bar-code čitačima itd. Na slici je prikazana kirurška operacija pomoću laserskog svjetla prenesenog preko svjetlovoda. Svjetlost iz lasera, kao i iz bilo kojeg drugog izvora, nastaje emisijom atoma. Što je to onda tako drugačije kod laserske svjetlosti? Vjerovali ili ne, odgovor ćete saznati na današnjem predavanju http: //www. aip. org/success/industry/ 2
Priča Vrlo brzo nakon što su izumljeni 1960. godine, laseri su postali novi izvori svjetlosti u znanstvenim laboratorijima širom svijeta. Danas se laseri koriste posvuda, u širokom spektru aplikacija poput prijenosa podataka, nadgledanja, zavarivanja, bar-code čitačima itd. Na slici je prikazana kirurška operacija pomoću laserskog svjetla prenesenog preko svjetlovoda. Svjetlost iz lasera, kao i iz bilo kojeg drugog izvora, nastaje emisijom atoma. Što je to onda tako drugačije kod laserske svjetlosti? Vjerovali ili ne, odgovor ćete saznati na današnjem predavanju http: //www. aip. org/success/industry/ 2
 Interakcije fotona s atomom 3
Interakcije fotona s atomom 3
 Statistička fizika – pregled (1) q Statistička mehanika definira koji je najvjerojatniji način raspodijele dane količine energije između N čestica nekog sistema u termičkoj ravnoteži na temperaturi T. q Možemo procijeniti koliki je koliko čestica ima energiju E 1, koliko energiju E 2, itd. q Broj čestica N na energiji E: N(E)=g(E)f(E) n n g(E) – broj stanja na energiji E, statistička težina stanaj energije E. f(E) – funkcija raspodijele, srednji broj čestica u satnju s energijom E, vjerojatnost zaposjednuća stanja energije E 4
Statistička fizika – pregled (1) q Statistička mehanika definira koji je najvjerojatniji način raspodijele dane količine energije između N čestica nekog sistema u termičkoj ravnoteži na temperaturi T. q Možemo procijeniti koliki je koliko čestica ima energiju E 1, koliko energiju E 2, itd. q Broj čestica N na energiji E: N(E)=g(E)f(E) n n g(E) – broj stanja na energiji E, statistička težina stanaj energije E. f(E) – funkcija raspodijele, srednji broj čestica u satnju s energijom E, vjerojatnost zaposjednuća stanja energije E 4
 Statistička fizika – pregled (2) q 1. 2. 3. Statističko razmatranje razlikuje tri vrste čestice od kojih se neki sistem može sastojati. Identične čestice koje su dovoljno daleko da se mogu razlikovati, kao molekule u plinu. (Kavntno mehanički valne funkcije čestica se ne preklapaju). Maxwell-Boltzmanova funkcija (f. MB)raspodjele vrijedi za ovakav sistem Identične čestice cjelobrojnog spina (0, 1) koje ne možemo razlikovati jer im se valne funkcije preklapaju. Takve čestice nazivamo bozonima, a funkcija raspodjele koja s koristi za statističko razmatranje ovakvog sistema čestica je Bose. Einsteinova funkcija raspodijele (f. BE). Identične čestice, polu cjelobrojnog spina (1/2, 3/2, . . . ) koje ne možemo razlikovati, a zovemo ih fermioni. Fermioni ne mogu biti u istom kvantno mehaničkom stanju (Paulijev princip isključenja). Elektroni su fermioni. Fermi-Diracova (f. FD)funkcija raspodjele koristi se za statističko razmatranje fermiona. 5
Statistička fizika – pregled (2) q 1. 2. 3. Statističko razmatranje razlikuje tri vrste čestice od kojih se neki sistem može sastojati. Identične čestice koje su dovoljno daleko da se mogu razlikovati, kao molekule u plinu. (Kavntno mehanički valne funkcije čestica se ne preklapaju). Maxwell-Boltzmanova funkcija (f. MB)raspodjele vrijedi za ovakav sistem Identične čestice cjelobrojnog spina (0, 1) koje ne možemo razlikovati jer im se valne funkcije preklapaju. Takve čestice nazivamo bozonima, a funkcija raspodjele koja s koristi za statističko razmatranje ovakvog sistema čestica je Bose. Einsteinova funkcija raspodijele (f. BE). Identične čestice, polu cjelobrojnog spina (1/2, 3/2, . . . ) koje ne možemo razlikovati, a zovemo ih fermioni. Fermioni ne mogu biti u istom kvantno mehaničkom stanju (Paulijev princip isključenja). Elektroni su fermioni. Fermi-Diracova (f. FD)funkcija raspodjele koristi se za statističko razmatranje fermiona. 5
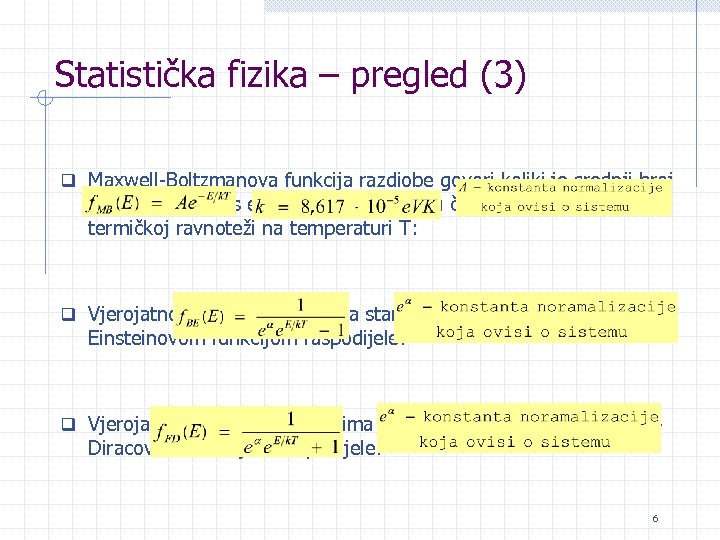 Statistička fizika – pregled (3) q Maxwell-Boltzmanova funkcija razdiobe govori koliki je srednji broj čestica u stanju s energijom E u sistemu čestica koji se nalazi termičkoj ravnoteži na temperaturi T: q Vjerojatnost da bozon zauzima stanje energije E je dana Bose- Einsteinovom funkcijom raspodijele: q Vjerojatnost da fermion zauzima stanje energije E je dana Fermi- Diracovom funkcijom raspodijele: 6
Statistička fizika – pregled (3) q Maxwell-Boltzmanova funkcija razdiobe govori koliki je srednji broj čestica u stanju s energijom E u sistemu čestica koji se nalazi termičkoj ravnoteži na temperaturi T: q Vjerojatnost da bozon zauzima stanje energije E je dana Bose- Einsteinovom funkcijom raspodijele: q Vjerojatnost da fermion zauzima stanje energije E je dana Fermi- Diracovom funkcijom raspodijele: 6
 Statistička fizika – pregled (4) q Prvo pobuđeno stanje E 2 atoma vodika je 10, 2 e. V iznad osnovnog stanja E 1. Koliki je omjer atoma u prvom pobuđenom stanju u odnosu na osnovno stanje na temperaturi (a) T= 300 K i (b) T=5800 K q Broj atoma u stanju energije je: q Omjer broja čestica u stanju s energijom E 1 i E 2 je: q Gustoća stanja osnovnog stanja g 1 je 2, a prvog pobuđenog stanja g 2 je 8. Konstanta A je ista jer se razmatra broj stanja unutar istog sistema. g 2/g 1=4. q Za T=300 K (k. T=0, 026 e. V), n 2/n 1=10 -171 q Za T=5800 K (k. T=0, 5 e. V), n 2/n 1=10 -8 q Na sobnim temperaturama (T=300 k) kontejner ispunjen vodikom ne emitira svijetlo. Na površini Sunca temperatura je 5800 K, te je u jednom molu vodika na Suncu ima 1015 atoma vodika u pobuđenom stanju (n 2=n 1 10 -8=1023 10 -8=1015 7
Statistička fizika – pregled (4) q Prvo pobuđeno stanje E 2 atoma vodika je 10, 2 e. V iznad osnovnog stanja E 1. Koliki je omjer atoma u prvom pobuđenom stanju u odnosu na osnovno stanje na temperaturi (a) T= 300 K i (b) T=5800 K q Broj atoma u stanju energije je: q Omjer broja čestica u stanju s energijom E 1 i E 2 je: q Gustoća stanja osnovnog stanja g 1 je 2, a prvog pobuđenog stanja g 2 je 8. Konstanta A je ista jer se razmatra broj stanja unutar istog sistema. g 2/g 1=4. q Za T=300 K (k. T=0, 026 e. V), n 2/n 1=10 -171 q Za T=5800 K (k. T=0, 5 e. V), n 2/n 1=10 -8 q Na sobnim temperaturama (T=300 k) kontejner ispunjen vodikom ne emitira svijetlo. Na površini Sunca temperatura je 5800 K, te je u jednom molu vodika na Suncu ima 1015 atoma vodika u pobuđenom stanju (n 2=n 1 10 -8=1023 10 -8=1015 7
 Stimulirana emisija q Razmotrimo nakupinu atoma na temperaturi T u vanjskom elektromagnetskom polju 8
Stimulirana emisija q Razmotrimo nakupinu atoma na temperaturi T u vanjskom elektromagnetskom polju 8
 Stimulirana emisija 9
Stimulirana emisija 9
 Laseri i laserska svjetlost (1) q U kasnim 1940. -tim i ranim 1960. -tim kvantna fizika je napravila dva ogromna doprinosa modernim tehnologijama: tranzistori i laseri. q Laserska svjetlost, kao i svjetlost npr. iz obične žarulje, je emitirana prijelazu atoma iz višeg u niže energijskog stanje. Međutim, za razliku od običnih izvora svjetlosti, u laserima atomi djeluju zajedno da bi proizveli svjetlost sa sljedećim karakteristikama: 1. Laserska svjetlost je visoko monokromatska, tj. sastavljena od samo jedne frekvencije. Svjetlost iz običnih (bijelih) žarulja je sastavljena od mnoštva različitih valnih duljine i stoga sigurno nije monokromatska. Čistoća laserske svjetlosti može biti do 1 dio u 1015. 2. Laserska svjetlost je vrlo koherentna, tj. fotoni su međusobno u fazi. Primjer: http: //www. colorado. edu/physics/2000/index. pl 10
Laseri i laserska svjetlost (1) q U kasnim 1940. -tim i ranim 1960. -tim kvantna fizika je napravila dva ogromna doprinosa modernim tehnologijama: tranzistori i laseri. q Laserska svjetlost, kao i svjetlost npr. iz obične žarulje, je emitirana prijelazu atoma iz višeg u niže energijskog stanje. Međutim, za razliku od običnih izvora svjetlosti, u laserima atomi djeluju zajedno da bi proizveli svjetlost sa sljedećim karakteristikama: 1. Laserska svjetlost je visoko monokromatska, tj. sastavljena od samo jedne frekvencije. Svjetlost iz običnih (bijelih) žarulja je sastavljena od mnoštva različitih valnih duljine i stoga sigurno nije monokromatska. Čistoća laserske svjetlosti može biti do 1 dio u 1015. 2. Laserska svjetlost je vrlo koherentna, tj. fotoni su međusobno u fazi. Primjer: http: //www. colorado. edu/physics/2000/index. pl 10
 Laseri i laserska svjetlost (2) 3. Laserska svjetlost je jako usmjerena. 4. Laserska svjetlost može se oštro fokusirati. Npr. laserski puls korišten za mjerenje udaljenosti mjeseca napravio je točku na mjesečevoj površini radijusa od samo nekoliko metara. Svjetlost iz obične žarulje može se usmjeriti pomoću leća, ali nikad tako dobro kao laserska svjetlost. Ako dva svjetlosna snopa imaju istu energiju, snop koji se fokusira u manju točku imat će veći intenzitet. Da bi dobili intenzitet svjetlosti koju daju jaki laseri tijelo bi trebalo zagrijati na temperaturu 1030 K (radi usporedbe, volframova nit u žarulji je ugrijana na 3000 K, a temperatura u jezgri sunca je 108 K). 11
Laseri i laserska svjetlost (2) 3. Laserska svjetlost je jako usmjerena. 4. Laserska svjetlost može se oštro fokusirati. Npr. laserski puls korišten za mjerenje udaljenosti mjeseca napravio je točku na mjesečevoj površini radijusa od samo nekoliko metara. Svjetlost iz obične žarulje može se usmjeriti pomoću leća, ali nikad tako dobro kao laserska svjetlost. Ako dva svjetlosna snopa imaju istu energiju, snop koji se fokusira u manju točku imat će veći intenzitet. Da bi dobili intenzitet svjetlosti koju daju jaki laseri tijelo bi trebalo zagrijati na temperaturu 1030 K (radi usporedbe, volframova nit u žarulji je ugrijana na 3000 K, a temperatura u jezgri sunca je 108 K). 11
 Kako rade laseri (1) q q q Riječ laser je kratica engleskog izraza “light amplification by the stimulated emission of radiation”, što se prevodi kao “pojačanje svjetlosti stimuliranom emisijom radijacije”. Ovaj koncept je uveo Einstein 1917. godine, dok je prvi laser napravljen 1960. Razmotrimo izolirani atom koji može biti ili u svom osnovnom stanju (stanju s najnižom energijom) E 0, ili u pobuđenom stanju (stanju s višom energijom) Ex. Postoje tri različita fizikalna procesa kroz koje atom može prelaziti iz jednog u drugo stanje. 1. Apsorpcija. Atom se u početku nalazi u osnovnom stanju. Ako ga stavimo u elektromagnetsko polje frekvencije , atom može apsorbirati energiju h iz tog polja i preći u više energijsko stanja. Iz zakona sačuvanja energije imamo h =Ex-E 0. 2. Spontana emisija. Atom se na početku nalazi u pobuđenom stanju i nema vanjskog zračenja. Nakon nekog vremene, atom će spontano (“sam od sebe”) preći u osnovno stanje, emitirajući foton energije h. Ovaj proces zovemo spontana emisija, jer se događaj zbio bez vanjskog utjecaja. Svjetlost u običnoj žarulji je generirana na ovakav način. U normalnim okolnostima srednje vrijeme života atoma u pobuđenom stanju, prije spontane emisije, je oko 10 -8 s. Međutim, za neka pobuđena stanja, ovo srednje vrijeme života može biti i do 105 puta veće. Takva stanja zovu se metastabilna stanja i igraju važnu ulogu u radu lasera. 12
Kako rade laseri (1) q q q Riječ laser je kratica engleskog izraza “light amplification by the stimulated emission of radiation”, što se prevodi kao “pojačanje svjetlosti stimuliranom emisijom radijacije”. Ovaj koncept je uveo Einstein 1917. godine, dok je prvi laser napravljen 1960. Razmotrimo izolirani atom koji može biti ili u svom osnovnom stanju (stanju s najnižom energijom) E 0, ili u pobuđenom stanju (stanju s višom energijom) Ex. Postoje tri različita fizikalna procesa kroz koje atom može prelaziti iz jednog u drugo stanje. 1. Apsorpcija. Atom se u početku nalazi u osnovnom stanju. Ako ga stavimo u elektromagnetsko polje frekvencije , atom može apsorbirati energiju h iz tog polja i preći u više energijsko stanja. Iz zakona sačuvanja energije imamo h =Ex-E 0. 2. Spontana emisija. Atom se na početku nalazi u pobuđenom stanju i nema vanjskog zračenja. Nakon nekog vremene, atom će spontano (“sam od sebe”) preći u osnovno stanje, emitirajući foton energije h. Ovaj proces zovemo spontana emisija, jer se događaj zbio bez vanjskog utjecaja. Svjetlost u običnoj žarulji je generirana na ovakav način. U normalnim okolnostima srednje vrijeme života atoma u pobuđenom stanju, prije spontane emisije, je oko 10 -8 s. Međutim, za neka pobuđena stanja, ovo srednje vrijeme života može biti i do 105 puta veće. Takva stanja zovu se metastabilna stanja i igraju važnu ulogu u radu lasera. 12
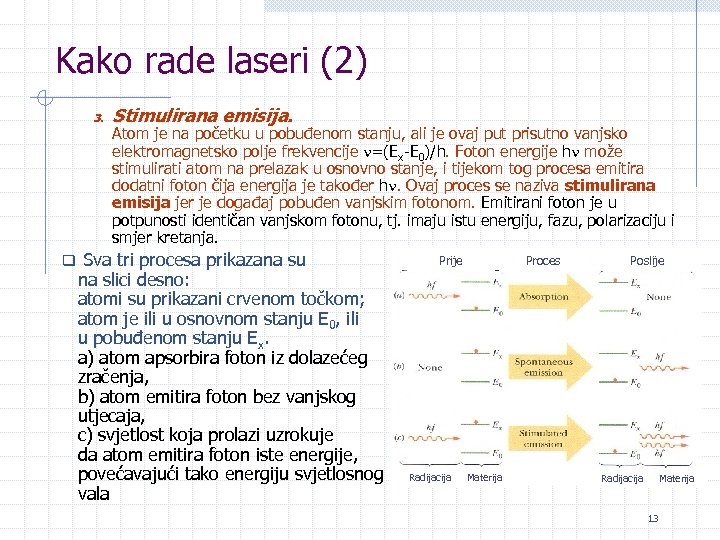 Kako rade laseri (2) 3. Stimulirana emisija. Atom je na početku u pobuđenom stanju, ali je ovaj put prisutno vanjsko elektromagnetsko polje frekvencije =(Ex-E 0)/h. Foton energije h može stimulirati atom na prelazak u osnovno stanje, i tijekom tog procesa emitira dodatni foton čija energija je također h. Ovaj proces se naziva stimulirana emisija jer je događaj pobuđen vanjskim fotonom. Emitirani foton je u potpunosti identičan vanjskom fotonu, tj. imaju istu energiju, fazu, polarizaciju i smjer kretanja. q Sva tri procesa prikazana su na slici desno: atomi su prikazani crvenom točkom; atom je ili u osnovnom stanju E 0, ili u pobuđenom stanju Ex. a) atom apsorbira foton iz dolazećeg zračenja, b) atom emitira foton bez vanjskog utjecaja, c) svjetlost koja prolazi uzrokuje da atom emitira foton iste energije, povećavajući tako energiju svjetlosnog vala Prije Radijacija Proces Materija Poslije Radijacija Materija 13
Kako rade laseri (2) 3. Stimulirana emisija. Atom je na početku u pobuđenom stanju, ali je ovaj put prisutno vanjsko elektromagnetsko polje frekvencije =(Ex-E 0)/h. Foton energije h može stimulirati atom na prelazak u osnovno stanje, i tijekom tog procesa emitira dodatni foton čija energija je također h. Ovaj proces se naziva stimulirana emisija jer je događaj pobuđen vanjskim fotonom. Emitirani foton je u potpunosti identičan vanjskom fotonu, tj. imaju istu energiju, fazu, polarizaciju i smjer kretanja. q Sva tri procesa prikazana su na slici desno: atomi su prikazani crvenom točkom; atom je ili u osnovnom stanju E 0, ili u pobuđenom stanju Ex. a) atom apsorbira foton iz dolazećeg zračenja, b) atom emitira foton bez vanjskog utjecaja, c) svjetlost koja prolazi uzrokuje da atom emitira foton iste energije, povećavajući tako energiju svjetlosnog vala Prije Radijacija Proces Materija Poslije Radijacija Materija 13
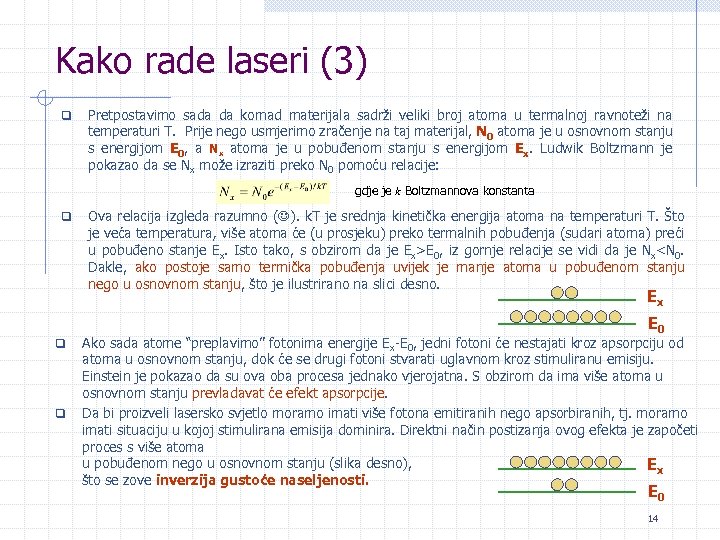 Kako rade laseri (3) q Pretpostavimo sada da komad materijala sadrži veliki broj atoma u termalnoj ravnoteži na temperaturi T. Prije nego usmjerimo zračenje na taj materijal, N 0 atoma je u osnovnom stanju s energijom E 0, a Nx atoma je u pobuđenom stanju s energijom Ex. Ludwik Boltzmann je pokazao da se Nx može izraziti preko N 0 pomoću relacije: gdje je k Boltzmannova konstanta q Ova relacija izgleda razumno ( ). k. T je srednja kinetička energija atoma na temperaturi T. Što je veća temperatura, više atoma će (u prosjeku) preko termalnih pobuđenja (sudari atoma) preći u pobuđeno stanje Ex. Isto tako, s obzirom da je Ex>E 0, iz gornje relacije se vidi da je Nx
Kako rade laseri (3) q Pretpostavimo sada da komad materijala sadrži veliki broj atoma u termalnoj ravnoteži na temperaturi T. Prije nego usmjerimo zračenje na taj materijal, N 0 atoma je u osnovnom stanju s energijom E 0, a Nx atoma je u pobuđenom stanju s energijom Ex. Ludwik Boltzmann je pokazao da se Nx može izraziti preko N 0 pomoću relacije: gdje je k Boltzmannova konstanta q Ova relacija izgleda razumno ( ). k. T je srednja kinetička energija atoma na temperaturi T. Što je veća temperatura, više atoma će (u prosjeku) preko termalnih pobuđenja (sudari atoma) preći u pobuđeno stanje Ex. Isto tako, s obzirom da je Ex>E 0, iz gornje relacije se vidi da je Nx
 Kako rade laseri (4) q q q - Plinski He-Ne zrcala laser S obzirom da inverzija gustoće naseljenosti nije konzistentna s termalnom ravnotežom, treba smisliti pametan način kako je postići i zadržati. Plinski He-Ne laseri daju svjetlost valne duljine 632, 8 nm. Rade na sljedećem principu: n Staklena cijev se napuni mješavinom He-Ne mješavinom plinova u odnosu 20: 80; neon je medij u kojemu se odvija fizikalni proces emisije laserskog svjetla. n Na slici desno je prikazan energijski dijagram za atome He i Ne. Struja koja prolazi kroz mješavinu plinova, kroz sudare atoma He i elektrona iz struje uzrokuju pobudu atoma helija u stanje E 3, koje je metastabilno. n Energija stanja helija E 3 (20, 61 e. V) je vrlo blizu energiji neonskog stanja E 2 (20, 66 e. V). Stoga, kada se atom helija u stanju E 3 sudari s atomom neona u osnovnom stanju E 0, energija pobude atoma helija se vrlo često prenese na atom neona, koji se pobudi u stanje E 2. Na ovaj način neonska energijska razina E 2 postane naseljenija elektronima od razine E 1 – imamo inverzuju gustoće naseljenosti. n Ovu inverziju gustoće naseljenosti je relativno lako izvesti zbog: (1) na početku je razina E 1 skoro potpuno prazna, (2) metastabilnost helijske razine E 3 osigurava kontinuirani prelaz atoma neona na razinu E 2 i (3) atomi iz razine E 1 vrlo brzo se vraćaju (preko međustanja koja nisu prikazana) u osnovno stanje E 0. 15
Kako rade laseri (4) q q q - Plinski He-Ne zrcala laser S obzirom da inverzija gustoće naseljenosti nije konzistentna s termalnom ravnotežom, treba smisliti pametan način kako je postići i zadržati. Plinski He-Ne laseri daju svjetlost valne duljine 632, 8 nm. Rade na sljedećem principu: n Staklena cijev se napuni mješavinom He-Ne mješavinom plinova u odnosu 20: 80; neon je medij u kojemu se odvija fizikalni proces emisije laserskog svjetla. n Na slici desno je prikazan energijski dijagram za atome He i Ne. Struja koja prolazi kroz mješavinu plinova, kroz sudare atoma He i elektrona iz struje uzrokuju pobudu atoma helija u stanje E 3, koje je metastabilno. n Energija stanja helija E 3 (20, 61 e. V) je vrlo blizu energiji neonskog stanja E 2 (20, 66 e. V). Stoga, kada se atom helija u stanju E 3 sudari s atomom neona u osnovnom stanju E 0, energija pobude atoma helija se vrlo često prenese na atom neona, koji se pobudi u stanje E 2. Na ovaj način neonska energijska razina E 2 postane naseljenija elektronima od razine E 1 – imamo inverzuju gustoće naseljenosti. n Ovu inverziju gustoće naseljenosti je relativno lako izvesti zbog: (1) na početku je razina E 1 skoro potpuno prazna, (2) metastabilnost helijske razine E 3 osigurava kontinuirani prelaz atoma neona na razinu E 2 i (3) atomi iz razine E 1 vrlo brzo se vraćaju (preko međustanja koja nisu prikazana) u osnovno stanje E 0. 15
 Kako rade laseri (5) q Plinski He-Ne laseri (nastavak) n Pretpostavite sada da se jedan foton spontano emitira prijelazu atoma neona iz E 2 u E 1. Takav foton može tada stimulirat emisiju istih takvih fotona, koji nadalje opet stimuliraju istu emisiju. . . Kroz takav proces stvara se koherentni snop crvene laserske svjetlosti koja putuje duž osi cijevi s plinom. Ako još na krajevima cijevi postavimo zrcala (s jedne strane nepropusno, a s drugo djelomično propusno) fotoni će se reflektirati od zrcala povećavajući tako vjerojatnost stimulirane emisije. Korisno lasersko svjetlo dobije se od dijela svjetlosti koja prođe kroz djelomično propusno zrcalo. 16
Kako rade laseri (5) q Plinski He-Ne laseri (nastavak) n Pretpostavite sada da se jedan foton spontano emitira prijelazu atoma neona iz E 2 u E 1. Takav foton može tada stimulirat emisiju istih takvih fotona, koji nadalje opet stimuliraju istu emisiju. . . Kroz takav proces stvara se koherentni snop crvene laserske svjetlosti koja putuje duž osi cijevi s plinom. Ako još na krajevima cijevi postavimo zrcala (s jedne strane nepropusno, a s drugo djelomično propusno) fotoni će se reflektirati od zrcala povećavajući tako vjerojatnost stimulirane emisije. Korisno lasersko svjetlo dobije se od dijela svjetlosti koja prođe kroz djelomično propusno zrcalo. 16
 Laseri s tri nivoa q Sistem ima 3 energijske razine. Izvor zračenja djeluje izvana i inducira (pumpa) prijelaze iz 1 3 f 13=(E 3 -E 1)/h. N 3 – pobuđeno stanje N 2 Stimulirani emisija N 1 q Ako je intenzitet vanjskog zračenja dovoljno velik, može s ostvariti jednaka naseljenost N 1 N 3. Kako se energijska razina N 3 raspada prije svega na N 2, omjer naseljenosti je q Za dovoljno veliku energijsku razliku između E 3 -E 2, naseljenost N 2 je veća od N 3 a time i od N 1, i tada je u dijelu prijelaza 1 -2 postignuta onverzija i frekvencija zarčenja f 12=(E 2 -E 1)/h postaje laserska frekvencija. 17
Laseri s tri nivoa q Sistem ima 3 energijske razine. Izvor zračenja djeluje izvana i inducira (pumpa) prijelaze iz 1 3 f 13=(E 3 -E 1)/h. N 3 – pobuđeno stanje N 2 Stimulirani emisija N 1 q Ako je intenzitet vanjskog zračenja dovoljno velik, može s ostvariti jednaka naseljenost N 1 N 3. Kako se energijska razina N 3 raspada prije svega na N 2, omjer naseljenosti je q Za dovoljno veliku energijsku razliku između E 3 -E 2, naseljenost N 2 je veća od N 3 a time i od N 1, i tada je u dijelu prijelaza 1 -2 postignuta onverzija i frekvencija zarčenja f 12=(E 2 -E 1)/h postaje laserska frekvencija. 17
 Laser – sistem s četri energijske razine q U laseru s tri razine više od polovice atoma mora biti u metastabilnom stanju da bi stimulirana bila stimulirana. To nije slučaj kod lasera s 4 razine. 4 3 1 Laserko svjetlo 2 q Prijelaz 1 -4 zasićen je frekvencijom pumpanja. Prijelaz 4 -3 osigurava inverziju naseljenosti za sistem 3 -2 (to je laserski prijelaz). Razina 2 se prazni u razinu 1 i time se psotiže da je niža razina laserskog prijelaza gotovo prazana. 18
Laser – sistem s četri energijske razine q U laseru s tri razine više od polovice atoma mora biti u metastabilnom stanju da bi stimulirana bila stimulirana. To nije slučaj kod lasera s 4 razine. 4 3 1 Laserko svjetlo 2 q Prijelaz 1 -4 zasićen je frekvencijom pumpanja. Prijelaz 4 -3 osigurava inverziju naseljenosti za sistem 3 -2 (to je laserski prijelaz). Razina 2 se prazni u razinu 1 i time se psotiže da je niža razina laserskog prijelaza gotovo prazana. 18
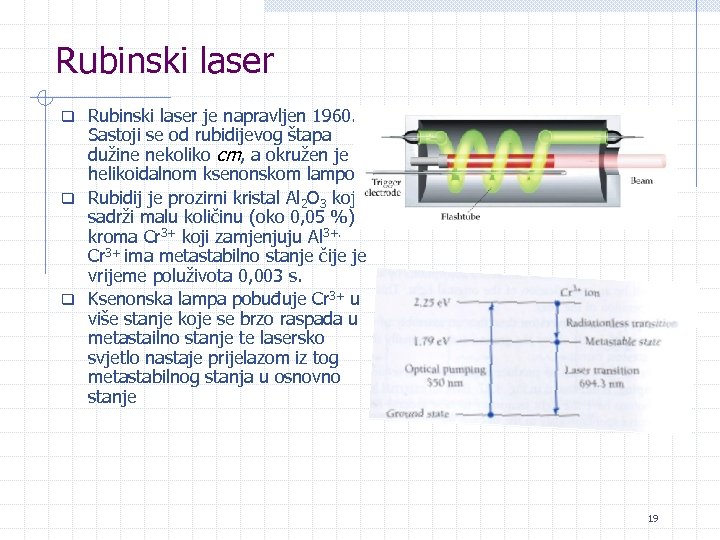 Rubinski laser q Rubinski laser je napravljen 1960. Sastoji se od rubidijevog štapa dužine nekoliko cm, a okružen je helikoidalnom ksenonskom lampom. q Rubidij je prozirni kristal Al 2 O 3 koji sadrži malu količinu (oko 0, 05 %) kroma Cr 3+ koji zamjenjuju Al 3+. Cr 3+ ima metastabilno stanje čije je vrijeme poluživota 0, 003 s. q Ksenonska lampa pobuđuje Cr 3+ u više stanje koje se brzo raspada u metastailno stanje te lasersko svjetlo nastaje prijelazom iz tog metastabilnog stanja u osnovno stanje 19
Rubinski laser q Rubinski laser je napravljen 1960. Sastoji se od rubidijevog štapa dužine nekoliko cm, a okružen je helikoidalnom ksenonskom lampom. q Rubidij je prozirni kristal Al 2 O 3 koji sadrži malu količinu (oko 0, 05 %) kroma Cr 3+ koji zamjenjuju Al 3+. Cr 3+ ima metastabilno stanje čije je vrijeme poluživota 0, 003 s. q Ksenonska lampa pobuđuje Cr 3+ u više stanje koje se brzo raspada u metastailno stanje te lasersko svjetlo nastaje prijelazom iz tog metastabilnog stanja u osnovno stanje 19
 Tipovi lasera q Laseri sa čvrstom tvari kao aktivnim sredstvom q q Najpoznatiji su rubinski laser, Yag laser itd. Plinski laseri, kojima je aktivno sredstvo neki plin Najpoznatiji su He-Ne i CO 2 -N laseri Poluvodički laseri, kojima je aktivno sredsto dioda (koriste se u telekomunikacijama i računalima) Kemijski laseri – u kojima je laserska emisija uzrokovana kemijskim procesom Laseri se mogu dijeliti i na: Kontinuirani laseri, koji daju neprekinute laserske snopove n Pulsni laseri, koji daju isprekidane laserske snopove q Najmanji laseri, koji se koriste pri prenosu podataka kroz svjetlovode mogu imati veličinu reda veličine mm i generirati malu snagu od npr. 200 m. W. q S druge strane najjači (i najveći) laseri koriste se u istraživanju nuklearne fuzije, astronomskim i vojnim aplikacijama. Takvi laseri mogu generirati kratke pulseve snage i do 1014 W, što je nekoliko stotina puta veće od ukupnog kapaciteta proizvodnje električne energije u SAD-u. Da se izbjegne kratkotrajni gubitak napajanja strujom u SAD-u, energija koja je potrebna za jedan puls se kontinuirano prikuplja u relativno dugim vremenskim intervalima između dva pulsa. n 20
Tipovi lasera q Laseri sa čvrstom tvari kao aktivnim sredstvom q q Najpoznatiji su rubinski laser, Yag laser itd. Plinski laseri, kojima je aktivno sredstvo neki plin Najpoznatiji su He-Ne i CO 2 -N laseri Poluvodički laseri, kojima je aktivno sredsto dioda (koriste se u telekomunikacijama i računalima) Kemijski laseri – u kojima je laserska emisija uzrokovana kemijskim procesom Laseri se mogu dijeliti i na: Kontinuirani laseri, koji daju neprekinute laserske snopove n Pulsni laseri, koji daju isprekidane laserske snopove q Najmanji laseri, koji se koriste pri prenosu podataka kroz svjetlovode mogu imati veličinu reda veličine mm i generirati malu snagu od npr. 200 m. W. q S druge strane najjači (i najveći) laseri koriste se u istraživanju nuklearne fuzije, astronomskim i vojnim aplikacijama. Takvi laseri mogu generirati kratke pulseve snage i do 1014 W, što je nekoliko stotina puta veće od ukupnog kapaciteta proizvodnje električne energije u SAD-u. Da se izbjegne kratkotrajni gubitak napajanja strujom u SAD-u, energija koja je potrebna za jedan puls se kontinuirano prikuplja u relativno dugim vremenskim intervalima između dva pulsa. n 20
 Primjene lasera (1) q Svakodnevna upotreba n n n n n Compact disc/DVD Laserski printer Optički diskovi (u skoroj budućnosti – npr. holografski diskovi) Bar-code čitači Zaštitni hologrami (na kreditnim karticama, Microsoftovom softwareu, vrijednosnim papirima) Prenos podataka svjetlovodima Direktni prijenos podataka (komunikacija među satelitima, vojna tehnologija) Hologrami (npr u muzejima, umjesto originalnih umjetnina) Laser show 3 D kinetičke skulpture 21
Primjene lasera (1) q Svakodnevna upotreba n n n n n Compact disc/DVD Laserski printer Optički diskovi (u skoroj budućnosti – npr. holografski diskovi) Bar-code čitači Zaštitni hologrami (na kreditnim karticama, Microsoftovom softwareu, vrijednosnim papirima) Prenos podataka svjetlovodima Direktni prijenos podataka (komunikacija među satelitima, vojna tehnologija) Hologrami (npr u muzejima, umjesto originalnih umjetnina) Laser show 3 D kinetičke skulpture 21
 Primjene lasera (2) q Vojne primjene n Mjerenje udaljenosti n Lociranje mete (navođenje “pametnih bombi”) n Laserska oružja (“Star Wars” program) n Osljepljivanje neprijatelja laserskim snopom q Medicinske primjene n Kirurgija w Operacije očiju, operacije zubi, dermatološki zahvati, opći zahvati n n Dijagnostika i liječenje raka Liječenje termičkim efektima (biostimulacija) q Industrija n Mjerenja n Povlačenje ultra ravnih linija n Procesiranje materijala w Rezanje, varenje, taljenje, isparavanje, fotolitografija u poluvodičkoj industriji. . . n Spektralna analiza 22
Primjene lasera (2) q Vojne primjene n Mjerenje udaljenosti n Lociranje mete (navođenje “pametnih bombi”) n Laserska oružja (“Star Wars” program) n Osljepljivanje neprijatelja laserskim snopom q Medicinske primjene n Kirurgija w Operacije očiju, operacije zubi, dermatološki zahvati, opći zahvati n n Dijagnostika i liječenje raka Liječenje termičkim efektima (biostimulacija) q Industrija n Mjerenja n Povlačenje ultra ravnih linija n Procesiranje materijala w Rezanje, varenje, taljenje, isparavanje, fotolitografija u poluvodičkoj industriji. . . n Spektralna analiza 22
 Primjene lasera (3) q Istraživačke svrhe n Fundamentalna istraživanja w Interakcija zračenja s materijom, genetski inženjering. . . n n Spektroskopija Nuklearna fuzija Hlađenje atoma na ultra niske tempereture Generiranje vrlo kratkih pulseva za studiranje vrlo brzih procesa q Posebne primjene n n n Prijenos energije (u budućim svemirskim postajama) Laserski žiroskop (instrument za orijentaciju u prostoru) Laserski procesi direktno u svjetlovodu (primjena u telekomunikacijama) q Više o pojedinoj primjeni možete naći na http: //stwi. weizmann. ac. il/Lasers/laserweb/Apps/Fap_spec. htm 23
Primjene lasera (3) q Istraživačke svrhe n Fundamentalna istraživanja w Interakcija zračenja s materijom, genetski inženjering. . . n n Spektroskopija Nuklearna fuzija Hlađenje atoma na ultra niske tempereture Generiranje vrlo kratkih pulseva za studiranje vrlo brzih procesa q Posebne primjene n n n Prijenos energije (u budućim svemirskim postajama) Laserski žiroskop (instrument za orijentaciju u prostoru) Laserski procesi direktno u svjetlovodu (primjena u telekomunikacijama) q Više o pojedinoj primjeni možete naći na http: //stwi. weizmann. ac. il/Lasers/laserweb/Apps/Fap_spec. htm 23


