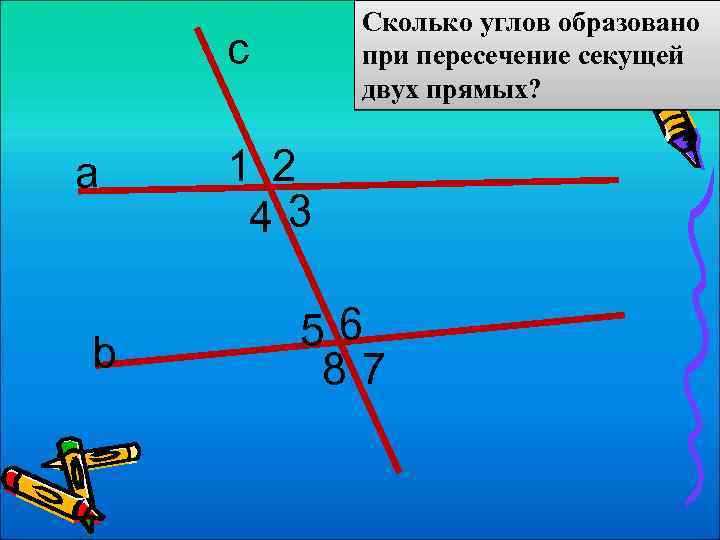
Сколько углов образовано при пересечение секущей двух прямых? с а b 1 2 43 56 87
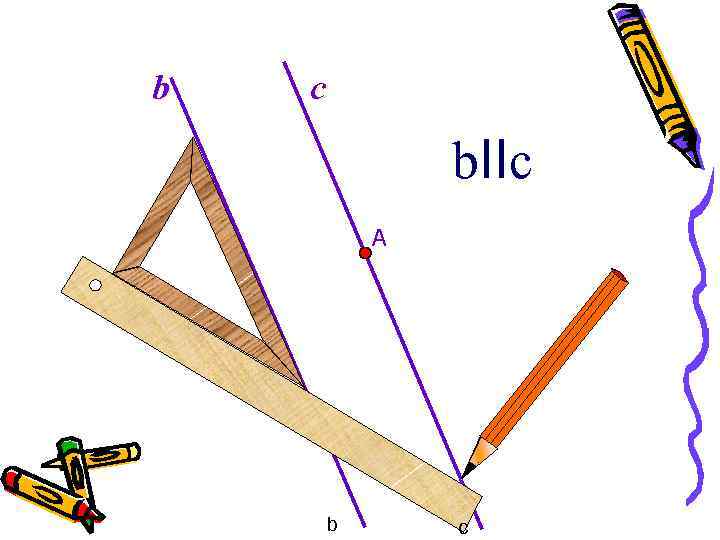
b c b. IIc А b c
Аксиома параллельных прямых
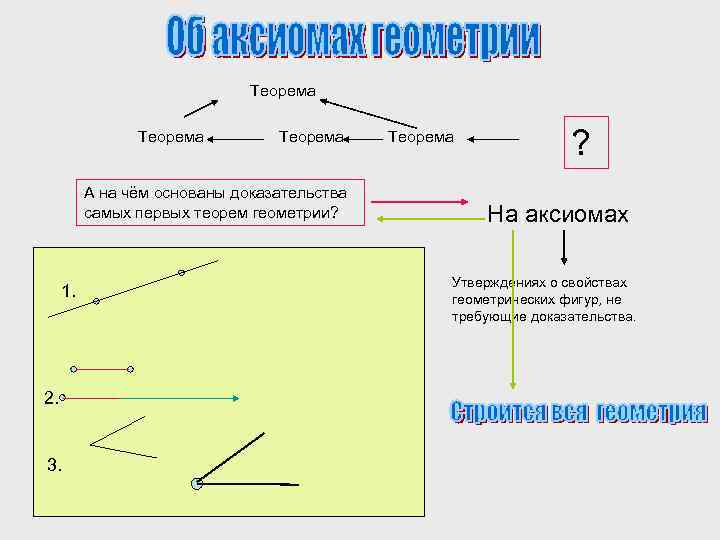
Теорема А на чём основаны доказательства самых первых теорем геометрии? 1. 2. 3. Теорема ? На аксиомах Утверждениях о свойствах геометрических фигур, не требующие доказательства.
Сначала формулируются исходные положения аксиомы На их основе, путём логических рассуждений доказываются другие утверждения Такой подход к построению геометрии зародился в глубокой древности и был изложен в сочинении «Начала» древнегреческого учёного Евклида Геометрия, изложенная в «Началах» , называется евклидовой геометрией Некоторые из аксиом Евклида (часть из них он называл постулатами) и сейчас используются в геометрии 365 – 300 гг. до н. э. Слово «аксиома» происходит от греческого «аксиос» , что означает «ценный, достойный» .
М в с в а Дано: а, М а Доказать: можно провести прямую через М а Доказательство: 1. Проведем с ┴ а 2. в ┴ с Сколько прямых можно провести через точку М параллельных а?
Нам представляется, что через т. М нельзя провести прямую (отличную от прямой в), параллельную прямой а. А можем ли мы это доказать? Ответ на этот непростой вопрос дал великий русский математик Н. И. Лобачевский. Он выяснил, что это утверждение доказать нельзя, т. к. само является аксиомой.
Через точку, не лежащую на прямой проходит только одна прямая параллельная данной. Следствие – это утверждение, которое выводится непосредственно из аксиом и теорем.
Сл-е 1: Если прямая пересекает одну из двух параллельных прямых, то она пересекает М и другую. с а в Доказательство: (методом от противного) 1. Предположим, что прямая с не пересекает прямую в, значит, с параллельно в. 2. Тогда через т. М проходят две прямые а и с параллельные прямой в. 3. Но это противоречит аксиоме параллельных прямых, значит, прямая с пересекает прямую в.
Сл-е 2: Если две прямые параллельны третьей прямой, то они параллельны. а в с Доказательство: (метод от противного) 1. Предположим, что прямая а и прямая в пересекаются. 2. Тогда через т. М проходят две прямые а и в параллельные прямой с 3. Но это противоречит аксиоме параллельных прямых. 4. Значит прямые а и в параллельны.
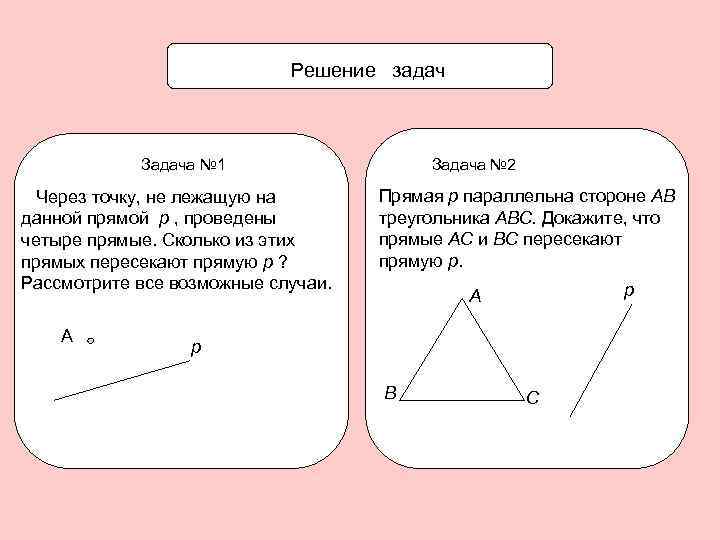
Решение задач Задача № 2 Задача № 1 Через точку, не лежащую на данной прямой p , проведены четыре прямые. Сколько из этих прямых пересекают прямую p ? Рассмотрите все возможные случаи. А Прямая р параллельна стороне АВ треугольника АВС. Докажите, что прямые АС и ВС пересекают прямую р. р А р В С
Скачать презентацию Сколько углов образовано при пересечение секущей двух прямых
Аксиома параллельных прямых.ppt