Скачать презентацию Скалярные и векторные поля Градиент скалярного поля Скачать презентацию Скалярные и векторные поля Градиент скалярного поля

MMF_L4.ppt

  • Количество слайдов: 32

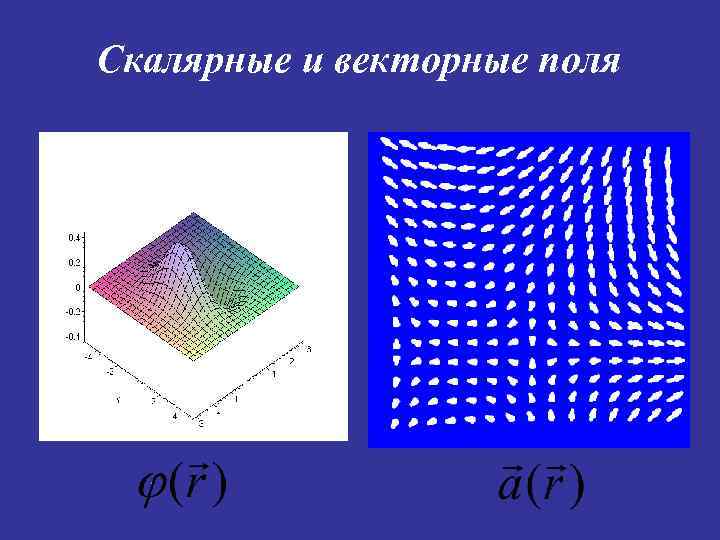Скалярные и векторные поля Скалярные и векторные поля

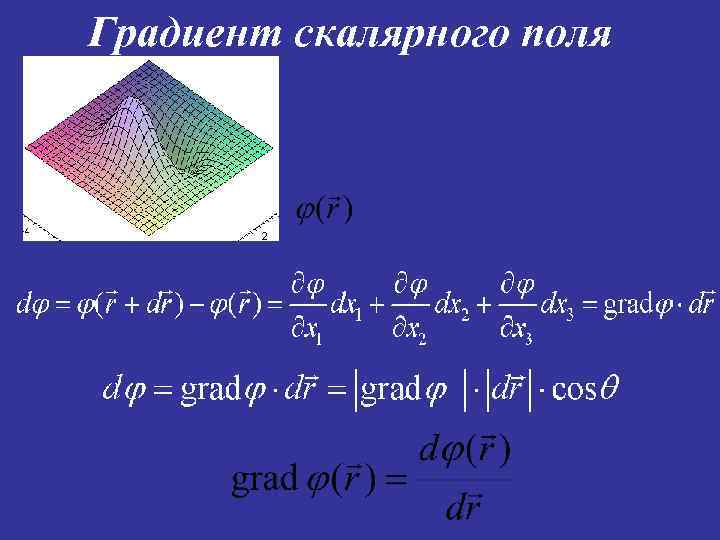Градиент скалярного поля Градиент скалярного поля

Градиент скалярного поля Направление вектора grad j – это направление скорейшего роста скалярного поля Градиент скалярного поля Направление вектора grad j – это направление скорейшего роста скалярного поля в данной точке, а модуль градиента – это скорость роста поля в этом направлении.

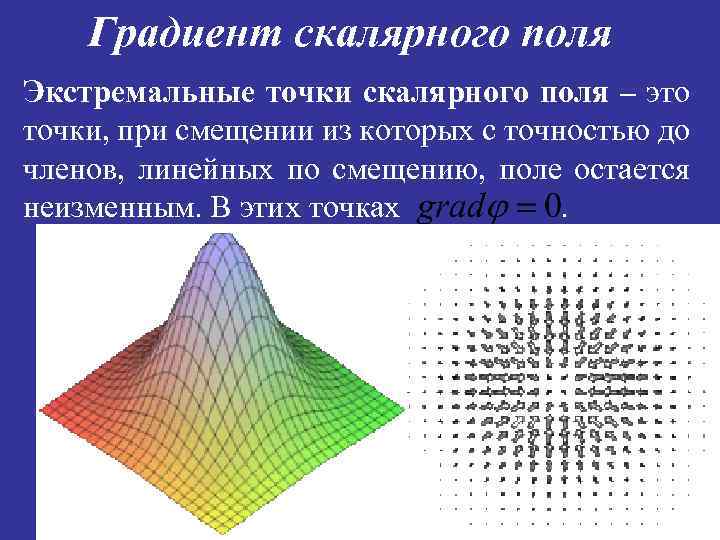Градиент скалярного поля Экстремальные точки скалярного поля – это точки, при смещении из которых Градиент скалярного поля Экстремальные точки скалярного поля – это точки, при смещении из которых с точностью до членов, линейных по смещению, поле остается неизменным. В этих точках.

Градиент скалярного поля Силовое поле – это векторное поле, значение которого в каждой точке Градиент скалярного поля Силовое поле – это векторное поле, значение которого в каждой точке пространства равно силе, действующей на частицу в этой точке. Потенциальное (или безвихревое) силовое поле – это силовое поле, работа по перемещению частицы в котором по любому замкнутому контуру равна нулю. В этом случае можно ввести скалярное поле потенциальной энергии , связанное с силовым полем соотношением:

Градиент скалярного поля Градиент скалярного поля

Градиент скалярного поля Плотность потока тепла – количество тепловой энергии, протекающей в единицу времени Градиент скалярного поля Плотность потока тепла – количество тепловой энергии, протекающей в единицу времени через единичную площадку, ориентированную перпендикулярно потоку тепла. Вектор плотности потока тепла связан с градиентом температуры соотношением: , где – скалярное поле температуры, k - коэффициент теплопроводности.

Дивергенция векторного поля Вектор площадки направлен перпендикулярно площадке и равен по модулю ее площади. Дивергенция векторного поля Вектор площадки направлен перпендикулярно площадке и равен по модулю ее площади. Этот вектор направлен по внешней нормали , если площадка является элементом замкнутой поверхности, в противном случае считается, что этот вектор связан с направлением обхода площадки правилом правого винта.

Дивергенция векторного поля Поток вектора DФ векторного поля через площадку в точке равен Дивергенция векторного поля Поток вектора DФ векторного поля через площадку в точке равен

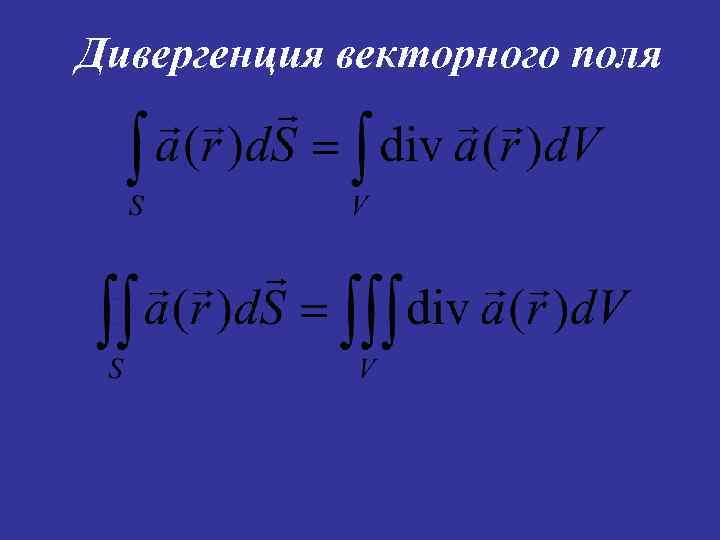Дивергенция векторного поля Дивергенция векторного поля

Дивергенция векторного поля Дивергенция векторного поля

Дивергенция векторного поля Дивергенция векторного поля

Дивергенция векторного поля Уравнение непрерывности – дифференциальное уравнение в частных производных, связывающее скорость изменения Дивергенция векторного поля Уравнение непрерывности – дифференциальное уравнение в частных производных, связывающее скорость изменения плотности жидкости в каждой точке объема и дивергенцию произведения плотности и скорости жидкости в этой же точке: . Уравнение непрерывности выводится из закона сохранения массы с использованием теоремы Гаусса.

Дивергенция векторного поля Закон сохранения электрического заряда в дифференциальной форме – дифференциальное уравнение в Дивергенция векторного поля Закон сохранения электрического заряда в дифференциальной форме – дифференциальное уравнение в частных производных, связывающее скорость изменения плотности электрического заряда в каждой точке и дивергенцию плотности электрического тока в этой же точке: . Выводится из закона сохранения заряда с использованием теоремы Гаусса.

Дивергенция векторного поля Уравнение теплопроводности – дифференциальное уравнение для температуры, которое выводится с использованием Дивергенция векторного поля Уравнение теплопроводности – дифференциальное уравнение для температуры, которое выводится с использованием теоремы Гаусса из закона сохранения тепловой энергии в процессах теплопередачи. В однородной среде уравнение теплопроводности имеет вид: где c – коэффициент теплопроводности.

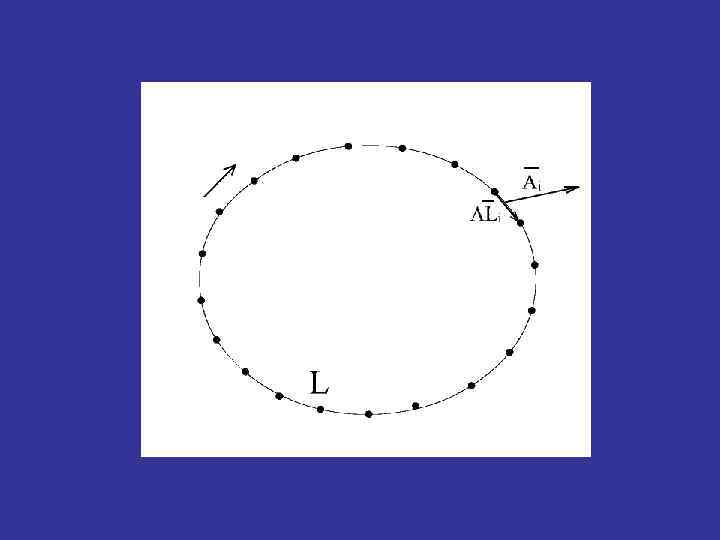
Ротор векторного поля Циркуляция AL векторного поля по замкнутому контуру L - скалярная величина, Ротор векторного поля Циркуляция AL векторного поля по замкнутому контуру L - скалярная величина, равная сумме скалярных произведений векторов участков , на которые разбит конур L, и векторов в средних точках этих участков: Циркуляция меняет знак при изменении направления обхода контура.

Ротор векторного поля Циркуляцию по контуру L можно представить в виде суммы циркуляций по Ротор векторного поля Циркуляцию по контуру L можно представить в виде суммы циркуляций по границам Lk малых площадок , на которые разбита поверхность S, натянутая на контур L, причем направление векторов согласуется правилом правого винта с направлением обхода контуров L и Lk, для которых вычисляются циркуляции:

Ротор векторного поля Чтобы записанная сумма была интегрируемой, необходимо, чтобы суммируемые величины были пропорциональны. Ротор векторного поля Чтобы записанная сумма была интегрируемой, необходимо, чтобы суммируемые величины были пропорциональны. Это возможно, если существует векторное поле, называемое ротором такое, что.

Ротор векторного поля Таким образом, циркуляция может быть записана как в виде интеграла по Ротор векторного поля Таким образом, циркуляция может быть записана как в виде интеграла по контуру, так и в виде потока ротора векторного поля через поверхность, натянутую на контур. Этот результат называется теоремой Стокса: Положительное направление нормали для поверхности должно быть связано с направлением обхода контура по правилу правого винта.

Ротор векторного поля частные производные соотношением: выражается компонент через поля . Определитель, стоящий в Ротор векторного поля частные производные соотношением: выражается компонент через поля . Определитель, стоящий в правой части, надо формально разложить по первой строке, что дает выражение для ротора в виде линейной комбинации единичных ортов:

Ротор векторного поля Ротор векторного поля

Ротор векторного поля Ротор векторного поля

Ротор векторного поля Векторное поле называется соленоидальным, если поток его через любую замкнутую поверхность Ротор векторного поля Векторное поле называется соленоидальным, если поток его через любую замкнутую поверхность равен нулю: Если это условие выполняется подобластей некоторой области условие равносильно тому, что дивергенция векторного поля для любых W, то это равна нулю :

Ротор векторного поля Для широкого класса областей W, это условие выполняется тогда и только Ротор векторного поля Для широкого класса областей W, это условие выполняется тогда и только тогда, когда a имеет векторный потенциал A, то есть

Ротор векторного поля Ротор векторного поля

Оператор “набла” Векторный дифференциальный оператор «набла» имеет компоненты Алгебраические преобразования выражений, содержащих оператор «набла» Оператор “набла” Векторный дифференциальный оператор «набла» имеет компоненты Алгебраические преобразования выражений, содержащих оператор «набла» , проводятся по обычным правилам векторной алгебры, надо только учитывать, что «набла» - это дифференциальный оператор и по определению он должен стоять слева от функции, которую нужно продифференцировать.

Оператор “набла” Так – это дивергенция поля, а – скалярный дифференциальный оператор: Оператор “набла” Так – это дивергенция поля, а – скалярный дифференциальный оператор:

Оператор “набла” Вместо операций grad, div, rot вводим операции с использованием оператора набла: Оператор “набла” Вместо операций grad, div, rot вводим операции с использованием оператора набла:

Оператор “набла” Вместо операций grad, div, rot вводим операции с использованием оператора набла: Оператор “набла” Вместо операций grad, div, rot вводим операции с использованием оператора набла:

Оператор Лапласа – скалярный дифференциальный оператор второго порядка: Оператор Лапласа – скалярный дифференциальный оператор второго порядка:

Оператор Лапласа – скалярный дифференциальный оператор второго порядка: Оператор Лапласа – скалярный дифференциальный оператор второго порядка: