 Скалярное произведение векторов. Разложение вектора по двум не коллинеарным векторам
Скалярное произведение векторов. Разложение вектора по двум не коллинеарным векторам
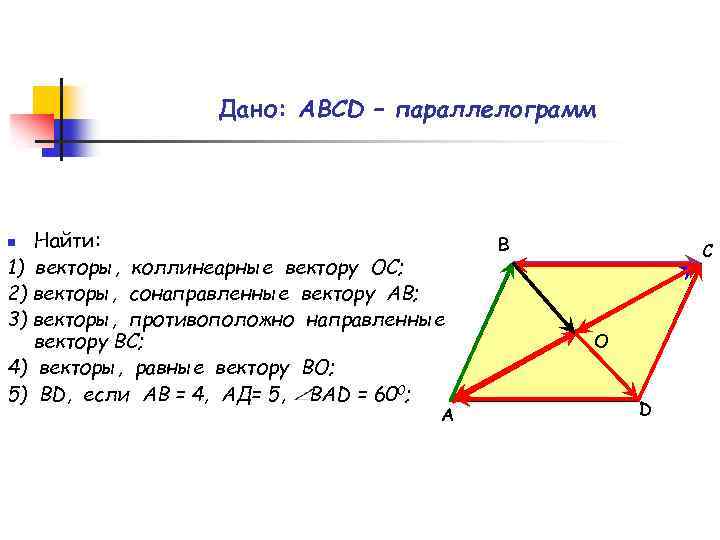 Дано: АВСD – параллелограмм Найти: 1) векторы, коллинеарные вектору ОС; 2) векторы, сонаправленные вектору АВ; 3) векторы, противоположно направленные вектору ВС; 4) векторы, равные вектору ВО; 5) ВD, если АВ = 4, АД= 5, ВАD = 600; n А В С О D
Дано: АВСD – параллелограмм Найти: 1) векторы, коллинеарные вектору ОС; 2) векторы, сонаправленные вектору АВ; 3) векторы, противоположно направленные вектору ВС; 4) векторы, равные вектору ВО; 5) ВD, если АВ = 4, АД= 5, ВАD = 600; n А В С О D
 Угол между векторами. А О В
Угол между векторами. А О В
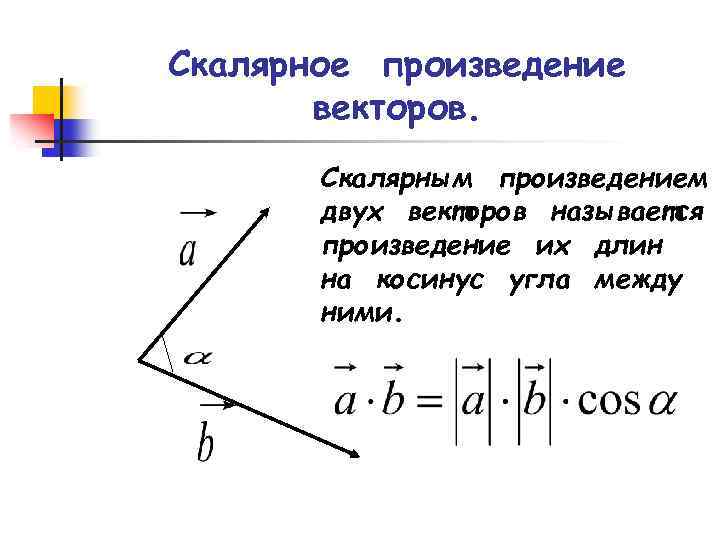 Скалярное произведение векторов. Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
Скалярное произведение векторов. Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
 Если , то Скалярное произведение называется скалярным квадратом вектора
Если , то Скалярное произведение называется скалярным квадратом вектора
 Теорема: Любой вектор можно разложить по двум данным неколлинеарным векторам, причём коэффициенты разложения определяются единственным образом.
Теорема: Любой вектор можно разложить по двум данным неколлинеарным векторам, причём коэффициенты разложения определяются единственным образом.
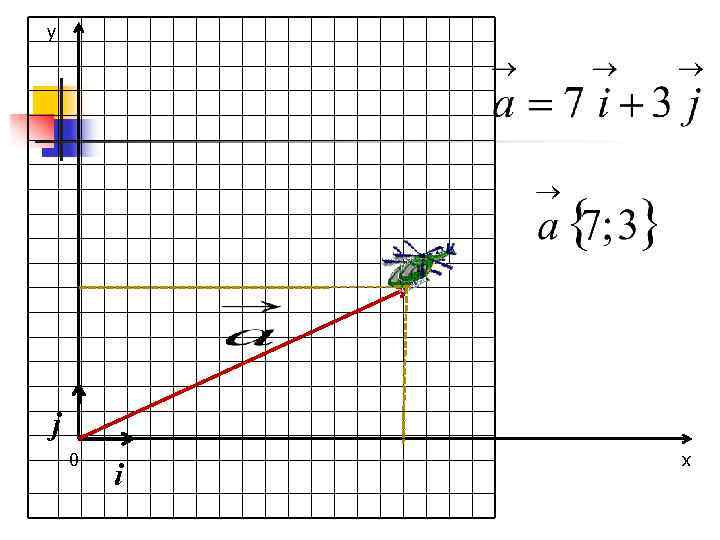 y j 0 i x
y j 0 i x
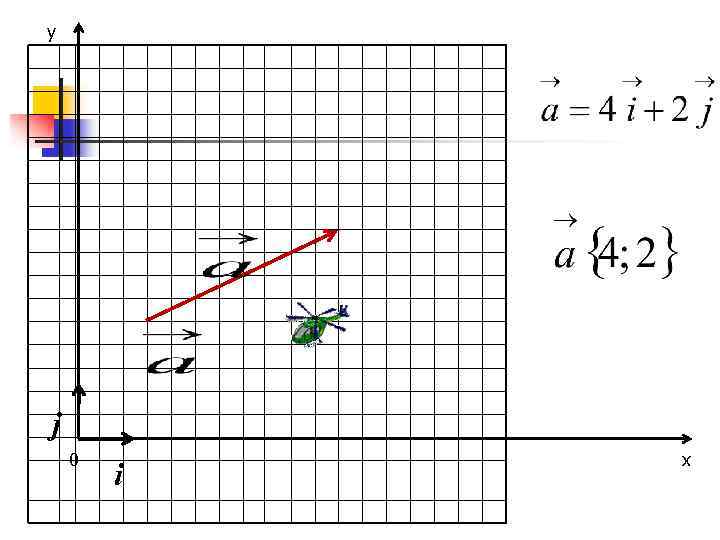 y j 0 i x
y j 0 i x
 10. Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. а+b=(х1+х2)i + (у1+у2)j 20. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. а-b=(х1 -х2)i + (у1 -у2)j 30. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. ка =кхi +куj
10. Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. а+b=(х1+х2)i + (у1+у2)j 20. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. а-b=(х1 -х2)i + (у1 -у2)j 30. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. ка =кхi +куj