Size effect in the vortex-matter phase transition in

Size effect in the vortex-matter phase transition in Bi 2 Sr 2 Ca. Cu. O 8+ ? B. Kalisky, A. Shaulov and Y. Yeshurun T. Tamegai Bar-Ilan University Israel University of Tokyo Vortex Matter Workshop, Mombay, India February 2005

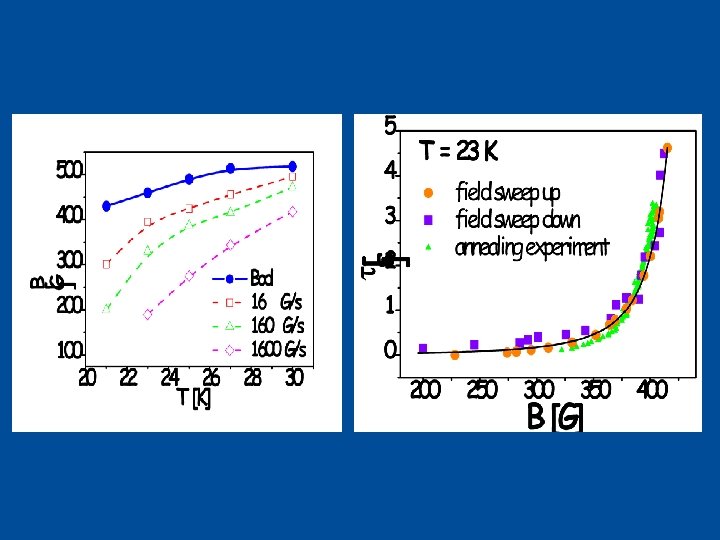
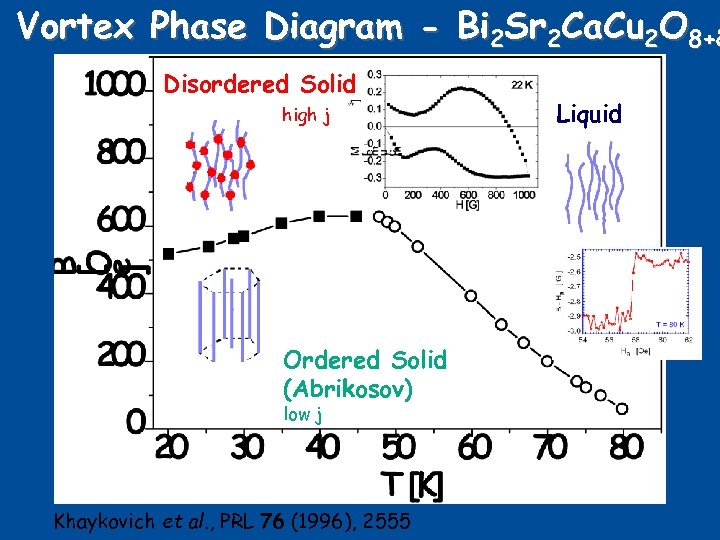Vortex Phase Diagram - Bi 2 Sr 2 Ca. Cu 2 O 8+d Disordered Solid high j Ordered Solid (Abrikosov) low j Khaykovich et al. , PRL 76 (1996), 2555 Liquid

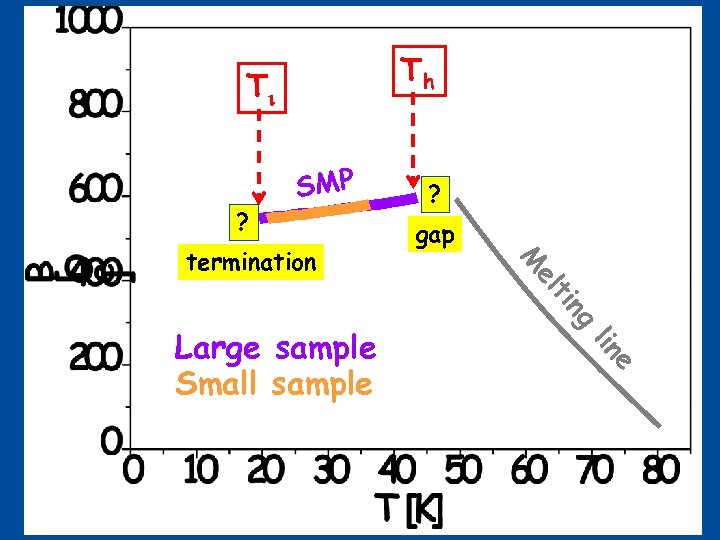Disordered Solid T high j j high ? SMP ? gap ng ng ng ti ti ti el el el e e e lin lin Large sample Solid Ordered Small sample (Abrikosov) low j Liquid M M M termination Th

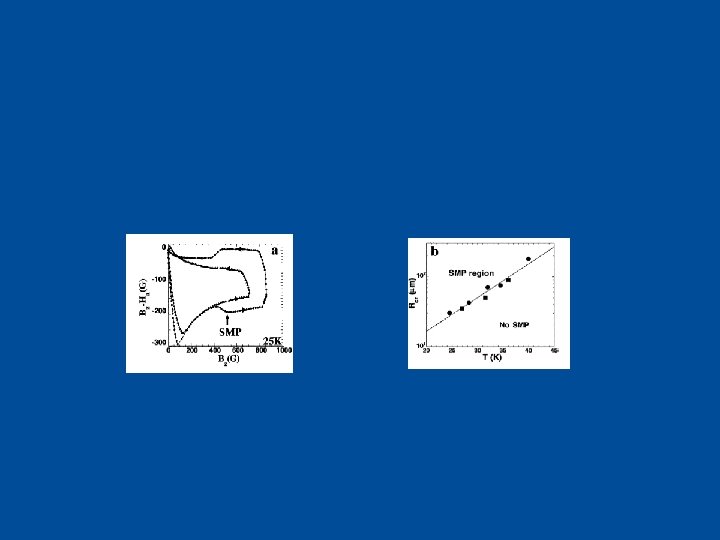
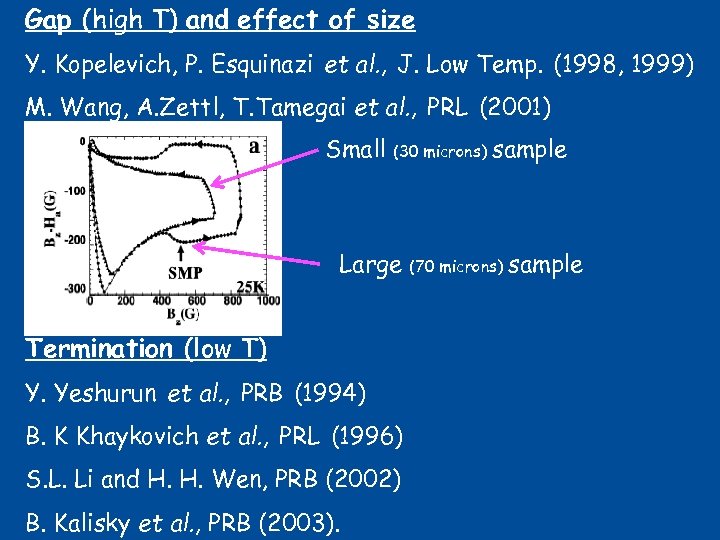Gap (high T) and effect of size Y. Kopelevich, P. Esquinazi et al. , J. Low Temp. (1998, 1999) M. Wang, A. Zettl, T. Tamegai et al. , PRL (2001) Small (30 microns) Large Termination (low T) Y. Yeshurun et al. , PRB (1994) B. K Khaykovich et al. , PRL (1996) S. L. Li and H. H. Wen, PRB (2002) B. Kalisky et al. , PRB (2003). sample (70 microns) sample

Goals of this talk 1. Explain the origin of : • Gap - high T • Termination - low T 2. Understand the role of sample size

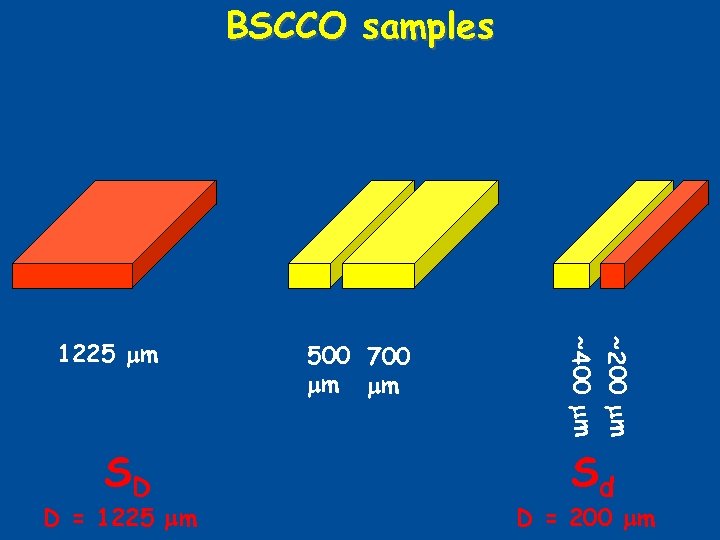BSCCO samples SD D = 1225 mm 500 700 mm mm ~200 mm ~400 mm 1225 mm Sd D = 200 mm

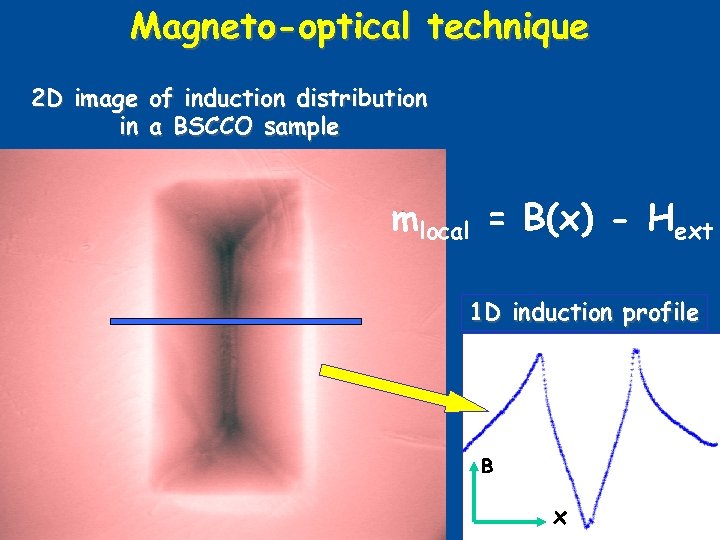Magneto-optical technique 2 D image of induction distribution in a BSCCO sample mlocal = B(x) - Hext 1 D induction profile B B x

M vs. B at different T The SMP decreases with temperature

Peak height vs. T at 4 G/s Peak height = m from onset to peak SD T h Sd Large sample still demonstrates SMP at 27 K

m vs. B, different field sweep rates SMP increases with SR

Peak height vs. field sweep rate, 27 K Increase of peak height with sweep rate is a result of increase in the persistent current due to shorter time window of the experiment

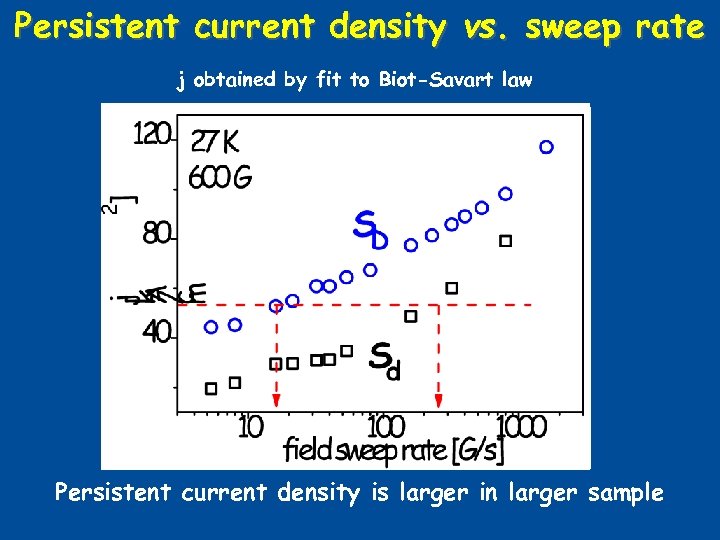Persistent current density vs. sweep rate j obtained by fit to Biot-Savart law Persistent current density is larger in larger sample

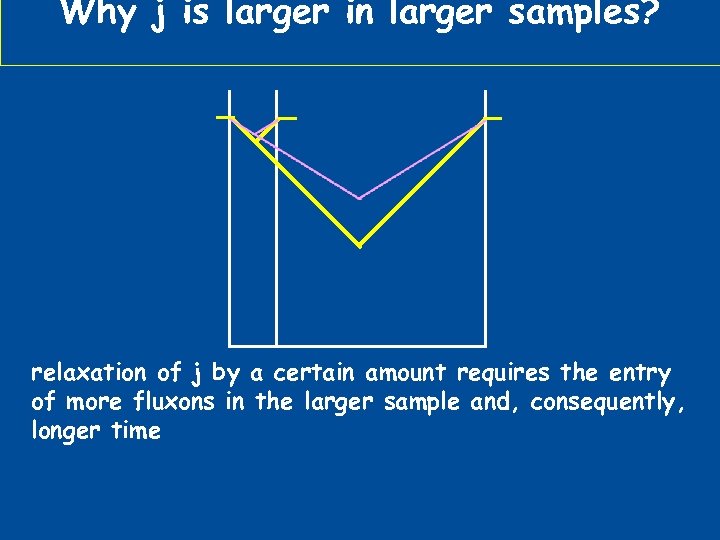Why j is larger in larger samples? relaxation of j by a certain amount requires the entry of more fluxons in the larger sample and, consequently, longer time

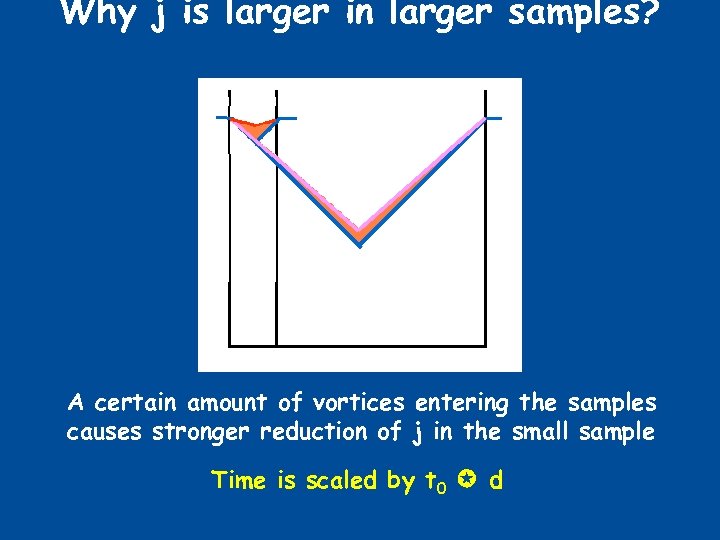Why j is larger in larger samples? A certain amount of vortices entering the samples causes stronger reduction of j in the small sample Time is scaled by t 0 d

Calculation of the size dependence of j in SR experiments SR and d appear only in the integration constant and boundary conditions

Numerically calculated j/jc vs. SR Hext = 1000 G n=3 jc=106 A/cm 2 • j increases with SR • j increases with the sample size • Results are qualitatively similar to experimental results

Summary of behavior at high temperatures Decay of persistent currents Disappearance of SMP above Th Small samples: Faster relaxation Disappearance of SMP at lower Th In comparing samples of different size, one should compensate for the reduction in the persistent current in the smaller samples by, e. g. , adjusting the field SR

Effect of field sweep rate on the peak height at different T 27 K – peak height increases with SR 21 K – peak height decreases with SR maximum in the peak height at intermediate SR

Transient Disordered Vortex States (TDVS) TDVS are injected through the sample edges Disorder is induced by inhomogeneous surface barriers Hext Paltiel, Zeldov et al. , Nature 403, 398 (2000). “Edge contamination” j h- hig Bod Appearance of TVS low -j Short As sweep rate increases, TVS with shorter lifetime play a role

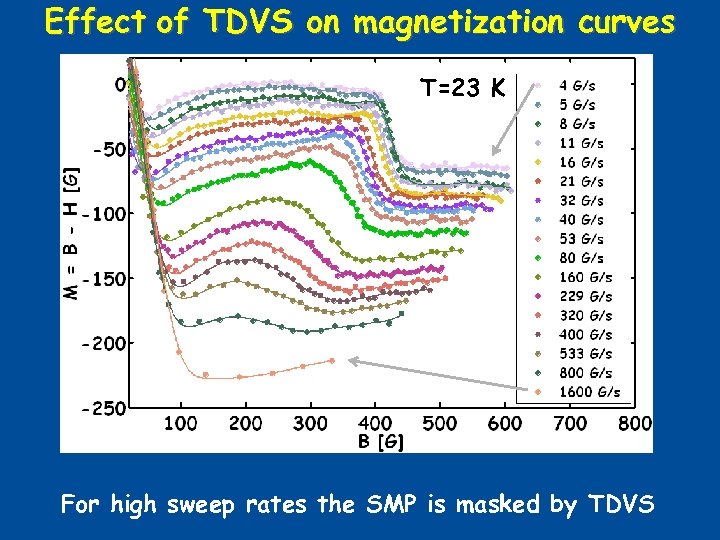Effect of TDVS on magnetization curves T=23 K For high sweep rates the SMP is masked by TDVS

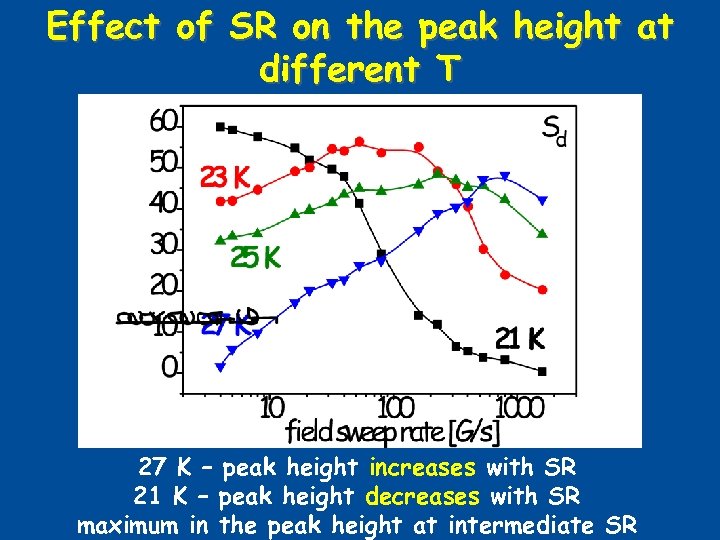Effect of SR on the peak height at different T 27 K – peak height increases with SR 21 K – peak height decreases with SR maximum in the peak height at intermediate SR

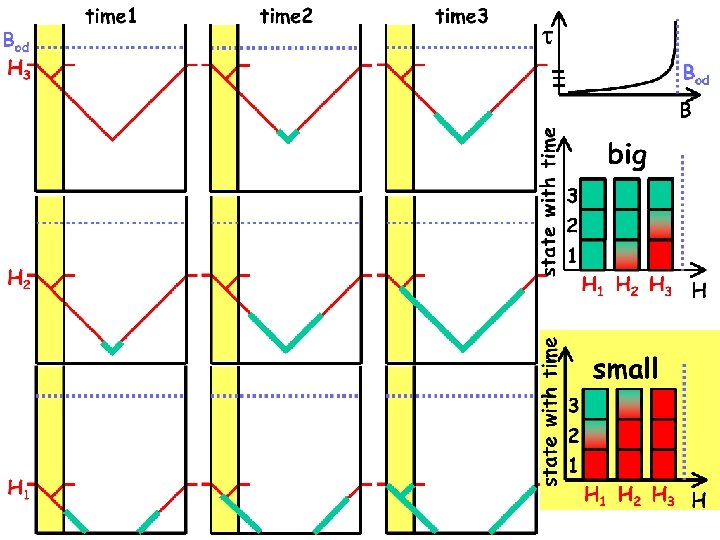
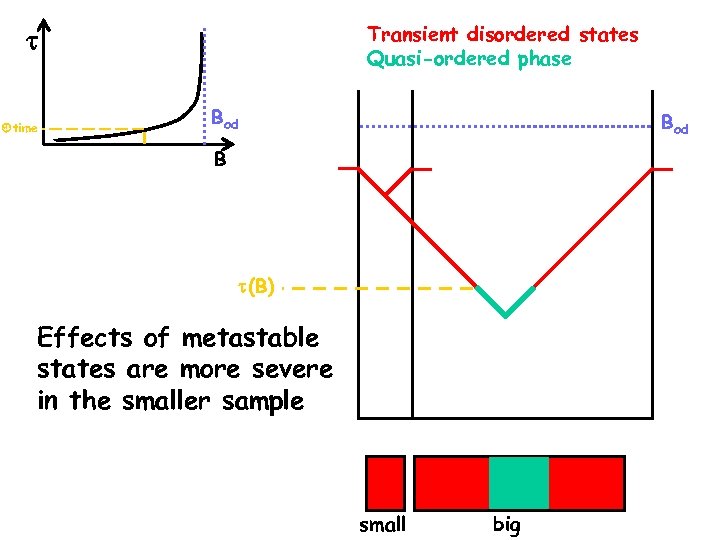Transient disordered states Quasi-ordered phase time Bod B (B) Effects of metastable states are more severe in the smaller sample Effects vortex state of states small big

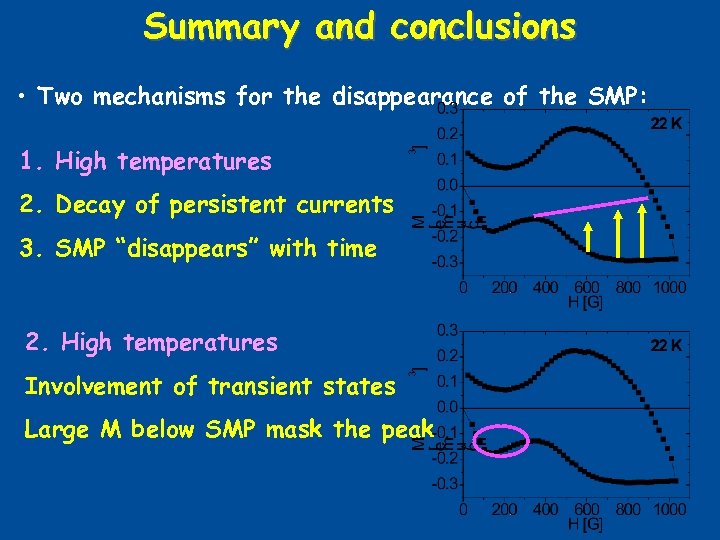Summary and conclusions • Two mechanisms for the disappearance of the SMP: 1. High temperatures 2. Decay of persistent currents 3. SMP “disappears” with time 2. High temperatures Involvement of transient states Large M below SMP mask the peak

Summary and conclusions (cont. ) • Sample size plays an important role: 1. Relaxation rate 2. Relative contribution of TDVS are enhanced in smaller samples T and Th depend on sample size

Summary and conclusions (cont. ) • Compensate experimentally for these effects : 1. Increasing SR - high T 2. Decreasing SR - low T Our results question previous reports on size effect in the vortex matter phase transition

Peak height vs. SR at 25 K The maximum widens for the larger sample The SMP in the larger sample is less affected by relaxation of j and by the engagement of metastable states, for low and high field sweep rates

BSCCO samples D = 1225 mm 670 750 mm Sd ~400 mm SD 520 460 mm ~200 mm 1225 mm D = 200 mm

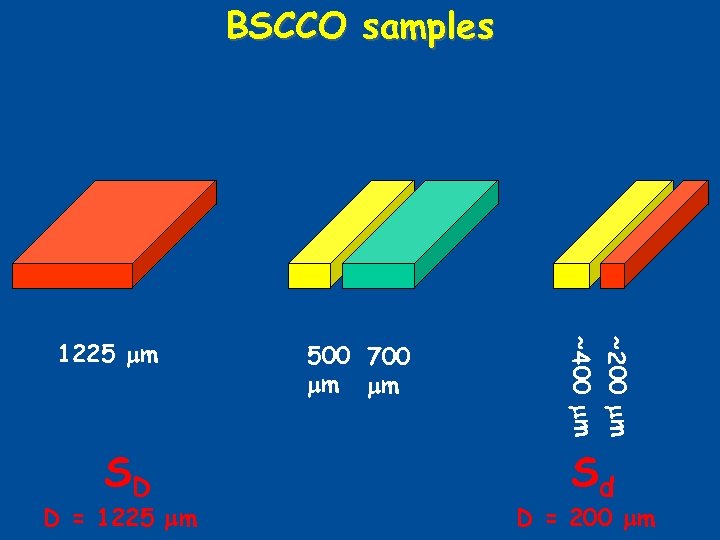BSCCO samples SD D = 1225 mm 500 700 mm mm ~200 mm ~400 mm 1225 mm Sd D = 200 mm

Introduction The sample size plays important role in superconductors, since the basic quantity, the magnetization, depends on sample size. Unlike in ferromagnetic materials, where the basic quantity is an intrinsic or uniform volume property.

Effect of size in superconductors • Tc ? ? ? [ ? ? ? ] • Irreversibility line [ ? ? ? ] • Critical current density [Qin 2004] • Magnetic properties like relaxation rates [Weir 1991, ? ? ? 0000 , Yafit 2004] • What else ? ? ? • The SMP disappears in samples with reduced size [Esquinazi 1998, Wang 2001] => The order-disorder phase transition depends on sample size => “size effect” in SC

קישור לשקף הבא We start with the lower termination – below Tl.

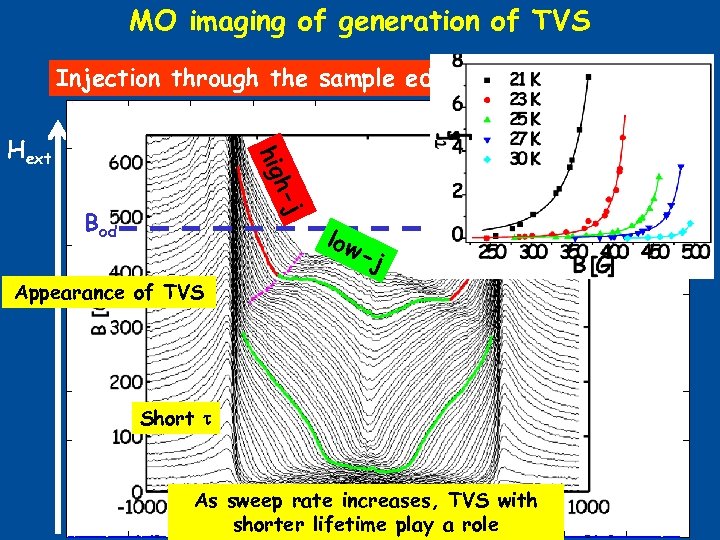MO imaging of generation of TVS Injection through the sample edges j h- hig Disorder is induced by inhomogeneous surface barriers Hext Paltiel, Zeldov et al. , Nature 403, 398 (2000). “Edge contamination” Bod low -j Appearance of TVS Short As sweep rate increases, TVS with shorter lifetime play a role

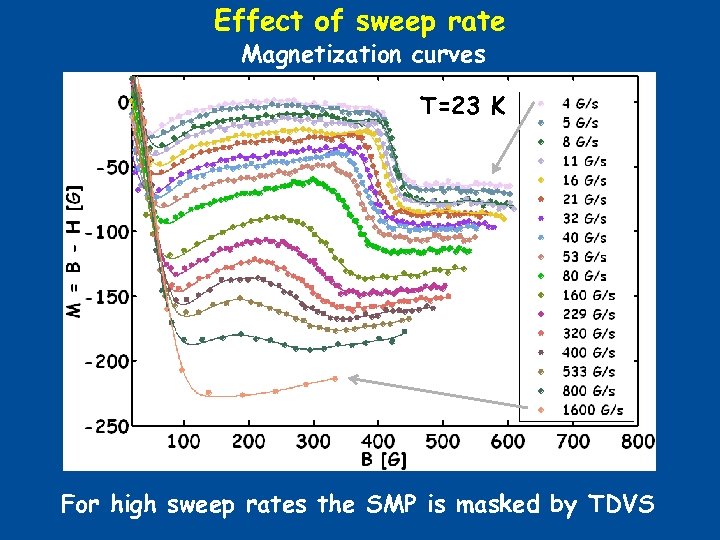Effect of sweep rate Magnetization curves T=23 K For high sweep rates the SMP is masked by TDVS

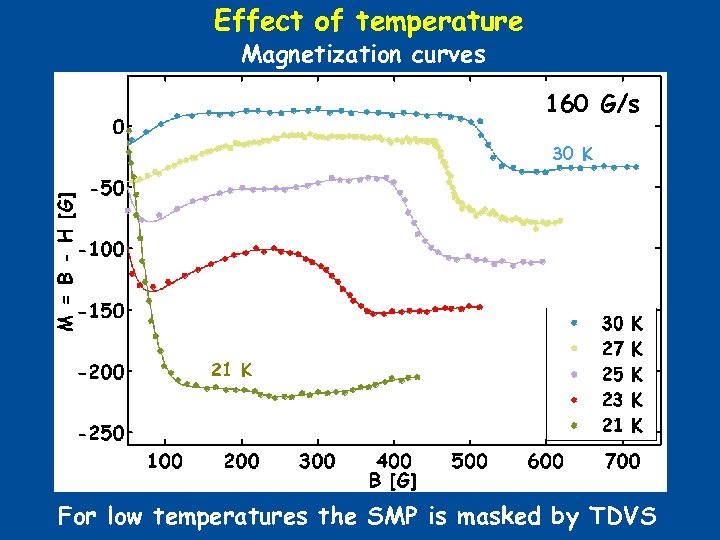Effect of temperature Magnetization curves 160 G/s 30 K 21 K For low temperatures the SMP is masked by TDVS

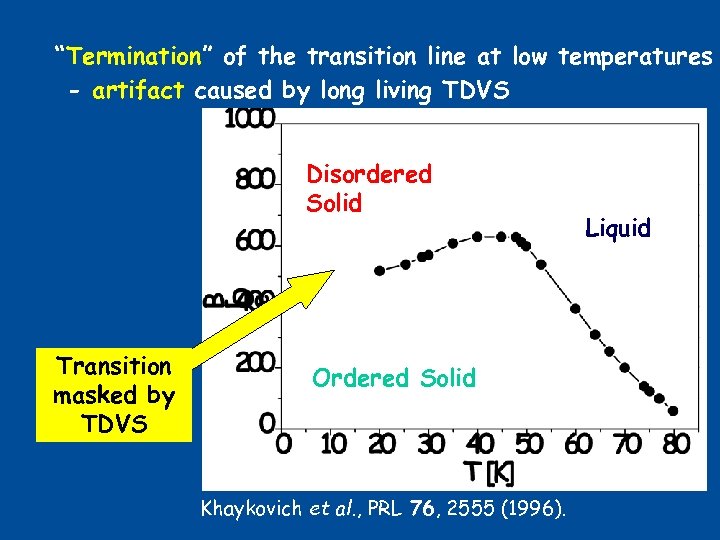“Termination” of the transition line at low temperatures - artifact caused by long living TDVS Disordered Solid ? Transition masked by TDVS Ordered Solid Khaykovich et al. , PRL 76, 2555 (1996). Liquid

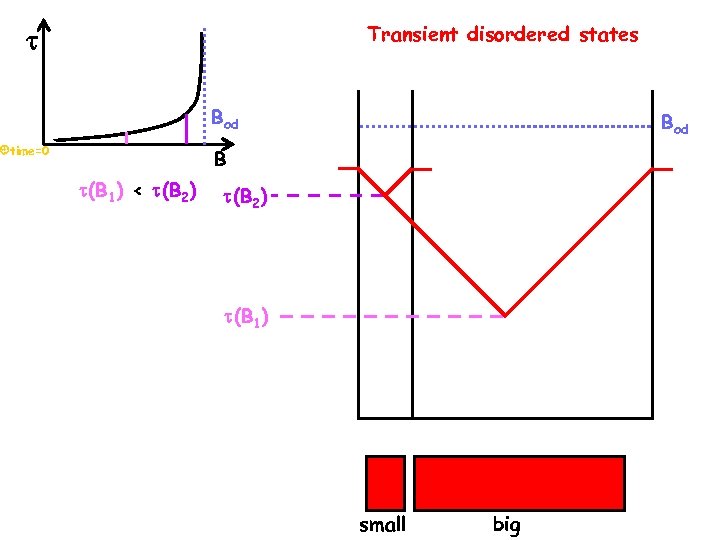Transient disordered states Bod B time=0 (B 1) < (B 2) (B 1) small big

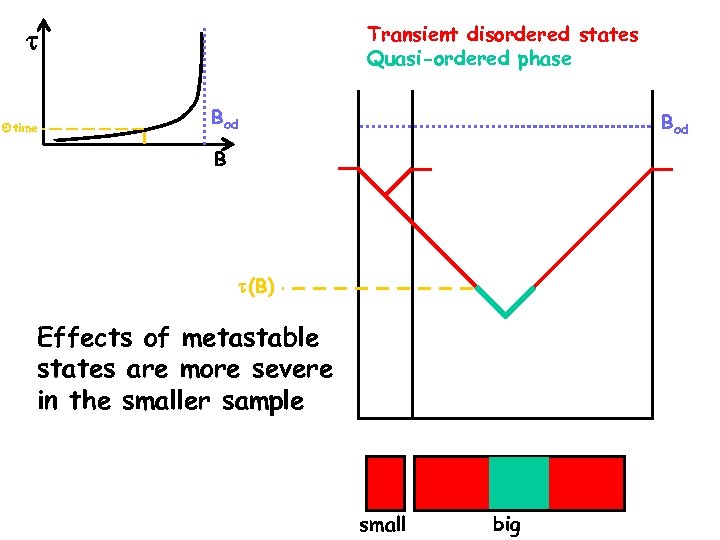Transient disordered states Quasi-ordered phase time Bod B (B) Effects of metastable states are more severe in the smaller sample Effects vortex state of states small big

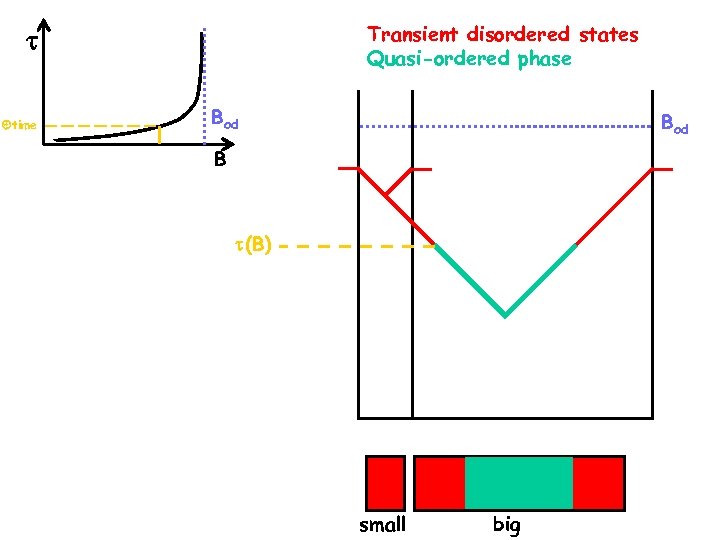Transient disordered states Quasi-ordered phase time Bod B (B) small big

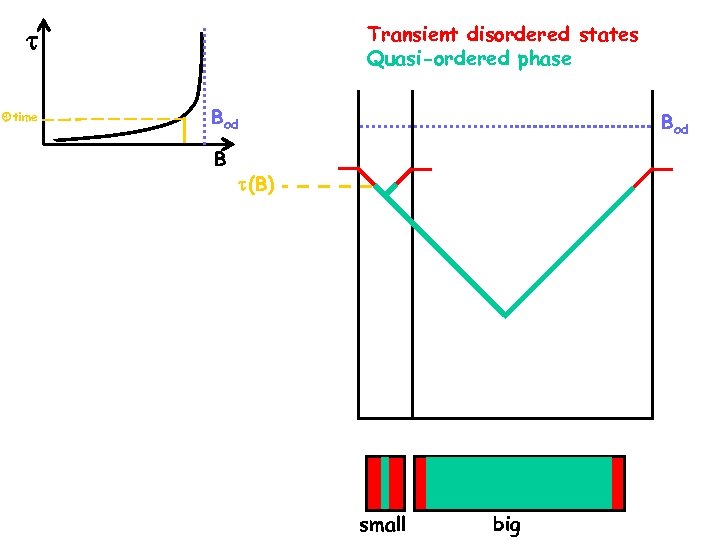Transient disordered states Quasi-ordered phase time Bod B Bod (B) small big

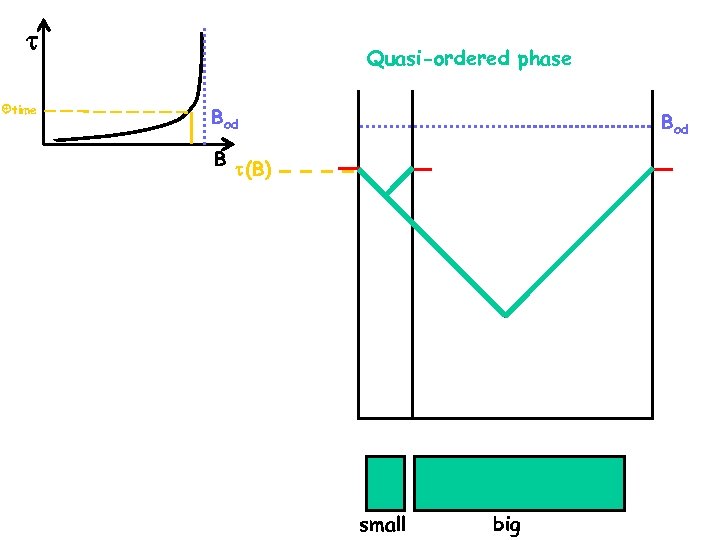time Quasi-ordered phase Bod B (B) small big

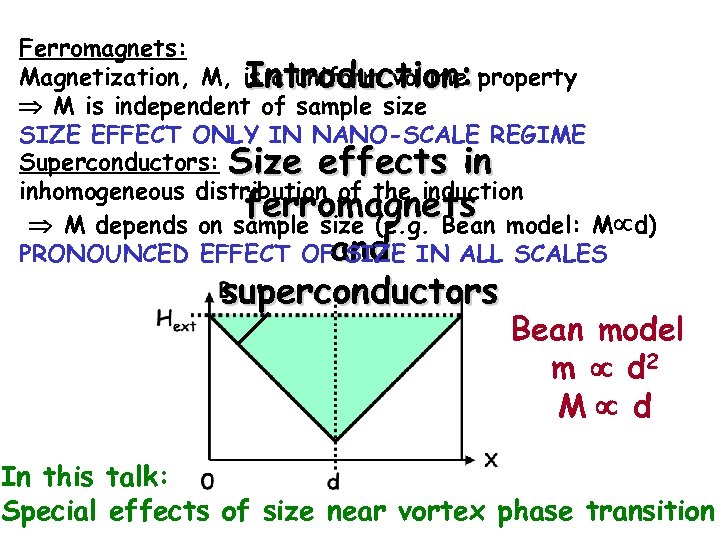Ferromagnets: Magnetization, M, is a uniform volume property Introduction: M is independent of sample size SIZE EFFECT ONLY IN NANO-SCALE REGIME Superconductors: Size effects in inhomogeneous distribution of the induction ferromagnets model: M d) M depends on sample size (e. g. Bean PRONOUNCED EFFECT OFand IN ALL SCALES SIZE superconductors Bean model m d 2 M d In this talk: Special effects of size near vortex phase transition

Summary and conclusions • Two mechanisms for the absence of the SMP: 1. Decay of persistent currents - high T 2. Involvement of metastable states - low T • Sample size plays an important role: 1. Relaxation rate 2. Relative contribution of TDVS are enhanced in smaller samples