Алгоритм АO Last.ppt
- Количество слайдов: 9

СИТЕМИ ПРОДУКЦІЙ, ЯКІ РОЗКЛАДАЮТЬСЯ 1 Якщо базу даних системи продукцій можна розкласти (Splitting) на кілька окремих баз даних, які можуть розглядатися незалежно, то таку систему називають системою продукцій, яка розкладається. Розглянемо систему продукцій з початковою базою даних БД(C, В, Z), правила продукцій якої засновані на таких правилах переписування: П 1: C (D, L); П 2: C (B, M); П 3: B (M, M); П 4: Z (B, B, M), а термінальною умовою є наявність у базі даних тільки символів М. Бачимо, що початкова база подається окремими складовими C, В і Z, які можна обробляти незалежно одну від одної. Основна процедура для системи продукцій, що розкладається: proc Split (D, R, t) Δ : = Decompose (D) M: for D∈Δ do if t (D) then Δ : = Δ {D} end if end for if Δ = ∅ then return (OK) end if D : = Select D (Δ) Δ: = Δ {D} r : = Select (D, R) if r = nil then return (fail) end if Δ : = Δ ∪ Decompose (r. f (D)) goto M end proc Це аналог процедури Production. Процедура Decompose розкладає базу даних на кілька частин (або залишає без зміни, якщо в даному стані базу розкласти неможливо). У відомому сенсі це схоже на операцію розкриття вузла. Функція Select. D аналогічна функції Select, вона фактично вибирає вузол для подальшої роботи.

І-АБО ГРАФИ 2 Для опису роботи системи продукцій у режимі декомпозиції(редукції) задачі використовують структури, що називаються І / АБО-графами і складаються з вершин, які відображають стани глобальної бази даних. Вершини-нащадки складеної бази даних, до якої було застосовано правило редукції, називають вершинами типу І, оскільки кожна з цих вершин має бути оброблена у процесі подальшої роботи системи продукцій. Вершини типу АБО отримують внаслідок застосування до Батьківської вершини правил переписування. Назва підкреслює, що Достатньо обробити будь-яку дну з вершин породжених множиною дозволених правил.

ЗАДАЧА ПРО ХАНОЙСЬКУ ВЕЖУ 3 Розглянемо підхід до розв’язання задачі методом редукції на прикладі гри “Ханойські вежі”. Є три кілки 1, 2, 3 та три диски різного розміру: А, В, С. Необхідно перекласти диски з першого кілка на третій. На кожному крокові можна перекладати тільки один диск, причому не дозволяється класти більший диск на менший. Диск більшого розміру не може розміщуватися над диском меншого розміру. Початкова та кінцева конфігурація мають, відповідно, такий вигляд: Таку задачу можна вирішити методами, які використовують простір станів. Стан гри подається вектором, координати якого вказують на кілки, де розташовані диски С (коорд. 1), В (коорд. 2) і А (коорд. 3).

РЕДУКЦІЯ ЗАДАЧІ ПРО ХАНОЙСЬКІ ВЕЖІ 4 Задачу про ханойські вежі можна розбити на три підзадачі: 1. Перекласти диск А на кілок 3; 2. Перекласти диск В на кілок 3; 3. Перекласти диск С на кілок 3. Але ці підцілі не є незалежними. Якщо одразу перекласти диск А на кілок 3, перша підціль буде досягнута. Але при цьому неможливо стане досягнути дві інші підцілі. Тому, уточнимо підцілі, розташувавши їх у порядку від найскладнішої до найпростішої: 1. Щоб перекласти всі диски на 3, потрібно перекласти туди С. При цьому на диску С не повинні знаходитись ніякі інші диски. Тобто, необхідно спочатку забезпечити можливість перекласти диск С з кілка 1 на кілок 3. 2. Перекласти диск С з кілка 1 на кілок 3. 3. Досягнути дві підцілі, які залишились (перекласти диски А і В на кілок 3). Конкретизуємо сформульовані підцілі: 1. Зняти диски А і В з кілка 1, і розташувати їх не на кілку 3, а на кілку 2. 2. Виконати переміщення диску С з кілка 1 на кілок 3. 3. Перемістити диски А і В з кілка 2 на кілок 3. Отож, остаточно подаємо задачу у вигляді трьох незалежних задач: 1. Задача про переміщення двох дисків (А і В) на кілок 2. 2. Задача про переміщення одного диску (С) на кілок 3. 3. Задача про переміщення двох дисків (А і В) на кілок 3. Кожна з цих задач є більш простішою у порівнянні з попередньою.
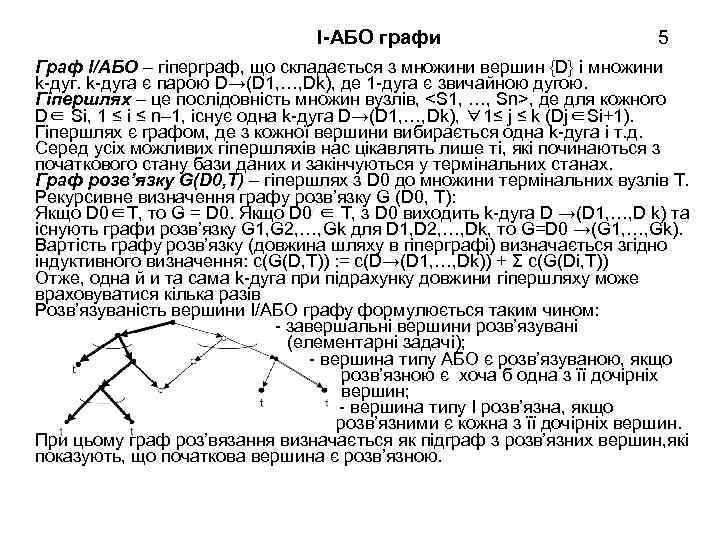
І-АБО графи 5 Граф І/АБО – гіперграф, що складається з множини вершин {D} і множини k-дуга є парою D→(D 1, …, Dk), де 1 -дуга є звичайною дугою. Гіпершлях – це послідовність множин вузлів, <S 1, …, Sn>, де для кожного D∈ Si, 1 ≤ i ≤ n– 1, існує одна k-дуга D→(D 1, …, Dk), ∀1≤ j ≤ k (Dj∈Si+1). Гіпершлях є графом, де з кожної вершини вибирається одна k-дуга і т. д. Серед усіх можливих гіпершляхів нас цікавлять лише ті, які починаються з початкового стану бази даних и закінчуються у термінальних станах. Граф розв’язку G(D 0, T) – гіпершлях з D 0 до множини термінальних вузлів T. Рекурсивне визначення графу розв’язку G (D 0, T): Якщо D 0∈T, то G = D 0. Якщо D 0 ∈ T, з D 0 виходить k-дуга D →(D 1, …, D k) та існують графи розв’язку G 1, G 2, …, Gk для D 1, D 2, …, Dk, то G=D 0 →(G 1, …, Gk). Вартість графу розв’язку (довжина шляху в гіперграфі) визначається згідно індуктивного визначення: c(G(D, T)) : = c(D→(D 1, …, Dk)) + Σ c(G(Di, T)) Отже, одна й и та сама k-дуга при підрахунку довжини гіпершляху може враховуватися кілька разів Розв’язуваність вершини І/АБО графу формулюється таким чином: - завершальні вершини розв’язувані (елементарні задачі); - вершина типу АБО є розв’язуваною, якщо розв’язною є хоча б одна з її дочірніх вершин; - вершина типу І розв’язна, якщо розв’язними є кожна з її дочірніх вершин. При цьому граф роз’вязання визначається як підграф з розв’язних вершин, які показують, що початкова вершина є розв’язною.

ПОШУК НА І-АБО ГРАФАХ (2) 6 Визначимо І/АБО графи, як гіперграфи, а дуги, які з’єднують пари вершин будемо називати гіпердугами. Гіпердуги, які з’єднують батьківську вершину з множиною дочірніх вершин будемо називати kзв’язками. Якщо всі зв’язки є 1 -зв’язками, то як окремий Випадок отримаємо звичайний граф. Розглянемо приклад І/АБО графа: Граф розв’язання, який зв’язує вершину n з множиною N термінальних(розв’язних) вершин в графі І/АБО, аналогічний шляху в звичайному графі. Але на кожному крокові створення графа розв’язання треба обирати не дугу, а зв’язку, що виходить з батьківської вершини доки кожна отримана дочірня вершина не буде належати множині N. Наприклад, для розглянутого І/АБО графа можна побудувати два різних графа розв’язання, які зв’язують вершину n 0 з множиною вершин n 7, n 8}

АЛГОРИТМ АО* ЕВРИСТИЧНОГО ПОШУКУ НА І-АБО ГРАФІ 8 Нехай є ациклічний граф, оціночна функція F, і h задовольняє умові монотонності: h(D) ≤ c(D, (D 1 , …, D k )) + Σ h(D i ) і умові спроможності: h(D) ≤ h*(D). Визначимо процедури пошуку на І-АБО графах. О – кінцеві вершини часткового графа розв’язання, Q(D) – множина дуг вузла D, x(q) – відмітка дуги

ПРОЦЕДУРА ОPEN АЛГОРИТМУ АО* 8 Процедура Оpen розкриває вибрану вершину, перераховує оцінки вершин, відмічає k-дуги и відмічає s (solved) вершини. Такі зміни можуть торкнутися усього графа. Q(D) – множина вихідних з D дуг (в G); P(D) – множина нащадків D в G; q(D) – відмічена дуга з D; x(q) – відмітка дуги; U(D) – множина предків D у G впродовж відмічених дуг; s(D) – відмітка вузла, яка означає, що з нього побудований гипершлях до цілі. Select будує фронт поточного часткового графа розв’язку по відміченим дугам и вибирає вузол з найменшою оцінкою у цьому фронті. Open розкриває вершину, перераховує оцінки вузлів, відмічає дуги і вершини. При цьому дана процедура може переоцінити увесь граф.
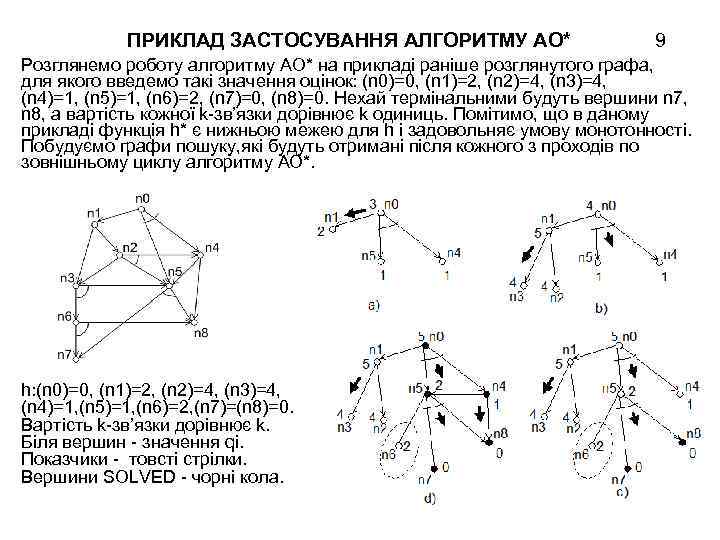
ПРИКЛАД ЗАСТОСУВАННЯ АЛГОРИТМУ АО* 9 Розглянемо роботу алгоритму АО* на прикладі раніше розглянутого графа, для якого введемо такі значення оцінок: (n 0)=0, (n 1)=2, (n 2)=4, (n 3)=4, (n 4)=1, (n 5)=1, (n 6)=2, (n 7)=0, (n 8)=0. Нехай термінальними будуть вершини n 7, n 8, а вартість кожної k-зв’язки дорівнює k одиниць. Помітимо, що в даному прикладі функція h* є нижньою межею для h і задовольняє умову монотонності. Побудуємо графи пошуку, які будуть отримані після кожного з проходів по зовнішньому циклу алгоритму АО*. h: (n 0)=0, (n 1)=2, (n 2)=4, (n 3)=4, (n 4)=1, (n 5)=1, (n 6)=2, (n 7)=(n 8)=0. Вартість k-зв’язки дорівнює k. Біля вершин - значення qi. Показчики - товсті стрілки. Вершини SOLVED - чорні кола.
Алгоритм АO Last.ppt