Системы счисления Системы счисления Непозиционная римская

Системы счисления

Системы счисления Непозиционная (римская) – XXXII Позиционная (арабская) Позиционные системы счисления двоичная (используются цифры 0, 1); восьмеричная (используются цифры 0, 1, . . . , 7); шестнадцатеричная (для чисел 0 – 9 используются цифры 0, 1, . . . , 9, для чисел 10 – 15 используются символы A, B, C, D, E, F).

1. Системы счисления: • Непозиционная (римская) – XXXII • Позиционная (арабская) - 32 «Двоичная система представляется мне прообразом творения. 1 – божественное начало, 0 – небытие. Высшее Существо создает все сущее из небытия точно так же, как математик из 1 и 0 все прочие числа» Готфрид фон Лейбниц (1646 -1716) 0 1 00 01 10 11 000 001 010 011 100 101 110 111 1 байт хранит целое число в диапазоне от 0 до 255 (от 0000 до 1111) 10–я 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2–я 0 1 10 11 100 101 110 111 1000 1001 1010 1011 1100 1101 1110 1111 10000 10001 10010 10011 8–я 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 20 21 22 23 16–я 0 1 2 3 4 5 6 7 8 9 A B C D E F 10 11 12 13

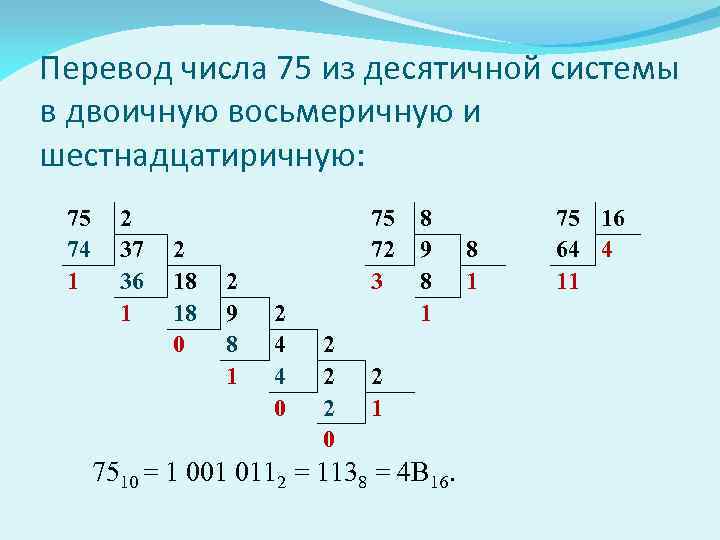Перевод числа 75 из десятичной системы в двоичную восьмеричную и шестнадцатиричную: 75 74 1 2 37 36 1 2 18 18 0 2 9 8 1 75 72 3 2 4 4 0 2 2 2 0 8 9 8 1 2 1 7510 = 1 001 0112 = 1138 = 4 B 16. 8 1 75 16 64 4 11

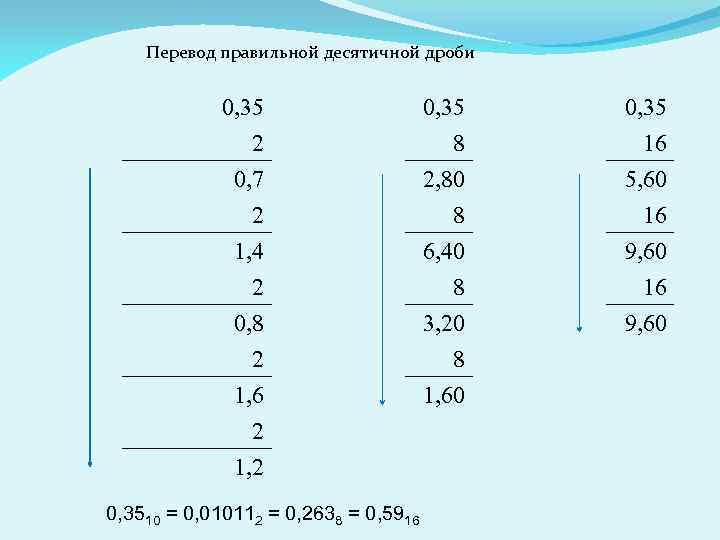Перевод правильной десятичной дроби 0, 35 2 0, 7 2 0, 35 8 2, 80 8 0, 35 16 5, 60 16 1, 4 2 0, 8 2 1, 6 2 1, 2 6, 40 8 3, 20 8 1, 60 9, 60 16 9, 60 0, 3510 = 0, 010112 = 0, 2638 = 0, 5916

Перевод из двоичной в десятичную систему счисления (an…a 3 a 2 a 1)2 = (a 1 + a 2· 2 + a 3· 22 + … + an· 2 n-1)10. Например: 11012=110 + 010· 210 + 110· 410 + 110· 810 =110+ 410 + 810 = 1310; 276, 58 = 2· 82 + 7· 81 +6· 80 + 5· 8 -1 = 190, 62510; 1 F 316 = 1· 162 + 15· 161 + 3· 160 = 49910. Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему через триады и тетрады: 537, 18 = 101 011 111, 0012 5 3 7 1 1 А 3, F 16 = 1 1010 0011, 11112 1 А 3 F

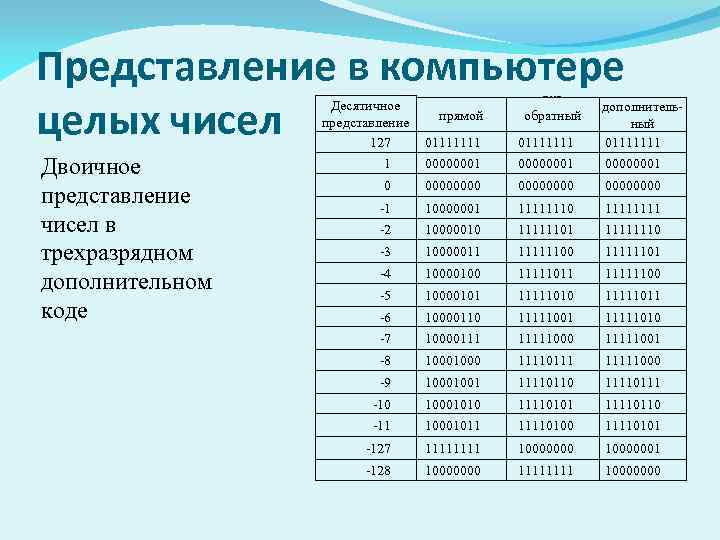Представление в компьютере целых чисел Код двоичного представления (8 бит) Двоичное представление чисел в трехразрядном дополнительном коде Десятичное дополнительпрямой обратный представление ный 127 01111111 1 00000001 0 00000000 -1 10000001 11111110 1111 -2 10000010 11111101 11111110 -3 10000011 11111100 11111101 -4 10000100 11111011 11111100 -5 10000101 11111010 11111011 -6 10000110 11111001 11111010 -7 10000111 11111000 11111001 -8 1000 11110111 11111000 -9 10001001 11110110 11110111 -10 10001010 11110101 11110110 -11 10001011 11110100 11110101 -127 1111 10000000 10000001 -128 10000000 1111 10000000

Преобразование числа из прямого кода в дополнительный Если число, записанное в прямом коде, положительное, то к нему дописывается старший (знаковый) разряд, равный 0, и на этом преобразование заканчивается; Если число, записанное в прямом коде, отрицательное, то все разряды числа инвертируются, а к результату прибавляется 1. К получившемуся числу дописывается старший (знаковый) разряд, равный 1. Пример. Преобразуем отрицательное число − 5, записанное в прямом коде, в дополнительный. Прямой код числа − 5, взятого по модулю: 101 Инвертируем все разряды числа, получая таким образом обратный код: 010 Добавим к результату 1 011 Допишем слева знаковый единичный разряд 1011 Для обратного преобразования используется тот же алгоритм. А именно: 1011 Инвертируем все разряды числа, получая таким образом обратный код : 0100 Добавим к результату 1 и проверим, сложив с дополнительным кодом 0101 + 1011 = 10000, пятый разряд выбрасывается.

Представление в компьютере дробных чисел Числа, имеющие дробную часть, также называют вещественными. В большинстве программных систем при их написании вместо запятой принято писать точку. Так, например, число 5 – целое, а числа 5. 1 и 5. 0 – вещественные. В нормальной форме число представляется в виде произведения X = m qp, где m – мантисса числа; q – основание системы счисления; p – порядок. 3, 1416 = 0, 31416 101

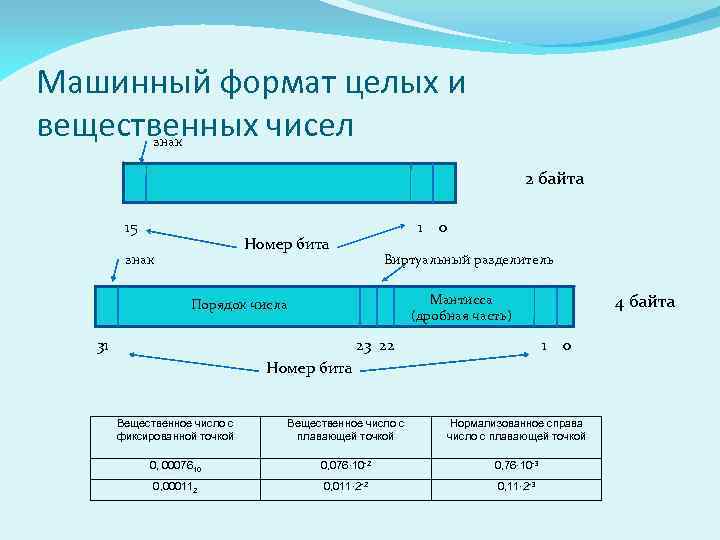Машинный формат целых и вещественных чисел знак 2 байта 15 1 0 Номер бита знак Виртуальный разделитель 4 байта Мантисса (дробная часть) Порядок числа 31 23 22 1 0 Номер бита Вещественное число с фиксированной точкой Вещественное число с плавающей точкой Нормализованное справа число с плавающей точкой 0, 0007610 0, 076· 10 -2 0, 76· 10 -3 0, 000112 0, 011· 2 -2 0, 11· 2 -3

3 Представление в компьютере текста Текстовые кодировки: ASCII - American Standart Code for Information Interchange (Американский стандартный код для обмена информацией) (ANSI) – 256 (128+128). Код каждого символа занимает 1 байт. KOI-8 (8 -разрядная кодировка) ISO 10646 (International Organisation for Standartisation – Международная организация по стандартизации) >17 млн. (32 разрядная кодировка) Unicode – 65536 (16 -разрядная кодировка) Windows-1251. Код каждого символа занимает 1 байт. H e l l o . 01001000 01100101 01101100 01101111 00101110

При кодировании (Unicode) информационный объем фразы Ученье – свет, а неученье – тьма. составляет …

5 Представление в компьютере звука Дискретизация (оцифровка) звука MIDI MP 3

Кодирование звуковой информации Можно выделить два основных направления: Метод FM – основан на том, что любой сложный звук можно разложить на последовательность простейших гармонических сигналов разных частот; Метод таблично-волнового синтеза. В заранее подготовленных таблицах хранятся образцы звуков для множества различных музыкальных инструментов (сэмплы).