Системы счисления представление чисел в компьютере Часть

Системы счисления, представление чисел в компьютере

Часть 1 Системы счисления

Эволюция систем счисления • Вавилонская – 60 -ричная (осталась для обозначения времени и углов) • Греческая – непозиционная, • Римская – непозиционная, I II IV V VI VIII IX X XI L C M • Двенадцатеричная – дюжина, гросс, масса; 1 фут=12 дюймов, 1 шиллинг = 12 пенсов • Прочие – 2 (Австралия, Полинезия), 5 (Африка), 20 (Кельты, Майя, Ацтеки) • Индийская, арабская – позиционная, десятичная

Какие бывают системы счисления? • Непозиционные • Позиционные Значение цифры зависит от ее положения в числе ak*pk + ak-1*pk-1 + … + a 1*p 1 + a 0*p 0 • Однородные • Смешанные Более одного основания

Какие системы используются в ЭВМ? Аппаратура • Двоичная Программное обеспечение • Двоичная • Восьмеричная • Шестнадцатеричная

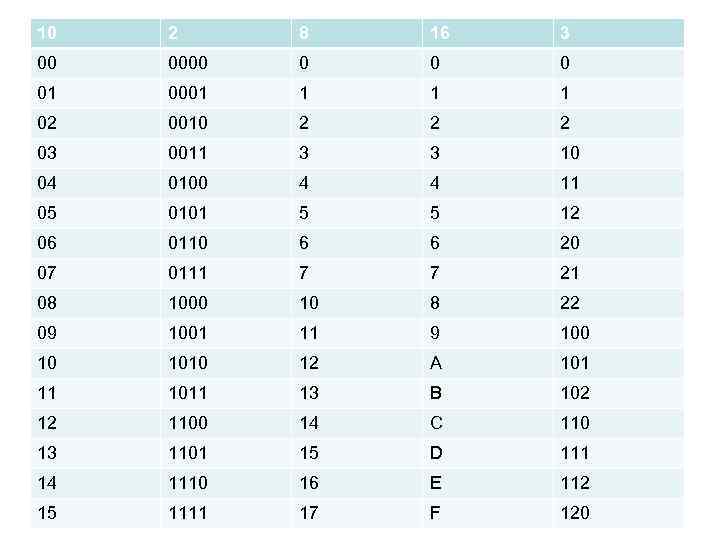10 2 8 16 3 00 0000 0 01 0001 1 02 0010 2 2 2 03 0011 3 3 10 04 0100 4 4 11 05 0101 5 5 12 06 0110 6 6 20 07 0111 7 7 21 08 1000 10 8 22 09 1001 11 9 100 10 1010 12 A 101 11 1011 13 B 102 12 1100 14 C 110 13 1101 15 D 111 14 1110 16 E 112 15 1111 17 F 120

Двоичная система счисления Если , где то xd - запись числа x в d-ичной системе счисления содержит m+n+1 цифр. Целая часть содержит m+1 цифр, дробная n. Пример: 10910 = 1 * 102 + 0 * 101 + 9 * 100 = 109 11011012 = 1 * 26 + 1 * 25 + 0 * 24 + 1 * 23 + 1 * 22 + 0 * 21 + 1 * 20 = = 64 + 32 + 8 + 4 + 1 = 109 3. 1562510 = 3 * 100 + 1 * 10 -1 + 5 * 10 -2 + 6 * 10 -3 + 2 * 10 -4 + 5 * 10 -5 = = 3. 15625 11. 001012 = 1 * 21 + 1 * 20 + 0 * 2 -1 + 0 * 2 -2 + 1 * 2 -3 + 0 * 2 -4 + 1 * 2 -5 = = 2 + 1/8 + 1/32 = 3. 15625

Двоичная система счисления перевод из двоичной системы счисления в десятичную 1. представление числа в виде суммы степеней двоек 2. вычисление суммы 1001. 01012= = 1*23 + 0*22 + 0*21 + 1*20 + + 0*2 -1 + 1*2 -2 + 0*2 -3 + 1*2 -4 = = 8 + 0 + 1/4 + 0 + 1/8 = 9. 37510

Двоичная система счисления перевод из десятичной системы счисления в двоичную 13410 134. 6562510 Последовательно делим число на 2, сохраняем на каждой итерации остатки от деления на 2. Продолжаем пока число не равно 0. 1 а. Остаток от деления 134 на 2 равен 0, т. е. 134 % 2 = 0 1 b. 134 / 2 = 67 2 а. 67 % 2 = 1 2 b. 67 / 2 = 33 (целочисленное деление!) 3. 33 % 2 = 1, 33 / 2 = 16 4. 16 % 2 = 0, 16 / 2 = 8 5. 8 % 2 = 0, 8 / 2 = 4 6. 4 % 2 = 0, 4 / 2 = 2 7. 2 % 2 = 0, 2 / 2 = 1 8. 1 % 2 = 1, 1 / 2 = 0 Объединяем остатки в обратном порядке: 13410 = 100001102 0. 6562510 Последовательно сравниваем число с 1/2, если число меньше 1/2, то запоминает 0 и удваиваем, иначе запоминает 1, отнимает 1/2 и удваиваем. Продолжаем, пока не получим 0. 1. 0. 65625 >= 1/2, запоминаем 1, 2*(0. 65625 - 1/2) = 0. 3125 2. 0. 3125 < 1/2, запоминаем 0, 2*0. 3125 = 0. 625 3. 0. 625 >= 1/2, запоминаем 1, 2*(0. 625 – 1/2) = 0. 25 4. 0. 25 < 1/2, запоминаем 0, 2*(0. 25 – 1/2) = 0. 5 5. 0. 5 >= 1/2, запоминаем 1, 2*(0. 5 – 1/2) = 0. 0 Объединяем запомненные цифры в прямом порядке 0. 6562510 = 101012 10000110. 101012

Двоичная система счисления перевод из десятичной системы счисления в двоичную Десятичная дробь 0. 2 в двоичном представлении бесконечна и периодична. 1. 0. 2 < 1/2, запоминаем 0 2*0. 2 = 0. 4 2. 0. 4 < 1/2, запоминаем 0 2*0. 4 = 0. 8 3. 0. 8 >= 1/2, запоминаем 1 2*(0. 8 -1/2) = 0. 6 4. 0. 6 >= 1/2, запоминаем 1 2*(0. 6 -1/2) = 0. 2 … Таким образом, 0. 210 = 0. 00110011… = 0. (0011)2

Часть 2 Представление чисел в компьютере

Представление беззнаковых целых чисел Для представления беззнакового (т. е. неотрицательного) целого числа его необходимо перевести в двоичное представление и записать полученную последовательность 0 и 1 (битов) в соответствующие ячейки памяти. Например, 12310 = 11110112 Поэтому представление числа 123 с помощью однобайтового типа данных (unsigned char в C) будет следующим: 0 7 0 1 1 Однобайтовый тип данных позволяет представлять числа от 0 до 28 -1: 0 0 0 0 0 1 1 1 28 -1 = 255 1 1

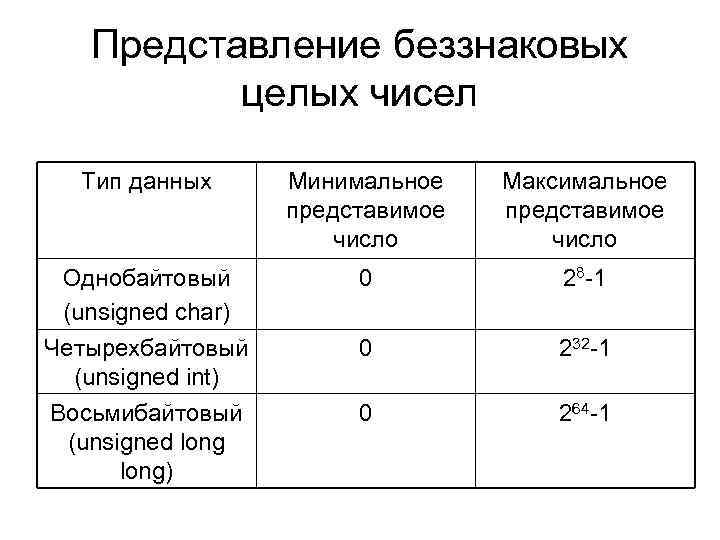Представление беззнаковых целых чисел Тип данных Минимальное представимое число Максимальное представимое число Однобайтовый (unsigned char) Четырехбайтовый (unsigned int) 0 28 -1 0 232 -1 Восьмибайтовый (unsigned long) 0 264 -1

Ошибочные ситуации при целочисленной арифметике • Переполнение, недополнение – чтение и установка флага переноса в арифметических командах, – операции с насыщением, – произвольная точность • Деление на нуль – обработка исключительной ситуации

Представление знаковых целых чисел Знаковые целые числа в памяти компьютера представляются с помощью дополнительного кода. Вычисление дополнительного кода числа x: 1. Если x ≥ 0, то дополнительный код x совпадает с его двоичным представлением 2. Если x < 0, то для получение дополнительного кода необходимо: А. найди двоичное представление модуля x B. Изменить все биты в двоичном представлении x на противоположные С. Прибавить единицу Например, представим число -84 в знаковом однобайтовом типе (тип char в C): А. |-8410| = 8410 = 26 + 24 + 22 = 010101002 B. Инвертируем все биты: 010101002 → 101010112 С. Прибавляем единицу: 101010112 + 12 = 101011002 0 7 1 0 1 1 0 0

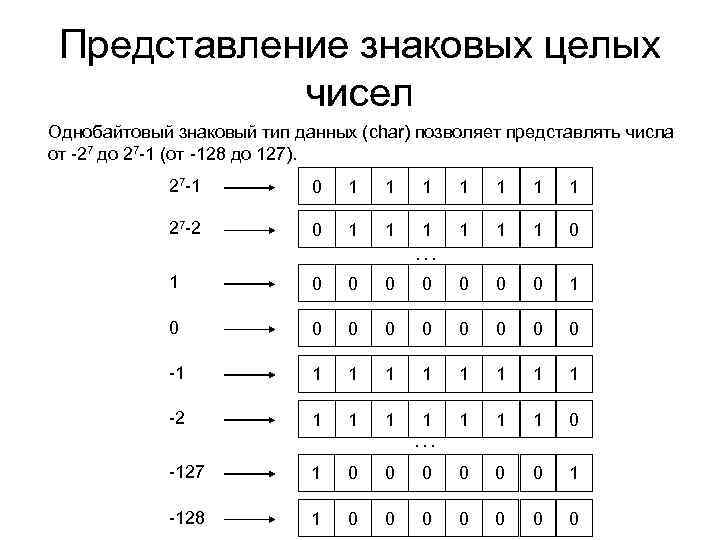Представление знаковых целых чисел Однобайтовый знаковый тип данных (char) позволяет представлять числа от -27 до 27 -1 (от -128 до 127). 27 -1 0 1 1 1 1 27 -2 0 1 1 1 0 1 0 0 0 0 0 -1 1 1 1 1 -2 1 1 1 1 0 -127 1 0 0 0 1 -128 1 0 0 0 0 … …

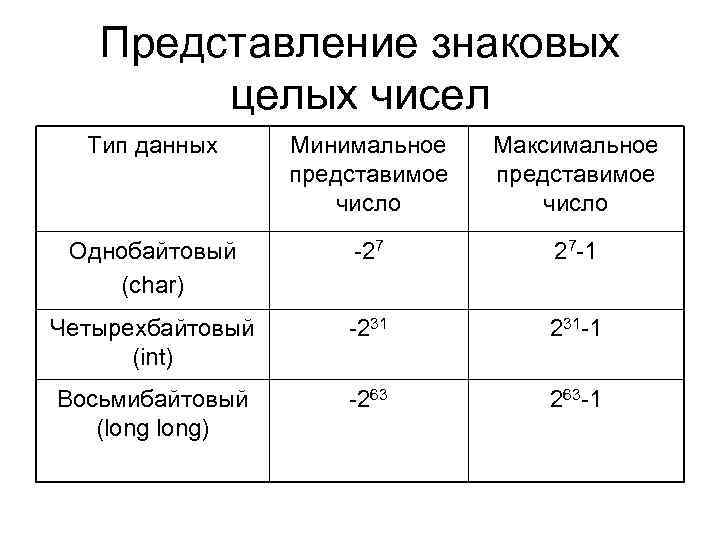Представление знаковых целых чисел Тип данных Минимальное представимое число Максимальное представимое число Однобайтовый (char) -27 27 -1 Четырехбайтовый (int) -231 231 -1 Восьмибайтовый (long) -263 263 -1

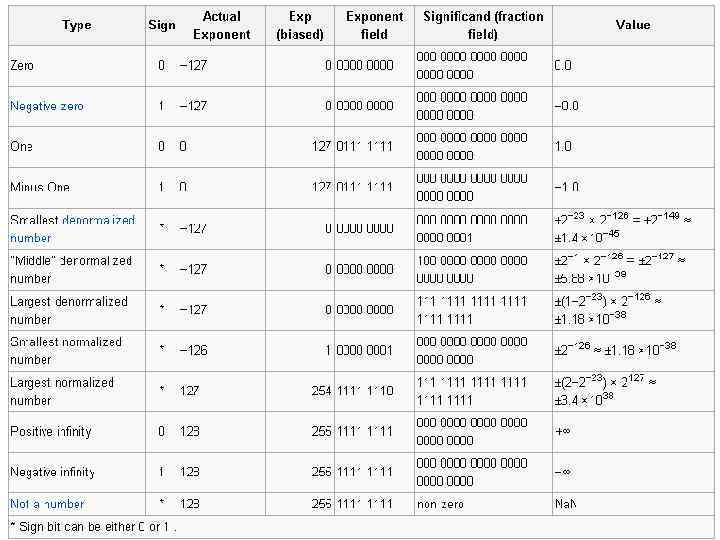
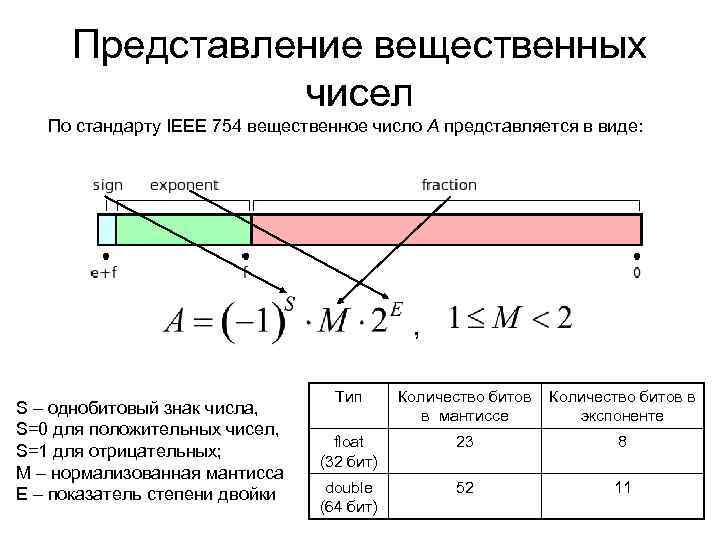Представление вещественных чисел По стандарту IEEE 754 вещественное число А представляется в виде: , S – однобитовый знак числа, S=0 для положительных чисел, S=1 для отрицательных; M – нормализованная мантисса E – показатель степени двойки Тип Количество битов в мантиссе Количество битов в экспоненте float (32 бит) 23 8 double (64 бит) 52 11

Представление вещественных чисел Пример представления числа (0. 15625)10=(0. 00101)2 в типе float. Необходимо представить число в виде произведения где. 0. 15625 = 1. 25 · 2 -3, таким образом, S = 0, M = 1. 2510, E = -310. 15625 > 0, поэтому sign = 0. 2. Вычислим двоичное представление мантиссы M = 1. 2510 = 1. 012. В силу условия нормализованности мантиссы (1 ≤ M < 2) мантисса всегда начинается в единицы, что позволяет записывать только дробную ее часть. Поэтому fraction = 012. 3. Показатель степени вычисляется следующим образом: exponent = E + (2 q-1 – 1)10, где q – количество битов, выделяемых под порядок (в случае float q=8). Таким образом, exponent = -310 + (28 -1 – 1)10 = -310 + 12710 = 12410 = 11111002 В результате, число 0. 15625 представимо в следующем виде: sign exponent (8 битов) fraction (23 бита) 0011111000000000000 23 31 0

Представление вещественных чисел Для стандартных типов данных имеет место следующие значения: Тип Минимальный десятичный порядок Максимальный десятичный порядок Число значащих десятичных знаков float -45* 38 7 double -323 308 15 * Стоит отметить, что мантисса может быть ненормализованной, что и приводит к таким значениям минимального порядка. Под мантиссу в float отводится 23 бита + 1 неявный, т. о. , получается 24 значащих двоичных знака или 7 десятичных знаков в силу того, что 224 ≈ 107. Максимальный двоичный порядок 27 -1, поэтому максимальный десятичный порядок равен 38, т. к. 2^(27 -1) ≈ 1038.