СИСТЕМЫ СЧИСЛЕНИЯ План Лекции Понятие системы счисления (СС)

СИСТЕМЫ СЧИСЛЕНИЯ План Лекции Понятие системы счисления (СС) Непозиционные СС (НПСС), примеры НПСС Позиционные СС (ПСС) - представление чисел с основанием 10, 2, 8, 16 и с произвольным основанием - перевод чисел из ПСС с одним основанием в ПСС с другим основанием - арифметические операции в неограниченной и ограниченной разрядной сетке, перенос и переполнение - знаковые и беззнаковые числа

2 Понятие Системы Счисления Система счисления – это способ представления чисел и правила действий над ними. Цифры – это знаки, используемые при записи чисел в данной CС. Алфавит – это полный набор символов данной СС (цифры, разделители целой и дробной части, «-») римская СС: I, V, X,… двоичная СС: 0, 1 десятичная СС: 0, 1, 2, …9

3 Непозиционные Системы Счисления Непозиционная система счисления – это СС, в которой значение каждой цифры не зависит от ее положения (места, позиции) в записи числа. Римская СС для обозначения цифр использует буквы римского алфавита: Например: CCCXXVII = 327 Цифра C независимо от того, где она находится, обозначает только свой количественный эквивалент 100. То же самое касается цифр X и I.

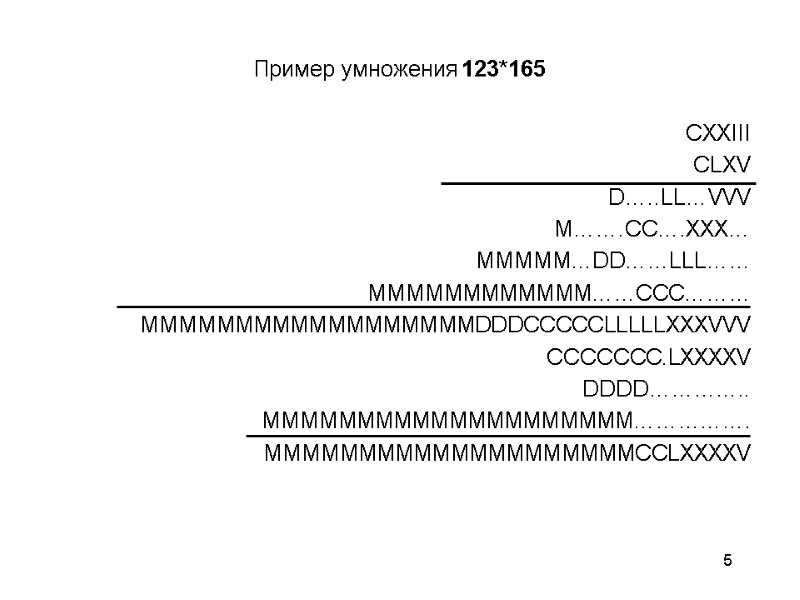
4 Используются следующие правила: В числе цифры записываются слева направо в порядке убывания. Величина числа определяется как сумма или разность цифр в числе. Если меньшая цифра стоит слева от большей цифры, то она вычитается, если справа – прибавляется: MDCLXVI = 1000+500+100+50+10+5+1=1666 MCDXLIV = 1000-100+500-10+50-1+5=1444 Запрещена запись буквы I в цифре более трех раз подряд XIX – верная запись, XVIIII – не верная запись.

5

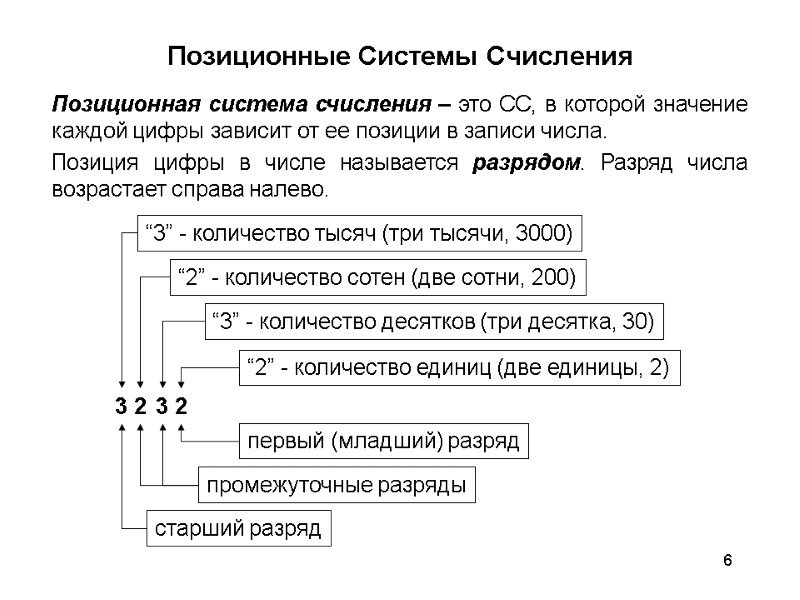
6 Позиционные Системы Счисления Позиционная система счисления – это СС, в которой значение каждой цифры зависит от ее позиции в записи числа. Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево.

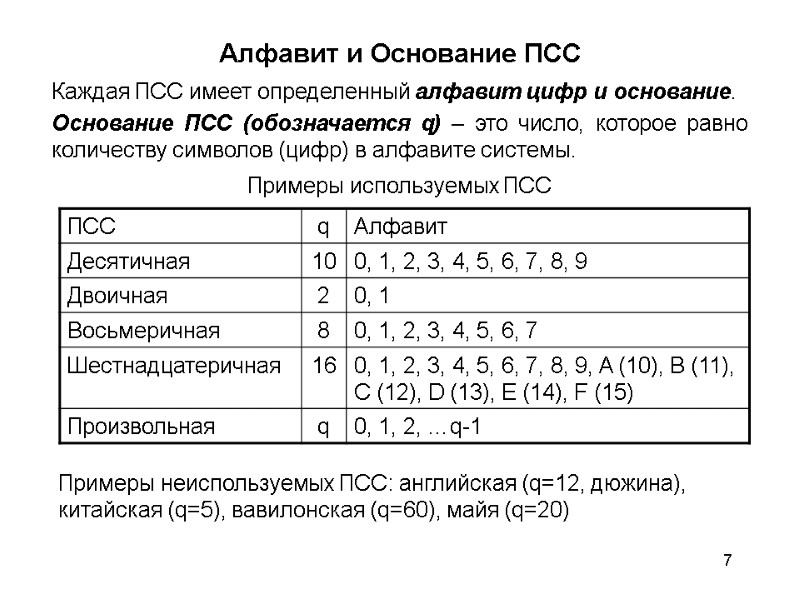
7 Алфавит и Основание ПСС Примеры используемых ПСС Каждая ПСС имеет определенный алфавит цифр и основание. Основание ПСС (обозначается q) – это число, которое равно количеству символов (цифр) в алфавите системы. Примеры неиспользуемых ПСС: английская (q=12, дюжина), китайская (q=5), вавилонская (q=60), майя (q=20)

8 Запись Числа в Свернутой и Развернутой Форме Свернутая запись : Здесь: Aq – само число, q – основание СС, аi – цифры данной СС, n – число разрядов целой части числа, m - число разрядов дробной части числа. Развернутая запись :

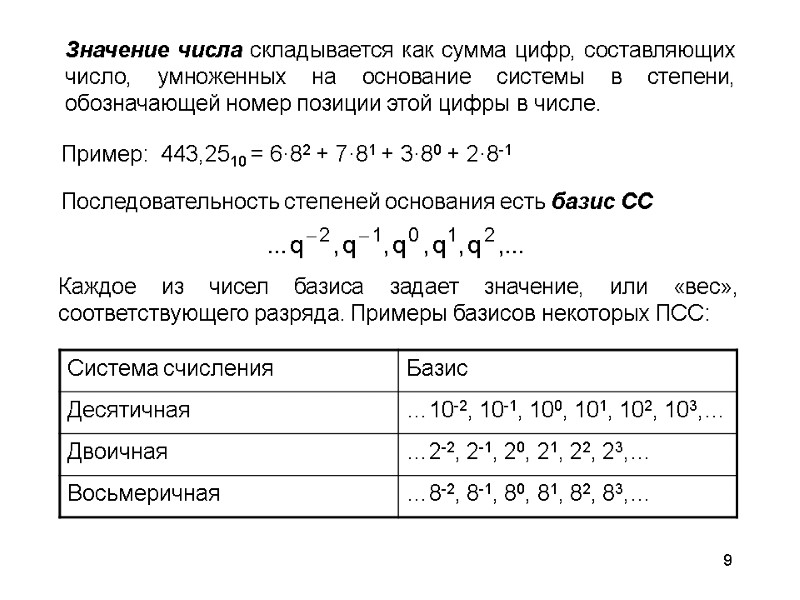
9 Значение числа складывается как сумма цифр, составляющих число, умноженных на основание системы в степени, обозначающей номер позиции этой цифры в числе. Последовательность степеней основания есть базис СС Каждое из чисел базиса задает значение, или «вес», соответствующего разряда. Примеры базисов некоторых ПСС: Пример: 443,2510 = 6·82 + 7·81 + 3·80 + 2·8-1

10 В математике существует термин: разложить по базису. Применительно к представлению чисел в разных ПСС это значит представить число в развернутой форме. Из формулы для представления числа в развернутом виде следует общий для всех ПСС вывод: умножение или деление числа на основание СС приводит к сдвигу запятой, отделяющей целую и дробную части, вправо или влево соответственно: 333,3310·10 = 3333,310 101,012·2 = 1010,12 333,3310:10 = 33,33310 101,012:2 = 10,1012 Примеры: разложить по базису системы счисления числа 101,01; 673,28; 15FC16 Решение: 101,01 = 1·22 + 0·21 + 1·20 + 0·2-1 +1·2-2 673,28 = 6·82 + 7·81 + 3·80 + 2·8-1 15FC16 = 1·163 + 5·162 + F·161 + C·160

11 Для перевода числа в десятичную СС из любой ПСС (с произвольным основанием) необходимо записать это число в развернутой форме и вычислить его значение: Перевод Чисел из ПСС с Одним Основанием в ПСС с Другим Основанием Пример 1. Перевод из двоичной системы: 10,112 = 1·21 + 0·20 + 1·2-1 +1·2-2 = 1·2 + 0·1 + 1·1/2 +1·1/4 = 2,7510 Пример 2. Перевод из восьмеричной системы: 67,58 = 6·81 + 7·80 + 5·8-1 = 6·8 + 7·1 + 5·1/8 = 55,62510 Пример 3. Перевод из шестнадцатеричной системы: 19F16 = 1·162 + 9·161 + F·160 = 1·256 + 9·16 + 15·1 = 41510

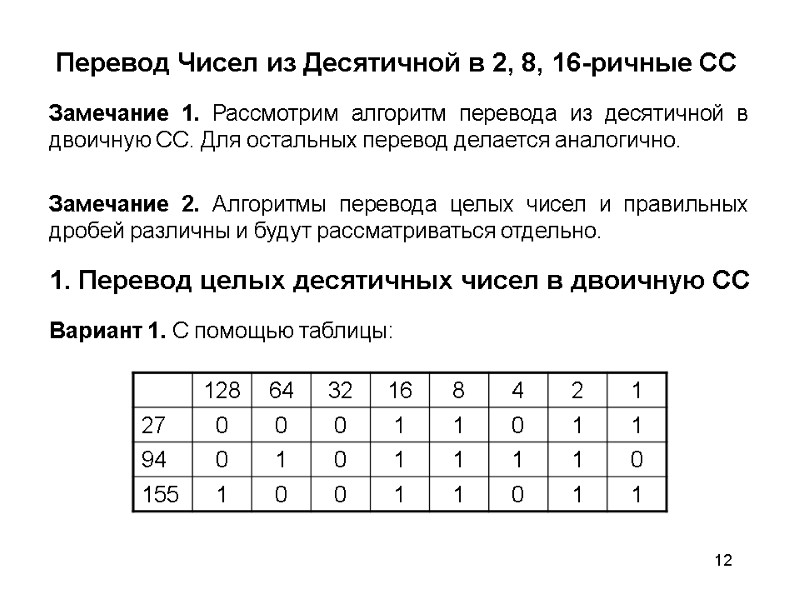
12 Перевод Чисел из Десятичной в 2, 8, 16-ричные СС Замечание 1. Рассмотрим алгоритм перевода из десятичной в двоичную СС. Для остальных перевод делается аналогично. Замечание 2. Алгоритмы перевода целых чисел и правильных дробей различны и будут рассматриваться отдельно. 1. Перевод целых десятичных чисел в двоичную СС Вариант 1. С помощью таблицы:

13 Вариант 2. Любое целое десятичное число А10 может быть разложено по базису степеней основания q=2: Разделим А10 на 2. Частное будет равно: а остаток будет равен а0. Продолжая этот процесс, после n-ого шага получим последовательность остатков: совпадающую с обратной последовательностью цифр целого двоичного числа, записанного в свернутой форме:

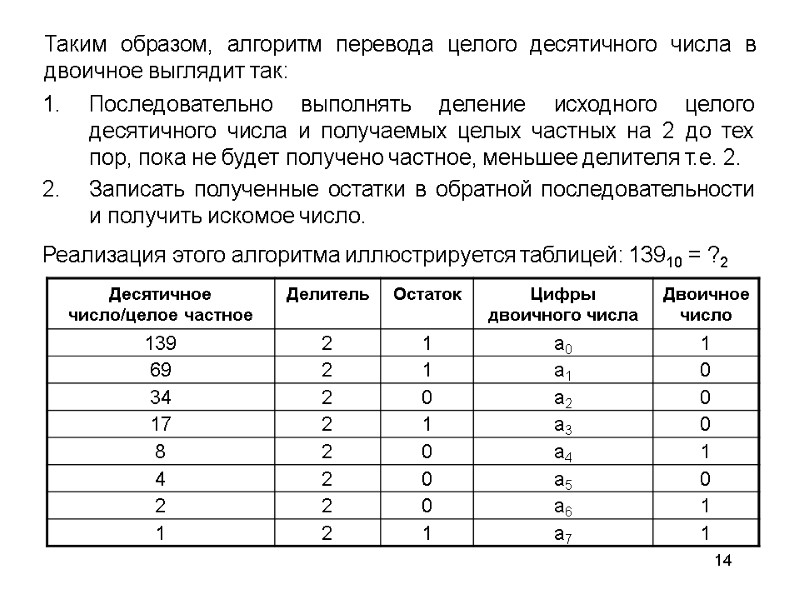
14 Последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных на 2 до тех пор, пока не будет получено частное, меньшее делителя т.е. 2. Записать полученные остатки в обратной последовательности и получить искомое число. Таким образом, алгоритм перевода целого десятичного числа в двоичное выглядит так: Реализация этого алгоритма иллюстрируется таблицей: 13910 = ?2

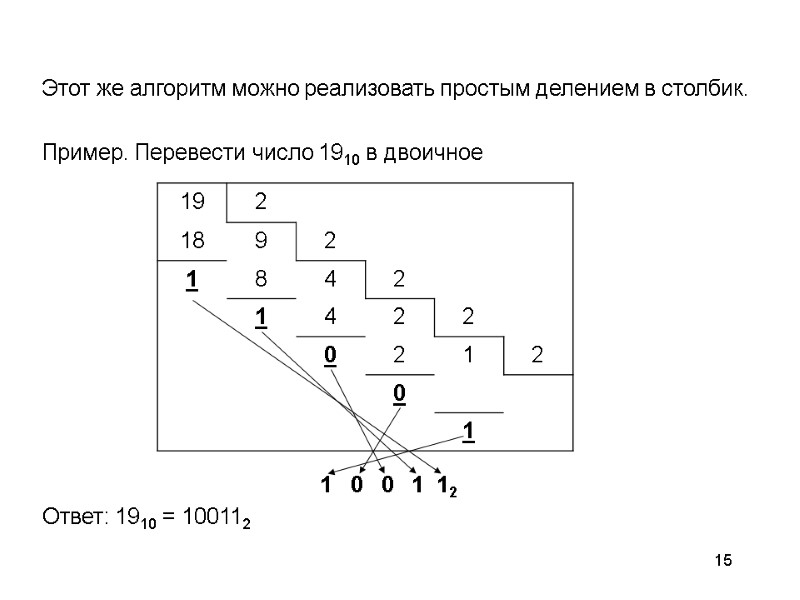
15 Этот же алгоритм можно реализовать простым делением в столбик. Пример. Перевести число 1910 в двоичное Ответ: 1910 = 100112 1 0 0 1 12

16 2. Перевод десятичных дробей в двоичную СС Любая десятичная дробь А10 может быть разложено по базису степеней основания q=2: Умножим А10 на 2. Произведение будет равно: Целая часть равна а-1. Продолжая этот процесс до тех пор, пока не будет получена дробная часть, равная 0, или не будет достигнута требуемая точность вычислений. Найденная при этом последовательность цифр совпадает с последовательностью цифр дробного двоичного числа:

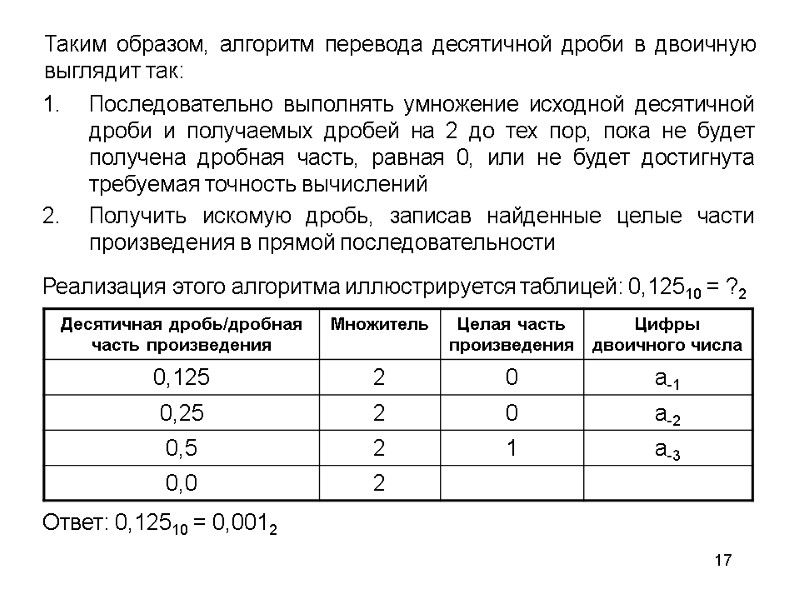
17 Последовательно выполнять умножение исходной десятичной дроби и получаемых дробей на 2 до тех пор, пока не будет получена дробная часть, равная 0, или не будет достигнута требуемая точность вычислений Получить искомую дробь, записав найденные целые части произведения в прямой последовательности Таким образом, алгоритм перевода десятичной дроби в двоичную выглядит так: Реализация этого алгоритма иллюстрируется таблицей: 0,12510 = ?2 Ответ: 0,12510 = 0,0012

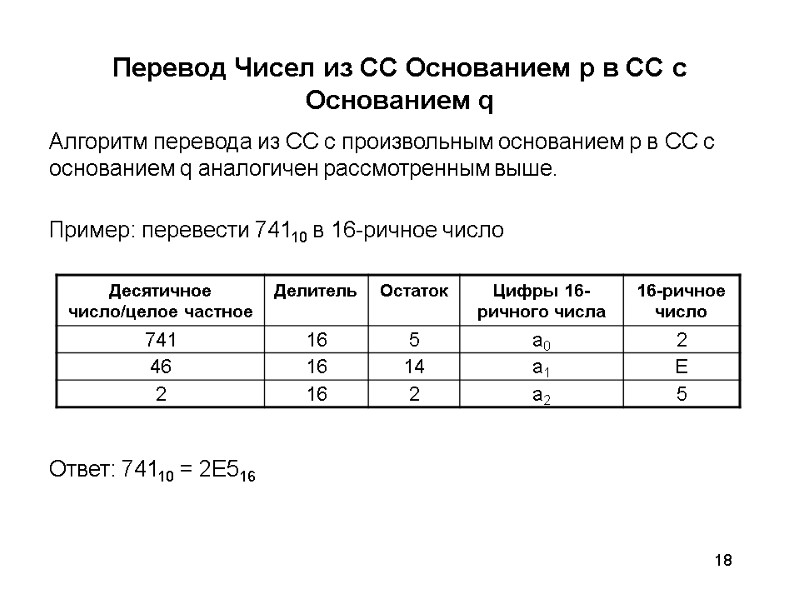
18 Перевод Чисел из СС Основанием p в СС с Основанием q Алгоритм перевода из СС с произвольным основанием p в СС с основанием q аналогичен рассмотренным выше. Пример: перевести 74110 в 16-ричное число Ответ: 74110 = 2Е516

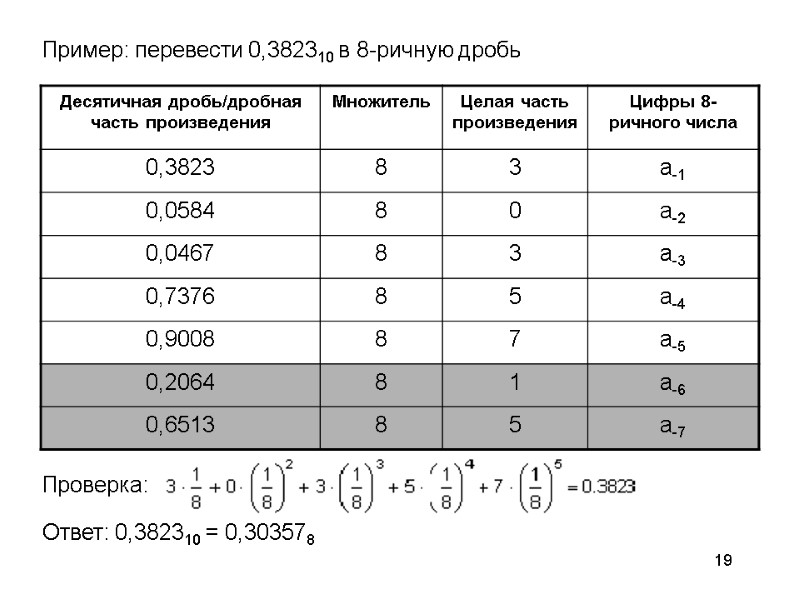
19 Пример: перевести 0,382310 в 8-ричную дробь Проверка: Ответ: 0,382310 = 0,303578

20 Перевод Чисел из Двоичной СС в 8 и 16-ричные и Обратно Алгоритм перевода из двоичной СС в 8 и 16-ричные СС и обратно проще описанного выше. Вспомним, что каждый разряд двоичного числа содержит 1 бит, каждый разряд 8-ричного числа содержит 3 бит, каждый разряд 16-ричного числа содержит 4 бит. Следовательно, для перевода целой части двоичного числа:

21 Вспомогательные Таблицы Пример: 1010012  101 001  518 1010012  0010 1001  2916 Для перевода двоичных чисел в 8-ричные Для перевода двоичных чисел в 16-ричные

22 Для перевода дробного двоичного числа:

23 Алгоритм перевода из 8 и 16-ричных СС в двоичную Для перевода чисел из 8 и 16-ричных СС в двоичную необходимо цифры числа преобразовать в группы двоичных чисел. При переводе из 8-ричной СС каждую цифру восьмеричного числа нужно преобразовать в триаду – группу из трех двоичных разрядов Пример: 748 7  111, 4  100 Ответ: 748 = 1111002 При переводе из 16-ричной СС каждую цифру шестнадцатеричного числа нужно преобразовать в тетраду – группу из четырех двоичных разрядов Пример: 0,BA16 B  1011, A  1010 Ответ: 0,BA16 = 0,101110102

24 Арифметические Операции в Неограниченной Разрядной Сетке Сложение (на примере двоичной системы). Таблица сложения одноразрядных двоичных чисел 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10 Если значение числа в некотором разряде становится равным или большим основания – происходит переполнение. При этом производится перенос единицы в старший разряд.

25 Вычитание (на примере двоичной системы). Таблица вычитания одноразрядных двоичных чисел В таблиц чертой над 1 обозначен заем из старшего разряда Если уменьшаемое по абсолютной величине больше вычитаемого, то вычитание происходит аналогично десятичной СС

26 Если уменьшаемое по абсолютной величине меньше вычитаемого, то результат получается в так называемом дополнительном коде В памяти отрицательные числа хранятся сразу в дополнительном коде. Чтобы преобразовать число в дополнительный код нужно: 1. Перевести его в обратный код (т.е. поменять 1 на 0 и наоборот) 2. Прибавить 1. Пример: 01010011 (прямой)  10101100 (обр.)  10101101 (доп.)