Системы счисления Перевод из одной системы счисления в

Системы счисления. Перевод из одной системы счисления в другую.

Система счисления (СС) - это способ изображения чисел и соответствующие ему правила действия над числами. Непозиционные системы счисления – в таких системах счисления от положения знака в записи числа не зависит величина, которую он обозначает. Пример непозиционной СС (римская система): I , V, X, L, C, D, M 1, 5, 10, 50, 100, 500, 1000 Позиционные системы: • В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции. • Количество используемых цифр называется основанием позиционной системы счисления.

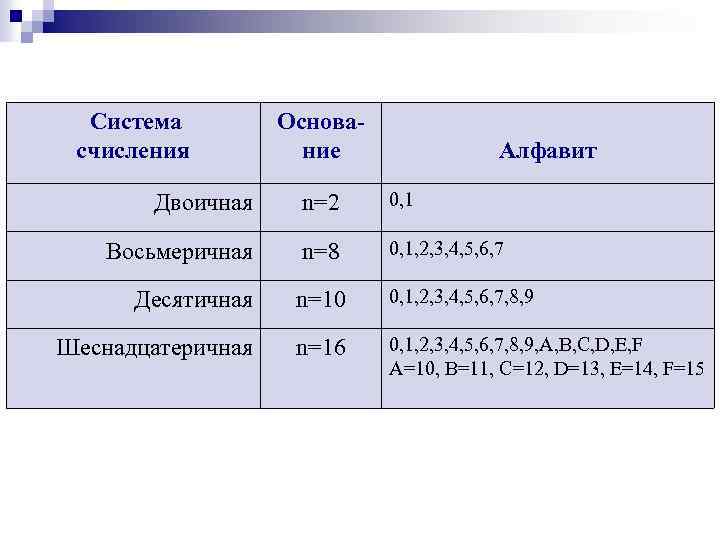Система счисления Основание Алфавит Двоичная n=2 0, 1 Восьмеричная n=8 0, 1, 2, 3, 4, 5, 6, 7 Десятичная n=10 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Шеснадцатеричная n=16 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F A=10, B=11, C=12, D=13, E=14, F=15

I. Перевод из 10 -ой системы в любую другую позиционную систему счисления: Перевод целых десятичных чисел в любую другую позиционную систему счисления осуществляется последовательным делением десятичного числа на основание той системы, в которую оно переводится, до тех пор, пока не получится частное меньшее этого основания. Число в новой системе записывается в виде остатков деления, начиная с последнего.

II. Перевод чисел из любой системы счисления в 10 -ую систему: В позиционной системе счисления число можно разложить по степеням основания: 2 1 0 -1 -2 С этим правилом связан способ перевода чисел из любой системы счисления в 10 -ую систему:

III. Перевод чисел из 8 -oй, 16 -ой систем счисления в 2 -ую систему и обратно : Основание n =2 Таблица соответствия двоичных триад цифрам 8 -ой системы счисления 0 1 010 2 011 3 100 Одной восьмеричной цифре соответствует 3 двоичных цифры. Тройка двоичных цифр называется триадой. 000 001 2³=8 Основание n =8 4 101 5 110 6 111 7

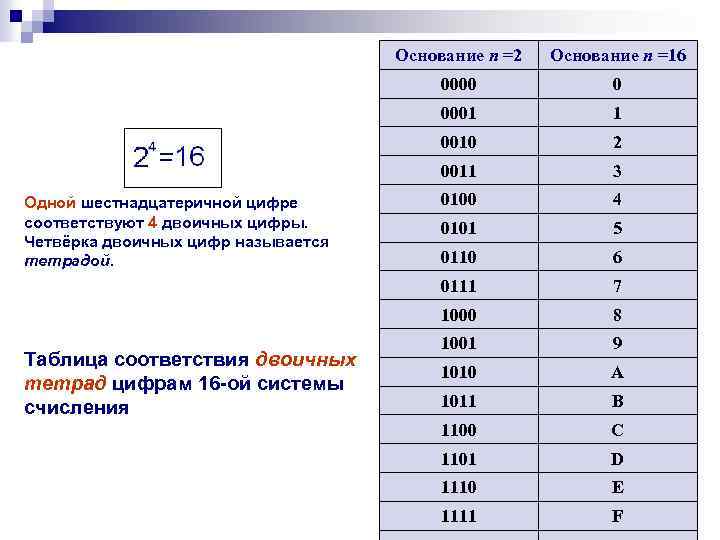Основание n =2 0000 1 0010 2 0011 3 0100 4 0101 5 0110 6 0111 7 1000 Таблица соответствия двоичных тетрад цифрам 16 -ой системы счисления 0 0001 Одной шестнадцатеричной цифре соответствуют 4 двоичных цифры. Четвёрка двоичных цифр называется тетрадой. Основание n =16 8 1001 9 1010 A 1011 B 1100 C 1101 D 1110 E 1111 F

Для перевода восьмеричного или шестнадцатеричного числа в двоичную форму достаточно заменить каждую цифру этого числа соответствующим трехразрядным двоичным числом (триадой) или четырехразрядным двоичным числом (тетрадой), при этом отбрасывают ненужные нули в старших и младших разрядах. Пример. 2 0 1 1 0 0 0 1 1 0 0 2 0 1 1 1 1 0 1 1 0 0 1 0 1 1 1 0

Для перехода от двоичной к восьмеричной (шестнадцатеричной) системе поступают следующим образом: двигаясь от точки влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем триаду (тетраду) заменяют соответствующей восьмеричной (шестнадцатеричной) цифрой. Пример. 2 2

IV. Перевод из восьмеричной в шестнадцатеричную систему и обратно осуществляется через двоичную систему с помощью триад и тетрад. Пример: 8 8 2 16 8 16 2

V. Перевод правильных дробей из десятичной системы счисления: Для перевода правильной десятичной дроби в другую систему эту дробь надо последовательно умножать на основание той системы, в которую она переводится. При этом умножаются только дробные части. Дробь в новой системе записывается в виде целых частей произведений, начиная с первого. Пример. 10 10 8

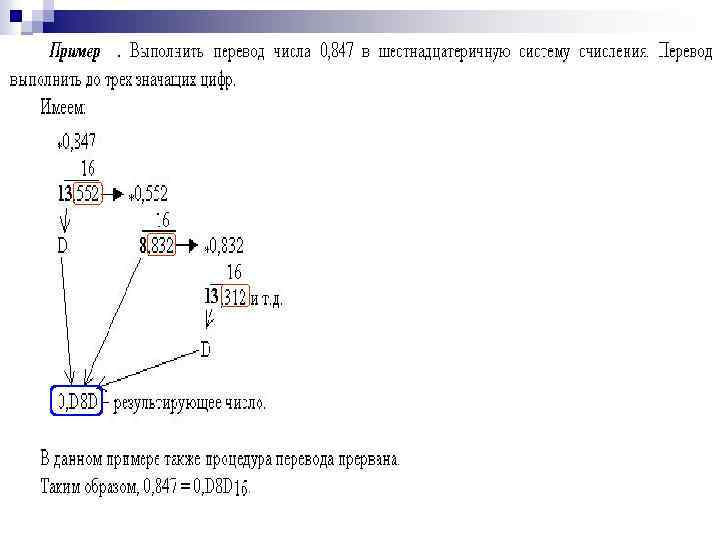
VI. Перевод неправильных дробей из десятичной системы счисления:

VII. Выполнение простейших арифметических действий: 1+1=2=102 1+1+1=3=112

Правила выполнения сложения: 1. Цифры данного числа подписываются строго по разрядам; 2. Число, получившееся при сложении соответствующих цифр (в каждом разряде) переводиться в ту систему счисления, в которой производится вычисление.

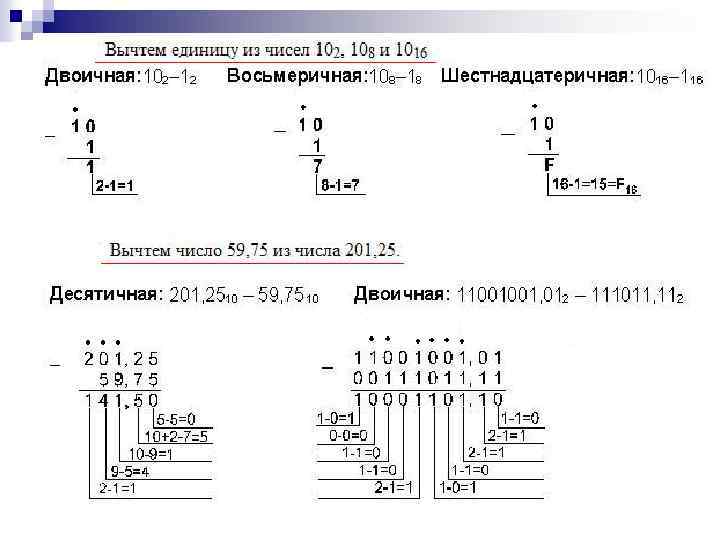
Правила выполнения вычитания: 1. Цифры данного числа подписываются строго по разрядам; 2. Число, получившееся при вычитании соответствующих цифр (в каждом разряде) переводиться в ту систему счисления, в которой производится вычисление; 3. Если уменьшаемое меньше вычитаемого, то производится заём у впереди стоящего разряда; 4. Заём: 2 -ая СС – 2 8 -ая СС – 8 10 -ая СС – 10 16 -ая СС – 16

Умножение и деление в различных системах счисления Умножение. Выполняя умножение многозначных чисел, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо переводить в ту систему счисления в которой выполняется вычисление. 1 строка: ответ 531 2 строка: ответ 1262 При сложении результатов обратите внимание на сумму цифр в третьем столбике (с конца): 6*3=18=228 5+6=11=138 3*3=9 = 118 3*6=18, 18+1=19=238 3*1=3, 3+2=58 6*6=36, 36+2=38=468 6*1=6, 6+4=10=128

Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей.

1) 1335: 163, берём приблизительно по 8 (прикидываем как в 10 -ой СС), но такой цифры в 8 -ой СС нет, поэтому попробуем по 7. 2) 163*7=14458 3) Это больше, чем 1335, поэтому берём по 6. 4) 163*6=12628 5) 2) 1335 -1262=538 , сносим 1 3) 531: 163, берём по 3 4) 163*3=5318

Самостоятельная работа: 1. Перевести данные числа из десятичной системы счисления : 1) 54 → 2, 7) 481, 625 → 8, 2) 159 → 8, 8) 125, 125 → 2, 3) 1018 → 16 9) 18, 5 → 16, 4) 37 → 2, 10) 124, 25 → 2 5) 245 → 8, 11) 43, 78 → 16, 6) 315 → 16

2. Перевести данные числа в десятичную систему счисления. 1) 10001, 01 (2) 2) 174, 2 (8) 3) 0, 803 (16) 4) 7764, 1 (8) 5) 1001, 1 (2) 6) AD, A 8 (16)

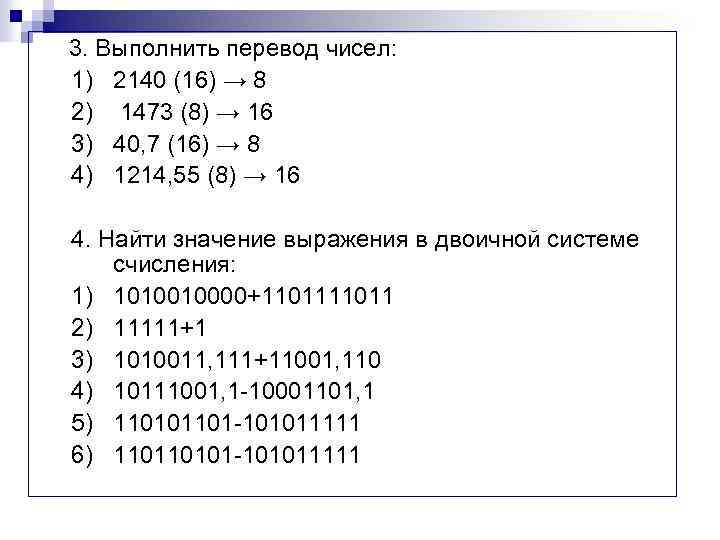3. Выполнить перевод чисел: 1) 2140 (16) → 8 2) 1473 (8) → 16 3) 40, 7 (16) → 8 4) 1214, 55 (8) → 16 4. Найти значение выражения в двоичной системе счисления: 1) 1010010000+11011 2) 11111+1 3) 1010011, 111+11001, 110 4) 10111001, 1 -10001101, 1 5) 110101101 -101011111 6) 110110101 -101011111

5. Вычислить: 1) (11111012 + AF 16 ) : 368 2) 1258 + 111012 * А 216 – 14178 3) 6. Найти среднее арифметическое чисел: 4) 100101102 ; 1100102 5) 7. Вместо звёздочек расставьте знаки «+, -, , : » . Определите самостоятельно в какой системе счисления выполняются действия. 6) 1100*11*100=100000 7) 1100*11*100=0 8) 1100*10*10=100 9) 1100*10*10=110000 10)1100*10*10=1011