Системы счисления Панчева Т Ю

Системы счисления Панчева Т. Ю.

• • Урок 1 Урок 2 Урок 3 Урок 4 Урок 5 Урок 6 Урок 7

Тема: История возникновения и развития систем счисления Система счисления - способ представления числа символами некоторого алфавита, которые называют цифрами.

Десятичная система счисления В этой системе алфавитом служат десять цифр От 0 до 9. Возникновение десятичной системы счисления явилось важнейшим достижением человеческой мысли.

Двенадцатеричная система счисления • Происхождение этой системы связано со счетом на пальцах. Элементы двенадцатеричной системы счисления сохранились в Англии в системе мер, в денежной системе. • (1 фут =12 дюймам. )

Восьмеричная система счисления Шведский король Карл XII в 1717 г. Считал эту систему наиболее удобной и намеревался ввести её как общепринятую.

Двадцатеричная система счисления • Основу для счета в этой системе составляли пальцы рук и ног. • Денежная единица Франции 1 франк=20 су

Шестидесятеричная система счисления • Так называемая «Вавилонская» . Такая система счисления громоздка. Дошла до наших дней. • 1 час=60 минут, • 1 градус=60 ‘ 3/17/2018

• Группы Систем счисления анатомического происхождения: десятичная пятеричная двенадцатеричная двадцатеричная машинные: двоичная восьмеричная шестнадцатеричная алфавитные: славянская древнегрузинская древнеармянская древнегреческая Выход в меню

Урок 2 Тема урока: Классификация систем счисления.

Понятие систем счисления • Система счисленияэто совокупность правил для обозначения и наименование чисел.

Системы счисления делятся на: • Непозиционные системы счисления. • Позиционные системы счисления. • Унарная система счисления.

Непозиционная система счисления • Непозиционная с/с это система в которой количественный эквивалент каждой цифры не зависит от ее положения в коде числа.

Недостатки непозиционной системы счисления • 1)Невозможно записывать дробные и отрицательные числа. • 2)Сложно выполнять арифметические операции. • 3)Для записи больших чисел приходится вводить новые числа.

Унарная система счисления • Унарная с/с - это система для записи любых чисел с использованием символов: • палочки • узелки • зарубки.

Позиционная система счисления. • Позиционная с/с это система где, количественный эквивалент цифры зависит от ее места в коде числа.

Достоинство позиционной системы счисления 1. Простота выполнения арифметических операций. 2. Ограниченное количество символов, необходимых для записи числа.

Пьер Симон Лаплас (1749 – 1827) (французский математик) «Мысль выражать все числа немногими знаками, придавая им, кроме значения по форме, еще значение по месту, настолько проста, что именно из-за этой простоты трудно оценить, насколько она удивительна» .

ВЫВОДЫ • Позиционных систем очень много, так как за основание системы можно принять любое число не меньше 2. • Наименование системы счисления соответствует её основанию ( десятичная, двоичная, пятеричная и т. д. ).

Выполни задание. • Запиши код, месяц и число своего рождения с помощью римских цифр. • Запишите с помощью старинной русской системы счисления число 2357 руб. 53 коп. • Придумайте свою непозиционную систему счисления. Выход в меню

Урок № 3 ТЕМА УРОКА: АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ. ЦЕЛЬ УРОКА: Рассмотреть все арифметические операции в двоичной системе счисления.

ПРАВИЛА ВЫПОЛНЕНИЯ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ НАД ЧИСЛАМИ, ПРЕДСТАВЛЕННЫМИ В ДВОИЧНОЙ СИСТЕМЕ СЧИСЛЕНИЯ:

СЛОЖЕНИЕ: Правила сложения: 0+1=1; 1+0=1; 1+1=10. Т. к. 1+1=10, то 0 остается в данном разряде, а 1 переносится в следующий. ПРИМЕРЫ: 1. 1001+1010=10011 2. 1101+1011=11000

Реши сам. 1. 2. 3. 4. 10010011+101101= 10110111+100110= 110111+111001= 101101+11011=

УМНОЖЕНИЕ: Операция умножения двоичных чисел сводится к умножению множимого на каждый разряд множителя с последующим сдвигом и суммированием полученных произведений, аналогично умножению в десятичной системе. 1101 10000012

ДЕЛЕНИЕ: Выполняется подобно операции деления в десятичной системе: 10101 111 11 111 0

ЗАДАНИЕ РАЗДЕЛИТЕ: 1111: 11= 11100111: 1011= 1111: 101= :

Для самостоятельной работы:

ДОМАШНЕЕ ЗАДАНИЕ: 1. 2. 3. 4. 5. 6. 10101+1101= 1111+11= 101000 -11= 100001 -1001= 10001*101= 11110: 11= Выход в меню

ТЕМА: Перевод целых чисел из одной системы счисления в другую.

Правила перевода целых чисел из одной системы счисления в другую.

Правило № 1 Основание новой системы счисления выразить цифрами исходной системы счисления и все последующие действия производить в исходной системе счисления.

Правило № 2 Последовательно выполнять деление данного числа и получаемых неполных частных на основание новой системы счисления до тех пор , пока не получим неполное частное , меньше делителя.

Правило № 3 Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.

Правило № 4 Составить число в новой системе счисления, записывая его начиная с последнего остатка.

ПРИМЕР Н 10=86 8610 = 10101102 86 43 2 0 42 21 2 1 20 10 2 1 10 5 2 0 4 2 2 1 2 1 0

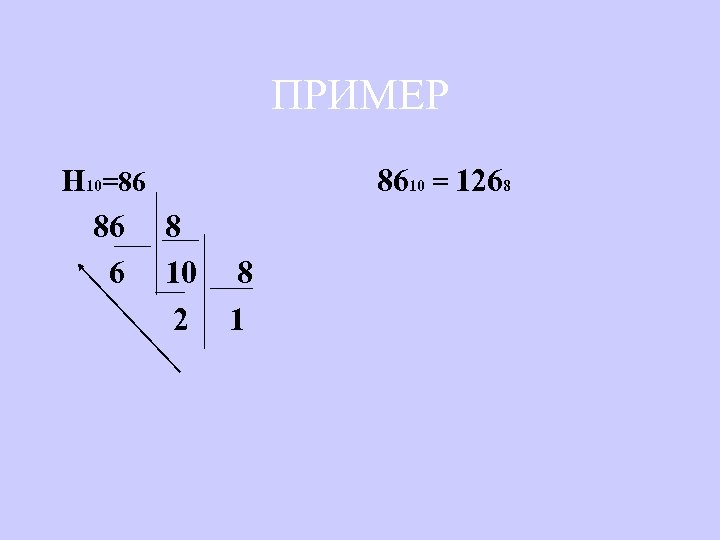ПРИМЕР Н 10=86 8610 = 1268 86 8 6 10 8 2 1

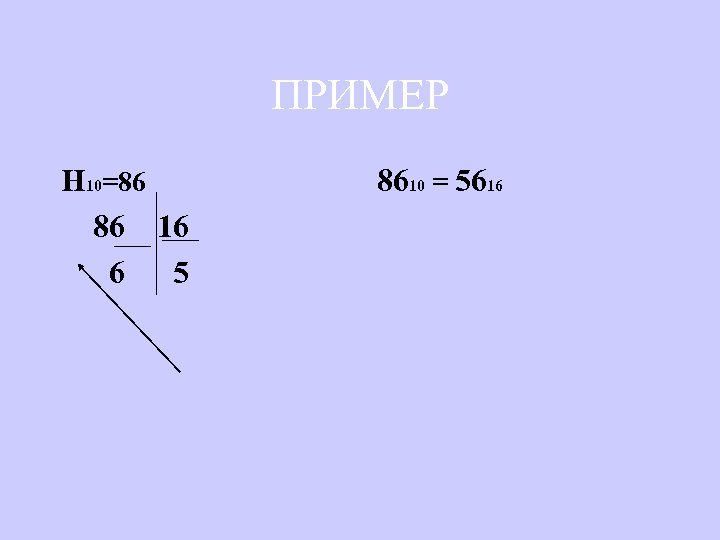ПРИМЕР Н 10=86 8610 = 5616 86 16 6 5

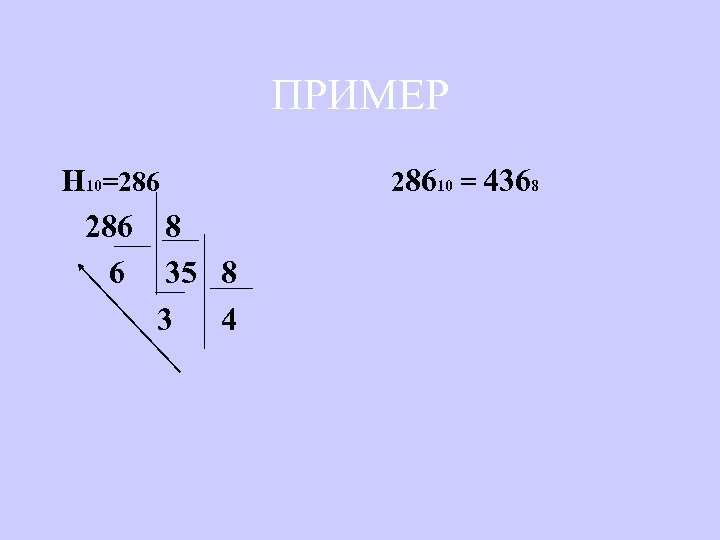ПРИМЕР Н 10=286 28610 = 4368 286 8 6 35 8 3 4

Выполни задание Переведите целые числа в восьмеричную систему счисления. 8700, 8888, 8900, 9300 Переведите целые числа в шестнадцатеричную систему счисления. 266, 1023, 1280, 2041 Выход в меню

ТЕМА УРОКА: ПЕРЕВОД ДРОБНЫХ ЧИСЕЛ ИЗ ОДНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ДРУГУЮ.

Можно сформулировать алгоритм перевода правильной дроби с основанием p в дробь с основанием q :

1. ОСНОВАНИЕ НОВОЙ СИСТЕМЫ СЧИСЛЕНИЯ ВЫРАЗИТЬ ЦИФРАМИ ИСХОДНОЙ СИСТЕМЫ СЧИСЛЕНИЯ И ВСЕ ПОСЛЕДУЮЩИЕ ДЕЙСТВИЯ ПРОИЗВОДИТЬ В ИСХОДНОЙ СИСТЕМЕ СЧИСЛЕНИЯ.

2. ПОСЛЕДОВАТЕЛЬНО УМНОЖАТЬ ДАННОЕ ЧИСЛО И ПОЛУЧАЕМЫЕ ДРОБНЫЕ ЧАСТИ ПРОИЗВЕДЕНИЙ НА ОСНОВАНИЕ НОВОЙ СИСТЕМЫ ДО ТЕХ ПОР, ПОКА ДРОБНАЯ ЧАСТЬ ПРОИЗВЕДЕНИЯ НЕ СТАНЕТ РАВНОЙ 0 ИЛИ НЕ БУДЕТ ДОСТИГНУТА ТРЕБУЕМАЯ ТОЧНОСТЬ ПРЕДСТАВЛЕНИЯ ЧИСЛА.

3. Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы.

4. Составить дробную часть числа в новой системе счисления , начиная с целой части первого произведения.

Рассмотрим примеры. • Пример № 1 • 0, 6562510=0, 528 • 0 65625 • 8 • 5 25000 • 8 • 2 00000 3/17/2018

Пример№ 2 0. 72610=0. В 9 D 16 0 726 16 11 616 16 9 856 16 13 696 … 3/17/2018

Для перевода смешанных чисел. 1. Перевести целую часть. 2. Перевести дробную часть.

Пример 124, 2510=174, 28 124 8 120 15 8 4 8 1 7 0 25 8 2 00

Домашние задания. 1. Перевести число 17, 2510 в двоичную систему счисления. 2. Перевести число 124, 2510 в восьмеричную систему. 3. Перевести число 0, 6562510 в шестнадцатеричную систему счисления. 4. Перевести число 0, 562510 в двоичную систему счисления. Выход в меню

Урок 6 Контрольная работа по теме «Системы счисления»

I вариант 1. Переведите целое десятичное число 91273 в двоичную систему счисления: а) деление на 2 б) по схеме А 10 -А 8 -А 2 в) по схеме А 10 -А 16 -А 2 Проверь правильность полученного результата с помощью обратного перевода в десятичную систему. II вариант 1. Переведите целое десятичное число 100000 в двоичную систему счисления: а) деление на 2 б) по схеме А 10 -А 8 -А 2 в) по схеме А 10 -А 16 -А 2 Проверь правильность полученного результата с помощью обратного перевода в десятичную систему.

I вариант • 2. Переведите правильную дробь 0, 66321 из десятичной системы счисления в двоичную. Ответ запишите с 12 двоичными знаками. • 3. Переведите число из двоичной системы счисления в десятичную. Счет ведите с 4 -мя знаками после точки. II вариант • 2. Переведите правильную дробь 0, 000202 из десятичной системы счисления в двоичную. Ответ запишите с 13 двоичными знаками. • 3. Переведите число 0, 111100110111 из двоичной системы счисления в десятичную. Счет ведите с 4 -мя знаками после точки.

I вариант 4. Выполните арифметические операции в двоичной системе счисления: 111001011+1001001101= 110110100111000100100= 101101*110001= 11000111111: 100111= Выполни проверку полученного результата с помощью обратного перевода в десятичную систему счисления. II вариант 4. Выполните арифметические операции в двоичной системе счисления: 1110001011+1001001101= 110110100111000100100= 101101*110001= 11000111111: 100111= Выполни проверку полученного результата с помощью обратного перевода в десятичную систему счисления. Выход в меню

Тема урока: Перевод из произвольной системы счисления в десятичную систему счисления.

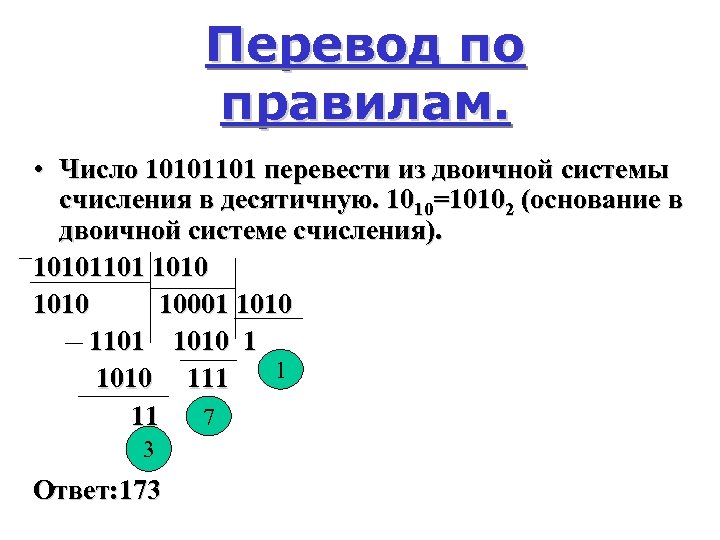Перевод по правилам. • Число 10101101 перевести из двоичной системы счисления в десятичную. 1010=10102 (основание в двоичной системе счисления). 10101101 1010 10001 1010 1101 1010 1 1 1010 111 7 11 3 Ответ: 173

2 способ.

Пример 10101101 перевести из двоичной системы счисления в десятичную. 101011012=1*27+1*25+1*23+1* 2+1*20=173 2 10

3 Способ.

Пример • Перевод целых определяются формулой: • 1101011 • Si=Sj*g+aj Sn=0; A 10=S 0 l=n-1 • S 6=0*2+1=1 • S 4=3*2+0=6 • S 2=13*2+0=26 • S 0=53*2+1=107 Ответ: 10710

Пример. • • Перевод дробных чисел: 0, 1110101 S 7=0: 2+1=1 S 6=1: 2+0=0, 5 S 5=0, 5: 2+1=1, 25 S 4=1, 25: 2+0=0, 625 S 3=0, 625: 2+1=1, 3125 S 2=1, 31: 2+1=1, 65 S 1=1, 65: 2+1=1, 82 S 0=1, 82: 2+0=0, 9140 0, 1110101=0, 9140

Сделай сам! • Перевод целого числа из двоичной системы в десятичную по схеме Горнера. • • 110101110001110 101100100101001101 11000011010100000 Выход в меню

Перевод чисел из систем счисления с основанием 2 n в систему счисления с основаниям 2 и обратною. Если основание q-ичной системы счисления является степенью числа 2, то перевод числа из qичной системы счисления в 2 ичную и обратно можно проводить по более простым правилам.

q=23 дано число (abcdef)2= ax 25+bx 24+cx 23+dx 22+ex 21+fx 20 =(ax 22+bx 21+cx 20) х 23 + (d x 22 +e x 21 +f x 20) =A x 23 + B = A x 8 + B A 8= ax 22+bx 21+cx 20= abc 2 B 8= d x 22 +e x 21 +f x 20= def 2

Перевод целых чисел. Алгоритм перевода целых двоичных чисел в систему с основанием g=2 n

• • • Данное двоичное число разбить справа налево на группы по n цифр в каждой. Если в последней левой группе окажется меньше n разрядов, то её надо дополнить слева нулями до нужного числа разрядов Рассмотреть каждую группу как n-разрядное двоичное число и записать её соответствующей цифрой в системе счисления с основанием g=2 n

• Пример. Перевести число в восьмеричную систему счисления. 10110000110010 Разбиваем число на триады. 101 100 001 000 110 010 5 4 1 0 6 2 5410628 = 101100001100102

Пример • Перевести число 1000001111100001112 в шестнадцатеричную систему счисления. 0010 0000 1111 1000 0111 2 0 F 8 7 200 f 87 16 = 1000001111100001112

Перевод дробных чисел. • Данное двоичное число разбить слева направо на группы по n цифр в каждой. • Если в последней правой группе окажется меньше n разрядов, то её надо дополнить справа нулями до нужного числа разрядов • Рассмотреть каждую группу как nразрядное двоичное число и записать её соответствующей цифрой в системе счисления с основанием g=2 n

Пример • Перевести число 0, 100000112 в шестнадцатеричную систему счисления. 0000, 1000 0011 0 , 8 0 3 0, 803 16 = 0, 100000112

Пример • Перевести число 0, 101100012 в восьмеричную систему счисления. 0000, 101 100 0, 5 4 0, 5428 = 0, 101100012 010 2

Перевести двоичное число в восьмеричную систему счисления

Перевести двоичное число в шестнадцатеричную систему счисления

Попробуй сам Перевести в восьмеричную с/с 111100101 Перевести в шестнадцатеричную с/с 0, 110100102 Перевести в двоичную с/с. 4 АС 3516 Выход в меню